基于博弈论的EPC项目评标方法研究

2022-06-23韦春昌聂春龙李佩琪石爽

项目管理技术 2022年6期

韦春昌聂春龙李佩琪石爽

(南华大学，湖南衡阳 421001)

0 引言

招投标法[1]是我国当前工程项目选择总承包商普遍采用的方法。在招标过程中，采用的评标方法却相对较粗糙，缺乏相应的理论依据和科学指导，多数运用综合评标法和最低价中标法。然而评标方法是否科学合理，直接关乎整个招标活动的成功与否，意义重大。我国招投标起步相对较晚，在实际招标过程中仍存在诸多挑战，尤其是在评标方法的理论上缺乏深入的研究，实践方面也欠缺相关经验。对此，建立科学、合理、实用的评标模型具有重要的理论指导意义。综合评标法受主观因素的影响，评标委员和专家的主观性对评标结果具有较大的偏向性，同时还涉及腐败的滋生，另外在评标的价格和技术以及商务的权重确定上缺乏科学性。合理低价评标法在价格上有一定的对比性，但缺乏对工程技术和质量的审查，低价中标会造成投标商只比价格不比质量技术，唯价格论，引发“劣币驱逐良币”等现象。正确建立并分析评标过程中的相关因素，运用科学合理的评标方法模型，营造一个公平竞争的良好环境，将有利于业主最终择优选出最佳的总承包商。

1 EPC项目评标方法

EPC[2]是施工项目的总承包模式，具有固定总价、项目的综合管理以及合理工期等优点，是当前大中型建设工程项目的主要承包模式。这个模式有效克服了设计、采购和施工等几方承包商之间的相互制约问题，减少了业主对项目资金、人力投入的浪费，从而有效地控制了施工项目的建设质量、成本和进度，提高了项目投资的经济效益。通过招投标活动选择一个优秀的项目总承包商对于项目的开展和完成都至关重要。因此，评标是招标活动中最重要的一环，合理分析和设置评标因素，采取科学客观的评标办法，选出更优秀、更合适的总承包商，对保证工程施工的质量和项目综合经济投资效益，营造一个良好的招投标市场环境具有重要作用。

本文对EPC项目评标的研究建立在分析综合评标法的基础上。针对综合评标法评标过程中存在的模糊性和仅靠专家主观判断带来的偏差性问题，重新构建了评标指标体系，并提出基于G1-熵权-博弈论法确定评标指标权重，利用博弈论组合赋权[3-4]技术使主客观赋权相结合，克服人为的主观性及客观的片面性。结合评标现场专家评分值，选出更优秀的投标单位；提高评标的科学准确性，为评标活动提供一定的科学指导。

2 评标指标体系

在借鉴现行国家标准和规范的基础上，通过阅读大量资料文献，再结合工程项目的情况，邀请相关专家开展头脑风暴，对评标指标进行筛选确定，并考虑层次性，从项目管理机构评审、技术方案评审、投标报价以及其他因素4个维度建立EPC项目的评标指标体系。评标内容在4个维度的基础上，参考现场述标的结构和完整性、答辩时对项目的熟悉了解程度、技术标的专业性和技术性、应对特殊日期及疫情影响对项目的响应方案和抢工措施、安全质量管理、劳动力安置和现场协调问题、物料储存周转及报价、业绩等诸多方面，归纳总结出方案层指标，其评标指标体系见表1。

表1 评标指标体系

3 项目评标模型的建立

3.1 G1法确定主观权重

通过查阅文献，目前对指标权重确定的方法主要有集对分析法、德尔菲法和G1法、层次分析法、网络层次分析法等[5-6]。EPC项目评标指标的层次性以及每个指标受诸多因素的影响，定性指标居多，另外项目的差异也会造成指标权重的差异，所以运用G1法更适合确定EPC项目评标指标的权重。此方法是对层次分析法加以改进，利用层次性对指标的重要程度进行排序，根据排序后的序关系计算指标的权重。方法简便直观，减少了特征值的计算和一致性的检验，减少了计算的冗余。其具体步骤如下：

rk=xk-1/xk

(1)

表2 rk赋值说明表

(2)计算权重系数wn，即

(2)

则其余n-1个指标的权重为

wk-1=rkwk

(k=n,n-1,…,3,2)

(3)

3.2 熵权法确定客观权重

指标权重结合熵权法计算，能克服主观确定指标权重的不确定性。对n个对象m个评价指标打分，得到原始矩阵Y=(yij)(i=1,2，…，m；j=1,2，…，n)。yij为第j个指标下第i个指标的评价值。

根据熵的定义，评价指标熵值计算为

(4)

其中

熵值权重为

(5)

3.3 基于博弈论确定指标的组合权重

G1法和熵权法都存在局限性，利用博弈论，对主客观权重进行组合赋权。根据博弈论法，把主观、客观看作博弈的双方，双方博弈达成的妥协或者一致性即是最优组合权重。在这种状态下，应满足主观权重和客观权重与指标组合权重之间的离差之和最小。博弈论思想组合赋权的具体步骤如下：

利用L种赋权方法分别对n个评标指标赋权，可得权重Wk=(wk1,wk2,…,wkn)，其中k=1,2,…,L。

权重的线性组合为

(6)

博弈论的集结模型主要是一个多人优化的问题，博弈双方达到的平衡即是对式(5)中L个线性组合系数的最大优化，使得W和各个Wk之间的离差最小化，可导出式(7)模型为

(7)

据矩阵的微分原理，由式(7)得到等价线性方程为

(8)

求解得出博弈后的最优线性组合系数为λ*=[λ1，λ2，…，λL]

并进行归一化处理

(9)

计算博弈后的最终权重为

(10)

(k=1,2,…，L)

4 实例论证

本文选取长沙智慧产业城总部大楼施工总承包项目的招标评审进行实例论证。项目位于湖南省长沙市，招标项目已完成项目开项、立项，已具备招标条件。本次总部大楼项目招标规模为地下1层、地上8层，建筑面积约24万，采用框架-剪力墙结构，大跨度、大悬挑部分采用钢桁架结构。招标范围包括土石方工程、地基基础工程、主体结构工程、钢结构工程及消防工程等的材料和设备采购、施工、验收、交付以及BIM技术应用等。邀请了7名评标专家，根据本文建立的评标指标体系，先从技术、管理、商务等因素入手，结合现场述标答辩情况，综合对各个指标进行评标打分，然后结合确定的权重，计算综合得分，最终确定中标单位。

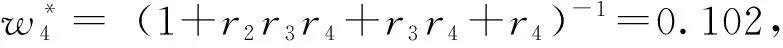
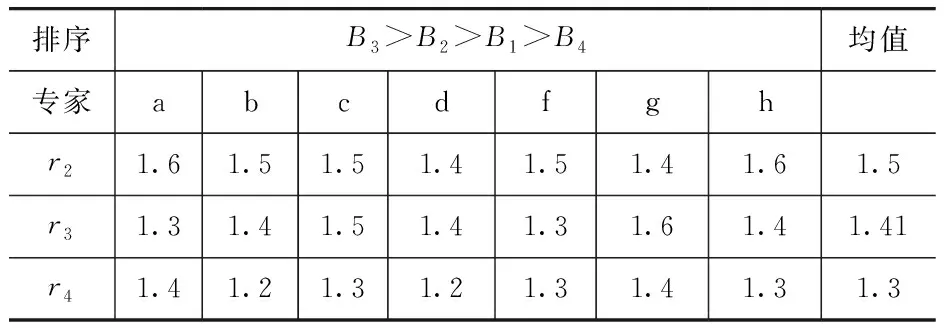
表3 准则层排序及重要度赋值

根据重要程度序列得到指标层权重

w=(0.190,0.307,0.401,0.102)

同理可得，方案层权重

w1=(0.059,0.087,0.044)

w2=(0.072,0.078,0.060,0.051,0.045)

w3=(0.242,0.159)

w4=(0.028,0.040,0.034)

由熵权法计算指标权重时，结合类似项目数据的投标报价比和各投标人因素，根据指标的定性和定量结合方式，同时参照专家评分，由式(4)、式(5)得到指标层权重

w′=(0.181,0.295,0.432,0.092)

方案层权重

w′1=(0.060,0.070,0.051)

w′2=(0.080,0.089,0.060,0.038,0.027)

w′3=(0.295,0.137)

w′4=(0.021,0.037,0.035)

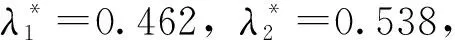
W=(0.185,0.301,0.417,0.098)

同理得方案层权重

W1=(0.059,0.079,0.047)

W2=(0.080,0.092,0.07,0.031,0.028)

W3=(0.269,0.148)

W4=(0.024,0.038,0.036)

根据项目投标报名情况并结合项目本身特点，邀请20家资质能力较强的单位投标，对最终按要求如期提交标书的6家(A～F)参与投标的单位进入现场开标。根据开标现场提交的标书，结合现场述标答辩情况，由评标委员进行评标打分，各项评分细则依据招标文件评审标准，投标报价评审计分最终以报价和基准价按表4的原则计算。

表4 投标报价评审计分原则

评标专家根据公平公正原则，对评标指标进行评分，各项评分细则严格依据招标文件执行，最后汇总整理得到7名专家的各个评标指标的平均分值，见表5。

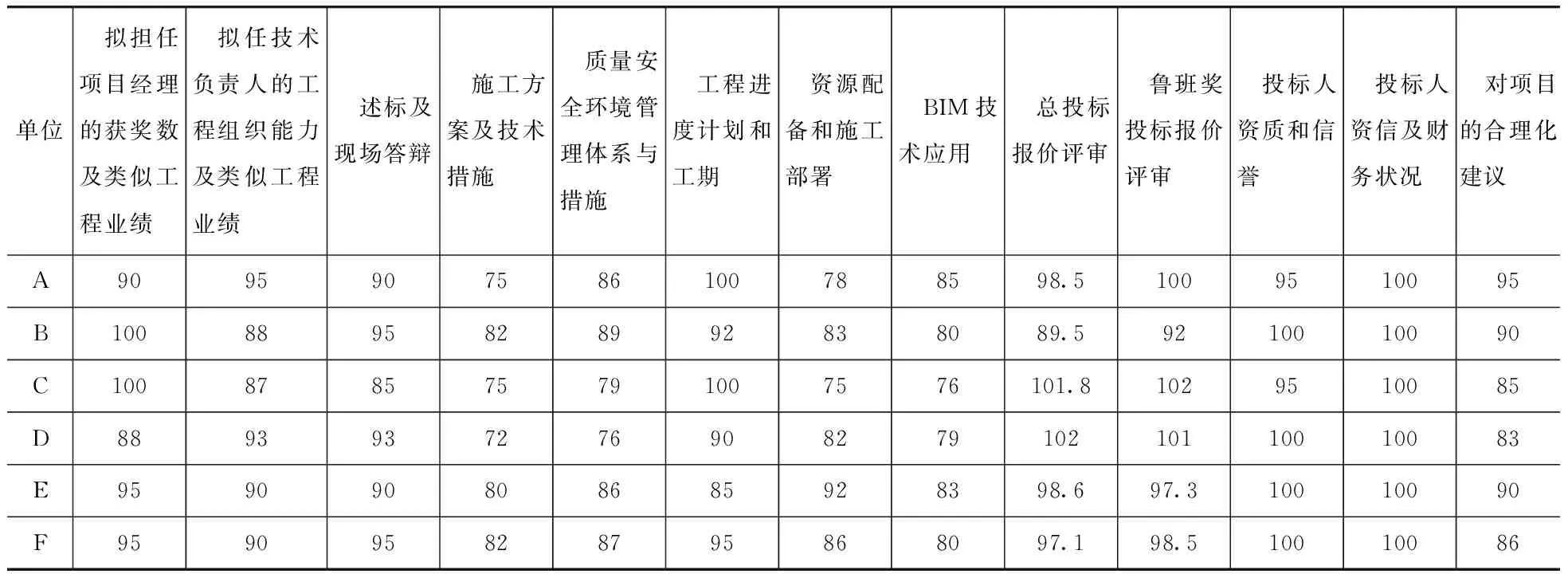
表5 指标评分表

用重新构建的指标体系权重，与对应指标的评标分值的乘积，最后求总评标得分，得出6家投标单位的评标分值为93.55，90.45，93.10，92.29，92.74，93.29。根据分值最高的中标原则，确定投标单位A为中标第一候选人，投标单位F为中标第二候选人。

由上述确定的权重结合评分计算方法可以看出，采用G1法、熵权法和博弈论确定的组合权重得出的结论，和直接打分法在评标中得出的结果存在差异。直接打分法在评定中标单位过程中A，E，F的得分接近，难以直接分出优劣。基于博弈论研讨后能够更直观地选出更具竞争优势的投标单位。在评标中，降低投标报价的指标权重，增加其在技术标和项目管理方面的比重，降低低价中标的概率，减少建筑业里“只比价格不比质量技术”和唯价格论的现象，同时降低招标底价泄露的可能性。在技术标和项目管理方面，针对开标、述标和答辩，结合投标单位对施工组织安排、智慧工地的综合考虑、现场生活区办公区和物料周转区及设备的布置、工期、质量安全环境等方面的综合评标，另外加入对项目的合理化建议，以提高对项目其他方面的考虑和理解。