基于知识“临界点”培养数学结构化思维

2022-06-21林平芬福建省龙岩市莲东小学

基础教育论坛 2022年9期

林平芬（福建省龙岩市莲东小学）

“临界点”是物理学名词，指物体由一种状态变成另一种状态前，应具备的条件。例如：水→冰→水蒸气，因为能量不同而出现了相的改变，相的改变代表界的不同，这时，我们称它为临界了，而临界时的值则称为临界点，后来人们用以形容事态发展的待变状态。那么，我常想：在数学中，是否存在待变状态，也就是“临界点”呢？《基于核心素养的小学数学结构化思维培养》课题开展研究后，我发现“临界点”在数学知识体系中不仅无处不在，还蕴含着丰富内涵，具有特殊性，只不过在教学中往往被忽略而已。

多年的教学实践中，我从“临界点”出发，引导学生去认识它，寻找它，理解它，运用它，从而引导学生逐步走向结构化思维的探索之路。

一、认识“界”，感受“界”之特殊

何为数学知识领域里的“临界点”呢？我以下列说明：

张奠宙先生说：“首先要给出0，再谈正负数。”把这句话转化为数学符号语言：正数→0→负数，以“0”为界，就形成了一个数域的结构，如果放到数轴上，结构就一目了然了。（如图一）

图一

以“0”为界，形成数域结构后，我们再来解读教材就更能理解编者的设计意图了。人教版六年级下册“认识负数”这单元，共有3个例题，例1以温度引入课题，0°C表示淡水开始结冰的温度，是零上温度与零下温度的分界点，这是自然意义规定的相反量；还有一种人为规定的分界，如教材中的例2、例3：例2从存折分析，收入为正，支出为负；例3以大树为界，向东为正，向西为负；除此以外，如，以海平面为界（记作0），比海平面高记为正数，比海平面低记为负数；以商场为例，盈利为正、亏损为负；以产品质量标准如薯片200克为界（记作0），超出部分为正，不足部分为负，以北京时间为界（记作0），比它早为正，比它迟记为负……但无论是自然规定还是人为规定，正负数的分界点为0是无可厚非的。自然意义规定的“0”（如气温），学生是有体验的，固定的、比较容易理解；而人为规定的“0”是变化的，学生的体验不足，难度就增加了。但如果明确了“0”这个分界点的重要性，确定了0，再来谈正负数，难度就降低了。

这样，学生就能较好地认识“界”的真正内涵，并感受其特殊必性，从而形成数域结构，促进结构化思维的形成。

二、寻找“界”，发现“界”之所在

学生认识了“界”之后，在学习过程中，我们应该引导学生寻找更多的“临界点”，并自主建构各种数学知识结构体系，努力促进学生结构化思维的形成。我是从以下三方面引领学生寻找“临界点”的：

（一）从特殊点入手寻找

“特殊点”之所以特殊，就在于它的与众不同。如“0”。我们知道，以“0”为界，可以区分正负，以“0”为界，点上“小数点”，还能把一个小数分成了整数部分、小数点和小数部分。0就是一个特殊点；还有“1”，以“1”为界，可以区分真假分数，比1大的分数，即分子比分母小的分数叫作真分数，比1大或等于1的分数，即分子比分母大或分子与分母相等的分数叫作假分数。以“1”为界，一个数，乘1，就得原数；一个数乘比1大的数，积就比原数大；一个数乘比1小的数，积就比原数小。同理，以“1”为界，一个数除以1，除以比1大的数、除以比1小的数，商也有一定的规律。以90°为界，可以对角进行分类：小于90°的是锐角、等于90°的是直角，大于90°小于180°的是钝角，等于180度的是平角，等于360°的是周角，大于180°而小于360°的是优角……像这样，数学知识领域里的特殊点比比皆是，在日常的数学学习中，我们如果能引导学生随时关注各种“临界点”，并迅速建立起各种知识结构，便能很好地掌握数学知识的本质特征，培养学生的结构化思维能力。

（二）从对比入手寻找

“临界点”的核心特征是“相变”，那么，教师就应该引导学生观察“相变”的过程，并对变化前后的数量关系、空间形式进行对比，便可寻找到“临界点”之所在。“十进制”计数法是目前世界通用的计数法，1，2，3，4，5，6，7，8，9，当数到9时，再添上1就是10，数的表征从一位数变成了两位数，即数由一个数字转变为两个数字组合而成。“10”就是一位数变为两位数的分界点，这个特殊性如何引导学生发现并感知呢？教材里用数小棒的活动，1根、2根、…9根，当数到9根时，再添上一根是10根，把它们捆成一捆，课堂教学实践中，教师需要引导学生思考：“为什么要捆成一捆呢？”“这一捆小棒可以表示什么？还可以表示什么呢？”学生操作时，10根“捆”成一捆的操作就赋予了“1个十”和“10个一”的含义，数出10根，捆成一捆，再拆开来，数一数，再捆成一捆，这样反复操作，引导学生充分感知10个一等于1个十，1个十等于10个一，建构了“十进制”计数法的模型，为后续十位上的满十进一、百位上的满十进一、千位上的满十进一……提供了有力的经验，学生自然就能迁移应用。从“10”这个特殊的数字出发，感受十进制的进位“临界点”的特殊性，是对后续学习“数与代数”领域知识具有深远影响的关键生长点。

（三）从运动入手寻找

在《三角形》单元教学中，我在学生认识三角形并学会了分类后，设计了运用几何画板，让学生在方格图中通过运动，感受三角形顶点平移引起角的大小变化、引起三角形分类的变化、引起三角形高的位置的改变的探究。以直角形为界，我先固定了一个锐角三角形和一个直角三角形，再让钝角三角形随着顶点D运动起来，截图如下（图二）：

图二

当钝角三角形的顶点D平移运动起来后，我提出了三个问题：

钝角三角形的顶点D平移运动时，什么变了，什么不变？

什么时候会变成直角三角形呢？以直角三角形为界，当点D走到哪儿时，变成锐角三角形？走到哪儿时又变成了钝角三角形呢？

你还有什么发现吗？

在讨论第1个问题时，有的学生认为钝角三角形的顶点D平移运动时，三角形的底边不变，顶点D的位置变了，另外两条边的位置与大小随之改变，所以三角形的角度、形状都变了，有时是钝角三角形，有时是直角三角形，有时是锐角三角形。

在讨论第2个问题时，有的学生直观指出，当三角形的高DB与边DC重合时，就是直角三角形，只有这两种情况。

当点D在底边BC的正上方之间时，也就是高在三角形内，是锐角三角形；当D点移到线段BC的上方外时，这个三角形就变成了钝角三角形。

在讨论第3个问题“你还有什么发现？”时，学生说，在方格图里，我可以清楚看见三角形的底不变，高的长度也不变，形状不断变化。

运用几何画板让图形运动起来，或旋转，或平移，以问题驱动学生观察、思考、分析，让学生能直观地看明白，以直角三角形的直角边为界，顶点处在不同的位置，三角形的类型就不同，特别是钝角三角形，顶点离底边越远，高就离底边越远，钝角就越大，形状变化就越大，同时，学生经历了“三角形等积变形”的形成过程，明确了直角三角形是形变的“临界点”之所在，从而便自主地建构起知识结构，培养了学生的结构化思维。

像这样在运动中寻找“临界点”的方法，在“图形与几何”领域的教学中常常适用。如：两条直线在同一平面内的位置关系：相交与垂直，运用几何画板，在运动中可以使学生深度理解，在同一平面内，垂直是两条直线相交的一种特殊情况，以它为界，其余的相交都不会成直角，只能称为相交；角的分类也可以，在运动中，以直角为“临界点”，可以迅速帮助学生建立角的类别知识结构。像这样的例子还有很多，在运动国寻找“临界点”，不仅可以帮助学生建构“图形与几何”领域的知识结构，更有利于培养学生的空间观念。

三、理解界，明晰界之关联

建立了界以后，理解界之关联是需要老师下大功夫的。如何理解界之关联呢？数形结合与问题驱动乃是良策。

（一）以表助解，界中晰联

数学家华罗庚说：“数形结合百般好，隔离分家万事休。”无论是“数与代数”领域，还是“图形与几何”领域，均可应用数形结合思想，用画图、列表等方式，帮助学生理解“临界点”，明确界之关联。

以人教版五年级上册“质数与合数”为例：质数的概念是一个数，如果只有1和它本身两个因数，这样的数就叫作质数；合数的概念是一个数，如果除了1和它本身还有别的因数，这样的数叫作合数。那么根据这两个概念，一个数所含的因数数量是判断一个数是质数还是合数的要点，它们的分界点就在2个因数上。为了方便理解，我们可以做成下面的表格（如图三）：

图三

通过上面的列表分析，可以清晰地看出整数1为什么既不是质数，也不是合数，因为它的因数数量最特别，只有1个。而质数是两个，合数的因数数量是2个以上，即3个、4个、5个……通过列表，可以使学生更为清晰地理解质数与合数的界在何处，是怎样建立的，这样的方式形成的数的分类结构是有框架的，有源可溯，有据可依的，用这样的方式建立的概念模型是关联的，牢不可破的。

（二）以形助解，融中建联

除了列表之外，数形结合的强大力量是人尽皆知的，我们要想尽办法，将它融入课堂教学中。以人教版四年级上册“角的度量”为例，我画出这样一条线段（如图四）：

图四

你认为上图中的（）点可能是（）角，大约是（）°，理由是：（）。

这样的设计，把角的分类知识放到线段上，在0o~360o之间，设置不同的点，将数与形结合，引导学生说理，培养学生的数感与量感，渗透了数形结合、化曲为直的数学思想。其中B点表示的约是90°，是直角，它是一个“分界点”，具有参照作用。

理解界，以列表、数形结合等方式分析“界”与“界”之间的关联，明确“界”形成的原因，有助于结构的形成，促进学生结构化思维的培养。

四、运用“界”，实施“界”之本质

学生建立起“临界点”的概念后，就需要有意识地引导他们运用这一知识本质特征去解决问题。如在《三角形》单元教学中，学生运用几何画板建立了“三角形的等积变形”模型后，明确了三角形分类的“临界点”后，我设计了这样一道选择题：

如右图（图五），平行四边形内有一个三角形ABC，已知它的面积是18平方分米，那么阴影部分的面积是（）平方分米。

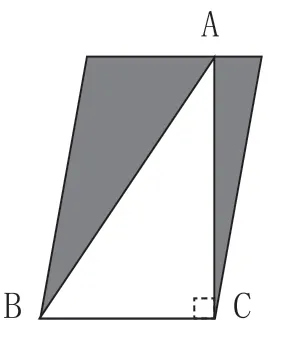
图五

此题只给了一个信息：三角形的面积是18平方分米，要求的是阴影部分的面积是多少平方分米？而阴影部分是由两个三角形组成的，它们的底和高的大小均未知，所以感觉本题有一定的难度。但在我执教的《三角形面积的再认识》一课中，因为学生在图形的“运动”中建立了关于“临界点”的知识结构，有近60%的学生马上给出了答案为C。他们的想法如图六所示，将三角形ABC的顶点A沿着平行四边形的上边平移，移至对角的位置，这时三角形ABC的面积就是平行四边形的一半，也与原来的面积相等（同底等高），所以阴影部分的面积就是三角形ABC的面积。