改头换面 变出精彩
2022-06-21文/陈建
文/陈 建

相信同学们平时做题时都有这样一种感觉,总有做不完的题目和层出不穷的方法。可是,你知道许多问题都是教材例题或习题“改头换面”后出现的吗?下面,我们做个尝试,看看“改头换面”的问题你能否看出来。
一、原题呈现
(苏科版数学教材八年级下册第91 页复习题4)如图1,△ABC和△ADE都是顶角为45°的等腰三角形,BC、DE分别是这两个等腰三角形的底边。图中的△ACE可以看成由哪个三角形通过怎样的旋转得到的?证明△ACE与这个三角形全等。
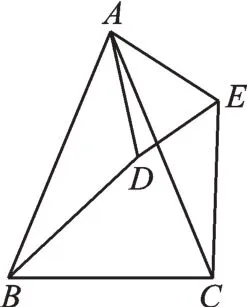
图1
根据条件,同学们不难发现AB、AD分别绕点A逆时针旋转45°可得AC、AE,所以△ACE可以看成由△ABD绕点A按逆时针方向旋转45°得到。条件又告诉我们∠BAC=∠DAE=45°,所以∠BAD=∠CAE,再根据“SAS”就可证得△ABD≌△ACE了。下面,我们对这个问题“改头换面”。
二、改头换面
变式1如图2,若把原题中两个等腰三角形的顶角45°改为90°,请问BD与CE有什么关系?请说明理由。
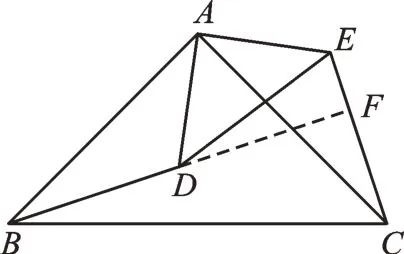
图2
【思路】眼尖的同学已经看出来了,这里仅仅改变了顶角的度数,将“证明三角形全等”改为“探究一组边的关系”。
线段BD与CE的数量关系为BD=CE。变式后的问题证明方法有变化吗?没有变化!其实,两个等腰三形的顶角是45°还是90°无关紧要,我们主要是用其“相等”的特点,证明方法不变。由原题的思路易得△ABD≌△ACE,由此可见BD=CE,∠ABD=∠ACE。再来看看BD与CE的位置关系,延长BD交CE于点F,由∠ABC+∠ACB=90°,可 得∠FBC+∠ACE+∠ACB=90°,即∠BFC=90°。由此可见BD与CE的关系不仅有BD=CE,还有BD⊥CE。
【点评】线段关系一般要从“数量关系”和“位置关系”两个角度思考。
变式2在原题的条件下,连接CD,把△ADE绕点A旋转至DE⊥AC的位置时(如图3),试证明BD=CD。
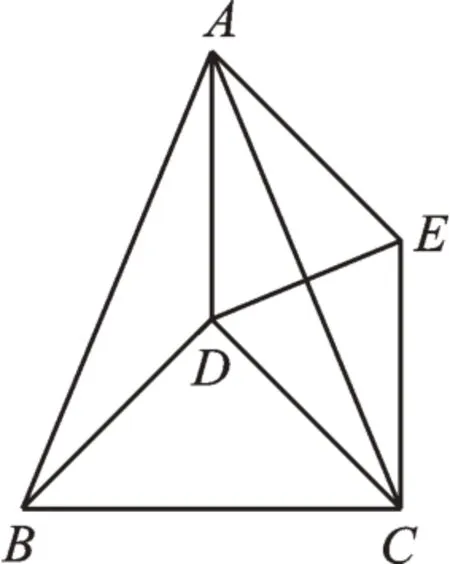
图3
【思路】由于旋转时△ABD和△ACE始终保持全等,故BD=CE。要证明BD=CD,只要说明CD=CE即可。当DE⊥AC且垂足在线段AC上时,由AD=AE,根据“三线合一”可得AC垂直平分DE,所以有CD=CE,从而得BD=CD。当DE⊥AC且垂足在CA延长线上时,同理可得CD=CE。
【点评】给出DE⊥AC这一条件,意味着图形的相互位置关系被部分“锁定”。原来不确定的元素被部分确定,图形必然出现更特殊的性质,探究时要充分利用这些特殊性质。
变式3如图4,把两个等腰三角形的顶角45°改为90°,且AB=AC=2 10,AD=AE=2 2,把△ADE绕点A进行旋转,DE与线段AC相交于点F,当B、D、E三点共线时,求CE的长。
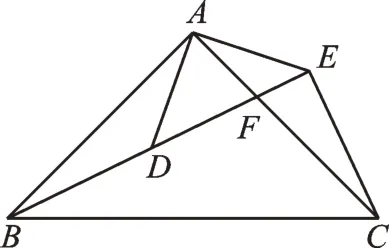
图4
【思路】从条件看,该图形的位置与大小均被“锁定”。由∠ADE=∠AED=45°得∠ADB=135°。根据勾股定理,得DE=4,BC=4 5。由△ABD≌△ACE,可得∠AEC=∠ADB=135°,BD=CE,所以∠BEC=90°。在Rt△EBC中,BC=4 5,BE与EC的差为4,设CE=x,根据勾股定理,有x2+(x+4)2=(4 5)2,解得x=4,即CE的长为4。
【点评】勾股定理是求线段长常用的方法。如果所求线段不在同一直角三角形中,我们应选择条件较多的直角三角形,或设法将分散的条件集中到同一直角三角形之中。
变式4在变式3 的条件下,将“DE与线段AC相交于点F”改为“DE与直线AC相交于点F”,当B、D、E三点共线时,求CE的长。
【思路】DE与直线AC相交,旋转时点F可能在线段AC上,也有可能在线段CA的延长线上。当点F在线段AC上时,思路见变式3。当点F在线段CA延长线上时,如图5,由△ABD≌△ACE,可得∠AEC=∠ADB=45°,CE=BD,又∠AEB=135°,所以有∠BEC=90°。设CE=x,根据勾股定理,有x2+(x-4)2=(4 5)2,解得x=8。所以CE的长为4或8。
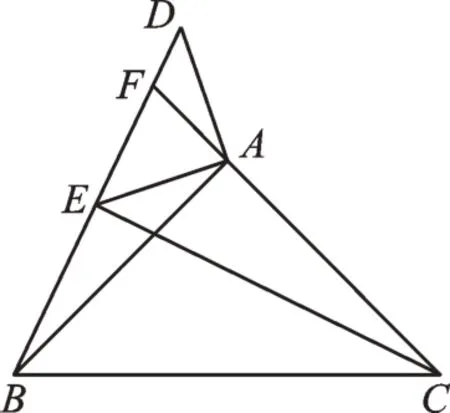
图5
【点评】在解决动点问题时,如果涉及与直线、射线相交的情况,一般要分类讨论,考虑一题多解。若问题没有给出完整图形,则需要自己尝试作图后思考解决。
同学们,通过上面变式问题的分析,你有什么新的收获与启示呢?许多数学变式问题是“形变而神不变”。同学们解题时要透过“变化”的表象看到“不变”的本质,达到“穿上马甲也能认出”的境界。
