图的ISI-Estrada指数的界
2022-06-18李海毓高玉斌
李海毓,高玉斌
(中北大学 理学院, 太原 030051)
0 引言
拓扑指数是一种基于化合物分子图构建的分子描述符,在数学与化学中有着广泛的应用。为了描述小分子和大分子的三维结构,Estrada[1]提出了一种新的基于特征值的拓扑指数,称为Estrada指数。Estrada指数在生物、分子化学、复杂网络等方面都有广泛的应用,是一种重要的分子拓扑指数,相关研究成果可参见文献[2-7]。
设G是一个无环、无重边的简单无向图,其顶点集为V(G)={v1,v2,…,vn},边集为E(G),且|E(G)|=m。若vi与vj相邻, 记为vivj∈E(G),用di表示顶点vi的度。矩阵的零度是指其零特征值的个数,用n0表示矩阵的零度。矩阵的谱半径是指矩阵的特征值中绝对值最大的特征值,而图的谱是指其邻接矩阵G的所有特征值的集合。设A(G)的特征值为λi(i=1,2,…,n),不妨设λ1≥λ2≥…≥λn,则图G的能量[7]被定义为:
图G的Estrada指数[1]被定义为:
基于上述指数,Zangi等[9]定义了n阶连通图G的ISI矩阵AISI=AISI(G),其(i,j)元素为

设ξ1≥ξ2≥…≥ξn为ISI矩阵AISI(G)的特征值,称ξ1为图G的ISI谱半径。图G的ISI能量[8]定义为:
图G的ISI-Estrada指数[10]定义为:

对于文中部分符号和术语,见参考文献[10-11]。
1 ISI-Estrada指数的基本性质
由ISI-Estrada指数的定义,可以得到以下结论:
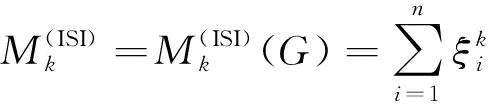
(1)
由图的ISI矩阵的定义可知,对于任意的边vivj∈E(G),则它的权值aij为
(2)
故图G的第k阶ISI谱矩等于图G的每一个k长自回路中边的权值的乘积的和,即
(3)
其中,Ct(G)(3≤t≤n)表示图G中长为t的圈的集合。
结论2设Δ=Δ(G)与δ=δ(G)分别为图G的最大度与最小度,则
1) 对于任意的vi∈V(G),有
1≤δ≤di≤Δ≤n-1
2) 对于任意的vivj∈E(G),根据di,dj≥1
di(dj-1)+dj(di-1)≥0
则

(4)
3) 通过基本不等式,对于任意的vivj∈E(G),有
(5)
结论3由于二部图的ISI矩阵是对称的,故其特征值满足ξn-i+1=-ξi,i=1,2,…,n。因此,若图G为二部图,n0为图G所对应的ISI矩阵的零度,则
(6)

引理1设G为n个顶点的简单图,ξi(i=1,2,…,n)为ISI矩阵AISI(G)的特征值,则
(7)
当且仅当图G为二部图时等号成立。
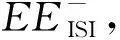


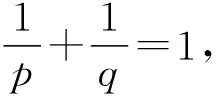
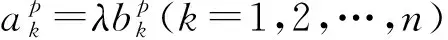
引理3完全二部图Kp,q的ISI矩阵特征值为
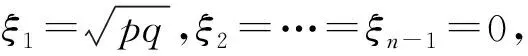
2 图的ISI-Estrada指数的界
利用ISI-Estrada指数的基本性质,根据顶点数和边数、零度等图的不变量给出关于图的ISI-Estrada指数的上下界。
定理1设G为n个顶点m条边的简单图,则
(8)
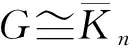
证明先证上界。由式(1)可知


(9)
即
(10)
再证下界。由ISI-Estrada指数的定义可以得到

(11)
利用算数几何不等式,有
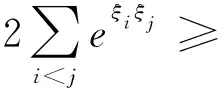
(12)
(13)
其中aij为图G中的边γ∈[0,8]的权值。为了取得更好的下界,设乘数γ∈[0,8],则有
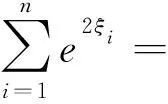
(14)
即
(15)
将式(15)和式(12)代入式(10)可以得到
则

(16)
设函数
因为f(x)在区间[0,8]上单调递减,故当γ=0时f(x)取得最大值,此时EEISI取得最优下界,即

定理2设G为n个顶点、m条边的简单图,r3为G中圈长为3的圈的个数,则
(17)
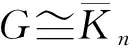
证明根据式(13),利用第二阶、第三阶ISI谱矩展开,则
利用与定理1中同样的方法,设乘数γ∈[0,16],则可以得到
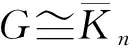
定理3设图G为n阶简单图,k0(≥2)是一个整数,则
(18)
证明采用与定理1、定理2同样的方法,按第k阶ISI谱矩展开可以得到上述定理。
当k0=2时,式(18)为定理1的下界,k0=3时为定理2。
定理4设图G是具有n个顶点、m条边的简单图,且整数k≥2,则
(19)
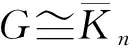
证明由ISI-Estrada指数的定义有
则


在上述定理中,令k0=2,则有

(20)
此上界优于定理1中的上界。
定理5设图G为边数为m的n阶简单图,且ISI矩阵的零度n0 (21) 当且仅当G是由孤立点和多个完全二部图Kr,r(r为常数) 组成时等号成立。 证明由式(4)可以得到 由引理1与引理2,有 (22) 从引理1可以得知,当且仅当G是二部图时式(22)等号成立。由ISI矩阵的形式可知,二部图的ISI矩阵是对称的,G的所有非零ISI特征值的绝对值相等,所以图G是二部图,包含2个不同的ISI特征值或3个不同的ISI特征值,且每个连通部分都是正则的[13]。结合引理3可知,G由孤立点和多个完全二部图Kr,r(r为常数)组成,证毕。 定理6设图G是有n个顶点、m条边的二部图,则 (23) 证明用n+表示图G的ISI矩阵正特征值的个数。由矩阵理论的基本性质,可以得知它与负ISI特征值的个数相等。因此,有n0+2n+=n。由ISI-Estrada指数的定义和式(5)可知,若 成立,则 利用ISI-Estrada指数的基本性质,根据矩阵的特征值等图的不变量给出ISI-Estrada指数与ISI能量之间的关系。 定理7设G是有n个顶点、m条边的简单图,n+表示图G的ISI矩阵正特征值的个数,则 (24) 证明先证下界。对于任意x≥0,有ex≥1+x,对于任意x>0,有ex≥ex,则 e(ξ1+ξ2+…+ξn+)+ (n-n+)+(ξn++1+…+ξn)= (e-1)(ξ1+ξ2+…+ξn+)+ 再证上界。对于任意x≤0,有ex≤1,根据ISI-Estrada指数的定义,则 证毕。 定理8设G是有n个顶点、m条边的简单图,则 (25) 证明根据ISI-Estrada指数的定义有 证毕。 定理9设G是有n个顶点、m条边的简单图,则 EEISI(G)≤n-1+eEISI(G) (26) 证明由ISI-Estrada指数的定义有 n-1 +eEISI(G) 证毕。 定理10设G是有n个顶点、m条边的简单图,则 (27) 证明设n+、n0、n-分别为ISI矩阵的正、零、负特征值的个数,ξ1≥ξ2≥…≥ξn+为图G的ISI矩阵的正特征值,ξn-n-+1,…,ξn为ISI矩阵的负特征值。由ISI能量的定义有 由算数几何平均不等式有 同理, 对于ISI矩阵的零特征值,有 故 证毕。 1) 利用ISI-Estrada指数的基本性质,考虑ISI-Estrada指数与图的顶点数和边数等图不变量之间的关系,分别给出了ISI-Estrada指数的上下界、二部图的ISI-Estrada指数的上下界、ISI-Estrada指数与ISI能量之间的关系。 2) 仅研究了二部图这一类特殊图的ISI-Estrada指数的界,下一步将研究其他特殊图的ISI-Estrada指数的界,进一步刻画更精确ISI-Estrada指数的界。

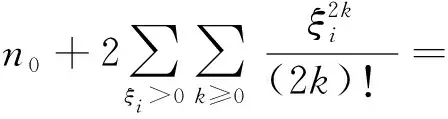

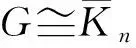
3 图的ISI-Estrada指数与ISI能量之间的关系


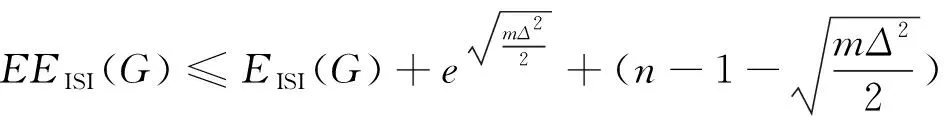
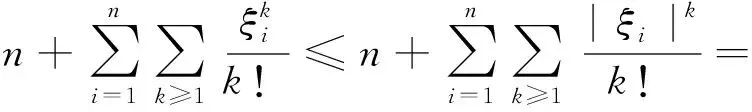

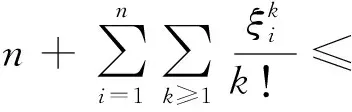

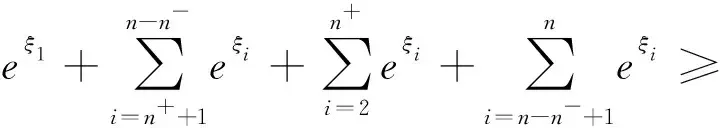
4 结论
