分布式电驱动车辆垂向振动系统优化及控制研究

2022-06-18孙晋伟胡晓燕

重庆理工大学学报(自然科学) 2022年5期

孙晋伟,胡晓燕

(1.“运输车辆检测、诊断与维修技术”交通行业重点实验室，济南 250357；2.西安航空学院车辆工程学院，西安 710077)

0 引言

分布式电驱动车辆以其传递效率高、节约空间、控制性能优越和响应速度快等优点在近年来得到了广泛研究[1-2]。但电机引入导致的非簧载质量增加、定转子间隙变化产生的不平衡径向力均对车辆垂向性能产生影响[3-4]。

目前，国内外对轮毂电机驱动车辆垂向振动研究主要集中在结构改进和主动控制2个方面。在结构改进方面，罗玉涛等[5]提出了一种新型内置橡胶悬置的拓扑构型来减小路面与电机耦合振动对平顺性的影响。Nagaya等[6]设计了一种可用于电机和轮毂之间的动力吸振结构，将电机质量由簧下转移至簧上，同时吸收路面传递至电机的振动能量。针对轮毂电机不平衡径向力产生的垂向振动负效应，Qin等[4]研究了不同路面等级、不同车速下“车身向”和“车轮向”动力吸振器对垂向性能的改善程度，并通过多体动力学仿真验证了所提出方案的有效性。尽管采用隔振结构可显著提升电动车垂向振动性能，但现有研究主要以结构设计为主，未考虑多工况下系统参数的优化匹配。

在主动控制方面，Katsuyama等[7]利用非簧载质量负天棚阻尼控制器来提升乘坐舒适性，改善车身在中频附近的振动。Shao等[8]提出了一种输出反馈控制器来提升轮毂电机驱动车辆垂向性能，但该方法以传统主动悬架控制为主。Ma等[9]在动力吸振结构的基础上增加了轮内主动减振器来消除簧下质量增加对平顺性的影响，但忽视了电机的不平衡径向力与路面输入之间的耦合关系。此外，现有主动控制以悬架或隔振器单独控制为主，对二者综合控制的相关研究较少。考虑到实际轮毂电机-悬架系统为复杂的非线性系统，且不同路面输入对系统性能影响较大。为减少非簧载质量增加及路面和电机耦合带来的垂向负效应，可在系统参数优化匹配的基础上进行主动控制来提升垂向性能。

针对轮毂电机悬架与吸振器参数匹配和主动振动控制的问题，基于布谷优化搜索典型路面激励下的最优参数，并结合天棚和地棚阻尼，提出了一种适用于轮毂电机悬架系统的混合控制方法，实现分布式电驱动车辆垂向振动系统参数优化及振动抑制的目标。

1 系统模型

1.1 悬架模型

轮内动力吸振器由电机定子与车辆轴承之间布置的弹簧和阻尼组成，该结构可同时将电机质量和制动器质量转化为轮内悬浮质量。带有动力吸振器的轮毂电机悬架模型如图1所示。

图1 轮毂电机-悬架系统模型示意图

分布式电驱动车辆垂向动力学模型可表示为

(1)

式中：mb、mk和mw表示簧载质量、车轴质量和非簧载质量；xb、xk、xw及其一阶、二阶导数分别表示簧载质量、车轴质量和非簧载质量的垂向位移、垂向速度及垂向加速度；mr和ms为电机定子和转子质量，xs、xr及其一阶和二阶导数分别为电机定转子的垂向位移、垂向速度及垂向加速度；xz为路面不平度输入；ks、ksa和kt分别表示悬架刚度、轴承刚度以及轮胎刚度；kd和kb分别为吸振器刚度和轮毂轴承刚度；cs和Cd为悬架与吸振器阻尼；Fd为定转子间隙变化产生的垂向不平衡径向力。

1.2 开关磁阻电机模型

采用四相8/6极开关磁阻电机，为表示开关磁阻电机的动态特性，需要对电机的电流、电感及位置进行准确描述。假设开关磁阻电机各相电磁参数及结构对称，则电机第k相的电动势平衡方程为

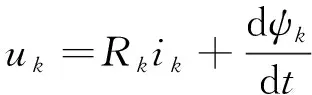
(2)

式中：uk、ik、Rk分别表示k相绕组电压、电流和电阻。ψk为k相磁链，可表示绕组电流与转子位移角的函数。

ψk=ψ(i1,i2,…,iq;θ)

(3)

式中:q为定子相数。开关磁阻电机各相间互感远小于自感，忽略相间互感可得k相磁链方程

(4)

式中:Lk(ik,θ)是由转子位置θ和绕组电流ik所表示的定子相自感，则式(2)可展开为

(5)

式中，ω表示转子旋转角速度。由式(5)可得定子绕组电流

(6)

由于每相电感是周期性的，且相电感的谐波分量远小于基波分量，因此可采用傅里叶级数的前3项来表示与转子位置相关的相自感[10]。

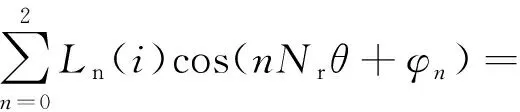
L0(i)+L1(i)cos(Nrθ+φ1)+

L2(i)cos(2Nrθ+φ2)

(7)

式中：Nr为转子极数，φn代表第n次谐波量的相角且φn=nπ。L0(i)、L1(i)及L2(i)可表示为

(8)

式中:La(i)=L(0,i)表示极对齐位置电感，Lu(i)=L(π/Nr,i)表示未对齐电感，Lm(i)=L(π/2Nr,i)表示中间位置电感。由于在非对齐位置不存在饱和现象，因此Lu(i)可看作与电流无关的常数，La(i)和Lm(i)可拟合为如下多项式[11]：

(9)

将式(8)和(9)代入式(7)中可得第k相电感

(10)

将式(10)代入式(4)可得到k相磁链方程

(11)

开关磁阻电机单相输出的机械能可表示为

(12)

根据机电能量转化，可得广义电磁力Fk

(13)

对四相(8/6)极开关磁阻电机而言，其输出的总广义力为

(14)

式中，k=1,2,3,4分别表示不同相的力。x为广义位移量，可代表转子位置角位移θ、定转子间气隙lg、定子铁片堆叠厚度lz，分别对应于电机的电磁驱动力、径向电磁力及轴向力。轴向力对车辆动力学影响较小，一般不予考虑，则电机电磁驱动力矩和径向电磁力可表示为

(15)

由式(11)可知，忽略ik为分母的项，k相磁链对转子位置角位移θ的简化偏微分方程为

(16)

将式(16)代入电磁驱动力矩方程(15)中，可得电机输出扭矩为

(17)

假设定转子间气隙的垂直绝对位移为ε，忽略凸极边缘磁通，SRM第k相绕组不平衡径向电磁力为

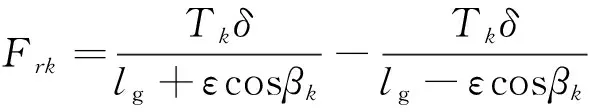
(18)

式中：Tk为k相绕组驱动力矩；lg和δ为定转子间隙及其凸极的重合角；βk为定子和转子的凸极重合时极轴与y轴之间的夹角。对四相开关磁阻电机，该角度可以表示为βk=(k-1)π/2,k=1,2,3,4。则不平衡径向力之和可表示为

(19)

不平衡径向力、转角和电流之间的关系如图2所示。由图2可知，偏心和相电流越大，开关磁阻电机产生的不平衡径向力就越大。

图2 开关磁阻电机不平衡径向力、转角和电流之间的关系曲面

2 悬架与动力吸振器参数匹配

2.1 问题描述

为实现悬架和动力吸振器的最优参数匹配，选取簧载质量加速度、轮胎动位移和定转子间隙作为优化指标，单轮激励下的最优目标函数为

(20)

式中:X代表优化变量，包括悬架和吸振器参数；JΩ(X)为工作区间Ω内的适应度函数；facc(X)、ftd(X)和fmgd(X)分别为簧载质量加速度、轮胎动位移和定转子间隙。

上述优化目标函数主要针对单一路面输入，为使车辆在不同路面激励下均获得最优性能，需综合考虑多种路面不平度下的参数匹配。选取典型的B、C、D级路面为模型干扰输入进行优化匹配，车速为60 km/h，车辆总行驶时间为30 s，分别在B、C、D级道路上行驶10 s，如图3所示。

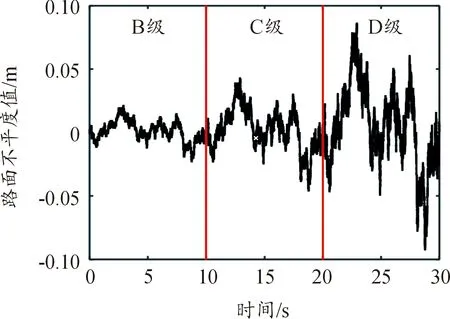
图3 不同路面类型的粗糙度值曲线

多路面输入下最优目标函数可表示为

(21)

式中：SΩ(X)为多种路面激励下的适应度值;JB(X)、JC(X)和JD(X)分别表示B、C、D级路面激励下目标函数(20)的值。通过加权系数可将以上多目标优化转化为式(22)所示的单目标优化问题

(22)

采用上述归一化方法，式(20)可表示为

(23)

式中:λi和wi为权重系数，且λ1+λ2+λ3=1，w1+w2+w3=1。为了降低悬架撞到限位块的概率，悬架动行程约束应满足σ(fsd)/|fsd|≤1/3。

2.2 布谷优化算法

布谷优化是一种模拟布谷鸟寻巢产卵行为的全局搜索方法，具有参数少、实现简单等优点，其稳定性和收敛速度均优于遗传算法和粒子群算法[12]。布谷优化的基本流程如图4所示。

图4 布谷优化流程框图

布谷鸟在寻巢飞行过程中表现出莱维飞行特性，布谷优化通过结合局部和全局随机游走策略可有效扩大搜索范围，增加种群多样性。局部随机游走可表示为

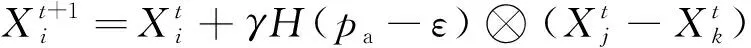
(24)

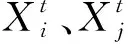
(25)

α>0为步长比例因子，莱维随机数L(λ)可表示为

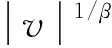
(26)

式中：u和v服从标准正态分布；s表示步长；β∈[0,1]，φ值为

(27)

为揭示悬架和动力吸振器参数与路面输入之间的关系，选择鸟巢个数为200，迭代次数为100。单一路面激励目标函数权重为w1=0.5，w2=0.3，w3=0.2，其中乘坐舒适性为主要优化目标。多路面激励目标函数权重值均为1/3，表示3种不同路面输入下优化目标相同。布谷优化迭代过程如图5所示。由图5可知，搜索过程在20代内收敛到最终的适应度值。

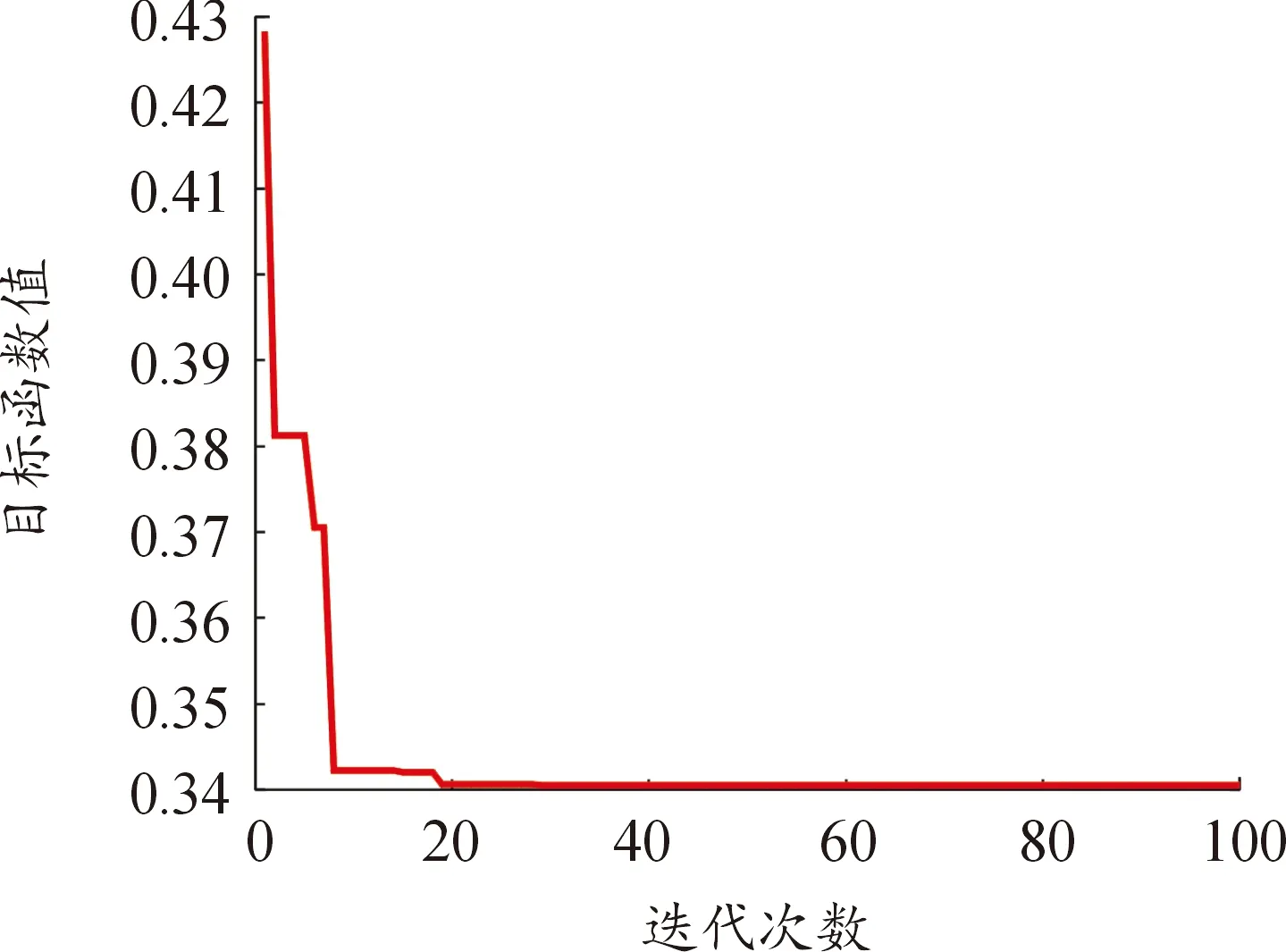
图5 布谷优化算法进化过程

3 混合半主动控制器设计

考虑到电机悬架系统的特殊结构，控制器设计过程中需同时考虑路面激励对簧载质量加速度、轮胎动位移以及电机定转子间隙变化的影响。因此，设计的混合控制器包含有2个假想的天棚阻尼和1个地棚阻尼，理想混合控制模型如图6(a)所示，等效混合控制模型如图6(b)所示。

图6 轮毂电机悬架控制模型

包含有天棚和地棚阻尼的理想混合控制模型可表示为

(28)

式中：csky1、csky2和cgrd分别表示簧载质量天棚阻尼系数、定子质量天棚阻尼系数和地棚阻尼系数，csp和cdp表示被动模型悬架和吸振器阻尼系数。可控阻尼安装在悬架和吸振器减振器位置，且簧载质量和定子质量均受地棚阻尼系数的影响，因此等效混合控制方程可表示为

(29)

通过比较动力学方程(28)和(29)，可得混合阻尼系数

(30)

由于天棚和地棚阻尼系数直接影响到控制器的控制效果，上述参数的获取可描述为以提升平顺性和操稳性为目标，以悬架行程和定转子间隙为约束的多目标优化问题：

利用文献[13]中所述的多目标优化方法得到优化的控制参数，舒适性和操稳性所对应的帕累托前沿如图7所示。

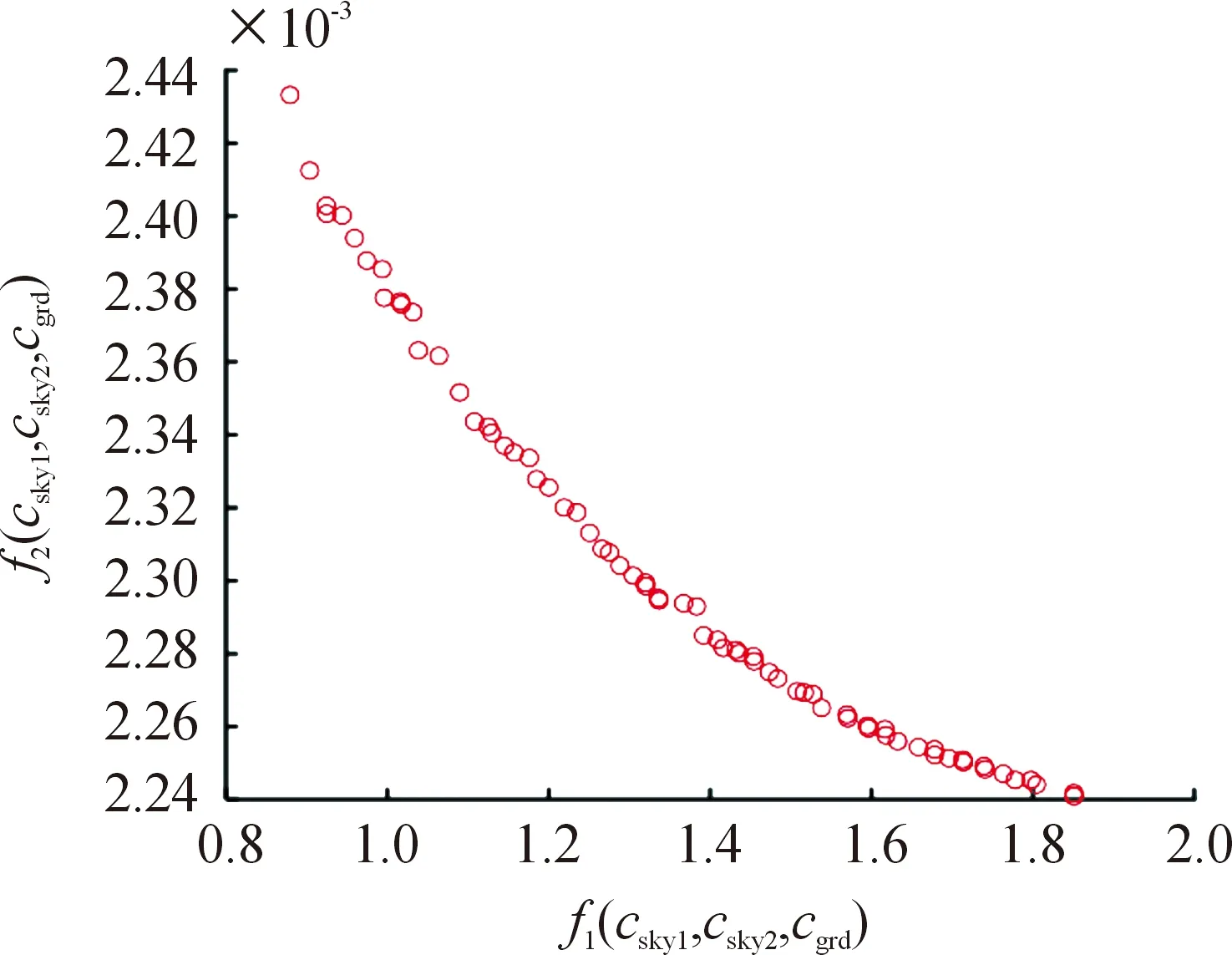
图7 帕累托最优解集

4 仿真分析

轮毂电机悬架模型参数如表1所示，系统性能指标包括簧载质量加速度(SMA)、悬架动行程(SD)、轮胎动位移(TD)和磁隙变形(MGD)。

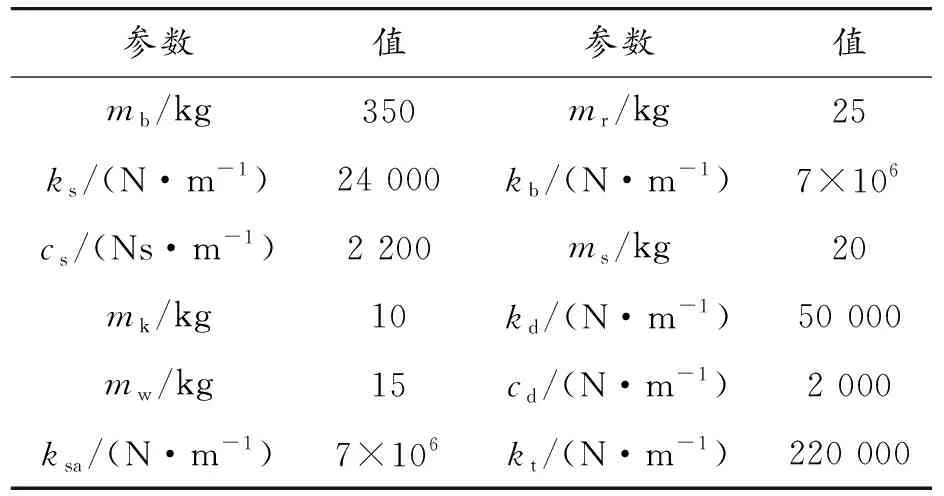
表1 模型参数

4.1 参数优化匹配

基于布谷优化算法对悬架与吸振器参数进行优化匹配，优化后的参数如表2所示。

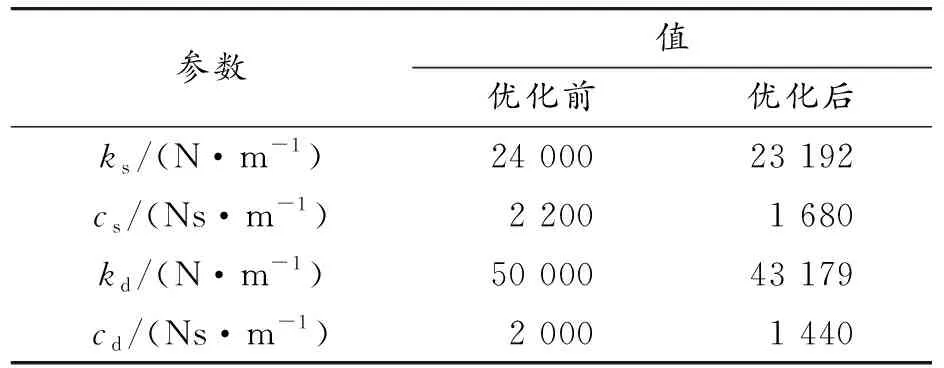
表2 优化结果

优化前后3种典型路面激励时域响应如图8所示。由图8可观察到，系统响应随着道路等级增加而增加。优化后的簧载质量加速度、轮胎动位移和磁隙变形时域幅值较优化前有所减小，表明经过优化的车辆舒适性、操稳性有所提升，且由电机定转子间隙变化引起的径向力减小。优化后的悬架动行程较优化前有一定的增加，但均能满足不同路面下的约束要求。

图8 优化前后轮毂电机悬架系统响应曲线

优化前后系统响应均方根值如表3所示。由表3可看出，B、C、D级路面激励下，优化后的簧载质量加速度、轮胎动位移、磁隙变形均方根值都有一定程度地减小，其中磁隙变形均方根值减小最为显著，其次为簧载质量加速度和轮胎动位移。B、C、D级路面激励下磁隙变形分别减小了13%、12.9%和13.4%，簧载质量加速度分别减小了9.3%、9.32%和11.2%。3种路面激励下振动响应性能提升表现出相似性，这与多路面激励优化目标函数的权重选取有关。

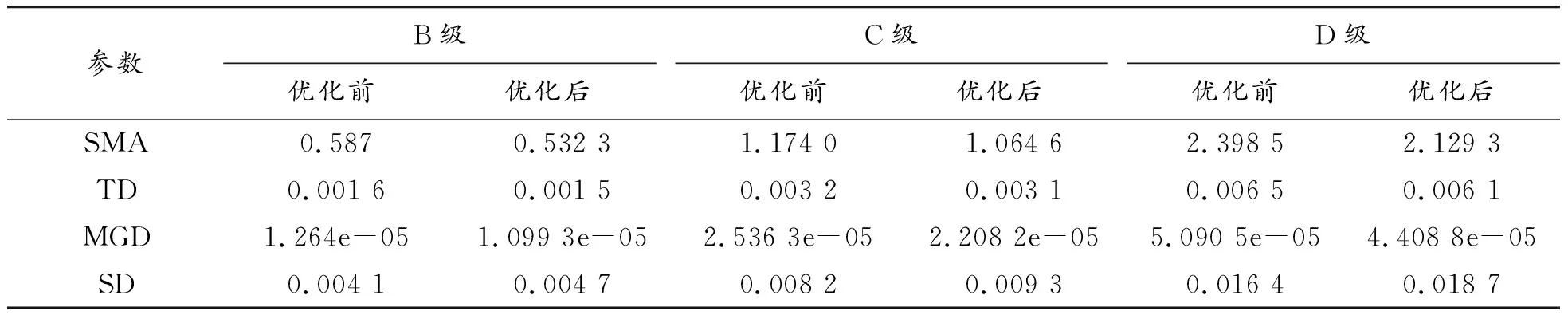
表3 优化前后响应均方根值

4.2 混合控制效果分析

为更直观地显示混合半主动控制的效果，以C级路面激励下混合控制和被动模型的动态响应进行对比，车速为60 km/h。优化得到的半主动控制参数csky1、csky2和cgrd分别为2 272、927、204 N/s，被动模型阻尼参数csp和cdp分别为800、800 N/s。轮毂电机悬架系统时域响应如图9所示。

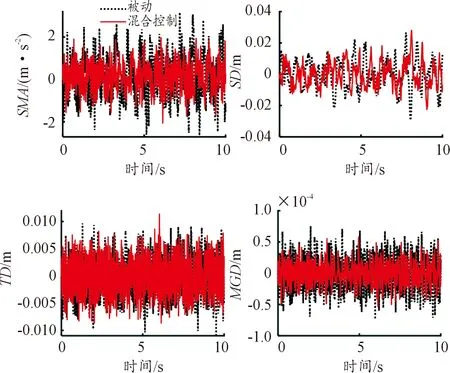
图9 系统时域响应曲线

图9中混合控制器的簧载质量加速度和磁隙位移与被动系统相比显著降低，表明混合控制器可有效提升乘坐舒适性，减小路面激励对电机定转子间隙变化的影响。与被动模型相比，悬架动行程和轮胎动位移均有所减小，在保持悬架行程约束的同时提升了车辆的操稳性。

混合控制与被动系统响应均方根值如表4所示。由表4可知，采用混合控制的轮毂电机悬架系统簧载质量加速度均方根值减小了34.79%，轮胎动位移均方根值减小了6.45%，即车辆的平顺性和操稳性得到提升。悬架动行程和定转子间隙都在约束范围之内，且二者相较于被动系统分别提升了10.75%和25.81%，即采用混合控制可有效提升车辆垂向性能，且改善了电机的工作环境。

表4 响应均方根值

为进一步验证混合控制器的性能，对轮毂电机悬架系统频域响应进行分析，如图10所示。

图10 系统频域响应曲线

由图10(a)可看出，采用混合控制器可减小簧载质量在固有频率附近的幅值；由图10(b)轮胎动位移频域响应可看出，半主动和被动系统在高频范围内表现出相似的特性，但半主动系统在固有频率附近幅值有一定的减小；图10(c)表明，采用混合控制器的磁隙变形在低频和中频范围内幅值均小于被动模型，可减小不平衡径向力对垂向系统的影响。由上述分析可知，频域系统响应与时域响应结果保持一致，验证了所提出混合控制方法的有效性。