基于DVMD和SSAE的柴油机混合故障诊断

2022-06-17白雲杰贾希胜梁庆海

振动与冲击 2022年11期

白雲杰，贾希胜，梁庆海

(1. 陆军工程大学，石家庄 050003； 2. 河北省机械装备状态监测与评估重点实验室，石家庄 050003)

随着现代工业的发展，柴油机目前已广泛应用于工业生产、交通运输和国防军用装备等领域，因此柴油机的状态监测对于保障设备工作的稳定性和可靠性具有重要意义[1]。由于柴油机复杂的结构和恶劣的工作环境，其有效故障诊断成为一个具有挑战性的问题，长期以来受到研究人员的广泛关注[2-4]。

基于振动信号的诊断方法目前被广泛应用于机械设备故障诊断中，柴油机缸盖振动信号因其蕴含丰富的运行状态信息且信号采集方便、诊断速度快，对其进行分析成为柴油机故障诊断的主要方式之一[5]。由于柴油机缸盖振动信号混合了多种激励源信号和强背景噪声，在各种信号成分和干扰的综合作用下，使其呈现非线性、非平稳的特点[6]。因此如何采用合适的信号处理手段对缸盖振动信号进行处理以提取故障特征，是当前柴油机故障诊断的关键。

蒋佳炜等[7]提出了基于小波包能量谱特征提取和模糊熵特征选择的柴油机故障诊断方法，但需要选择合适的小波包分解层数和小波基函数。陈俊柏等[8]针对机载燃油泵提出了一种基于经验模态分解(empirical mode decomposition, EMD)和支持向量机(support vector machine, SVM)相结合的故障诊断方法。张俊红等[9]采用局部均值分解(local mean decomposition, LMD)方法提取气门的故障特征。EMD和LMD方法虽然可以自适应分解非平稳信号，但都存在模态混叠现象和端点效应。Dragomiretskiy等[10]提出了变分模态分解(variational mode decomposition, VMD)，通过基于变分问题取代递归分解模式，改善了模态混叠问题，提高了对于噪声的鲁棒性。为了解决变分模态分解层数K需要人为设定的问题，本文基于散布熵提出一种改进的VMD(dispersion entropy variational mode decomposition，DVMD)方法确定分解层数K，避免主观选取产生的缺陷和误差。

当前深度学习发展迅速，广泛应用于图像处理、语音识别、目标检测、信息检索、自然语音处理等领域[11]。在深度学习模型中，稀疏自编码器作为一种重要结构，能通过堆栈的方式实现深层次特征提取，被广泛应用于各个领域[12-14]，但其在柴油机故障诊断方面研究很少。本文提出了一种基于散布熵改进的变分模态分解和反向微调的堆叠稀疏自编码器(stacked sparse auto-encoder, SSAE)相结合的方法对柴油机混合故障状态进行识别。首先对缸盖振动信号进行变分模态分解，通过计算各分量散布熵确定分解层数K和有用分量，然后对各分量分别提取时域特征和小波能量特征，构建混合特征向量，输入到堆叠稀疏自编码器中预训练Softmax分类器，接着使用原始混合特征对整个神经网络进行微调,最终实现柴油机混合故障诊断。

1 DVMD基本原理

1.1 变分模态分解

变分模态分解(variational mode decomposition, VMD)算法是构造和求解变分问题，将原信号f分解成K个本征模态函数(intrinsic mode function, IMF)分量uk(t)，满足各分量之和等于输入信号的条件下，通过迭代过程不断更新中心频率和带宽，最终得到IMF带宽之和最小的IMF分量，具体步骤如下：

(1) 通过Hilbert变换，获得每个本征模态分量uk(t)的解析信号的单边频谱，即：

[δ(t)+(j/πt)]*uk(t)

(1)

调整各本征模态的中心频率到基频带上：

{[δ(t)+(j/πt)]*uk(t)}e-jωkt

(2)

式中：δ(t)为冲激函数；*为卷积计算

(2) 计算以上解调信号梯度的平方L2范数，估计出各本征模态分量的带宽。建立约束变分模型表达式

(3)

(3) 其次是变分问题的求解，该求解过程需要引入二次项惩罚因子α和Lagrange乘法算子λ，将约束变分问题转变成非约束变分问题，其中增广Lagrange函数如下

(4)

式中：α为足够大的正数，保证信号的重构精度；λ(t)能使约束条件保持严格性。采用交替乘子方向算法(alternate direction method of multipliers, ADMM)[15]不断更新各分量的中心频率和带宽，并寻求Lagrange函数的鞍点。最终实现信号的自适应分解。

1.2 DVMD方法

散布熵(dispersion entropy, DE)是2016年由Rostaghi等[16]提出的一种新的衡量时间序列复杂程度的算法，其克服了排列熵没有考虑幅值大小的缺点，具有稳定性好，计算速度快的特点[17]。计算过程如下：

(1) 利用正态分布函数作为非线性归一化函数，将序列x= {x1,x2,…xN}归一化映射到y= {y1,y2,…yN}，其中N表示序列长度，y为以序列x的均值和标准差值为相应参数的正态分布在x中的值处所计算的累积分布值，y∈(0,1)。

(2) 通过线性算法将y映射到[1,c]范围内的整数，得到序列

zjc= int(cyj+0.5)

(5)

式中：c为类别数；int为取整。

(3) 计算嵌入向量和散布模式wv0…vm-1(v=1,2,…，c),并计算所有散布模式的概率P

(6)

(4) 使用信息熵的定义，计算原序列散布熵

(7)

根据散布熵的计算方法可以发现，当全部散布模式概率相等时，散布熵具有最大值。散布熵值越大，时间序列复杂程度越大，因此本文采用散布熵来确定VMD分解层数。通过VMD分解得到的各IMF分量的散布熵变化转折点确定分解层数K和包含有用信息的IMF分量。

2 深度神经网络构建

稀疏自编码器(sparse auto-encoder, SAE)作为一种神经网络模型，基于自编码器增加了稀疏性限制以提高网络性能，可通过无监督学习数据特征，由输入层、隐藏层、输出层构成[18]。其包括编码和解码两个过程，输入数据通过编码得到隐藏层，隐藏层通过解码重新获得输入数据，通过最优化求解最小输出输入误差。本文通过两层稀疏自编码器和Softmax分类层构建深度神经网络(deep neural network, DNN)，网络结构如图1所示。将两层SAE堆叠构成SSAE网络，将第1层SAE隐藏层输出特征作为第2层SAE输入，使用梯度下降法训练网络并迭代更新网络各层权重和偏置，使用第2层SAE输出特征来有监督地训练Softmax层以初始化参数，然后使用原始训练数据和标签有对整个深度神经网络参数进行微调优化，最终利用训练后的模型进行故障诊断。

图1 深度神经网络结构Fig.1 The structure of deep neural network

3 DVMD-SSAE算法流程

针对柴油机自身结构复杂，缸盖振动信号包含不同程度的噪声，直接计算原信号时域特征值容易因噪声信号干扰产生误差，而经过VMD分解能起到良好的降噪效果，并将复杂混叠信号中的关键分量进行提取。同时单一特征不能完全表征柴油机的故障模式，稀疏自编码器能解决多特征筛选和融合的问题，因此本文使用改进的DVMD算法与堆叠稀疏自编码器相结合的方法对柴油机混合故障进行诊断，具体步骤如下(流程如图2)。

图2 DVMD-SSAE故障诊断流程Fig.2 Fault diagnosis process of DVMD-SSAE

(1) 计算VMD分解后各IMF分量的散布熵值，观察散布熵变化转折点确定分解层数K,选取散布熵转折点较小的IMF分量作为代表关键故障信息的信号进行分析。

(2) 分别计算每个IMF分量的14个常见时域特征和小波包分解能量特征构建特征向量。

(3) 将2层稀疏自编码器堆叠后与Softmax分类层构建深度神经网络。

(4) 划分训练集和测试集，设置训练集标签和测试集标签。将训练集输入堆叠后的稀疏自编码器中进行特征优化，将得到的优化后特征和训练标签输入Softmax进行参数预训练，然后将训练集和标签输入构建的深度神经网络中对整个网络进行微调。

(5) 将测试集输入经过微调的深度神经网络中，得到不同故障模式的诊断结果。

4 试验与分析

4.1 柴油机预置故障试验系统

为了验证本文所提出方法的有效性，依托陆军工程大学石家庄校区实验室搭建的柴油机预置故障试验台进行试验。本试验研究对象是由一汽解放汽车有限公司无锡柴油机厂所制造的六缸高压共轨柴油发动机，其基本技术参数见表1。试验台如图3所示，试验共设置7种混合故障模式，如表2所示。

表1 柴油发动机技术参数Tab.1 Technical specifications of the diesel engine

表2 故障模式设置Tab.2 Failure mode setting

图3 柴油机预置故障试验台Fig.3 Diesel engine preset failure test bench

其中，某缸失火故障通过断开该缸电源线来实现，空气滤清器堵塞通过加装进气罩来实现，喷油泵供油不足通过故障件替换来实现。具体故障设置见图4。

(a) 断开喷油器电源线

(b) 加装进气罩

试验过程中，使用北京中科泛华公司的数据采集机箱(PXI-9108)、数据采集卡(PXI-3342)和上海北智公司的压电式振动加速度传感器(BW14100)。振动加速度传感器垂直于发动机1～6缸缸盖表面进行安装，如图5所示。对发动机运行过程中缸盖振动信号进行采集，采样频率为20 kHZ，采集单个样本点数为5 000。

图5 振动传感器安装位置Fig.5 Arrangement position of vibration sensor

4.2 信号分析与特征提取

试验中选取第5通道信号进行研究，7种混合故障模式下的振动信号波形杂乱、无明显特征，因此考虑对缸盖振动信号进行处理和特征提取。以一缸失火模式为例，对其振动信号进行变分模态分解，并计算分解得到的各IMF分量的散布熵以确定分解层数K值，得到不同分解层数K下的各IMF分量散布熵见表3。本文在计算散布熵时选取嵌入维度m等于2，类别个数c为7，时间延迟d取1。

表3 不同分解层数下各分量散布熵Tab.3 Dispersion entropy of each component under different decomposition levels

通过对信号进行VMD分解后，分析不同分解层数下的IMF分量的散布熵可以知道，在分解的过程中，散布熵代表IMF分量序列的复杂程度，各IMF分量的散布熵具有一定变化趋势，散布熵越大代表分量复杂程度越高，在实际情况中，往往代表高频噪声信号和复杂干扰信号。

从表3中可以看出，当K=5时，各IMF分量散布熵出现变化转折点，说明此时已出现噪声分量和有用分量，确定VMD分解层数K=5，分解得到的各分量如图6所示，绘制各分量频谱图如图7所示。

图6 DVMD分解各IMF分量Fig.6 Each IMF component for DVMD decomposes

图7 各IMF分量频谱图Fig.7 Spectrogram of each IMF component

经过计算可知，IMF2分量的散布熵最大，说明其信号复杂程度最大，同时观察各分量频谱图可知，IMF1和IMF2均为高频分量，带宽较宽且频谱相对复杂，考虑其为复杂噪声和干扰信号，因此选取IMF3，IMF4，IMF5为包含故障特征信息的有用分量。对IMF3，IMF4，IMF5三个分量分别提取最大值、最小值、峰峰值、平均值、绝对平均值、方差、标准差、峭度、偏度、均方根、波形因子、峰值因子、脉冲因子、裕度因子共14×3个时域特征。同时对缸盖振动信号进行3层小波包分解，选取db3小波基，得到8×3维能量特征。将3个IMF分量时域特征和小波包分解能量特征组合，最终得到的单个样本数据由66维混合特征向量构成。

4.3 柴油机混合故障诊断

为了验证在不同混合故障模式下，本文所提出方法的可行性，使用4.2节中的方法构建数据集。试验数据集信息如表4所示，最终得到560个训练样本，112个测试样本。

表4 数据集信息Tab.4 Data set information

由于稀疏自编码器网络层数并非越多越好，层数太多会造成网络不稳定并增加计算时间，层数太少会产生高维特征提取不彻底的现象[19]。本文构造一个2层的堆叠稀疏自编码器网络，隐藏层节点数分别为100和30，具体参数设置如表5所示，不同参数对诊断结果影响见表6。

表5 SSAE网络参数设置Tab.5 Parameter settings for SSAE network

表6 SSAE不同参数影响Tab.6 The influence of different parameters of SSAE

将试验得到的训练样本输入本文所构建的深度神经网络中进行训练，然后将测试样本输入训练后的模型中，得到柴油机7类混合故障的诊断结果，其混淆矩阵如图8所示。

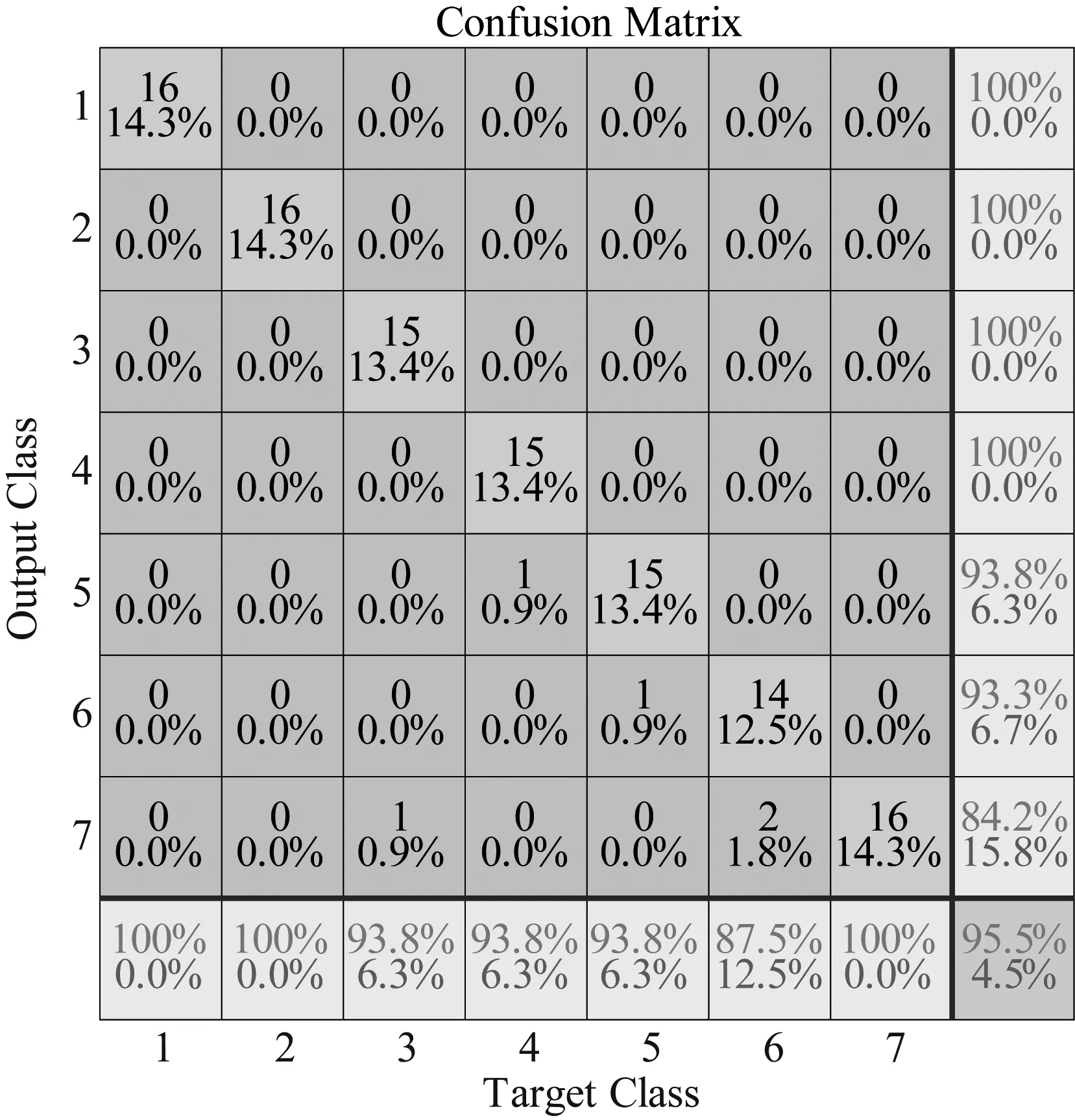
图8 诊断结果混淆矩阵Fig.8 Confusion matrix of diagnosis results

从诊断结果混淆矩阵可以看出，本文所提出的方法对柴油机7类混合故障的整体准确率达到95.5%，其中正常状态、一缸失火状态、空滤堵塞二缸失火状态3种故障模式诊断准确率达到100%，二缸失火状态、空滤堵塞状态和供油不足状态3种故障模式的诊断准确率也达到93.8%，仅空滤堵塞一缸失火状态的诊断准确率为87.5%。

考虑由于不同SSAE网络层数对诊断结果的影响，分别构建M层SSAE网络，其中M= 1，2，3，4，5。不同网络层数下的混合故障识别结果如图9所示。从图中可以看出，在相同数据样本输入不同层数构建的SSAE网络中，诊断结果存在明显差异，在SSAE为2层时，诊断准确率达到最大值。随着网络深度的增加，准确率发生波动，当SSAE层数增加为5层时，准确率下降到74.1%。观察不同网络层数下模型训练时间的变化如图10所示，结果说明SSAE网络层数增加，并不会带来诊断准确率的提高，同时随着网络层数增加，训练时间变长，效率降低。

图9 不同层数SSAE诊断结果Fig.9 SSAE diagnosis results of different layers

图10 不同层数SSAE训练时间对比Fig.10 Comparison of SSAE training time with different layers

为了探究本文所提出方法所构建混合特征在柴油机故障诊断方面的有效性，将相同的数据样本直接提取原信号时域特征后输入堆叠稀疏自编码器(Tfeature-SSAE)，原信号小波包分解能量特征输入堆叠稀疏自编码器(Wfeature-SSAE)，原信号混合特征输入堆叠稀疏自编码器(Cfeature-SSAE),本文提出的DVMD分解后提取时域特征输入堆叠稀疏自编码器(DVMD-SSAE(T))，DVMD分解后提取小波包能量特征输入堆叠稀疏自编码器(DVMD-SSAE(W))，观察诊断结果如表7所示。

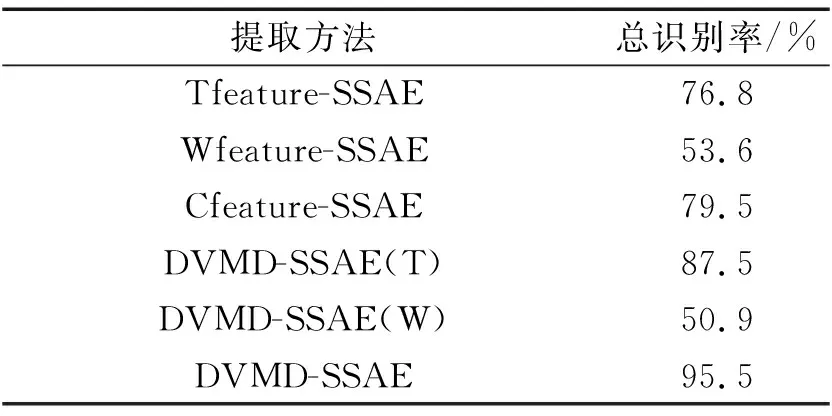
表7 不同特征诊断结果Tab.7 Diagnosis results of different characteristics

由结果可以看出，针对7种混合故障模式情况下，对柴油机缸盖振动信号直接提取时域特征和小波包能量分解特征诊断效果不好，且小波包分解能量特征总识别率仅53.6%。使用本文所提出的DVMD分解算法对缸盖振动信号进行处理后，直接提取时域特征，识别率达到87.5%，混合特征识别率达到95.5%，验证了本文所提出的DVMD分解算法对柴油机缸盖信号处理的有效性，能有效分离出噪声信息和有用信息；同时发现对信号直接提取小波包分解能量特征比经过DVMD分解后提取小波包能量特征识别率略高，考虑可能是由于经过DVMD分解后分离了噪声信号，相比于原始信号在能量上衰减了所导致，但整体上影响不大；通过对比结果也验证了本文所构建混合特征在柴油机混合故障识别上的有效性。

同时，为了验证本文所提出方法的优越性，对试验中的相同数据样本使用经验模态分解和堆叠稀疏自编码器相结合的方法(EMD-SSAE),本文所提出DVMD与BP神经网络结合的方法(DVMD-BP),DVMD与支持向量机结合的方法(DVMD-SVM)，以及DVMD与当前研究较多的两类优化支持向量机参数方法：粒子群优化支持向量机方法(DVMD-PSO-SVM)、灰狼优化支持向量机方法(DVMD-GWO-SVM)对柴油机混合故障进行诊断，识别结果如表8所示。通过比较不同方法的诊断准确率可以看出，本文所提出的DVMD-SSAE方法对于柴油机7种混合故障模式的诊断效果最好。