混合式配电变压器数字控制系统离散域建模与稳定性分析

高亚晨，梁得亮，柳轶彬，张立石，李大伟，吴子豪

（1. 西安交通大学 电力设备与电气绝缘国家重点实验室，陕西 西安710049；2. 西安交通大学 陕西省智能电网重点实验室，陕西 西安710049；3. 国网陕西省电力公司电力科学研究院，陕西 西安710100）

0 引言

随着新能源产业和电力电子技术的迅速发展，越来越多的复杂电力设备接入配电网，这些设备虽然功能丰富，操作方便，但往往会给电网带来诸如高频谐波和无功分量注入以及电压波动等问题［1-2］。这对传统配电变压器提出了新的技术挑战，具体而言，传统配电变压器只负责电压等级变换，显然已经不满足日益复杂的电网电压调控要求。此外，变压器本身也需要具备一定的补偿能力来应对畸变、无功负荷的危害。于是，固态变压器、电力电子变压器［3］以及混合式配电变压器HDT（Hybrid Distribution Transformer）等新型可控变压器相继出现。其中，HDT是以传统变压器为基础，结合有源滤波器、动态电压调节器等电力电子装置升级改造而成［1］。相比于其他类型的可控变压器，HDT在实现无功补偿、谐波治理、稳定电压等功能的前提下具备更简单的结构［3］，这对于未来构建智能配电网具有重要的意义。

目前关于HDT 的研究主要集中在连续域下［4-9］：文献［4］中提出的HDT 动态控制系统方法是针对HDT 电压电流双闭环在连续域下建模的分析方法；文献［5-8］分别提出了鲁棒预测控制、复合控制器设计方法、松弛二端口建模以及开式绕组设计方法，这些方法能使HDT 在连续域中获得良好的性能表现，但上述文献均未涉及数字控制方案的研究。

目前在离散域下对于HDT 数字控制系统的研究较少，而实际上在离散域下对HDT 数字控制系统进行建模分析十分必要。这是因为HDT 的控制系统需要使用数字控制器来实现，数字控制器延时对HDT 系统整体的稳定性及暂态特性具有重要影响，故计及延时环节的HDT 控制系统离散域建模分析更接近其实际运行情况。其中，数字信号处理器DSP（Digital Signal Processor）由于具有抗干扰能力强、控制能力好以及灵活性高等优点，被广泛应用于电力电子装置中。目前逆变器的控制也普遍采用DSP 来实现，但采用DSP 进行控制会不可避免地带来延时问题［9-10］，如当HDT 中逆变器（IVp和IVt）进行负载电压调控和谐波治理时，因经历采样、计算以及脉宽调制（PWM）过程而产生数字延时，进而对系统的稳定性造成影响。虽然目前在分析数字控制器的延时方面，有研究者提出应用高阶帕德近似法［11］来计算延时，但这样的处理方式对系统阶数有一定的要求，当系统阶数仅为1 或2 时模型精度会下降，且存在计算量过大的问题。另外，DSP 控制效果很大程度上取决于采样周期、采样精度和参数，这也为设计HDT 数字控制系统带来困难。由此可见，对数字控制下的HDT进行特性分析十分必要。

为此，本文首先建立了HDT 连续-离散混合控制模型，并推导了离散域下HDT 数字控制系统的传递函数。讨论了数字控制下比例积分（PI）参数对HDT 系统稳定性的影响，重点分析了采样周期对HDT系统稳定性的影响。最后通过仿真以及实验验证了理论分析的正确性。

1 HDT基本特性及控制结构

文献［4］中给出了HDT 的等效电路图，但其符号较多，系统特性较为复杂，考虑到变压器工程应用场景的电压等级普遍较高，而绕组阻抗数值较小，对系统的稳定性影响不大，且本文分析的重点在于数字控制下HDT 的特性，绕组阻抗并不会对HDT 系统稳定性产生关键影响，故本文分析中将忽略绕组阻抗以简化运算。本文在文献［4］给出的等效电路图基础上进行简化，并以附录A 图A1 所示的a 相HDT等效电路图为例进行说明。

由图A1 可知：HDT 系统包含主变压器（T1）、隔离变压器（T2）以及2个电力电子逆变器（IVp和IVt）［3-5］，主变压器进行正常的电压变换和功率传输，隔离变压器作为补偿装置补偿电压波动；W1—W5为各级绕组，相连的W1、W5（W5为补偿绕组）位于一次侧，W2—W4（W3、W4为控制绕组）位于二次侧，W1—W3组成T1，W4、W5组成T2。基于PWM 技术，IVp和IVt可实现HDT系统无功波动补偿和谐波抑制［5］。例如当W2侧负载存在谐波或无功等有害分量时，控制器会根据所采集的数据分析此时电流包含的谐波成分计算电流补偿量，再按照一定占空比控制开关管导通，进而通过IVp桥臂电压来控制HDT系统W3侧的电流i3，使之产生极性相反的电流分量。这是由于稳态时系统电感能量的储存和释放是平衡的，开关周期又很短，可以认为电流近似不变；并且根据三绕组变压器的磁动势平衡原理，W2侧电流i2中谐波或不对称等有害分量能够被消除。上述过程说明了HDT 系统中IVp和IVt可以实时地补偿有害分量、抑制电压波动及消除不平衡分量，保证了HDT 系统用户侧的电能质量。

采用数字控制时需要将HDT 系统中的模拟信号转变为数字信号，以便于DSP 处理，故HDT 的实际系统是由连续-离散环节构成的复合系统。本文构建的HDT连续-离散混合控制模型如附录A图A2所示。连续环节和离散环节共同作用，实现对HDT连续-离散混合控制模型的整体控制：连续环节包括逆变器及直流母线等HDT 主体部分的控制；离散环节包括采样、坐标变换、PI控制和空间矢量脉宽调制（SVPWM）等数字信号的处理，离散环节存在于DSP芯片的数字处理过程中。

由于负载侧滤波电容Cf一般较小［6］，流经Cf的电流很小，对负载电压影响也很小，故可近似认为负载电流iL≈i2，可将iL与i2合并，简化数字控制框图。由附录A 图A3 可推导连续域电流控制的开环传递函数Ggi（s）与电压控制的开环传递函数Glv（s）分别为：

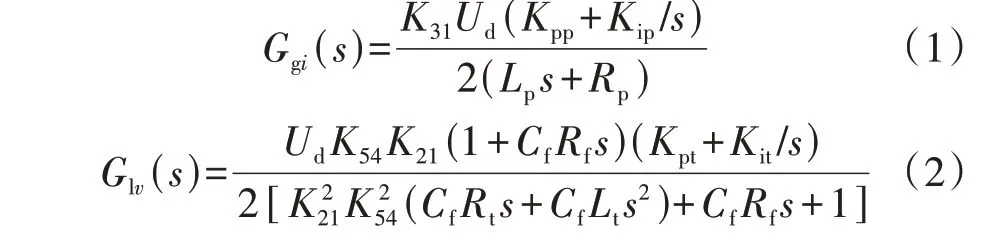
式中：Kpp、Kip和Kpt、Kit分别为IVp和IVt的比例、积分参数；Lp、Rp和Lt、Rt分别为IVp和IVt的滤波电感、集中电阻；Rf为滤波电阻；Ud为直流母线电压；K21、K31、K54分别为W2和W1、W3和W1、W5和W4间的匝数比。

对于连续域分析方法而言（以HDT 电流控制系统为例），由式（2）可得电流控制环节特征方程为：

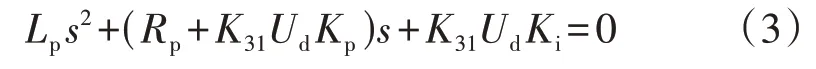
式中：Kp、Ki分别为电流控制环节对应PI控制器的比例、积分参数。根据劳斯-赫尔维茨判据，系统稳定的充分必要条件为各项系数均大于0，劳斯阵列第1列均大于0。而式（3）中参数为系统控制参数，均有正实数值，故在连续域的分析下，保持比例控制系数Kpp和Kip均大于0，即可保证系统闭环极点均位于左半平面，即电流控制系统是恒稳定的。

2 HDT数字控制系统设计

2.1 HDT计算延时和调制延时

区别于连续环节模拟控制系统设计，离散环节数字控制系统会引入固有的延时环节，包括计算延时和PWM 延时［10，12］。在数字控制系统中，为了避免开关纹波对系统的不良影响，通常在三角波载波的波峰或者波谷进行采样［12］，如图1 所示。图中，Ts为系统采样周期。

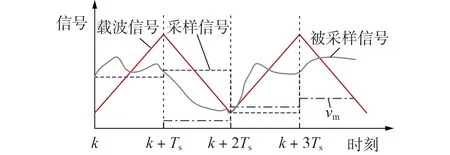
图1 PWM采样过程及延时Fig.1 Sampling and time delay in PWM

采样系统在某一时刻k处对信号进行采样，所得信号经计算后被送入DSP 得到PWM 信号vm。为避免vm和载波信号发生交载现象［13］，且采样和计算仍需要一定的时间，故在时刻k计算得到的信号需要在时刻k+Ts处装载，相对于原始信号慢了1 个周期（或称一拍），计算装载延时由此产生。该采样原理在数字控制设计时较为常见，其特点在于能够得到每个采样周期内信号平均值（或基波成分），且无需滤波环节［13］，在一定程度上优化了控制结构。由于被装载后的调制信号在一个采样周期内保持不变，在对数字控制系统进行设计时通常需要加入零阶保持器（ZOH）来描述此特性［14］。ZOH的传递函数Gzoh（s）为：

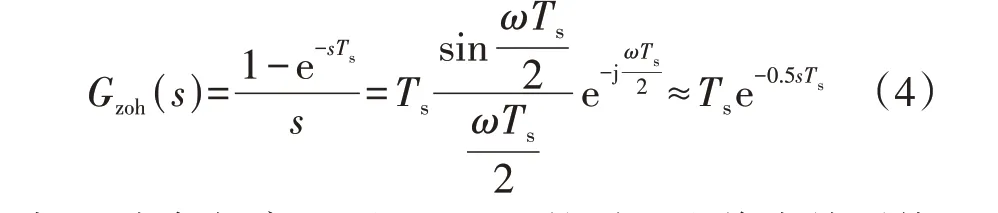
式中：ω为角频率。可见，ZOH 的引入也将会给系统带来大约0.5拍的延时。

延时项并不会改变增益大小，但会使相位发生偏移，从而降低系统的稳定裕度［15］。可以理解为在连续域中，延时环节的引入相当于给传递函数乘以一个延时因子e-ns（n=1，2，3，…），此延时项在幅频特性曲线上表现为使得相位裕度减小，系统稳定性下降。这和完全的连续域忽略延时环节的控制分析不同，故进行设计时需要考虑延时环节对HDT 数字控制系统的影响。

2.2 考虑延时的离散域控制设计

根据附录A 图A2 所示HDT 的控制系统，建立dq0 坐标系下离散域HDT 负载电压控制框图模型，如附录A 图A4所示。由前文分析可知，数字控制下会引入约1 拍的计算装载延时以及约0.5 拍的ZOH延时。计算装载1 拍延时GD1(s)和网侧电流控制器到负载电压控制器（二者均为PI 控制）的传递函数Gc(z)的表达式分别如下：

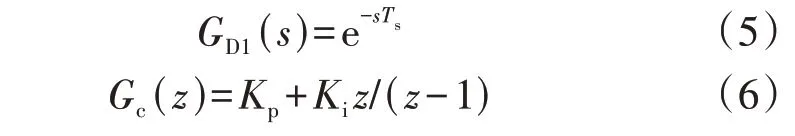
考虑到HDT 在进行数字控制分析时可能会出现频谱的混叠现象，为了更直观地分析数字控制下的HDT 特性，避免潜在频谱混叠现象的发生，本文采用双线性（Tusin）变换对HDT 控制系统离散化。Tusin 变换是连续系统到离散系统转换的常用方法之一，能够将连续域下的模拟信号变换为离散域z下的数字信号，并能通过单值对应消除频谱混叠现象［16］。Tusin 变换的基本原理是将z域和s域的关系进行进一步变换，如式（7）所示。

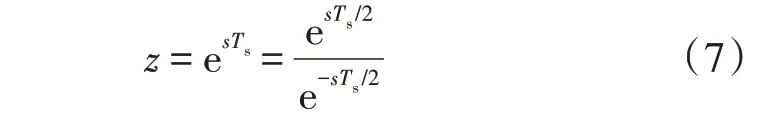
将式（7）在sTs/2=0 处进行泰勒展开，忽略高阶项，重新整理可得：

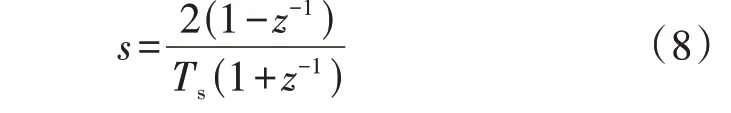
将式（8）代入式（2）可推导得离散域下HDT 电压控制环节开环传递函数，由于表达式较为复杂，为了方便说明，令N=K54K21、C1=CfRf、C2=CfRt、C3=CfLt，则式（8）可简化为：

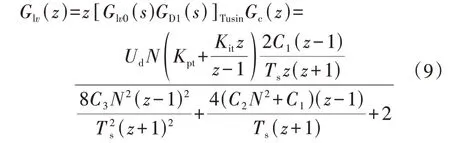
式中：z[·]Tusin表示将[·]进行Tusin 变换；Glv0(s)为附录A 图A2中负载电压u2到调制波的开环z域传递函数。由式（9）可得HDT 电压控制开环传递函数的特征方程，利用朱利稳定判据，特征方程式所有根均位于z平面单位圆内的充要条件见式（10）。

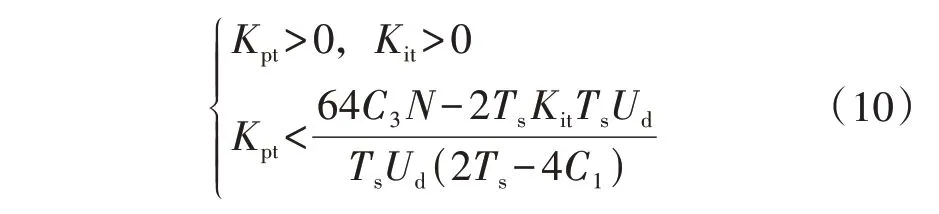
由式（10）可知，与连续域下的分析不同，在离散域的分析中，PI参数设计产生了约束条件，且和采样周期有关。当Ts很小时，PI 参数可以选取的范围就很大，反之当Ts很大时，PI选取将会受限。而在现实控制系统中，受限于芯片计算能力和物理环节，显然采样周期是不可能无限小的，因此如何选取合适的采样周期也是设计数字控制HDT 系统的一个关键因素。故为了使HDT 系统具备更好的性能，在设计HDT数字控制系统时，需要对该问题展开研究。

2.3 数字采样周期设计

采样周期是HDT 数字控制系统中的关键设计参数，一方面要避免因采样周期设置过大而导致控制不精确、波形不完整的问题，另一方面需要兼顾系统资源的合理调配，不能因为采样周期设置过小而占据太多的计算资源。由式（4）可知，采样周期通过影响控制器增益和相位进而影响控制器特性，进一步影响了数字HDT 系统的性能，故需要选取合适的采样周期。本文设计10 组不同的采样周期，分别取值为0.01、0.02、0.04、0.05、0.08、0.10、0.12、0.15、0.16、0.20 ms。不同采样周期下HDT 系统负载电压的波特图如附录A 图A5所示。由图可知，当采样周期为0.01 ms 时，系统的稳定裕度为59.2°，系统稳定性良好，但是响应速度过慢，随着采样周期的增大，系统的稳定裕度跟随减小，当采样周期为0.20 ms时，系统的稳定裕度仅为7.37°，系统稳定性很差。综上分析可得较为合适的采样周期为0.05 ms，对应的采样频率为20 kHz，此时系统稳定裕度为44.2°，系统稳定性良好，系统响应迅速。

3 仿真验证

为了验证采集、计算和延时环节对HDT 数字控制系统稳定性的影响，根据附录A 表A1进行参数设置，基于MATLAB／Simulink 仿真平台验证本文所提HDT数字控制系统设计的正确性。

在2 种采样周期（0.05 ms 和0.15 ms）下进行仿真，得到网侧电压us波形如附录A 图A6 所示。当Ts=0.05 ms 时，负载电压u2以及网侧电流is的波形如图2 所示。由图可知，由于HDT 数字控制系统在离散域下设计并进行数字采样，波形会有一定的波动。相较于连续域下模拟信号的控制分析中网侧电流三相正弦波形精度下降。这是因为逆变器IVp和IVt正常投入工作，在图2 所示的波动处进行暂态补偿，并将波动抑制到合理范围内。故当Ts=0.05 ms 时采样控制器可以实现较为快速且准确的跟随效果。系统此时以较快的速度补偿网侧电压突变并治理负载侧的电压谐波，使负载侧用户获得稳定电压，这说明当Ts=0.05 ms时HDT数字控制系统具有良好的性能。

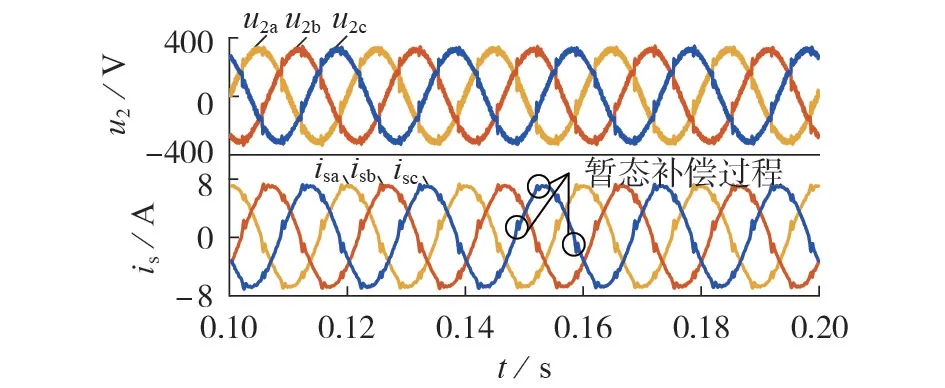
图2 当Ts=0.05 ms时u2、is波形Fig.2 Waveforms of u2 and is when Ts is 0.05 ms

当Ts=0.15 ms 时，负载电压u2以及网侧电流is的波形如图3 所示。由图可知，当Ts=0.15 ms 时，系统的补偿效果会急剧下降，负载侧电压已不能被很好地保持，稳定性很差，网侧电流包含大量谐波成分，且补偿效果因为延时过久而变得很差，对HDT 的性能有较大影响。验证了前文理论分析的正确性。

同时，为了检验本文设计的HDT 数字控制系统谐波治理能力与应对波动的暂态响应能力，首先设Ts=0.05 ms，对比HDT 数字控制系统参与谐波治理前、后（即逆变器处于不控整流工作模式下）网侧电流波形，对比结果如附录A 图A7 所示。可以看出：HDT 数字控制系统参与谐波治理前，负载电压包含大量3、5次谐波，总谐波畸变率（THD）为17.46%，此时电压失真较为严重；HDT 数字控制系统参与谐波治理后，3、5次谐波被很好地补偿，THD降为4.98%，负载电压更接近三相正弦波形，这证明了本文设计的HDT数字控制系统具备良好的谐波治理能力。

此外，检验HDT 数字控制系统应对波动的暂态响应能力，设t=0.6 s时网侧电压骤升到120%UN（UN为网侧电压额定值），t=0.8 s 恢复正常，得到负载电压和直流母线电压波形如图4 所示。由图可知：直流母线电压在约0.3 s 时即可达到设定参考值U∗d并保持稳定跟踪；当电网电压波动时，直流母线电压出现小范围的波动后快速恢复正常，响应速度较快，并使负载侧电压仍能保持稳定。这证明了HDT 数字控制系统具备良好的暂态响应能力。

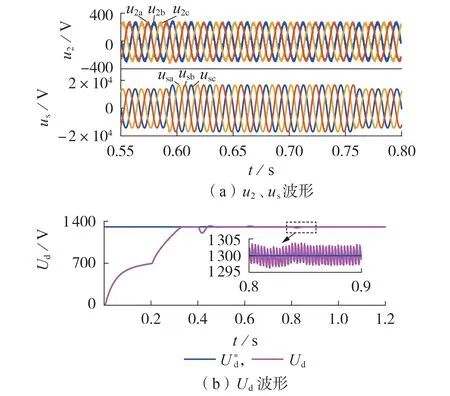
图4 当us突变为120%UN时u2和Ud波形Fig.4 Waveforms of u2 and Ud when us changing to 120%UN

4 实验验证

根据前文设计，搭建如附录A 图A8所示的HDT数字控制系统实验平台，其中包括三相交流电源、主变压器T1、副变压器T2、可变负载、IGBT 以及DSP 控制驱动板。由于实验室条件限制，电压等级低于仿真中设置电压，实验参数如附录A表A2所示。

在2 种采样周期（Ts=0.05 ms 和Ts=0.15 ms）下进行实验验证。当Ts=0.05 ms 时，负载电压和网侧电流的实验波形分别如图5、6 所示。由图可知，负载电压和电网电流波形同图2 所示仿真结果一致。对比文献［5］中采用连续域下模拟信号控制得到的网侧电流波形，利用离散域下数字信号控制得到网侧电流控制精度有所下降，这是由于数字控制下引入采样、保持、计算等环节产生了延时，仿真及实验结果验证了理论分析的正确性。在实际运用中，数字控制可以利用预测补偿延时等方法提升控制精度，如文献［17］提出的网络同步采样技术。虽然本文研究侧重于HDT 数字控制系统的离散域建模和暂态稳定性分析，但是由实验波形可知，本文所提HDT数字控制系统的基本特点和控制效果与连续域下的模拟信号控制基本相近。如图2、6 所示，网侧电流波形的毛刺处对应于系统的补偿点，这说明HDT 数字控制系统可以实时跟踪，当网侧电流波动时控制系统会给予补偿，故当前控制精度是可以接受的。

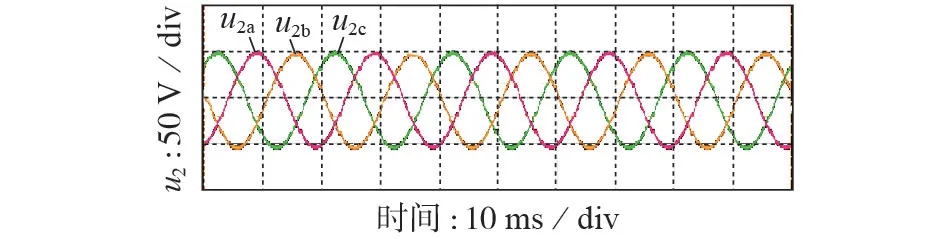
图5 当Ts=0.05 ms时u2实验波形Fig.5 Experimental waveform of u2 when Ts is 0.05 ms

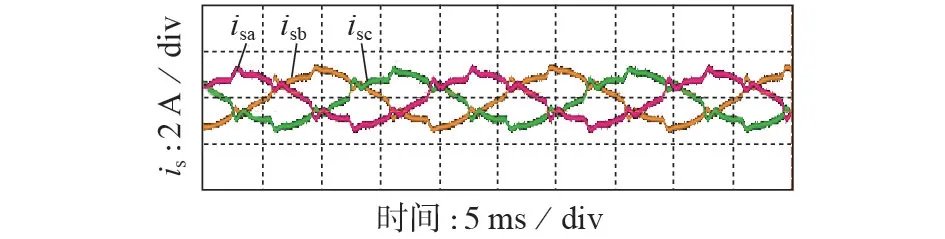
图6 当Ts=0.05 ms时is实验波形Fig.6 Experimental waveform of is when Ts is 0.05 ms

当Ts=0.15 ms 时，负载电压和网侧电流的实验波形分别如附录A 图A9、A10 所示。由图可知，当Ts=0.15 ms 时，由于采样周期增大，系统的计算能力趋近于饱和，在延时的作用下用于计算装载的时间裕度变得极其有限，对于系统的稳定性影响更为突出，负载电压和网侧电流均会出现不同程度上的纹波，系统的补偿效果下降，这与图3 所示仿真结果相一致。

同样，为了验证网侧电压波动下系统暂态响应，设置网侧电压在某一时刻突升，观察负载电压和直流母线电压的实验波形，如图7 所示。当网侧电压发生突升时，直流母线电压保持稳定，负载电压在网侧电压突变的一瞬间会跟随变大，然后很快被控制住，并保持额定值，证明本文设计的HDT 数字控制系统具备良好的暂态响应特性，由此验证了理论分析中对控制器参数分析与设计的正确性。

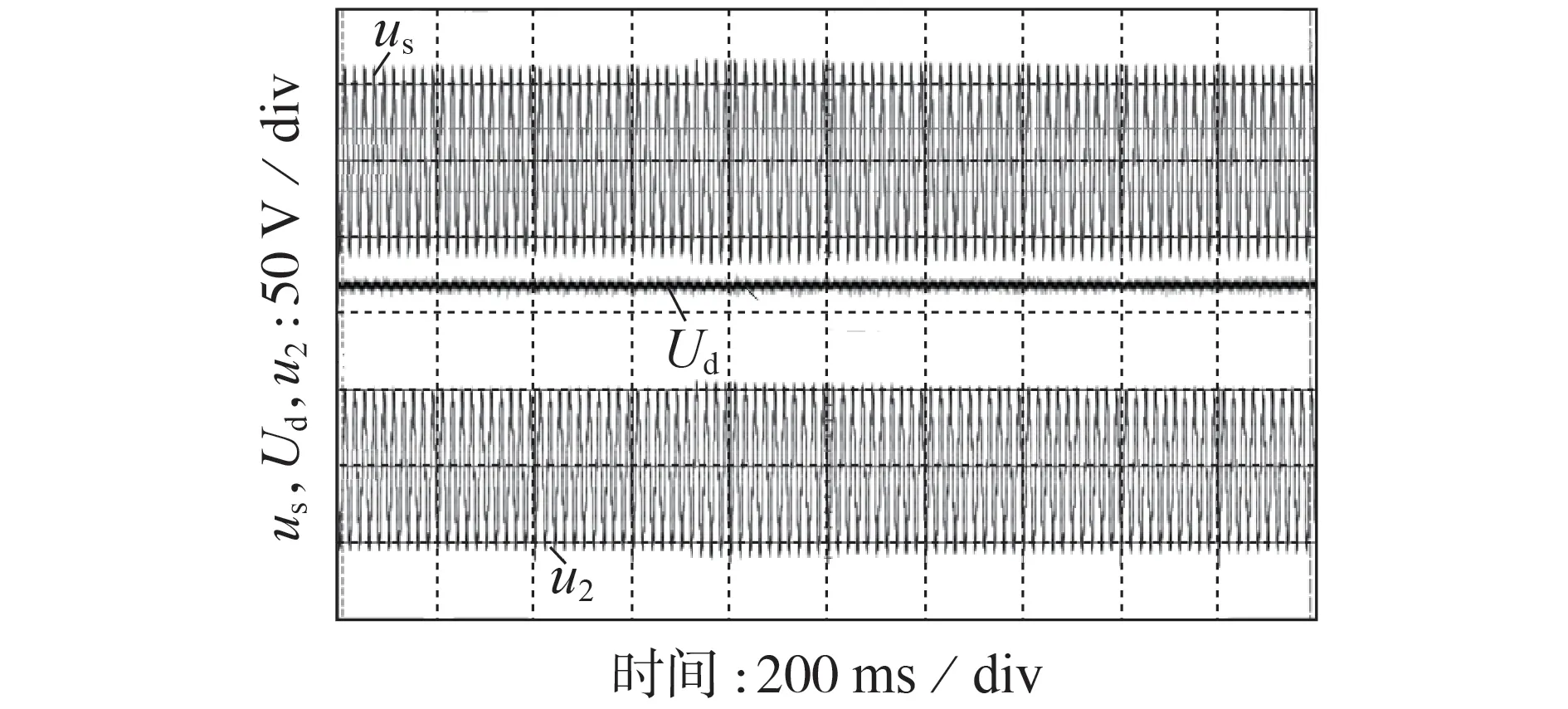
图7 网侧电压波动下系统暂态响应Fig.7 Transient response of system under grid-side voltage fluctuation

5 结语

本文提出了一种HDT数字控制系统离散域建模与稳定性分析方法。建立了考虑延时作用的HDT系统电流电压双闭环数字控制模型；通过朱利判据推导了HDT 数字控制系统PI参数的约束条件；并分析不同延时作用下稳定裕度的变化规律以及对HDT数字控制系统的性能影响；评估了延时对HDT 数字控制系统稳定性的影响，进而确定良好的控制器设计参数。仿真和实验结果验证了所提HDT数字控制系统建模方法的准确性以及稳定性分析方法的有效性。

附录见本刊网络版（http：//www.epae.cn）。