中压侧双极短路故障下改进型ISOP直流变压器的参数关系和直流电抗器电感计算
2022-06-15王志刚王小红梁帅奇王国宁曾肖明徐建松
王志刚,侯 凯,王小红,梁帅奇,王国宁,曾肖明,徐建松
(1. 智能电网保护和运行控制国家重点实验室,江苏 南京 211106;2. 南瑞集团有限公司(国网电力科学研究院),江苏 南京 211106;3. 国电南瑞科技股份有限公司,江苏 南京 211106;4. 国电南瑞南京控制系统有限公司,江苏 南京 211106)
0 引言
近年来随着电力电子技术的发展,以及风光储、充电桩和数据中心等直流电源和直流负荷的大规模接入,中压直流配电技术蓬勃发展。直流变压器DCT(Direct Current Transformer)作为中压直流配电网中的关键设备,能够实现不同直流电压等级的电网互联、直流电压大变比变换、功率控制、电气隔离等功能。另外,随着直流配电网对可靠性和自愈性要求的提高,在直流变压器自身发生故障[1-2]或直流系统发生故障时[3-4],要求直流变压器具有故障隔离和故障穿越能力。
当前工程实践中应用最多的是基于输入串联输出并联ISOP(Input Series Output Parallel)拓扑的直流变压器[5](下文简称ISOP 直流变压器),ISOP 直流变压器具有高效率、模块化设计、易维护等优势,但是传统ISOP 拓扑在面对模块冗余和直流系统故障时显得无能为力,因此改进型ISOP 直流变压器[6]应运而生,其中最典型的结构是在每一级模块前增加半桥结构和直流电抗器[7-8],该结构与增加平波电抗器的模块化多电平换流器MMC(Modular Multilevel Converter)类似[9-10]。文献[11-14]对MMC 直流侧双极短路故障进行了机理分析和公式推导,但MMC 双极短路故障下,毫秒级保护和几千安培的短路注入电流并不适用于故障穿越型直流变压器的设计。文献[15]针对MMC-ISOP 型电力电子变压器(PET)的中压母线短路故障隔离技术进行了探讨,其在200 μs 内实现故障阻断,但是并未详述混合串接的ISOP 型直流变压器的参数设计,更未涉及直流电抗器的设计原则。文献[16]探讨了直流变压器故障穿越方法,但是也未对涉及故障穿越性能的中压侧电抗的取值方法进行研究。文献[17-18]通过大量的仿真数据来确定限流电抗器电感,并未明确给出其计算方法。文献[19]给出了柔性直流输电(VSCHVDC)系统的直流电抗器电感设计方法,但是MMC闭锁后,交流系统侧依然会向短路点注入短路电流,并不能阻断短路电流的上升趋势,而纯直流系统不存在这样的问题,因此电感的设计原则与中压直流配电系统的直流变压器不同。
对于直流变压器而言,要求发生中压侧双极短路故障时注入系统的故障电流非常小(一般小于功率器件的额定电流),因此对闭锁时间要求苛刻,须要在更小的时间尺度下研究各可变参数之间的关系。本文基于改进ISOP 拓扑结构,根据当前直流配电网对中压直流故障穿越的特定要求,重点分析与故障穿越紧密相关的半桥和直流电抗器部分,分析中压侧双极短路故障(下文简称中压短路故障)下的电气特性,研究系统中各可变参数之间的关系;以中压侧直流电抗器电感为因变量,通过分析给出直流电抗器电感的计算方法;通过对隐式方程进行必要的简化推导出显式方程,从而更便于工程应用。
1 中压短路故障过程
与传统的ISOP 直流变压器相比,改进型ISOP直流变压器在前级串入了半桥和直流电抗器,因此在正常工作时,电流也会通过半桥和直流电抗器,如图1 所示。图中:n为改进型ISOP 直流变压器中串联子模块的总数;Qi1、Qi2(i=1,2,…,n)分别为子模块i的半桥上管、下管IGBT;Di1、Di2分别为Qi1、Qi2的反并联二极管;Ci1为子模块i的中压侧电容,记C为中压侧等效电容,则有C=(C11+C21+…+Cn1)/n;Ly为外置直流电抗器电感,Lx为线路等效电抗电感,记L为中压侧等效电抗器电感,则有L=Lx+Ly;R为整个短路回路的等效电阻;umv为中压侧直流母线电压。
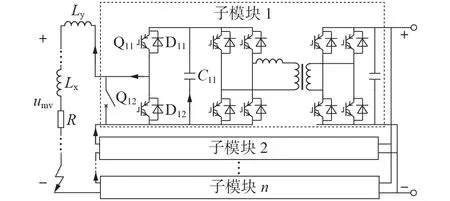
图1 改进型ISOP直流变压器及中压短路故障示意图Fig.1 Schematic diagram of improved ISOP type DCT and medium voltage short circuit
不同的算法对应不同的IGBT 控制方式,例如半桥控制算法只在发生故障时运行,正常工作时,全部的半桥上管Q11—Qn1导通,全部的半桥下管Q12—Qn2关断;采用移相脉冲宽度调制(PWM)控制算法时,半桥上管Q11—Q(n-2)1导通、Q(n-1)1—Qn1关断,对应地,半桥下管Q12—Q(n-2)2关断、Q(n-1)2—Qn2导通。但是无论采用何种控制方式,在稳定控制周期内半桥的总输出直流电压与直流母线电压接近,即保持为额定电压附近的平衡值,因此对分析中压短路故障过程基本不影响。为便于阐述和分析,本文假定所有子模块的半桥在正常工作时均为上管Q11—Qn1导通、下管Q12—Qn2关断,如图1所示。
改进型ISOP 直流变压器的中压短路故障过程与传统ISOP 直流变压器相同,分为C11—Cn1放电、D12—Dn2续流2 个阶段(分别记为阶段1、阶段2)。但2种直流变压器的阶段转换时刻不同,具体如图2所示。图中:t0为发生中压短路故障的时刻;t1为中压短路电流达到最大值Imax的时刻;t2为阶段1 转入阶段2的时刻;I2为t2时刻的中压短路电流;iL为中压短路电流;uC为中压侧等效电容电压。
为便于推导和说明,图2(a)、(b)中均假设中压侧直流母线的初始电流I0=0、初始电压为U0。t0时刻前,直流变压器正常工作,在t0时刻进入阶段1。对于传统ISOP 拓扑直流变压器,uC在t2时刻降低至0,被动进行状态切换。对于改进型ISOP 直流变压器,t2时刻uC并未降低至0,而是因半桥上管Q11—Qn1闭锁而主动进行状态切换。由图2 可知,I2为中压短路故障过程2 个阶段的共有参数,与故障穿越要求紧密相关,因此在探讨故障穿越相关问题时只需关注阶段1。对于改进型ISOP 直流变压器,由于Ly取值较大,一般满足R≪2L/C,因此R可忽略不计,令t0=0,则对应的微分方程为:
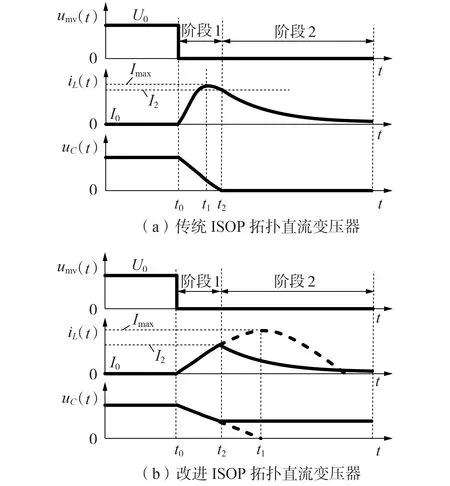
图2 发生中压短路故障时,2种直流变压器的参数变化Fig.2 Parameters change of two types of DCT under medium voltage short circuit
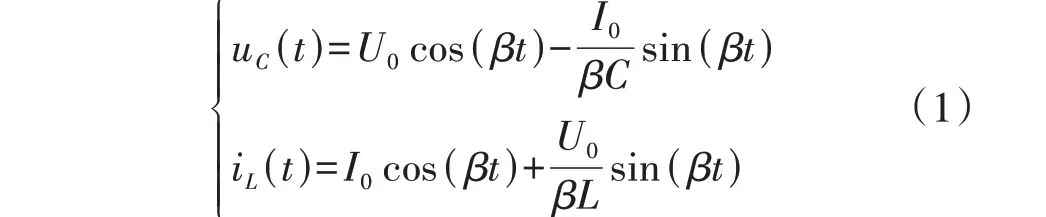
还可得:
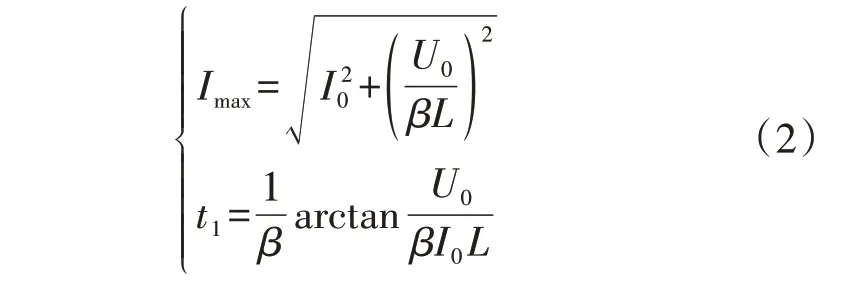
式中:β=1/
在I0=0 的情况下,iL会在1/4 的谐振周期达到最大值,但是半桥IGBT 的主动闭锁提前在iL的爬升过程中就阻断了其上升趋势,使得iL不会达到最大值,因此改进型ISOP 直流变压器的t2时刻会极大地超前t1时刻。
2 参数隐式关系式与显式关系式
2.1 参数隐式关系式
由于在直流变压器出口处发生中压短路故障时情况最恶劣,因此本文假定在改进型ISOP 直流变压器出口处发生中压短路故障,则L=Ly,由式(1)可得:
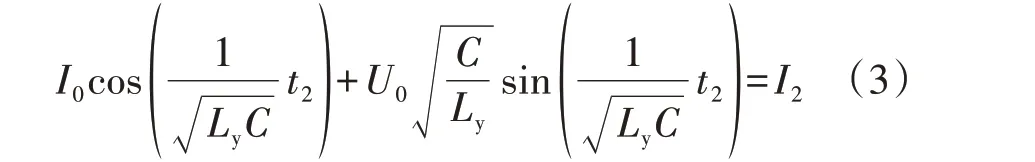
式(3)中,I2为设定值,即中压短路电流的最大允许值,其与故障穿越特性紧密相关,一般由系统规划设计方提出,设定为已知量。稳态下U0等于中压侧额定电压,系统参数确定后其一般是固定值,若有必要U0也可作为自变量进行研究。I0为额定值范围内的某个值,发生中压短路故障时并不会预先知道该值,因此I0也是一个自变量。C的取值同时受制于单级子模块的参数设计,可认为是一个有条件约束的自变量。t2一般受制于采样和控制电路的硬件参数,并不能无限制地小,因此也是一个有条件约束的自变量。与传统ISOP 直流变压器相比,改进型ISOP 直流变压器新增了外置直流电抗器,设计时主要考虑必须满足的故障穿越要求,需要考虑的其他因素不多,相对而言设计要求较为宽松,因此可将Ly作为因变量。由此可知,式(3)为一个含多变量的隐式非线性方程,不能直接求解Ly,只能利用相应的数学方法得到数值解[20]。假设C=220 μF,U0=20 kV,I2=450 A,则通过非线性求解可得到Ly、t2和I0之间的关系如图3所示。由图可见:t2越长,Ly越大,两者基本呈线性关系;对于特定的t2,当I0线性增大时,Ly并未随之呈线性增大的趋势。
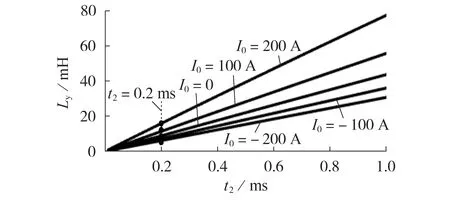
图3 Ly、t2和I0之间的关系示意图Fig.3 Schematic diagram of relationship among Ly,t2 and I0
当t2=0.2 ms 时,Ly和I0之间的关系如图4 所示。由图可见,随着I0的增加,所需的Ly越来越大,Ly呈现急剧上升趋势。由此可知,为了在一定时间内将中压短路电流限制在设定值,I0越大,需要的Ly就越大。类似地,C和U0对Ly的取值也有直接影响。
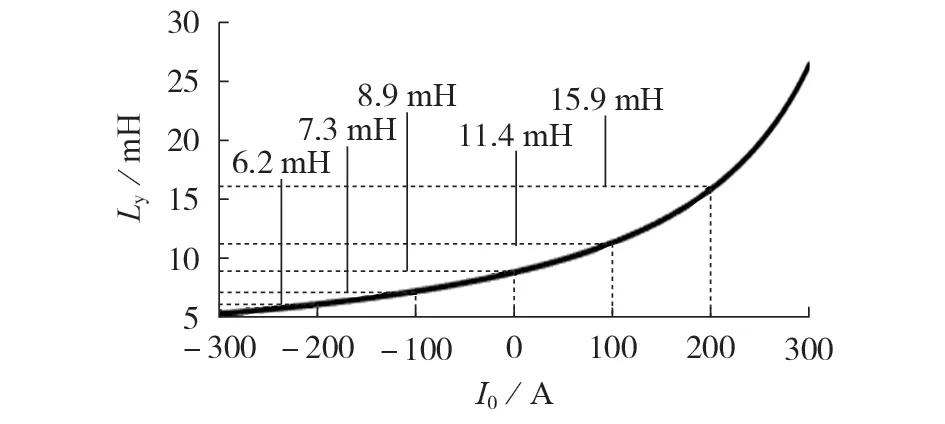
图4 当t2=0.2 ms时,Ly和I0之间的关系示意图Fig.4 Schematic diagram of relationship between Ly and I0 when t2=0.2 ms
Ly与其他参数的关系如附录A部分1)所示。
2.2 式(3)的显式表示
由于式(3)为隐式非线性方程,求解是通过数据计算工具计算得到数值解,从非线性方程本身较难看出各参数间的关系,且不便于工程应用。因此有必要对式(3)进行一定的改造,以求得其显式解。
根据正弦、余弦函数的泰勒展开式,当β t较小时,高阶分量较小,对正弦、余弦函数影响较小,可以忽略不计,则有:
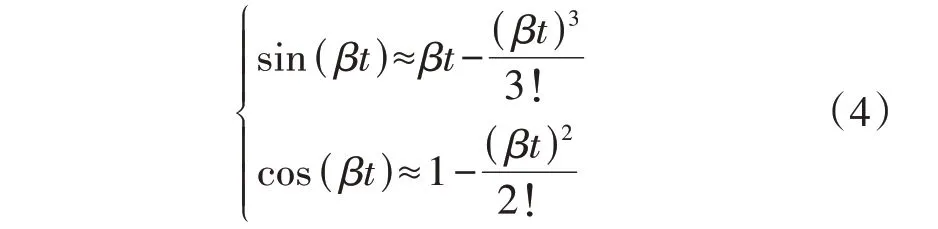
将式(4)代入式(3)后求解可得:
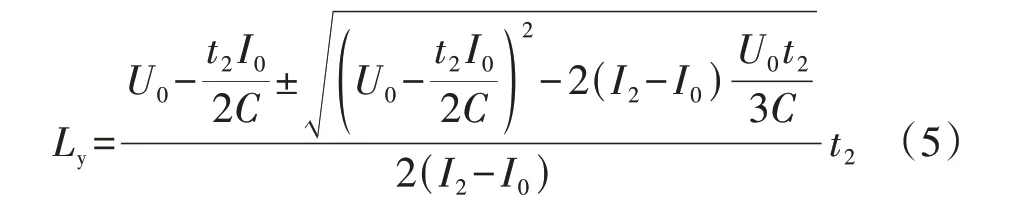
由式(5)可知,当C取值过小时有:
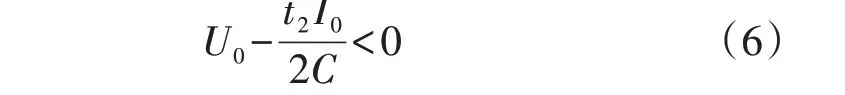
则无论式(5)中的“±”取“+”或“-”,均有Ly<0,导致无解。如果式(5)中的“±”号取“-”,则当C为无穷大时,Ly=0,该解也是无意义的。将按照式(5)获得的Ly值记为Ly2,则Ly2可确定为:
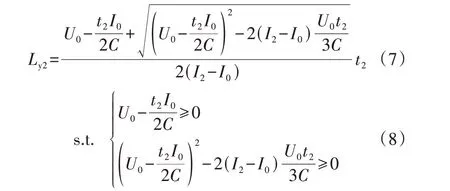
2.3 Ly2误差分析
定义Ly2与Ly的相对误差ΔL′y2=(Ly-Ly2)/Ly×100%。在I2=450 A、U0=20 kV、C=22 μF 的情况下,当t2∈[0.1,1]ms、I0∈[-200,200]A 时,ΔL′y2和t2、I0之间的关系如图5 所示。由图可见,在上述设定的t2、I0范围内,ΔL′y2曲面平滑无奇点,正向相对误差不超过5%,负向相对误差的绝对值不超过2%。
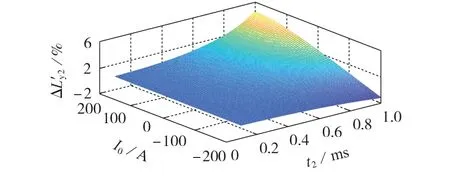
图5 ΔL′y2、t2、I0 之间的关系示意图Fig.5 Schematic diagram of relationship among ΔL′y2,t2 and I0
在I2=450 Α、I0=100 A、t2=0.2 ms 的情况下,当U0∈[5,50]kV、C∈[22,220]μF时,ΔL′y2、C、U0之间的关系如图6 所示。由图可见:在上述设定的U0、C范围内,正向相对误差不超过2%,无负向相对误差;相对误差较大的地方集中在U0和C取值较小的时刻,且有急速增大的趋势,只要U0或C取值稍大一些,相对误差就能大幅减小;当U0从5 kV 增大至10 kV 时,ΔL′y2从约2%减小为约0.3%;当C从22 μF增大至44 μF时,ΔL′y2从约2%减小为约0.3%。
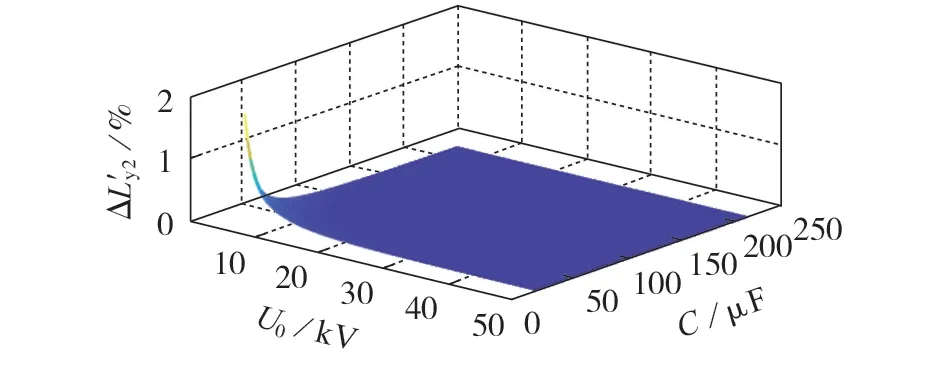
图6 ΔL′y2、C和U0之间的关系示意图Fig.6 Schematic diagram of relationship among ΔL′y2,C and U0
t2和I0的变化对Ly2等其他参数的影响如附录A部分2)所示。
3 式(7)的简化
3.1 约束条件下式(7)的简化
对于工程应用而言,式(7)依然较为繁琐,因此在一定条件下对其进行进一步的简化。令:
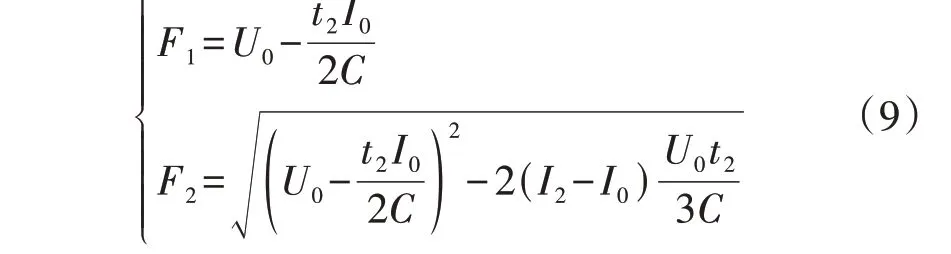
按照与式(7)的误差不超过10%的要求进行设计,可设定F1、F22的误差分别不超过5%、10%,即分别满足式(10)、(11)所示的条件。
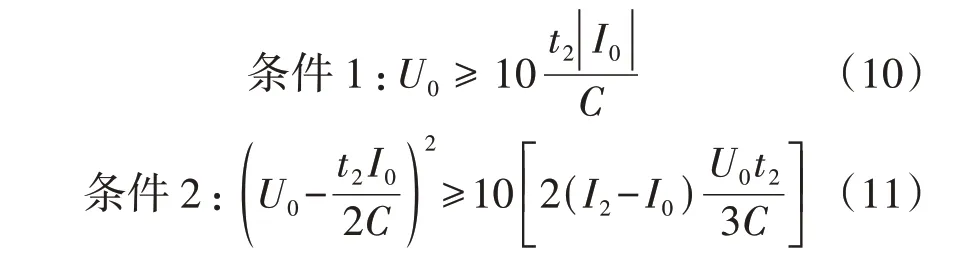
根据条件1对F1进行简化可得:
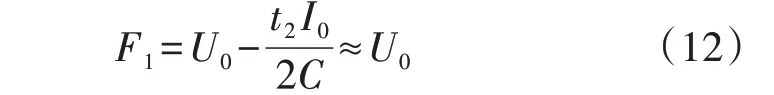
根据式(10)可知,F1简化前后的误差不超过5%。
根据条件2对F2进行简化可得:
根据式(11)、(13)可知,式(9)中F2的根号内的部分在简化前后的误差不超过10%,则开根号后所得F1与F2相比误差不超过5%。
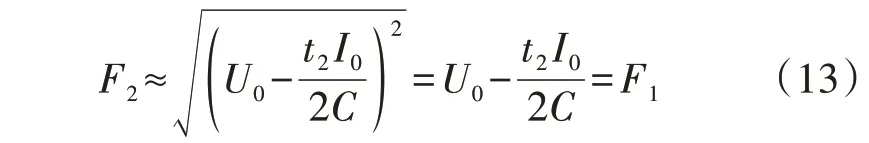
综上所述,从F1到U0经历1次简化,每次简化导致的误差不超过5%;从F2到U0经历2 次简化,每次简化导致的误差不超过5%。由此可知,F2简化为U0后,导致的误差不超过10%,则式(7)可进一步简化为式(10),简化前后的总误差不超过10%。则有:
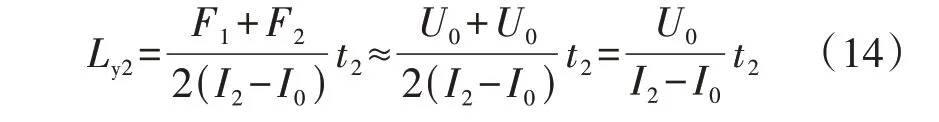
由于上述简化所使用的误差都是最大误差,实际上不一定在最大误差值处叠加,因此下文将根据实际参数取值范围进行进一步的误差核准。
将利用式(14)进一步简化后所得的Ly2值记为Ly3,则Ly3与其他参数的显式关系式总结如下:

3.2 Ly3误差分析
定义Ly3与Ly的相对误差=(Ly-Ly3)/Ly×100%。设定I2=450 A、U0=20 kV、C=44 μF,当t2∈[0.1,1]ms、I0∈[-200,200]A 时、t2、I0之间的关系如图7 所示,其为非平滑曲面,这是式(15)中不同条件对应不同的求解公式导致的。由图7 可见:在上述参数设定下,Ly3与Ly相差不大,<10%,满足设定的误差范围的最大值约为8%,位于突变的截面处,t2=0.45 ms、I0=200 A附近。
在I2=450 A、I0=350 A、t2=0.2 ms,U0∈[5,50]kV、C∈[22,220]μF 时、C、U0之间的关系见图8,其也为非平滑曲线。由图可见:在上述参数设置下,Ly3与Ly相差不大,小于10%,满足设定的误差范围;ΔL′y3的最大值约为6%,位于突变的截面处。
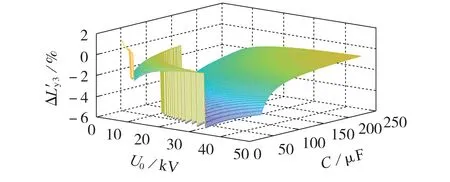
图8 、C和U0之间的关系示意图Fig.8 Schematic diagram of relationship among ,C and U0
综上所述,在设定的C、U0和t2、I0范围内,ΔL′y3均小于10%,满足设计要求。
参数t2和I0的变化对Ly3等其他参数的影响如附录A部分3)所示。
3.3 约束条件分析
3.1 节虽然在一定条件下对式(7)进行了简化,使得参数关系式相对简单,但实际上对应的约束条件并不直观。约束条件中包含U0、I2、I0、t2、C共5 个参数,在某个特定的工程中,U0、I2一般是事先就确定好的,因此可分析I0、t2、C这3个参数之间的关系。其中,I0为系统运行参数,t2、C由用户进行设置,因此将t2和C其中的1 个参数作为因变量,剩余的1 个参数和I0作为自变量,分析I0、t2、C间的关系。
设定U0=20 kV、I2=450 A,当t2∈[0.1,1]ms、I0∈[-300,300]A时,I0、t2、C间的关系如图9所示。
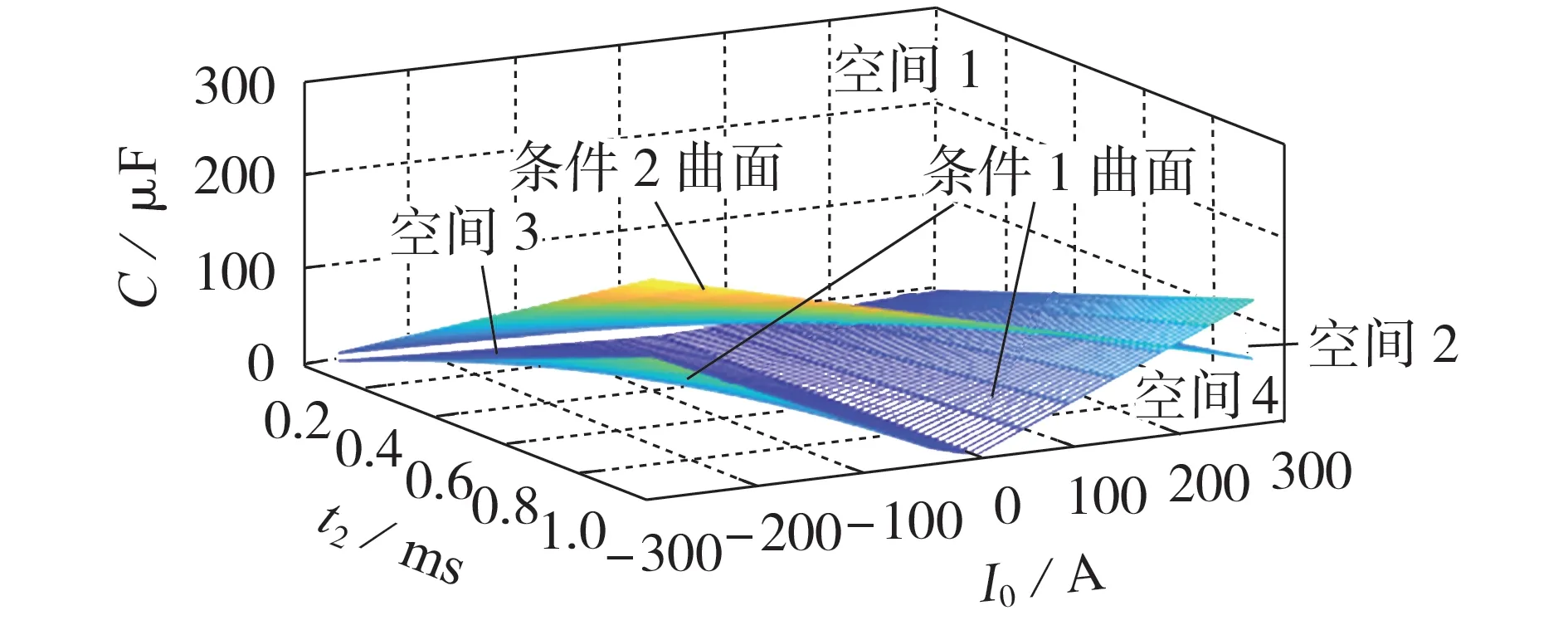
图9 I0、t2、C之间的关系示意图Fig.9 Schematic diagram of relationship among I0,t2 and C
由图9 可见:条件1 曲面关于I0=0 曲面呈镜面对称;在I0=200 A附近,条件1曲面、条件2曲面有一定的交叉,从而将空间分为4 个部分,高于2 个曲面的部分定义为空间1,高于条件2 曲面而低于条件1曲面的部分定义为空间2,高于条件1曲面而低于条件2 曲面的部分定义为空间3,低于2 个曲面的部分定义为空间4,这4个空间对应式(15)中从上至下的4 个约束条件;实际中,绝大多数情况位于空间1,相当一部分情况位于空间3、4,小部分情况位于空间2,可见实际情况下基本可通过简化公式进行计算。
随着I0逐渐减小,条件2曲面呈上升趋势;当I0<0 时,随着I0逐渐减小,条件1 曲面也呈上升趋势,故关注设定范围内I0最小值对应的曲面即可。
工程应用中t2仅受制于控保系统性能,一般不超过300 μs,其他参数的取值范围可参照2.3、3.2 节。即使在U0和C取最小值、I0取最大值时,式(16)也可被满足,则在实际工程应用中,式(16)基本都成立。
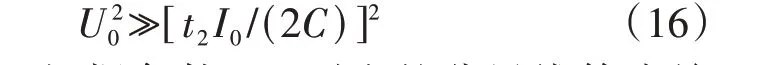
综上所述,根据条件1、2 列出的分界线等式关系分别如式(17)、(18)所示。
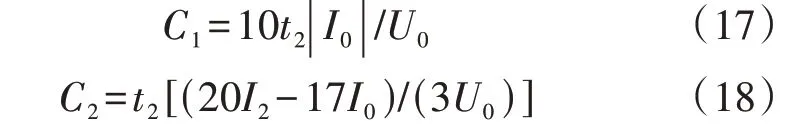
式中:C1、C2分别为条件1、2对应的C值。
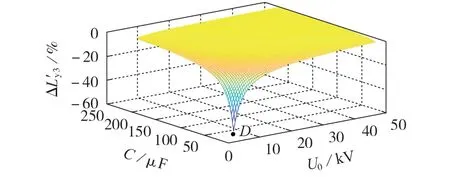
由于I0越小,C越大,因此设定I0=-100 A,将C作为因变量、t2作为自变量,绘制式(17)对应的C1曲线和式(18)对应的C2曲线,见图10。图中:区域1为同时高于2条曲线的部分;区域3为高于C1曲线而低于C2曲线的部分;区域4为低于2条曲线的部分。当I0<0 时,C1可能大于C2,也可能小于C2,而图10 对应C1 图10 C1曲线和C2曲线的示意图Fig.10 Schematic diagram of Curve C1 and C2 由此可知,可取控保系统能所达到的t2以及当前系统中C的交汇点,如图10 中虚线所示。如果交汇点落在区域1(例如点A),则采用式(15)中的第1个公式;如果交汇点落在区域3(例如点B),则采用式(15)中的第3 个公式。t2越小、C越大,交汇点越容易落到区域1。随着宽禁带半导体的应用和电力电子技术高频化的发展,对直流母线电容值的需求越来越小,交汇点会逐渐落入区域3。 传统计算方法将中压侧等效电容看成理想电压源,将中压短路故障过程看成对电感的线性充电过程,对应式(15)中的第1个公式,但是根据第3节的分析,式(15)中每个公式都是有约束条件的,否则会产生较大的误差。在图9对应的参数设置下,传统计算方法的ΔL′y3见图11。由图可见,传统计算方法的ΔL′y3在C变小时急剧变大,在点D(I2=450 A,I0=350 A,t2=0.2 ms,U0=5 kV,C=22 μF)处达到60%,对比图9可知,相同条件下式(15)的ΔL′y3只有约6%。 图11 与图9同等条件下,传统计算方法的Fig.11 of traditional calculation method under same conditions as in Fig.9 综上所述,根据式(15)中的约束条件,采用不同的简化公式,可以获得更为准确的结果。 以某工程实际参数为例,根据发生中压短路故障时各个参数之间的关系,利用式(15)快速给出直流电抗器电感的建议值。已知系统额定电流为100 A,电压初值U0=20 kV,双向功率传输。发生故障时短路电流越小,越有利于故障穿越,因此按照控保系统最快闭锁时间设置t2=160 μs,按照子模块工作需要的电容为3 000 μF 和中压侧30 级串联,可得到C=100 μF。由图10 可知,交汇点落在区域1 的中间位置,可采用式(15)中的第1 个公式直接进行计算,中压短路电流与闭锁时间呈线性关系。因此可用空载试验工况下的I2=350 A、I0=0,代替I2=450 A、I0=100 A,考虑到裕量50 A,实际取I2=300 A、I0=0,计算可得Ly3=10.66 mH。根据该计算值,实际中取Ly=10 mH,得到中压短路故障试验波形,见附录B 图B1。图B1 与图2(b)所示的过程对应,在闭锁时间160 μs 内,I2=300 A,与设计值一致,证明了本文所述直流电抗器电感简化计算方法的有效性。 本文讨论了在设计直流变压器中压短路故障穿越功能时,中压侧直流电抗器参数跟其他参数的关系,推导得到更直观的参数显式关系式,提出了在一定误差范围内适用于不同参数的简化方法。本文得到的主要结论如下: 1)若想得到较精确的各参数间的显式关系,则可采用式(7)直接进行参数计算,相对误差不超过±5%; 2)如果需要根据参数关系快速设计参数,则可以通过简化的式(15)及其约束条件进行计算,相对误差不超过±10%; 3)应注意工程用简化公式所带约束条件,闭锁时间越短,越容易满足其约束条件。 本文设置因变量为直流电抗器参数,同理可对任意其他参数进行类似推导。但是本文所述方法在实际工程应用时,还要结合其他因素的影响,例如电抗器过载时的线性度等,进行综合考虑。 附录见本刊网络版(http://www.epae.cn)。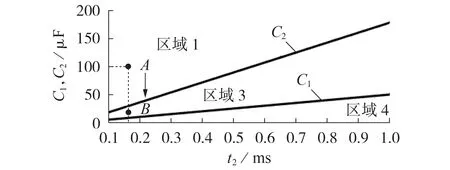
4 实验
5 结论
