双轴励磁发电机功率跟踪励磁控制系统研究

许国瑞，王珍珍，李伟力

（1. 华北电力大学 电气与电子工程学院，北京 102206；2. 北京交通大学 电气工程学院，北京 100044）

0 引言

随着单机容量的增加和特高压远距离输电的发展，同步发电机励磁电动势与系统电压的夹角越来越接近于极限值，降低了发电机及电力系统的稳定性。双轴励磁发电机（简称为双励机）转子上有d、q轴2套励磁绕组，可通过改变d、q轴励磁电流的比例调节励磁电动势的相位，从而提高电力系统的稳定性［1-2］。

理论和试验证明，双励机的稳态和暂态稳定性比普通发电机高［3-6］。20 世纪80 年代前苏联在世界上率先研制成功的2 台200 MW 双轴励磁汽轮发电机安装于乌克兰的布尔施登电厂，该厂曾经经历过一次系统稳定事故，导致8 台普通发电机全部停机，而这2台双励机却能够继续运行［7］。文献［8］以一台200 MW双励机接变压器双回线无穷大系统为例，计算了高压母线侧一回线首段发生三相短路故障，经过一定时间后切除故障线路的大扰动过程，结果表明双励机无论在发出无功还是吸收无功时均具有较高的暂态稳定极限。双励机之所以具有良好的调节特性和高稳定性，除了在转子上增加励磁绕组外，还必须有一套能充分发挥电机运行性能的励磁控制系统。因此，研究能够提高双励机稳定能力的励磁控制系统十分必要。

2003年，俄罗斯投运了型号为T3FA-110-2U3和T3FA-160-2U3、容量为110 MW 和160 MW 的全空冷双轴励磁汽轮发电机，其转子上具有2 套正交对称的励磁绕组，功率因数只能达到0.95；之后，俄罗斯又制造了型号为T3FAU-160-2U3 和T3FSU-320、容量为160 MW 和320 MW 双轴励磁汽轮发电机［9］，转子上具有2 套正交但不对称的励磁绕组，直轴为主绕组，交轴为控制绕组，控制绕组的磁动势占主绕组的7.5%～15%，功率因数可达0.85。西方工业发达国家的不少学者在20 世纪70 年代初期对双励机进行了原理性的探讨［10］。后来为了适应可再生能源发展的需要，其研究方向转向交流励磁水轮发电机、风力发电机领域，而针对双轴励磁汽轮发电机的研究没有取得明显进展。

双励机所采用的励磁控制方式大致分为分段控制、复式励磁控制、功能分离式控制、交流励磁控制和最优励磁控制［11］。目前采用较多的励磁控制方法是双通道励磁控制，属于功能分离式控制，其具有的有功通道和无功通道可以实现有功和无功功率的独立调节，更有利于电机的稳定运行［12］，这也是优于其他励磁控制策略之处。文献［13］详细介绍了双通道励磁控制系统以及各控制变量的作用；文献［14］通过讨论双通道励磁控制系统中各控制系数与双通道控制闭环特征根、响应特征的关系确定了各控制系数的值；文献［15］改进了双励机的控制方法，建立了动态同步轴系下的双通道励磁控制系统，进一步缩短了双励机的动态过程。对于通过提高双励机的阻尼来改善动态过程尚未有相关研究。

目前，我国已基本形成了“强直弱交”的特高压交直流混联电网格局，但是交流电网在整个系统中依然发挥着基础性支撑作用，其稳定性直接影响电网的连续可靠性供电。双励机励磁磁动势方向的可调节性使得转子位置角和功角相互独立，克服了传统同步发电机稳定运行能力受功角极限限制的缺点，能够显著增加交流电网的稳定性，为我国高可靠性坚强电网的建设提供必要的技术支持［16］。

本文在双通道励磁控制系统的基础上，提出基于功率跟踪的双励机励磁控制系统。首先，介绍了双励机双通道励磁控制系统的控制方法及控制变量；在此基础上，通过对有功功率、无功功率和励磁电流差值进行不完全微分，推导了基于不完全微分控制的功率跟踪励磁控制系统；最后，以转矩扰动和无功扰动为例，对比研究了功率跟踪控制系统与双通道励磁控制系统对双励机动态过程振荡时间和振荡幅值的影响。研究结果可为提高电力系统稳定性提供有力支撑。

1 双励机的双通道励磁控制系统

1.1 双励机的数学模型

本文采用dq0坐标下的双励机模型，包括3阶定子绕组方程、2 阶励磁绕组方程和2 阶阻尼绕组方程。采用xad基值系统，建立双励机在dq0 坐标系下基本方程的标幺值形式如下［17］：

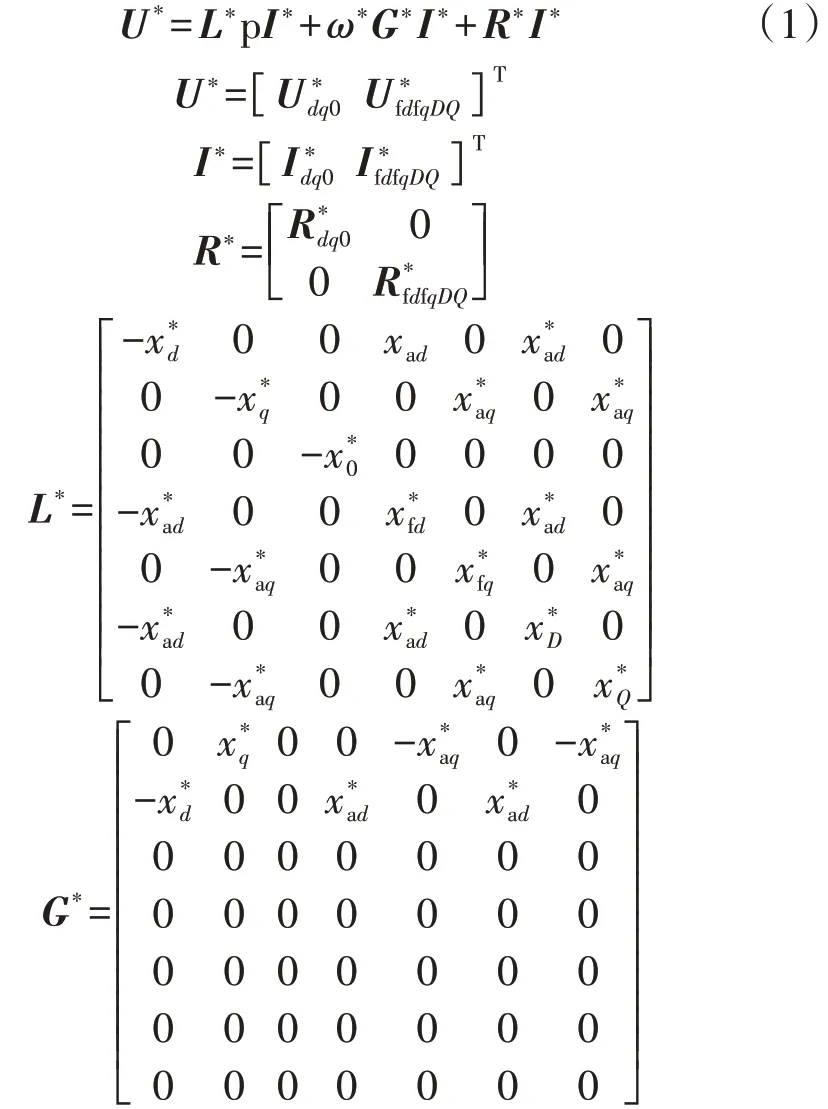
式中：ω为转子角速度；xd和xq、xfd和xfq、xD和xQ分别为直轴和交轴同步电抗、励磁绕组电抗、阻尼绕组电抗；xad、xaq分别为直轴、交轴电枢反应电抗；Udq0、UfdfqDQ分别为定子dq0 绕组、直交轴励磁绕组和阻尼绕组的端电压；Idq0、IfdfqDQ分别为定子dq0 绕组、直交轴励磁绕组和阻尼绕组的电流；Rdq0、RfdfqDQ分别为定子dq0 绕组、直交轴励磁绕组和阻尼绕组的电阻；“*”表示相应变量的标幺值。

1.2 双通道励磁控制系统的数学模型

双励机的定子结构与普通同步发电机相同；两者的区别主要在于转子结构，普通同步发电机的转子上只有1套励磁绕组，而双励机的转子上具有2套励磁绕组，绕组轴线相差90°或60°机械角度，这使双励机具有普通同步发电机无法比拟的优点［1］，即双励机励磁磁动势的相位可与转子位置角解耦控制。

为了发挥双励机的优点，文献［8］提出了双通道励磁控制策略。图1 为双励机双通道励磁控制器的框图，通过有功通道和无功通道分别控制励磁电流在q、d轴上的投影从而实现对有功功率和无功功率的独立调节。有功通道的主要功能是控制与发电机有功相关的物理量，即有功功率、转子位置角、转差率和励磁电流偏差，保证发电机转子机械运动的稳定性和有功功率的输出。无功通道的主要功能是以发电机端电压或无功状态为反馈量进行相关计算，从而达到控制发电机端电压或无功运行状态的目的［8］。

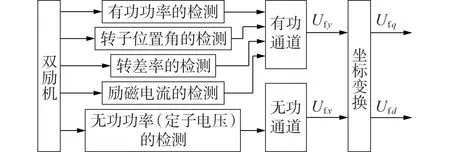
图1 双励机的双通道励磁控制框图Fig.1 Block diagram of dual-channel excitation control for DESG

根据图1 可以写出双通道励磁控制系统的控制方程为［8］：

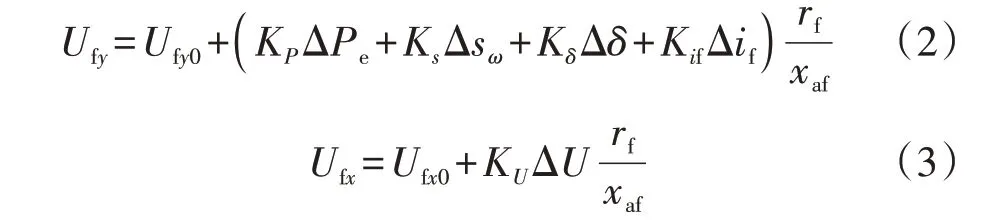
或

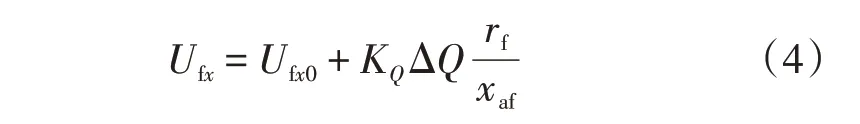
式中：Δif=ifq-ifd；ΔPe=Pe-Pe0；Δsω=sω-sω0；Δδ=δ-δ0；ΔU=Ut-U0；ΔQ=Qt-Q0；KP、Ks、Kδ、Kif、KU和KQ分别为ΔPe、Δsω、Δδ、Δif、ΔU和ΔQ的比例系数；rf/xaf为将励磁电压以额定空载励磁电势为基值归算到定子侧的系数；ifd、ifq、Pe、sω和δ分别为双励机的d轴励磁电流、q轴励磁电流、有功功率、转差率和转子位置角；U0、Q0、sω0、Pe0均为给定值；δ0为前一运行状态的转子位置角；Ufy0、Ufx0为前一状态的计算值；Ufy、Ufx分别为控制系统计算得到的y、x轴励磁电压；Ut为双励机的机端电压，Qt为双励机机端输出的无功功率。

2 功率跟踪励磁控制系统

2.1 不完全微分控制

比例控制着眼于当前数据，微分控制则能预测数据的变化趋势，具有预测作用。比例微分控制器的传递函数为：

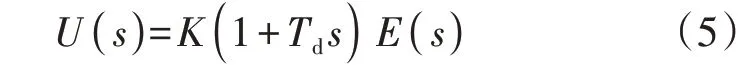
式中：U(s)为输出变量；E(s)为输入变量；K为比例系数；Td为微分时间常数。微分控制部分的传递函数为：

令m=KTd，则式（6）变为：

其后向差分的离散方程为：

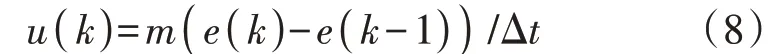
式中：k为采样次数；e为输入的误差信号；u为e的微分；Δt为采样周期。

由式（8）可以看出，微分控制通过对输入误差求导可以预测误差的变化，进而跟踪变量的变化趋势。微分控制器的预测作用可以产生超前的控制作用，该作用可为系统引入一个超前的修正信号，抑制被调量的振荡，即增加了系统的阻尼作用。因此，微分控制可以减小超调量，减少调节时间，增强系统稳定性。

比例控制器的控制作用在偏差产生后才开始，很难控制具有较大惯性的系统，而双励机就是一个具有很大惯性环节的系统。在比例控制器中加入微分控制，比例部分反映偏差的大小，微分部分在偏差刚产生时，通过对偏差的趋势进行判别，进一步控制系统来消除偏差，增加系统阻尼，减小超调量，减少调节时间，使系统快速稳定［18］。

微分控制可以改善系统控制效果，增加系统稳定性，但微分作用会把高频干扰放大，使系统对干扰的抑制能力减弱。当瞬时误差变化较大时，微分作用的输出会急剧增加，易引起控制过程的振荡，反而会使得控制效果变差。普通微分作用只在第一个周期内起作用，不能按照偏差变化的趋势在整个调节过程中起作用，因此仅在第一个周期内的微分作用很强，对于时间常数较大的系统，其在整个调节过程中的调节作用很小，不能达到超前控制误差的目的。为了克服上述缺点，避免纯微分环节出现在控制器中，可以在微分项上串联一个一阶惯性环节1/(1 +Tds/Kd)，其中Kd为不完全微分因子，则纯微分变成了不完全微分［19］。

本文的功率跟踪控制系统中，只采用比例微分控制，而不采用积分控制。在式（5）的微分项上串联一阶惯性环节1/(1 +Tds/Kd)，则本文最终采用的不完全微分控制的传递函数为：

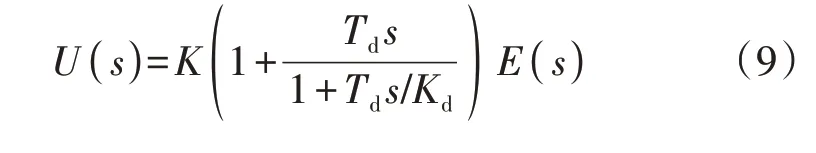
令：

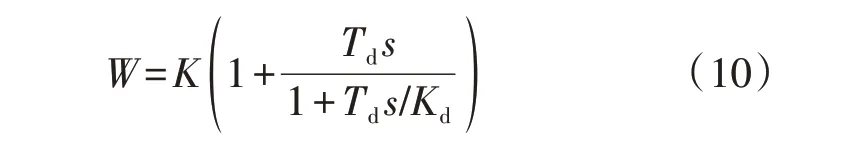
则式（9）中不完全微分控制部分的传递函数为：

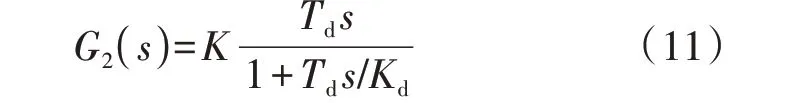
令n=Td/Kd，则式（11）可写成：

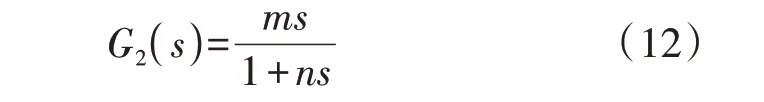
其后向差分的离散方程为：

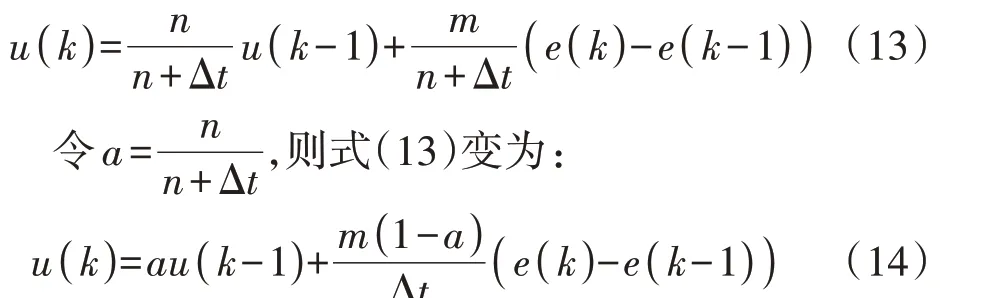
对比式（14）和式（8）可以看出：一方面，不完全微分比纯微分多了一项au(k-1)，该项表示不完全微分具有积分功能，这是由于串联的一阶惯性环节属于相位滞后环节，具有积分功能，而积分功能对高频干扰有滤波作用；另一方面，微分项的系数由原来的m减小到m(1-a)，即当输入信号为阶跃信号时，微分控制的输出在第一个采样周期内的脉冲高度下降，此后按指数规律衰减，微分作用逐渐减弱，不易引起振荡，且由于微分项输出幅度小，因而作用时间长，能在各个采样时间周期内起到微分作用。因此，不完全微分增强了对高频干扰的抑制能力，且不引起控制过程的振荡，其微分作用可以在整个调节过程中按照误差的变化趋势均匀地输出，真正意义上起到了微分的作用［20］。

有功功率、无功功率和机端电压对时间的不完全微分分别为：

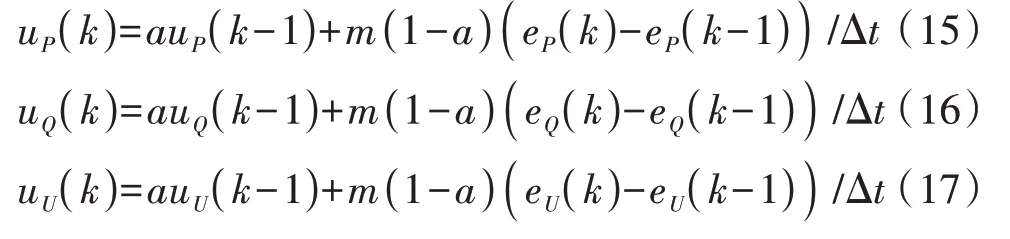
式中：下标P、Q和U分别对应有功功率、无功功率和机端电压。

通过式（15）—（17）分别对双励机的有功功率、无功功率和电压的误差进行不完全微分运算，通过对其变化趋势的预测，实现超前控制，达到提高系统阻尼、减小振荡幅值和振荡时间的效果。

2.2 功率跟踪控制系统的模型

在双通道控制系统的模型中引入了多个变量的反馈环节，在所有变量的反馈中，均采用比例控制。多个变量的反馈中，各反馈系数之间的相互配合给整个建模过程带来很大麻烦。其中，转子位置角和转差率的反馈是为了保证电机的稳定运行，缩短电机的动态过程，改善电机的动态特性。而不完全微分控制器可以减小系统超调量，使系统快速稳定，改善控制效果。

因此本文将转子位置角和转差率反馈省去，在剩余反馈变量有功功率、励磁电流差值和无功功率或机端电压的控制器中引入不完全微分控制，以改善电机的动态性能，构成的功率跟踪控制系统模型如式（18）—（20）所示。

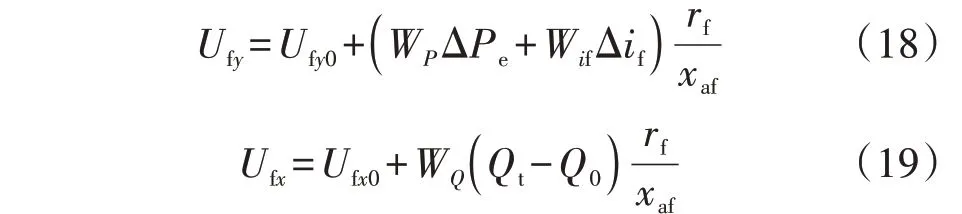
或

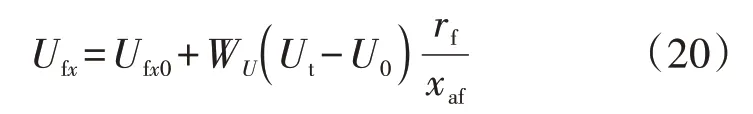
式中：WP、WQ、Wif、WU可根据式（10）得到，相应地将K、Td、Kd分别修改为KP、TdP、KdP，KQ、TdQ、KdQ，Kif、Tdif、Kdif和KU、TdU、KdU即可，KP、TdP、KdP分别为有功功率控制器的比例系数、微分时间常数和不完全微分因子，Kif、Tdif、Kdif分别为励磁电流控制器的比例系数、微分时间常数和不完全微分因子，KQ、TdQ、KdQ分别为无功功率控制器的比例系数、微分时间常数和不完全微分因子，KU、TdU、KdU分别为机端电压控制器的比例系数、微分时间常数和不完全微分因子。

图2 为采用有功功率、励磁电流差值和无功功率反馈时的双励机功率跟踪控制系统的传递函数框图。

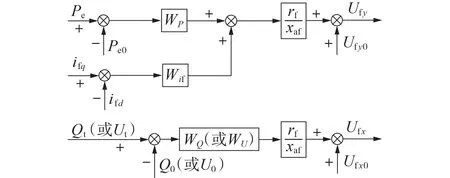
图2 功率跟踪控制系统的传递函数框图Fig.2 Block diagram of transfer function of power tracking control system

2.3 反馈系数的确定

根据文献［8］对反馈系数取值范围的推导，得到各比例系数取值为：

在不完全微分控制器中，用于消除当前误差的是比例部分，微分部分的作用在于对动态性能的改善，所以比例系数的选取更为重要，微分时间常数和不完全微分因子的选取只要满足对系统动态性能的要求即可。所以在整定各反馈系数时，先利用式（21）确定各比例系数；在确定各不完全微分因子Kd和微分时间常数Td时，利用试凑法，先确定一个Kd值，Kd一般取2～10 就可以达到很好的控制效果，之后逐渐增大Td，使得微分作用逐渐增强，观察其响应速度，并多次改变Kd值，找到合适的Kd值和Td值，以使系统达到理想效果。

传统双通道励磁控制系统中有功功率、无功功率、转子位置角和转差率的反馈系数之间的相互配合对动态性能的影响很大，因此整定过程很复杂。而功率跟踪控制系统仅需要考虑有功功率和无功功率反馈系数中比例系数的配合，微分时间常数和不完全微分因子只需要根据各不完全微分控制器中比例系数的值进行选取，达到动态性能要求即可，反馈系数的整定过程更简单。

3 仿真计算

利用双励机的Park 方程建立其仿真模型，并与无穷大系统模型相连。所采用的300 MW 双励机d、q轴参数对称，其中各d轴参数如附录A 表A1 所示。根据式（18）、（19）建立功率跟踪控制系统的仿真模型，根据式（2）、（4）建立传统双通道励磁控制系统的仿真模型，对2 种控制系统的控制效果进行对比。仿真时，2种系统中取相同的比例系数。

3.1 转矩扰动对比

当双励机运行在迟相工况时，保持无功功率不变，在t=0.2 s 时，拖动转矩从0.86 p.u.阶跃变化到0.70 p.u.后，双励机的机端电压Ut、有功功率Pt和无功功率Qt的变化曲线如图3所示（Ut、Pt和Qt均为标幺值，后同）。从图中可以看出：2 种励磁控制方式下，双励机的机端电压均可恢复稳定且变化幅度较小；采用功率跟踪励磁控制后，功率的振荡幅值和振荡时间明显减小，机端电压恢复更快。表1给出了5种特性指标的对比。表中：Pflu、Qflu分别为有功、无功振荡幅值（标幺值，后同）；TP、TQ分别为有功、无功振荡时间；TU为机端电压恢复时间。从表1可以看出，采用功率跟踪励磁控制系统后，有功、无功振荡幅值分别只有双通道励磁控制系统的约9.1%和7.5%，有功、无功振荡时间分别减少了1.09 s 和0.60 s，机端电压恢复时间减少了0.81 s。

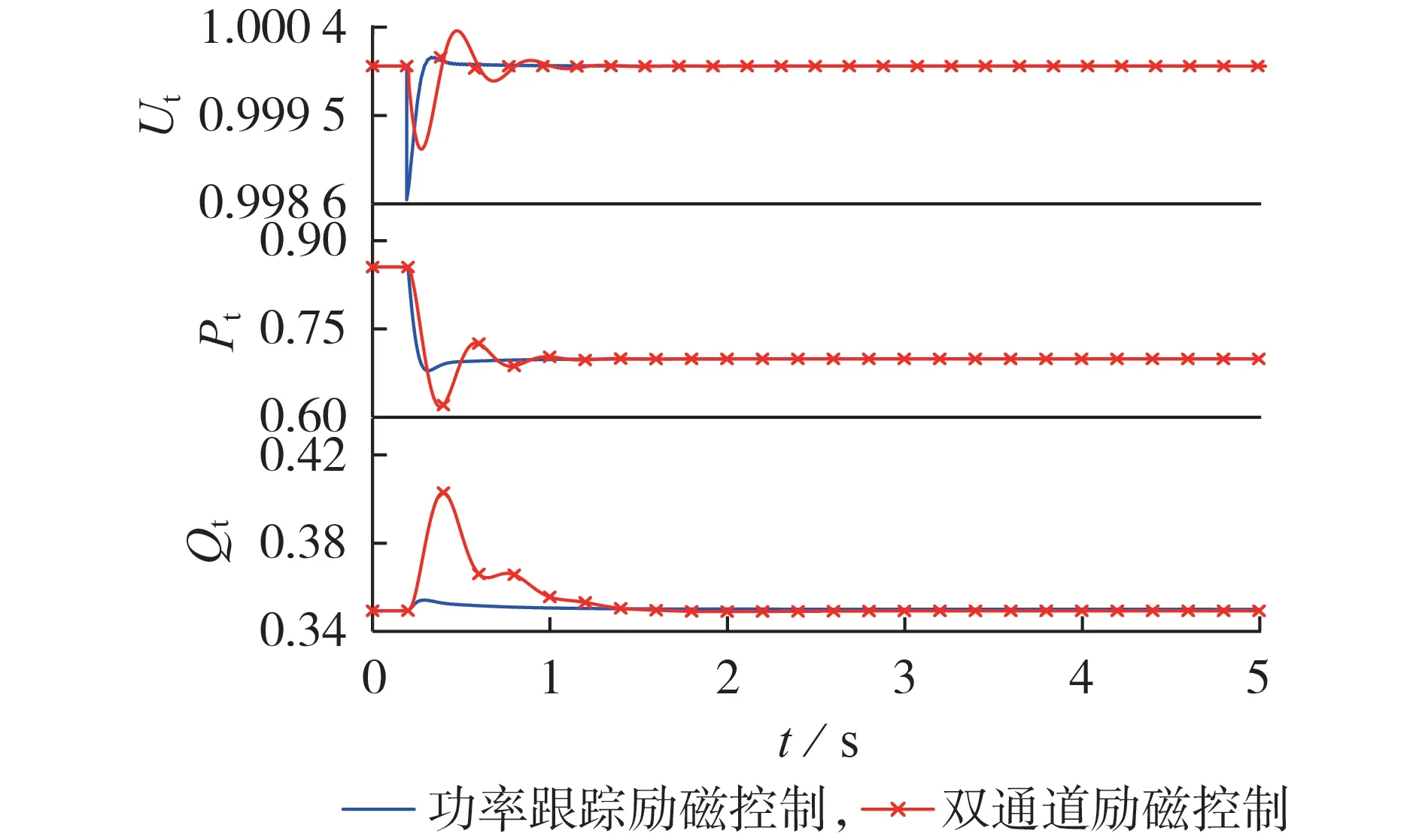
图3 迟相运行时施加转矩扰动的仿真结果Fig.3 Simulative results under torque disturbance during late phase operation

表1 迟相运行时施加转矩扰动的特性指标对比Table 1 Comparison of performance indexes under torque disturbance during late phase operation

当双励机运行在进相工况时，双励机的机端电压、有功功率和无功功率的变化曲线见附录A 图A1。从图中可以看出：2 种励磁控制方式下，双励机的机端电压均可恢复稳定且变化幅度较小；采用功率跟踪励磁控制后，功率的振荡幅值和振荡时间明显减小，机端电压恢复更快。附录A 表A2 给出了5种特性指标的对比。从表中可以看出，采用功率跟踪励磁控制系统后，有功、无功振荡幅值分别只有双通道励磁控制系统的约35.3%和85.7%，有功、无功振荡时间分别减少了1.87 s 和1.44 s，机端电压恢复时间减少了1.99 s。

3.2 无功扰动对比

当双励机运行在迟相工况时，保持有功功率不变，t=0.2 s时无功功率从0.35 p.u.阶跃变到-0.35 p.u.，双励机的机端电压、有功功率和无功功率的变化曲线见图4。从图中可以看出：2种励磁控制方式下，双励机的机端电压变化幅度均较小；采用功率跟踪励磁控制后，功率的振荡幅值和振荡时间明显减小，机端电压恢复更快。表2给出了5种特性指标的对比。从表中可以看出，采用功率跟踪励磁控制系统后，有功、无功振荡幅值分别只有双通道励磁控制系统的约83.3%和50.0%，有功、无功振荡时间分别减少了0.90 s和2.12 s，机端电压恢复时间减少了1.71 s。

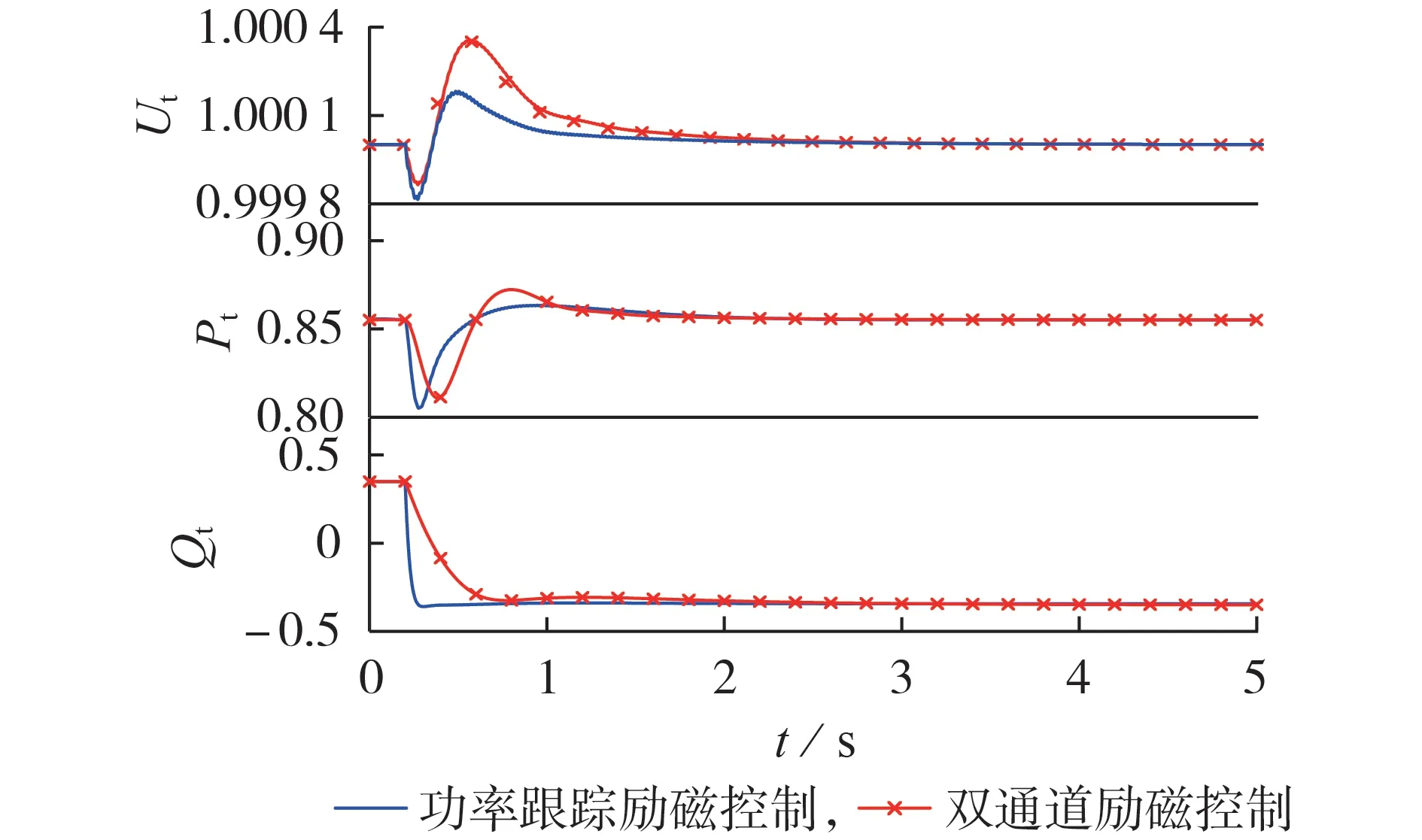
图4 迟相运行时施加无功扰动的仿真结果Fig.4 Simulative results under reactive power disturbance during late phase operation

当双励机运行在进相工况时，双励机的机端电压、有功功率和无功功率的变化曲线见附录A 图A2。从图中可以看出：2 种励磁控制方式下，双励机的机端电压变化幅度均较小；采用功率跟踪励磁控制后，功率的振荡幅值和振荡时间明显减小，机端电压恢复更快。附录A 表A3 给出了5 种特性指标的对比。从表中可以看出：采用功率跟踪励磁控制系统后，有功振荡幅值和双通道励磁控制系统几乎相等，但有功振荡时间减少了1.47 s；无功振荡幅值只有双通道励磁控制系统的50.0%，无功振荡时间减少了1.02 s；机端电压恢复时间减少了0.36 s。

3.3 系统电压阶跃响应对比

计算了双励机在迟相和进相2 种运行工况下，系统电压突升5%后的动态响应特性，结果如图5所示。从图中可以看出，采用功率跟踪励磁控制后，机端电压可以更快恢复稳定。表3 给出了不同工况下的机端电压恢复时间。从表中可以看出，与双通道励磁控制系统相比，采用功率跟踪控制系统后，迟相和进相运行工况下双励机的机端电压恢复时间分别减小了1.77 s和5.85 s。

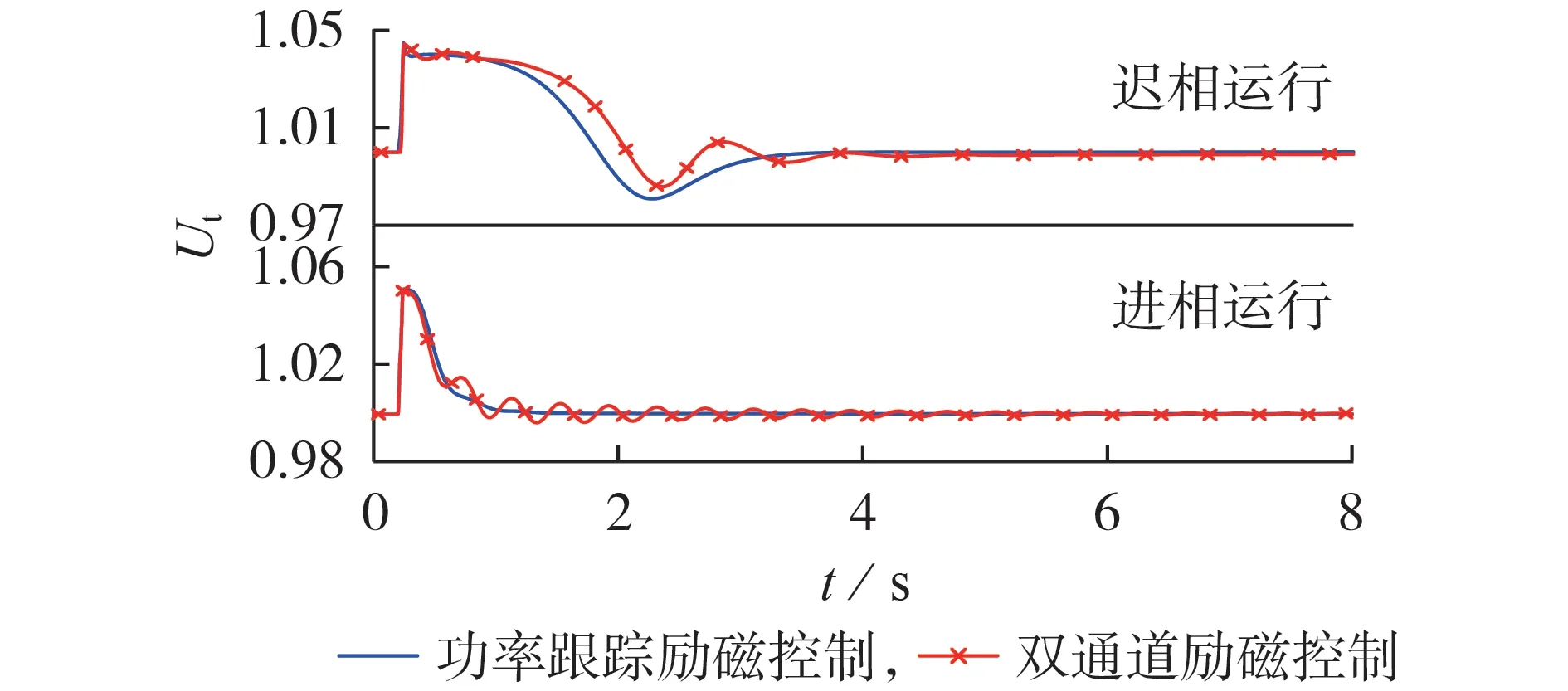
图5 机端电压波形对比Fig.5 Comparison of terminal voltage waveforms

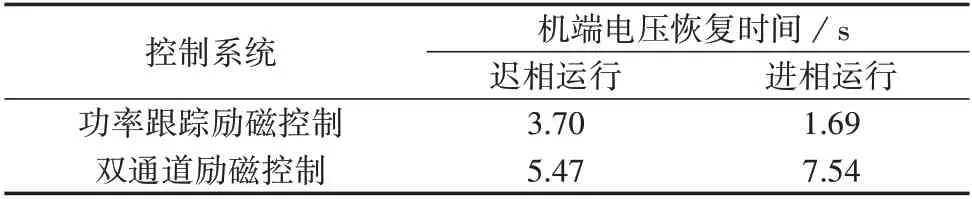
表3 机端电压恢复时间对比Table 3 Comparison of terminal voltage recovery time

从对比结果可以看出：功率跟踪励磁控制系统可以实现双励机有功和无功的独立调节；施加转矩扰动和无功扰动时，功率跟踪励磁控制系统的有功和无功振荡幅值更小、振荡时间更短，机端电压的恢复时间更短，响应速度更快，可以更快地恢复稳定，动态性能更好；系统电压阶跃变化时，采用功率跟踪励磁控制系统后，双励机的机端电压能更快恢复稳定。

4 结论

本文提出了一种具有功率跟踪功能的双励机功率跟踪励磁控制系统。在转矩扰动、无功扰动和系统电压扰动情况下，对功率跟踪励磁控制系统和双通道励磁控制系统的动态性能进行了对比研究。结果表明，与传统的双通道励磁控制系统相比，功率跟踪励磁控制系统减小了动态过程中系统的功率振荡幅值和振荡时间，缩短了调节时间，能获得更好的动态性能，为电力系统的稳定运行提供有力支持。除此之外，功率跟踪励磁控制系统的反馈变量数量少，反馈系数之间的配合更简单，反馈系数值更易选取。

附录见本刊网络版（http：//www.epae.cn）。