计及分布参数的双端口等效牵引网建模、验证及稳定性分析

陈浔俊，李国荣，刘志刚，邓云川

（1. 西南交通大学 电气工程学院，四川 成都 611756；2. 中铁二院工程集团有限责任公司，四川 成都 610031）

0 引言

牵引网系统是一个由多条传输导线组成的分布参数网络系统，在其沿线的各导线的每一单元长度均存在电阻、电感、对地电容和漏电导，并且未加屏蔽层的各导线之间还存在互电感和互电容［1］。对于牵引网模型，我国早期的基础研究一般将其视为单相均匀输电线，根据电力机车所处线路位置对其所在供电臂进行分段处理，同时，借用电力系统分析的方法，只考虑牵引网线路两侧端口的电压和电流，将每段视作一个二端口网络进行处理，用单相π 型等值电路表征牵引网的端口特性。此外，牵引网的多级π型等值电路是由多个π型等值电路并联而成，π型等值电路的数量越接近无限大，多级π 型等值电路模型的仿真结果越接近分布参数模型［2］。

需要注意的是，上述集总参数等效模型在电路中的电场和磁场默认是相互独立的，电能的传输过程是在瞬间完成的，即该电路中的元件任意端口的瞬时电流和瞬时电压是完全确定的，与元件的实际空间位置无关［2］。因此，该模型中的元件参数和元件所在位置无关，所以集总参数不能反映牵引网分布参数特性［3］。

国内外关于基于多导体传输理论的链式网络模型的研究取得了较多成果。文献［4］基于不同供电方式对牵引网搭建复合链式模型，按照链式电路的拓扑结构，利用牵引网各元器件的节点导纳矩阵构建出较为精确的数学模型。文献［5-6］结合牵引网多导体传输特性，研究圆导线阻抗计算方法以及钢轨对地漏电导，采用π 型等值电路模拟牵引网的复杂拓扑结构。文献［7］以多导体传输线模型为基础，构建适用于不同供电方式的牵引网通用数学模型，在链式网络结构的基础上，建立交流牵引供电系统的仿真通用数学模型。目前，牵引网普遍采用的供电方式为全并联AT供电方式，该供电方式下的牵引网结构复杂，包括上（下）行接触线T、承力索、正馈线F、钢轨R、保护线PW 和贯通地线G 等10 余条线路［8］。同时，在该供电方式下建立的牵引网模型大多采用链式电路模型，将上述多根供电导线看作一个多导体 传 输 线MTL（Multi-Transmission Line）电 路 模型［9］，利用链式多导体理论对牵引网进行建模。在理论分析和仿真计算中，若对各导线单独考虑，则导线数目较多，计算困难［7］，不利于建立高速铁路耦合系统的阻抗模型，进行系统层级的稳定性分析研究。

综上所述：牵引网π 型等值电路模型简单，计算方便，但不能反映牵引网的分布特性；牵引网链式模型建模精确，计算结果准确，但建模与计算复杂，构建的模型阶数庞大，难以适用于基于阻抗的级联系统稳定性分析，同时也难以得到牵引网自身的阻抗解析解。此外，考虑到牵引网系统只存在无源元件，作为线性系统，其阻抗特性在低频处主要呈现感性，在高频处，对于牵引网的开路导纳和短路导纳，其阻抗特性在感性和容性之间跳变，存在多个谐振尖峰，可能导致系统振荡现象。因此，针对上述问题，本文结合链式模型分布参数特性和π 型等值电路的优点，通过一次测量得到线路的分布参数，基于双端口网络理论建立牵引网等效模型，该模型简化了传统牵引网需要按照单位长度多次测量计算的步骤，降低了以往多导体传输线模型建模的复杂程度，解决了多导体链式模型难以直接用于基于阻抗分析的级联系统稳定性分析的问题。

本文主要内容如下：首先，采用一种基于双端口网络理论的等效方法，建立计及分布参数特性的解耦的双端口牵引网模型；然后，对得到的牵引网模型进行理论和实际测量数据的阻抗验证；最后，将建立的等效牵引网模型应用到车网系统稳定性分析中，针对不同的牵引网条件，在MATLAB／Simulink 仿真平台上进行分析验证，证明了所建立双端口牵引网模型能用于高速铁路车网耦合系统的阻抗分析。

1 牵引网双端口等效电路建模

目前，关于长距离牵引网传输线路的研究大多是采用全并联AT 供电方式的链式模型或者多级π型等值电路，而不是将其建模为诺顿-戴维南等效电路［10-12］。结合现阶段的研究，本文尝试采用一种解耦的长距离双端口等值电路模型来表征电力电缆的端口特性。与传统牵引网电路模型相比，解耦的双端口电路模型在保留其分布参数特性的同时，也使得后续级联系统的稳定性分析更加直观。多级π 型牵引网模型原理图如图1所示，图中多级π型等值电路由m个π 型等值电路并联而成，每一级的单位长度相同，均为Δl，u1、i1分别为输入端口电压、电流，u′、i′分别为输出端口电压、电流。1 个微分段的牵引网分布参数模型示意图如图2 所示，图中u、i分别为输入端口电压、电流。分布参数包含牵引网的单位长度电阻R0、单位长度电感L0、单位长度电容C0、传播系数γ以及特征阻抗Zc，x为空间距离。

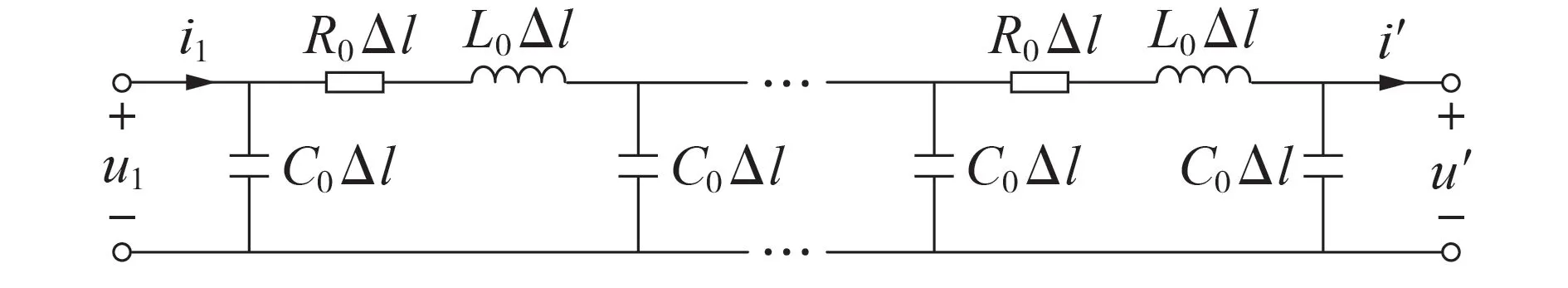
图1 多级π型牵引网模型原理图Fig.1 Principle diagram of multi-level π-type traction network model

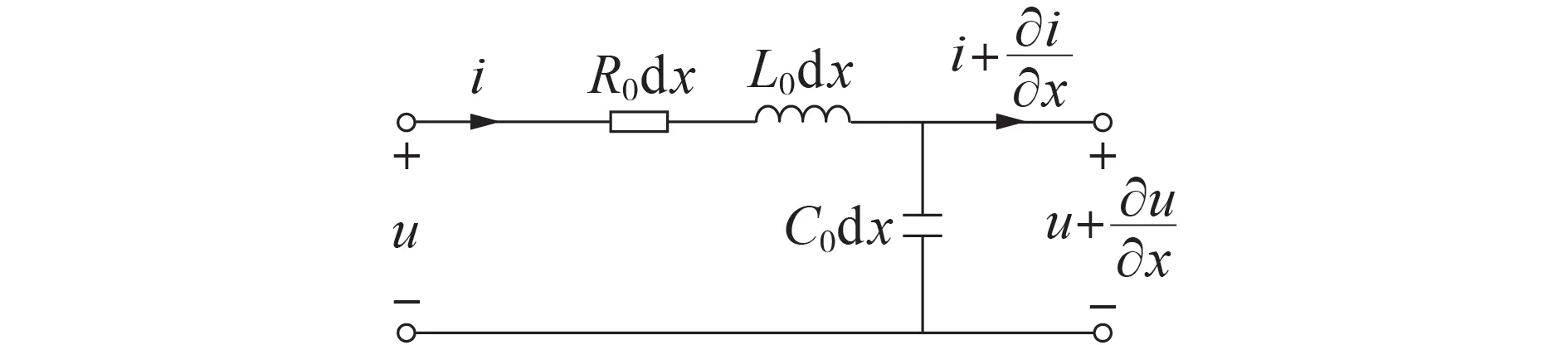
图2 1个微分段的牵引网分布参数模型示意图Fig.2 Schematic diagram of distribution parameter model of traction network with a differential segment

对于图2所示模型，牵引网传播系数γ以及牵引网的特征阻抗Zc与单位分布参数具有如下关系：

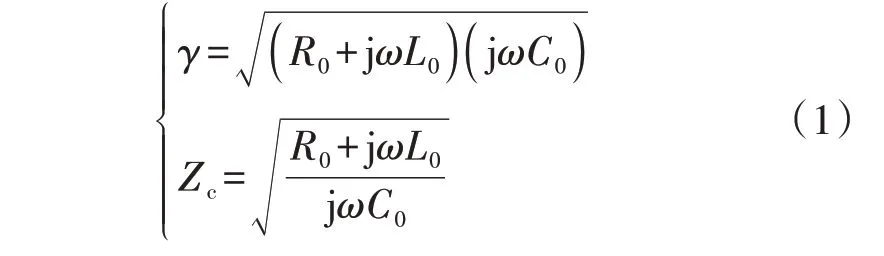
式中：ω为角频率。

长度为l的长距离输电线路的等值双端口π 型电路可以用以下计算公式表示：

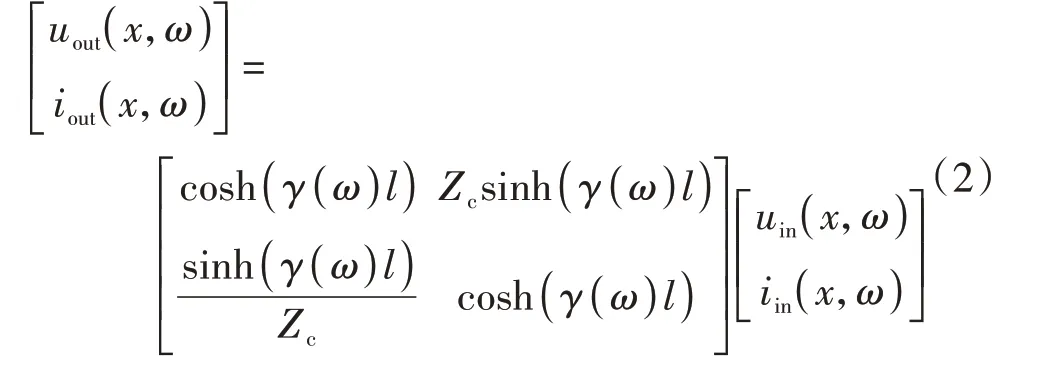
式中：uout(x，ω)、iout(x，ω)分别为双端口电路的输出电压和输出电流；uin(x，ω)、iin(x，ω)分别为双端口电路的输入电压和输入电流。

将式（2）按电压和电流重新分块整理，可以得到：

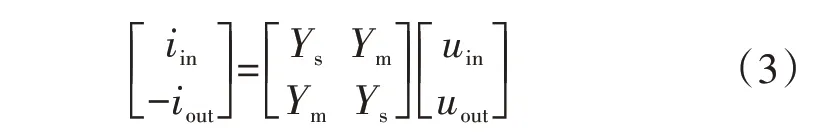
式中：Ys、Ym分别为该双端口电路中同一端口的自导纳和不同端口之间的互导纳，如式（4）所示。

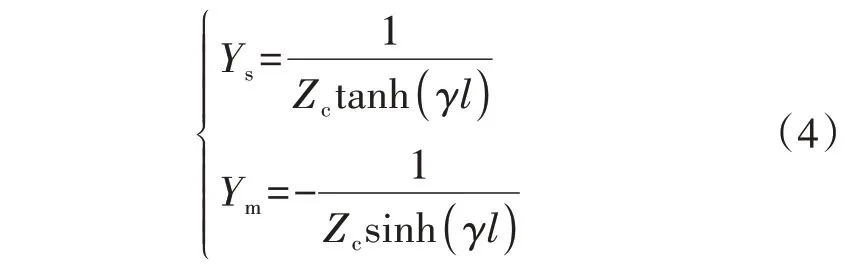
由此，根据式（3）与式（4）表示的电气关系，可以得到如图3 所示的牵引网双端口简化示意图。图中：R、L、C分别为线路距离为l的牵引网等值电阻、电感以及对地电容；Yopen、Yshort分别为图3（a）所示双端口等值电路某一端口下的开环导纳和短路导纳。

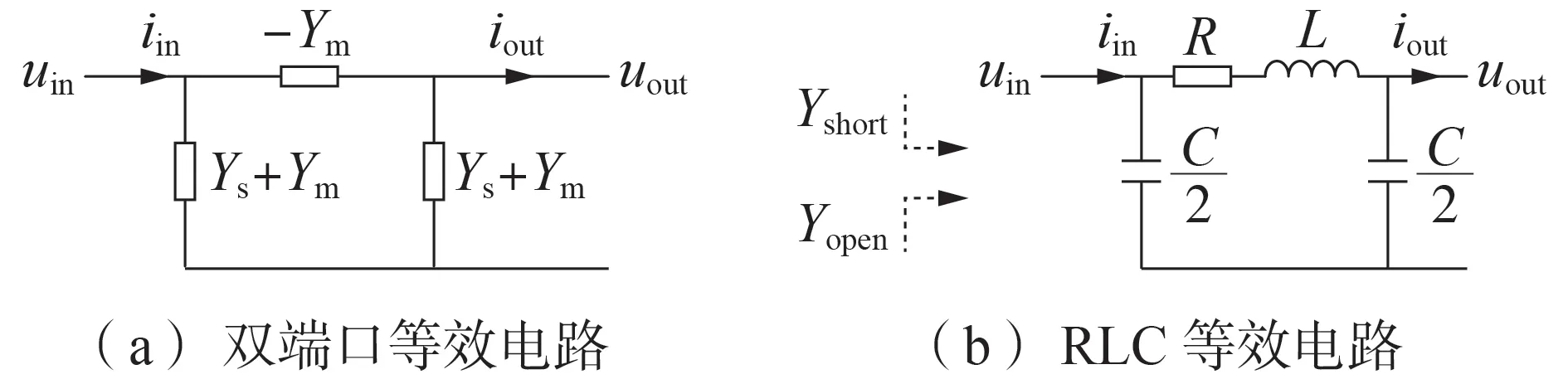
图3 牵引网双端口简化示意图Fig.3 Simplified diagram of dual-port traction network

根据图3（a），可得到Yopen和Yshort的理论计算表达式分别为：

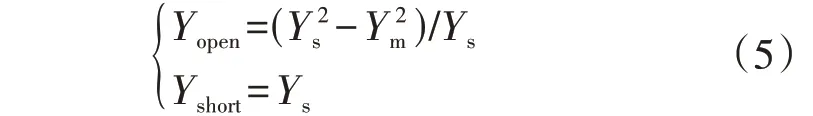
根据式（4）和式（5）可知，若能提前测量得到某一线路长度l下牵引网的开路导纳Yopen_m和短路导纳Yshort_m，则牵引网线路的传播系数和特征阻抗分别为：

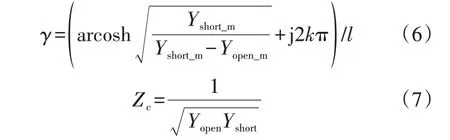
式中：k为整数。

由式（6）和式（7）可以得到牵引网线路的单位长度阻抗Z1(ω)和单位长度导纳Y1(ω)：

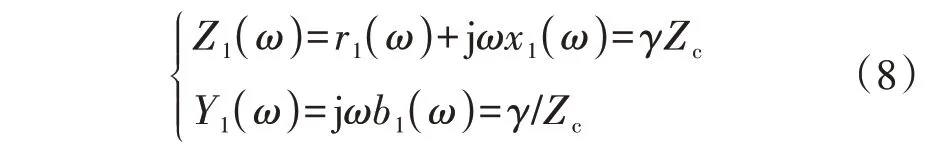
式中：r1(ω)为牵引网线路单位长度电阻；x1(ω)为牵引网线路单位长度电抗；b1(ω)为牵引网线路单位长度电纳。对照式（8）中系数可以得到：

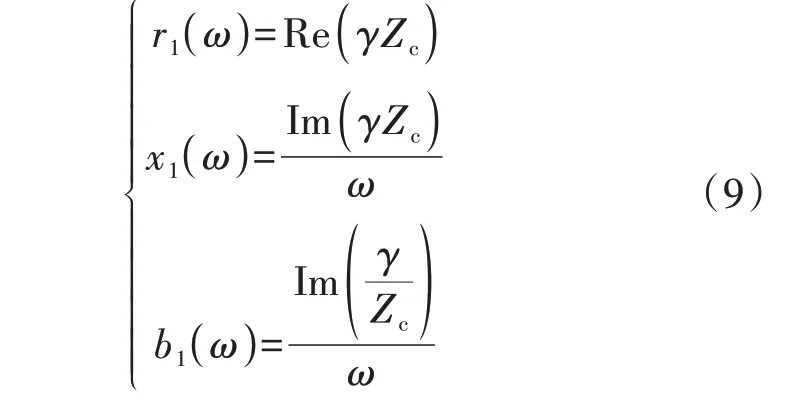
将按照式（6）与式（7）计算得到的传播系数γ和特征阻抗Zc代入式（4）得到同一端口自导纳和互导纳的计算值Ys_c、Ym_c，并代入式（5）得到开路导纳和短路导纳的计算值Yshort_c、Yopen_c，就可以得到任意线路长度为l的牵引网的双端口等效电路模型。

最后，将式（3）展开，可按端口电压写出方程：

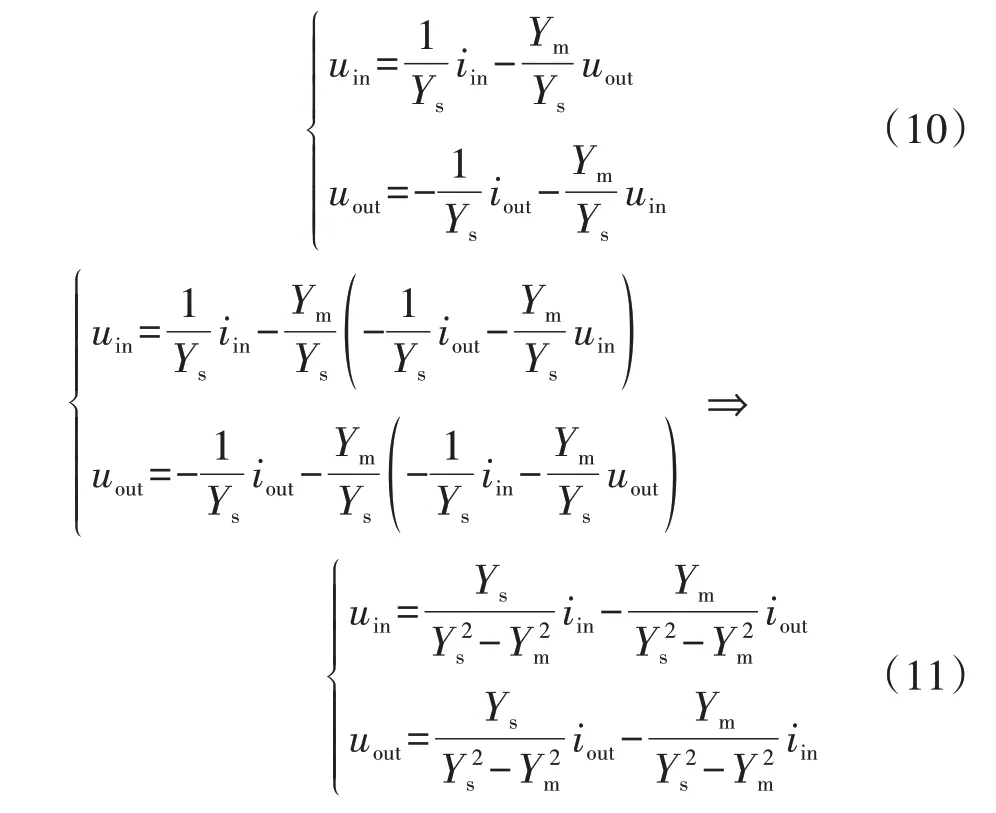
由式（10）与式（11）可见，输入、输出2 个端口各有4 个对应的等效电路，各等效电路中分别包含电压控制电压源（VCVS）、电压控制电流源（VCCS）、电流控制电压源（CCVS）以及电流控制电流源（CCCS），由此可见，理论上，牵引网的双端口电路模型应有16 个对应的等效电路模型。但值得一提的是，长距离传输线具有很强的对称特性，因此所建立的等效电路模型在2 个端口上的电参数是一致的。此外，当高速铁路列车（主要考虑列车变换器）和牵引网都在独立模式下工作时，牵引变电所输出电压uin和公共耦合点PCC（Point of Common Coupling）处电流iout是稳定的。因此，由式（10）与式（11）所得到的等效模型只有4个适用于本节的建模，如图4所示。

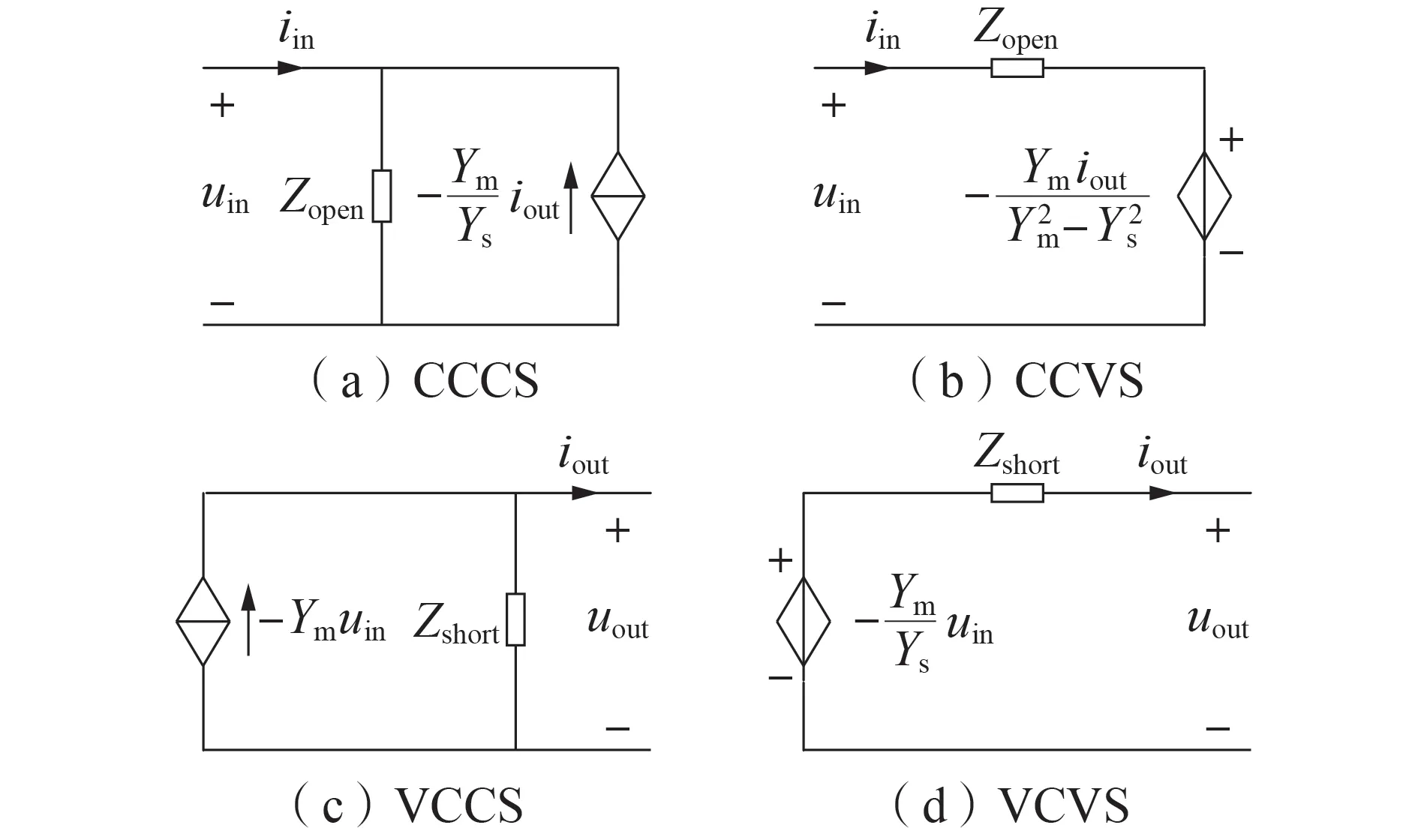
图4 牵引网双端口等效电路模型Fig.4 Dual-port equivalent circuit models of traction network

牵引网双端口等效电路模型建模流程如图5 所示。该等效模型中的牵引网分布参数γ和Zc是由实际测量的双端口电路的开路导纳Yopen_m和短路导纳Yshort_m计算得到的，由于牵引网参数沿线均匀分布，因此不同长度的相同类型的电力电缆具有相同的分布参数值，仅通过一次测量便可得到线路的分布参数，简化了传统牵引网需要多次测量参数的步骤。因此，通过该模型得到的传播系数和特征阻抗能够反映牵引网的分布特性。

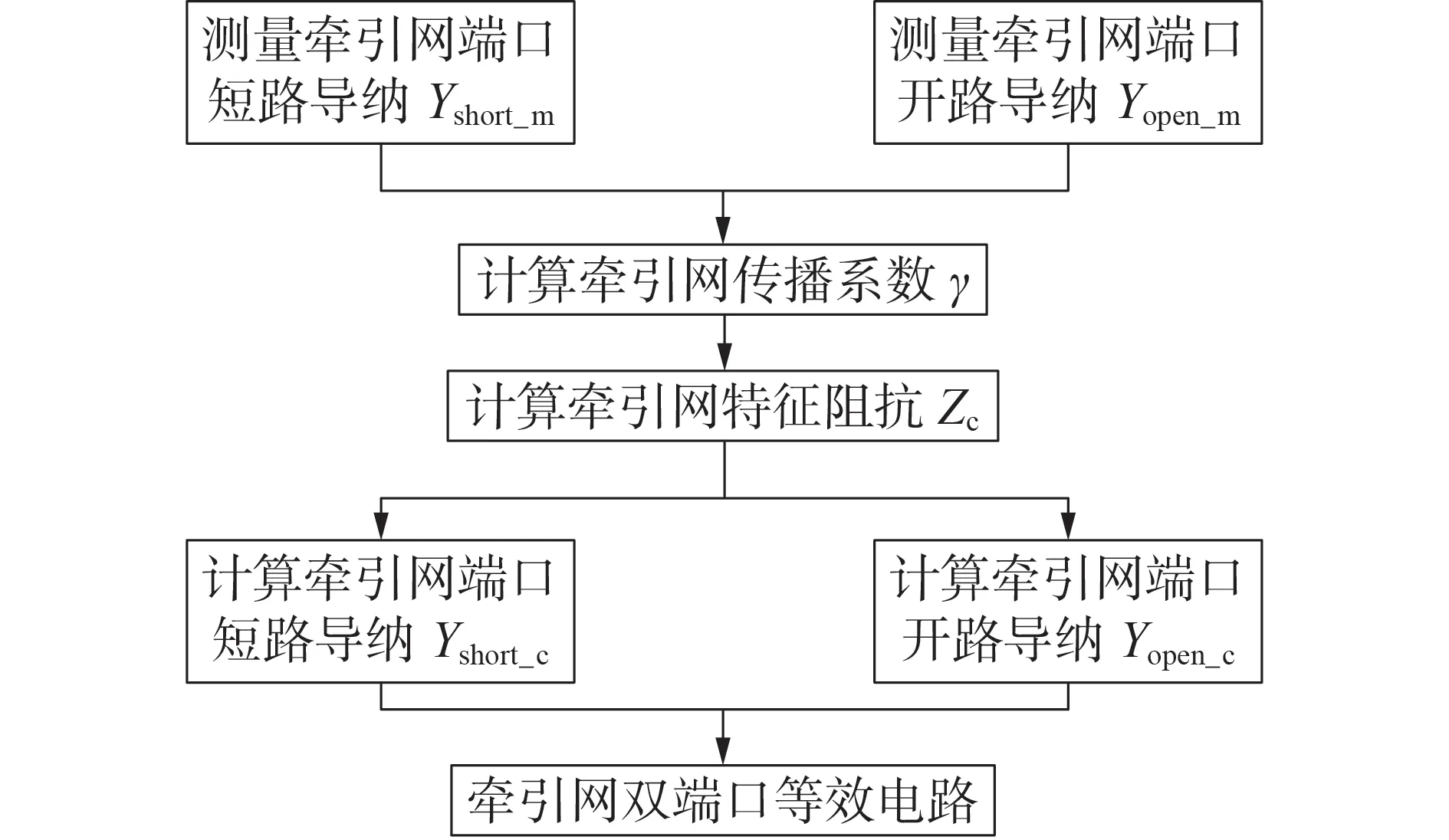
图5 牵引网双端口等效电路模型建模流程Fig.5 Flowchart of modeling process for dual-port equivalent circuit of traction network

2 牵引网双端口等效模型验证

2.1 理论论证

图3（b）所示简化电路的开路导纳和短路导纳分别为：

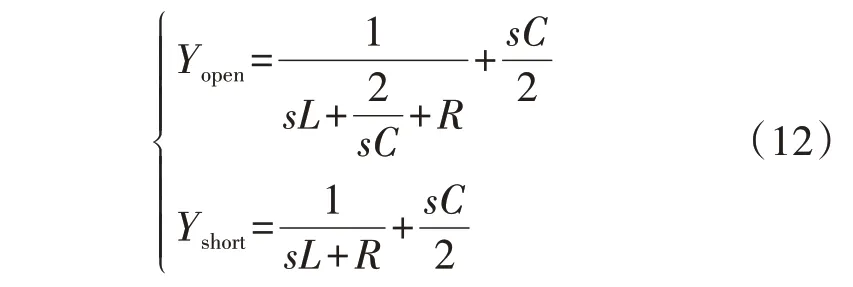
式中：R=r1l；L=x1l；C=b1l。根据式（6）可以得到该牵引网传播系数的计算值γcal为：

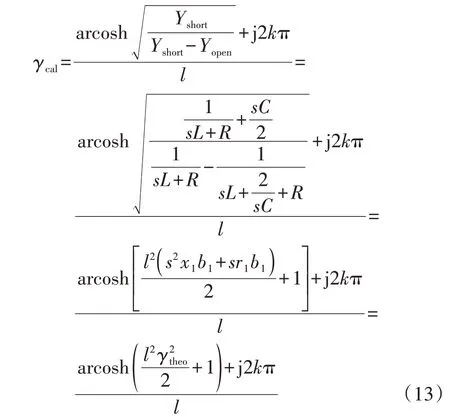
式中：γtheo=为理论传播系数。

同时，理论传播系数的双曲余弦函数的表达式为：

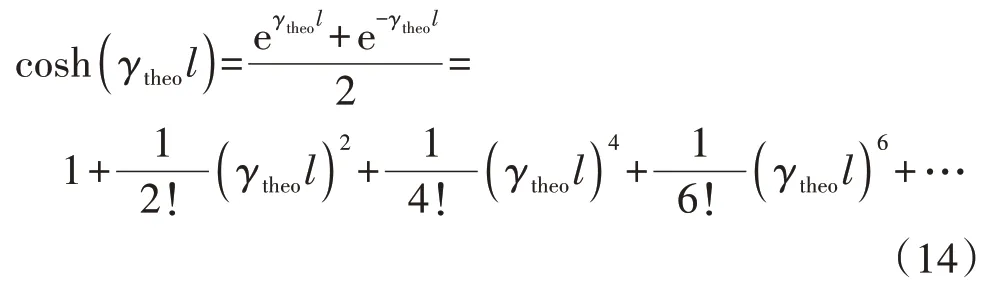
原则上，无限级联的π 型等效电路可以表征长距离传输线的端口阻抗特性，这意味着每个级联部分代表的输电线长度近似为0，因此，式（14）中的泰勒展开高阶项可以忽略不计，得到：

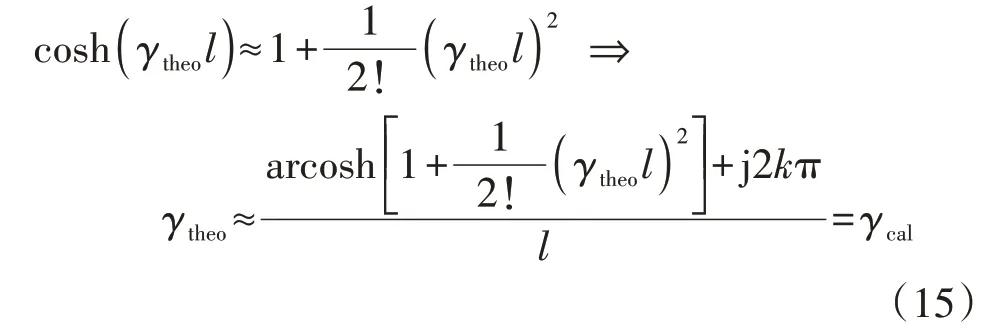
式（15）表明，本文所提方法可从测得的一端短路导纳和一端开路导纳中准确提取牵引网传播系数。

因此，本节所采用的牵引网双端口等效电路模型能够在考虑牵引网分布参数特性的同时简化为含受控源的戴维南-戴维南等效电路。

四川省广元市属集中连片贫困地区、革命老区、边远山区和地震重灾区“四区合一”的地区，农村贫困问题历来十分突出。2017年7月，广元市在四川省财政厅的大力支持下，率先在全省创新开展“政担银企户”财金互动扶贫试点工作，探索形成了以“政策引导为基础、农业担保为桥梁、金融投入为保障、主体带动为抓手、脱贫致富为目标”的财金互动广元扶贫模式，打通了财政金融扶贫“最后一公里”，有效解决了脱贫攻坚中农业产业发展融资难、融资贵问题和贫困户持续增收问题，切实起到为农、惠农、富农作用。

2.2 实际线路测量验证

基于渝利线丰都牵引变电所丰石供电臂实际线路的测量数据［13］，验证本文牵引网双端口等效电路建模方法在获取牵引网阻抗方面的准确性与可行性。渝利线实际线路横截面的各导体位置分布如附 录A 图A1 所 示［12］。接 触 线 与2 根 钢 轨 间 距 为6.45 m，线路供电臂长度为24.8 km［13］。附录A 图A2为渝利线丰都牵引变电所丰石供电臂末端短路分开供电试验电路示意图，基于附录A 图A2开展带回流线直接供电方式分开供电的短路实验（开关K1、201与291 断开，开关K2 与202 合闸，下行末端短路）。附录A表A1给出了该线路接触线数据。

附录A 图A3 为渝利线测试线路供电臂的开路导纳与短路导纳。图6 为采用等效双端口网络得到的开路导纳与短路导纳对比图。图7 为实际测得的接触线分布参数与利用双端口等效电路得到的牵引网分布参数对比图。

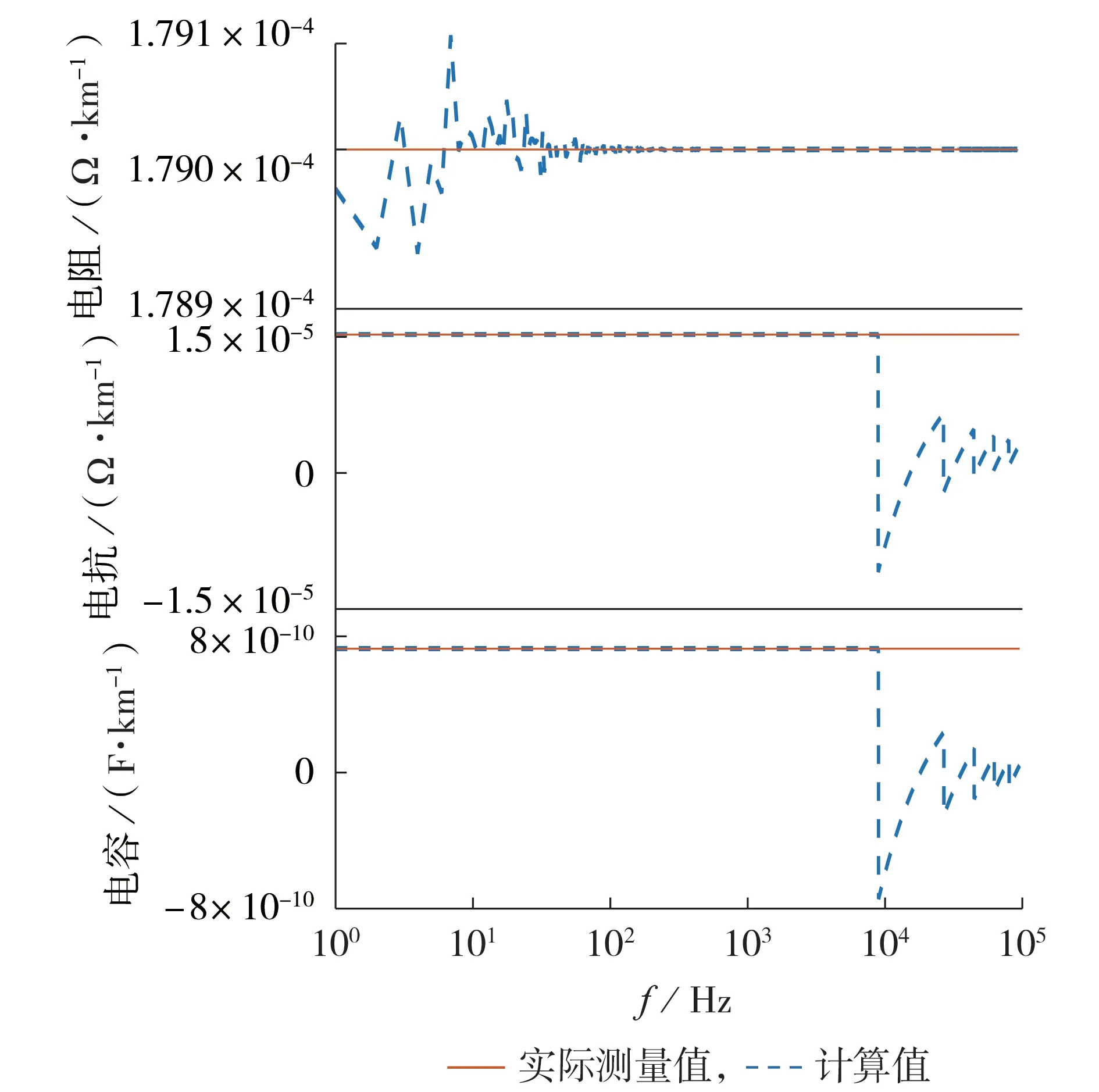
图7 分布参数对比Fig.7 Comparison of distribution parameters

由图6 可知，牵引网作为由RLC 元件组成的供电系统，其自身存在多个谐振点，当电力机车控制系统参数与机车运行状态存在谐振参数匹配时，电力机车受流处可能出现牵引网频率振荡的现象，危及牵引网供电系统安全。

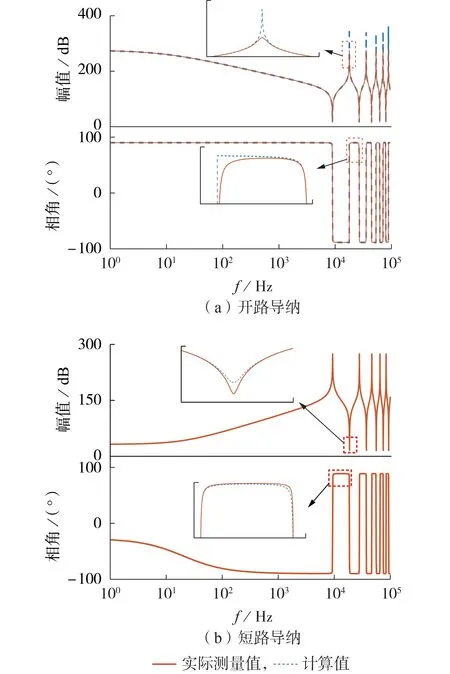
图6 采用等效模型所得导纳与实际测量导纳Fig.6 Admittance obtained by equivalent model and actual measurement

由图7 可知：在中低频范围内，利用所建牵引网模型得到的参数与实际测量参数吻合；在部分高频范围内，利用所建牵引网模型得到的参数与实际测量参数吻合，而在频率达到104Hz时，利用所建牵引网模型得到的电抗和电容参数与实际测量参数不吻合，并且出现骤减，这是由于本文模型只考虑了传播系数低阶泰勒展开项，当频率增大时，线路中需要计算的波长减小，式（14）中的高阶项无法忽略，如图6中放大部分所示，因此导致出现误差。总体而言，本文模型能够在反映牵引网分布参数特性的同时，保证牵引网模型的准确性。该模型极大降低了以往多导体传输线模型建模的复杂程度，为后续的阻抗分析奠定了基础。

3 基于阻抗的车网级联系统稳定性分析

3.1 牵引网模型线性化

由前述牵引网双端口等效电路建模方法可以得到牵引网双端口等效电路模型，如图8 所示。由于牵引网中只含有无源元件，且牵引网是线性网络，无耦合性，因此，对所建牵引网双端口等效模型进行线性化处理后模型仍保持原有的特性。根据图8 中的CCVS-VCVS 等效电路（戴维南-戴维南电路）列写出电压和电流方程：

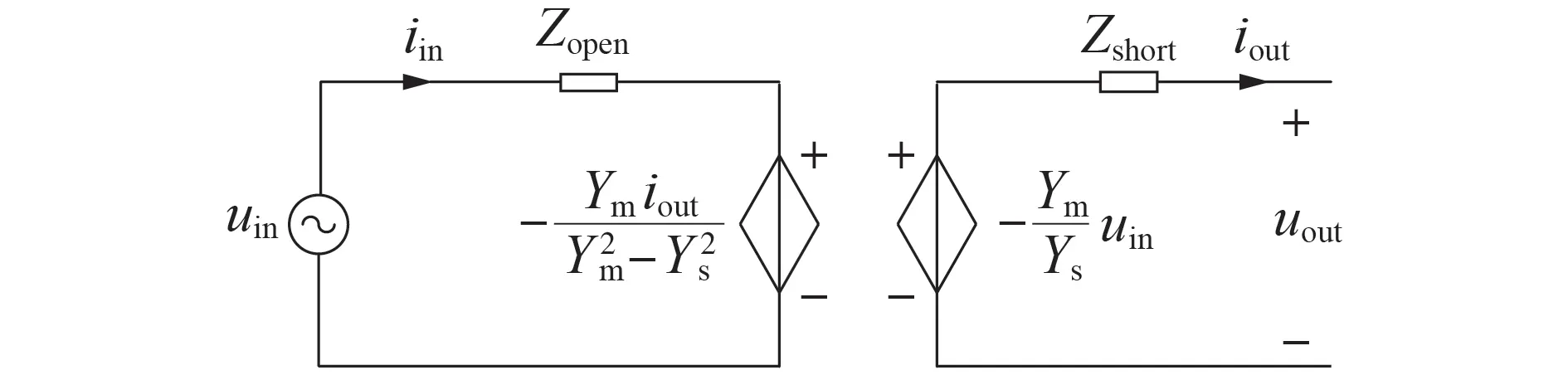
图8 牵引网CCVS-VCVS等效电路Fig.8 CCVS-VCVS equivalent circuit of traction network

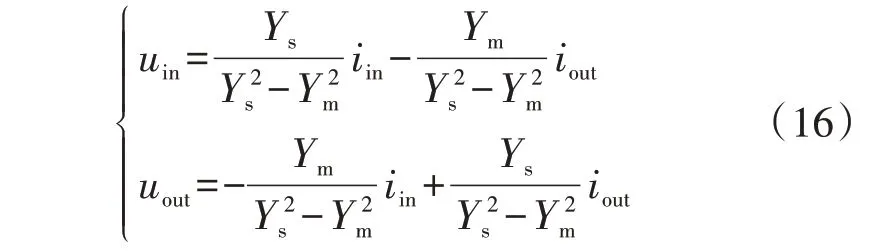
显然，由式（16）可以得到牵引网等效的输出阻抗Zs_eq为：

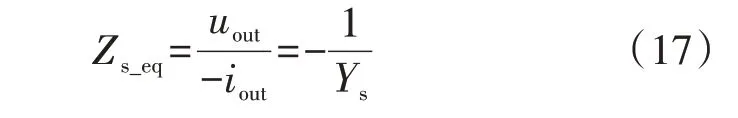
3.2 车网级联系统稳定性分析

本节将牵引网传统简单RL 等效模型与本文所提牵引网模型进行稳定性分析对比。RL等效模型接入时的波特图和系统波形分别见图9和图10，图中n为牵引供电臂数量，upcc为PCC 处电压，udc为直流侧电压。可知，当牵引网传统简单RL等效模型电阻为0.2 Ω、电感为2.9 mH，在进行阻抗理论值稳定性分析，图9 所示牵引网传统简单RL 等效模型波特图幅值和车侧整流器波特图幅值交点为51.65 Hz 时，对应的相角裕度为77.59-（-109.5）=187.09°>180°，此时应为不稳定的情况，而由图10 可知，在实际仿真分析时，系统为稳定情况，两者存在不匹配的情况，因此使用RL等效模型会存在稳定性误判的情况。

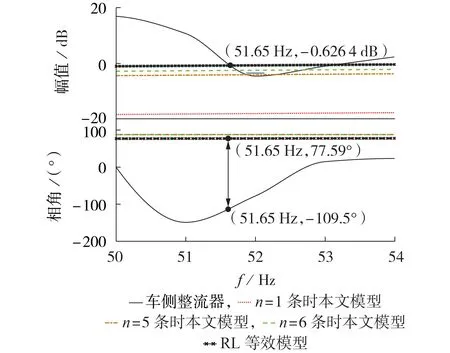
图9 RL等效模型接入时的波特图对比Fig.9 Comparison of Bode diagram when RL equivalent model is connected

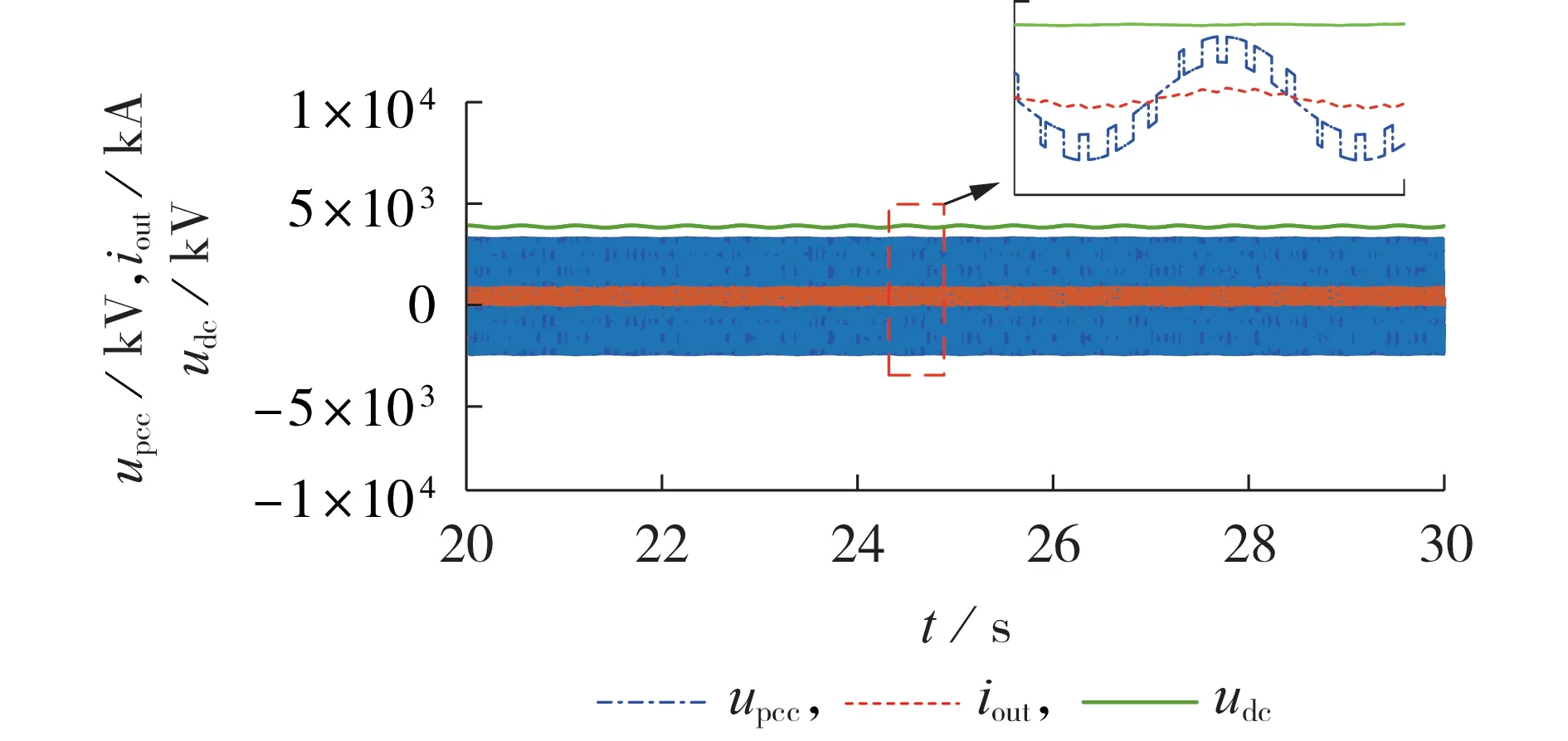
图10 RL等效模型接入时的系统波形Fig.10 System waveforms when RL equivalent model is connected

将本文所提牵引网双端口模型等效输入阻抗与CRH5 型车侧整流器［14］模型联结，构成车网级联系统，如附录A 图A4 所示。在MATLAB／Simulink 仿真平台上搭建仿真模型进行稳定性分析验证，各分布参数及车侧整流器控制参数如附录A表A2所示。

在不同牵引供电臂数量n下，分别进行PCC 处电压、电流和直流侧电压波形的仿真测试，结果见图11。由图可知，随着牵引供电臂数量的增加，PCC 处的电压、电流和直流侧电压均发生了明显的低频振荡，且振幅逐渐增大，在牵引供电臂数量n=6 条时，系统发生崩溃。可见，随着牵引网距离的增加，低频振荡发生的概率和剧烈程度会逐渐增加，为了有效避免车网耦合系统低频振荡的发生，应保持动车组与供电所的距离在1条供电臂的长度范围内。

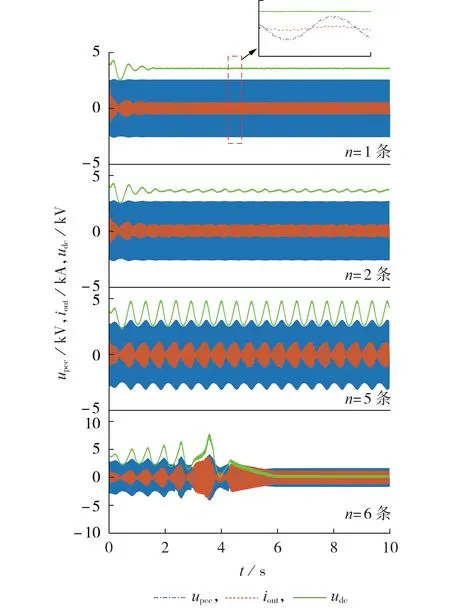
图11 PCC处电压、电流及直流侧电压波形图Fig.11 Voltage and current waveforms at PCC and voltage waveform at DC side

对于车网级联系统产生的低频振荡现象，采用波特图判据［15-16］进行稳定性分析。首先利用扫频法［17］获取1～1 000 Hz 频率范围内车侧整流器阻抗；然后针对不同的牵引网供电臂数量，将各阻抗与车侧整流器阻抗绘制在同一个波特图中，如附录A 图A5 所示。观察相角差为180°时系统的增益裕度可以发现，随着牵引网供电臂数量的增加，系统的增益裕度逐渐减小，这说明系统逐渐趋于不稳定，与仿真波形相吻合，同时也说明供电臂距离的增加会使系统的低频稳定性变差。

4 结论

针对牵引网系统，本文基于双端口网络理论，建立牵引网等效解耦电路模型，将其简化为含受控源的戴维南-戴维南等效电路，并通过实际牵引网线路测量数据，验证了该牵引网建模方法的可行性以及模型的准确性。采用本文牵引网建模方法所建模型具有以下2个优点。

1）该模型能够通过测得的一端短路导纳和一端开路导纳提取出牵引网的传播系数。在考虑牵引网分布参数特性的同时仅通过1 次测量便可得到线路的分布参数，简化了传统牵引网需要按照单位长度多次测量计算的步骤。

2）该模型降低了以往多导体传输线模型建模的计算复杂程度，解决了多导体链式模型难以直接用于系统稳定性分析的问题，为后续阻抗分析奠定了基础。

本文利用所建牵引网模型搭建车网级联系统，并对该系统进行稳定性分析研究，得到了随着牵引网距离的增加，低频振荡发生的概率和剧烈程度会逐渐增加的结论，为了有效避免车网耦合系统低频振荡的发生，应保持动车组与供电所的距离在较短的供电长度范围内。

附录见本刊网络版（http：//www.epae.cn）。