不平衡电压条件下双馈感应发电机混合直接功率控制策略

王一翔，孙士涛，程 鹏，马 静，贾利民，3

（1. 华北电力大学 国家能源交通融合发展研究院，北京 102206；2. 华北电力科学研究院有限责任公司，北京 100045；3. 北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044）

0 引言

近年来，基于双馈感应发电机（DFIG）的风电机组因具有变速运行、功率解耦控制、变频器额定容量较低等优点而得到了广泛的应用［1-2］，其主要控制策略包括矢量控制（VC）、直接功率控制（DPC）两大类。VC 通过电压矢量定向与旋转坐标系变换将三相电流解耦为有功电流、无功电流，分别构成有功电流、无功电流的闭环控制。DPC 可在无需电压矢量定向和旋转坐标变换的条件下，构造有功功率、无功功率的闭环控制，实现功率的无差跟踪控制。

然而，查表法DPC 策略使用了滞环控制器，会导致开关频率不固定、纹波大等现象发生。为了获取固定的开关频率，主要改进方法包括基于模型预测控制的直接功率控制（MPC-DPC）［3］和基于空间矢量调制的直接功率控制（SVM-DPC）［4-6］两大类：MPCDPC 通过构造目标函数以获取固定开关频率，但这种非线性控制的实施较复杂，计算负担大；SVM-DPC通过空间矢量调制进行调制电压合成，可在采用常规线性控制器的条件下获取固定的开关频率，具有控制结构简单、易于实现等优点。

近年来，文献［7-12］在SVM-DPC 结构框架下对不平衡电压条件下DFIG 的控制进行了研究。文献［7-8］通过在有功功率、无功功率参考值中加入相应的功率补偿项，实现了并网功率、负序电流的灵活控制；文献［9］构造了2 倍频功率控制器，以获取相应的负序励磁电压。上述控制策略需根据正、负序电压和电流分量计算2 倍频功率分量，从而获取适用于不平衡电压条件下2 倍频功率控制的励磁电压。文献［10-12］引入拓展无功功率理论，通过组合常规功率与拓展功率，可在无需对并网电流进行正、负序分离的情况下消除有功功率或无功功率的2 倍频波动分量。然而，上述控制策略着眼于构建适用于不平衡电压条件下有功功率、无功功率的目标指令，很少关注多运行目标下功率反馈值的灵活配置。

为此，本文结合常规功率与拓展功率，提出了混合直接功率控制（H-DPC）策略：首先，构造了有功功率、无功功率的调制电压，可在无需锁相同步的条件下实现对DFIG定子有功功率、无功功率的无差跟踪控制；然后，通过常规功率与拓展功率的灵活组合，在无需电压、电流相序分离的条件下，设计了可消除DFIG 定子有功功率／无功功率的2 倍频波动分量及定子负序电流的功率反馈量；最后，基于RTLAB硬件在环实验验证了所提H-DPC策略的有效性。

1 数学模型

1.1 功率分析

在本文的研究中，假设三相三线电网含有负序电压，且没有零序电压和谐波畸变，则在αβ两相静止坐标系下的电压、电流可分别表示为：

式中：usα、usβ和isα、isβ分别为DFIG定子电压和电流的α、β轴分量；下标“+”、“-”分别表示正序、负序分量；Us+、Us-和Is+、Is-分别为正、负序电压和电流的幅值；θu+、θu-和θi+、θi-分别为正、负序电压和电流的初始相位；ωg为电网角频率。

根据常规功率理论，DFIG 定子的视在功率可表示为：

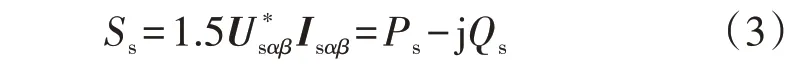
式中：Ss、Ps、Qs分别为DFIG 定子的常规视在功率、有功功率、无功功率；Usαβ=usα+jusβ、Isαβ=isα+jisβ分别为定子电压、电流矢量；上标“∗”表示共轭。

在不平衡电压条件下，DFIG 定子的常规有功功率、无功功率均包含平均分量和2 倍频波动分量，即：

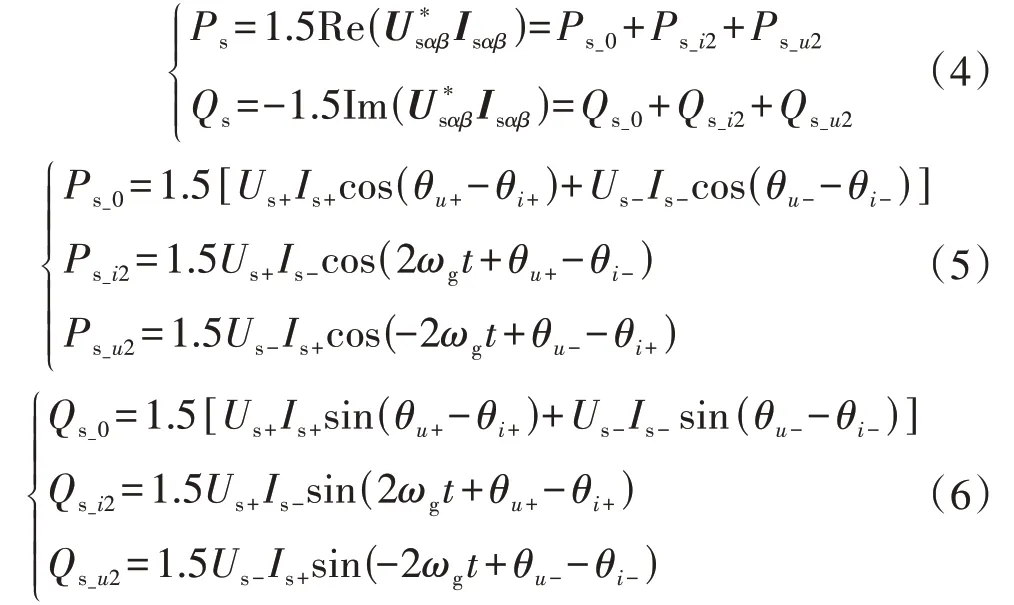
式中：Re、Im 分别表示实部、虚部；Ps-0、Qs-0分别为常规有功功率、无功功率的平均分量；Ps-i2、Qs-i2分别为由正序电压和负序电流引起的常规有功功率、无功功率的2 倍频波动分量；Ps-u2、Qs-u2分别为由负序电压和正序电流引起的常规有功功率、无功功率的2倍频波动分量。

拓展功率理论采用1/4周期延时（滞后90°）的电压与实时测量电流作为变量，其中1/4周期延时的电压可表示为：

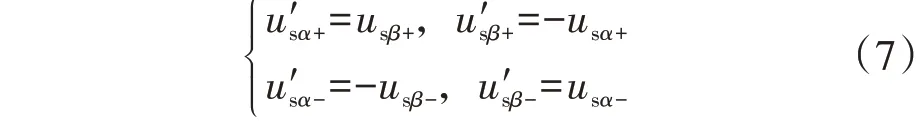
式中：上标“′”表示1/4周期延时。

则DFIG 定子的拓展有功功率Ps_ex和拓展无功功率Qs_ex可表示为：

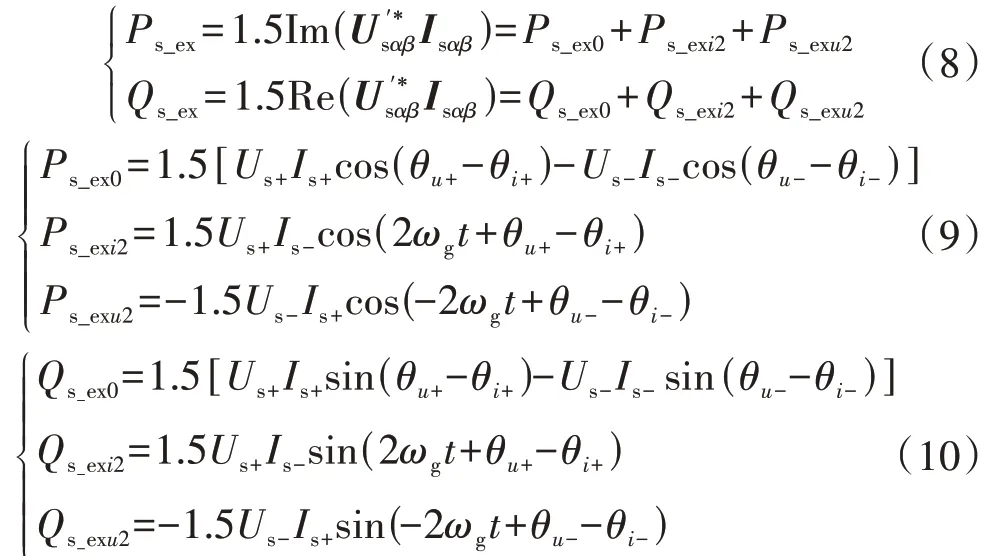
式中：Ps_exi2、Qs_exi2分别为由正序电压和负序电流引起的拓展有功功率、无功功率的2 倍频波动分量；Ps_exu2、Qs_exu2分别为由负序电压和正序电流引起的拓展有功功率、无功功率的2 倍频波动分量；为1/4周期延时后的定子电压共轭矢量。

通过对比式（5）、（6）、（9）、（10），可得：

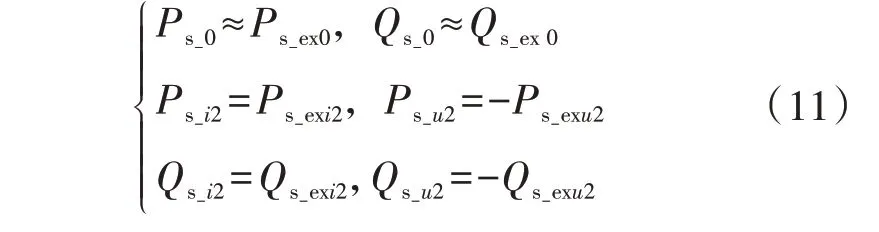
可见，由正序电压和负序电流引起的常规与拓展有功功率／无功功率的2 倍频波动分量相等，而由负序电压和正序电流引起的常规与拓展有功功率／无功功率的2 倍频波动分量互为相反数。需要指出的是，由负序电压和电流产生的平均有功功率和无功功率相对较小，可将其近似视为0，因此，在不平衡电压条件下，常规有功功率／无功功率与拓展有功功率／无功功率的平均分量相等。

1.2 DFIG模型

两相静止坐标系下DFIG 的等效电路如图1 所示，则DFIG电压和磁链的动态方程分别为：

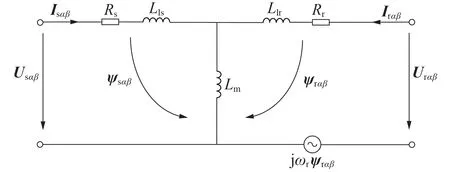
图1 静止参考系下DFIG的等效电路Fig.1 Equivalent circuit of DFIG in stationary reference frame

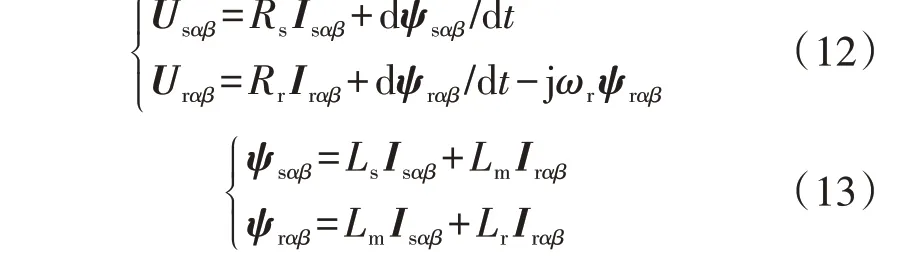
式中：ψsαβ、ψrαβ分别为定、转子磁链矢量；Urαβ、Irαβ分别为转子电压、电流矢量；Rs、Rr分别为定子、转子电阻；ωr为转子角频率；Lm为互感；Ls=Lm+Lls、Lr=Lm+Llr分别为定子、转子自感，Lls、Llr分别为定子、转子的漏电感。

根据式（13），DFIG 的转子磁链、转子电流可分别表示为：

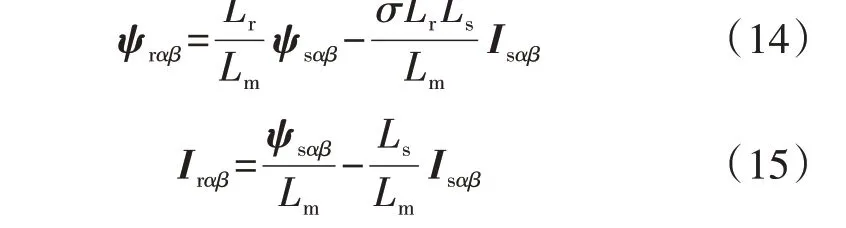
式中：σ=1-/(LsLr)为漏磁系数。

将式（14）和式（15）代入式（12）的转子电压动态方程中，可得DFIG定子电流的动态方程为：

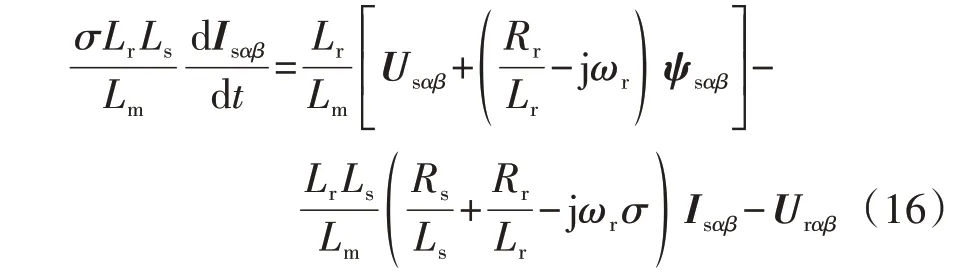
由于转子电阻Rr远小于转子自感Lr，定子电阻Rs远小于定子自感Ls，为了简化模型，可以认为式（16）中的Rr/Lr、Rs/Ls为0，则定子电流的动态方程可简化为：

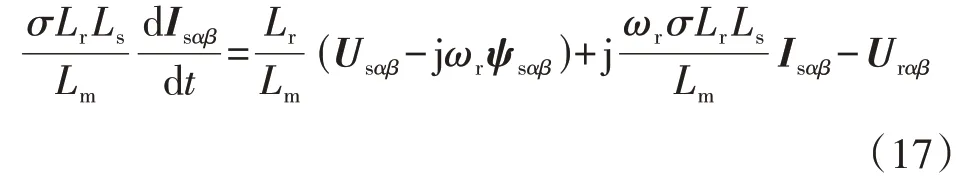
根据式（1）和式（7），DFIG 定子电压的动态方程可表示为：

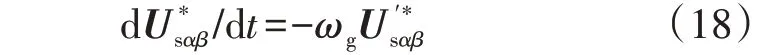
则DFIG视在功率的动态方程可表示为：

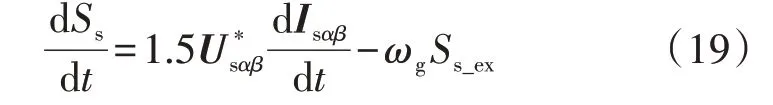
式 中：Ss_ex=1.5Isαβ=Qs_ex+jPs_ex为DFIG 定 子 的 拓展视在功率。

将式（17）代入式（19），可得：

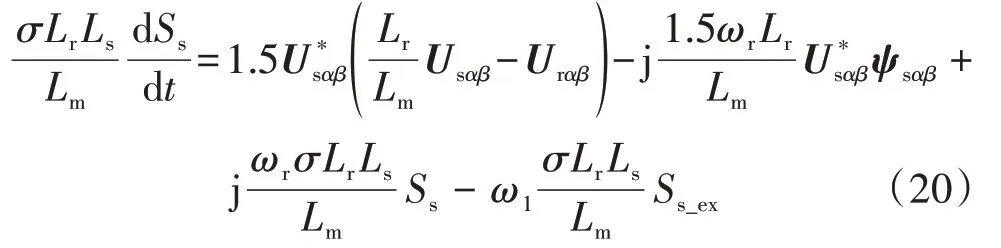
式中：ω1为电网的标称角频率。

考虑到电网的实际频率偏差相对较小［13-14］，为了简化控制模型，在基频频率为50 Hz 的电网环境下，可采用标称角频率ω1=100π rad／s 代替式（19）中的实际角频率ωg。因此，式（20）可改写为：

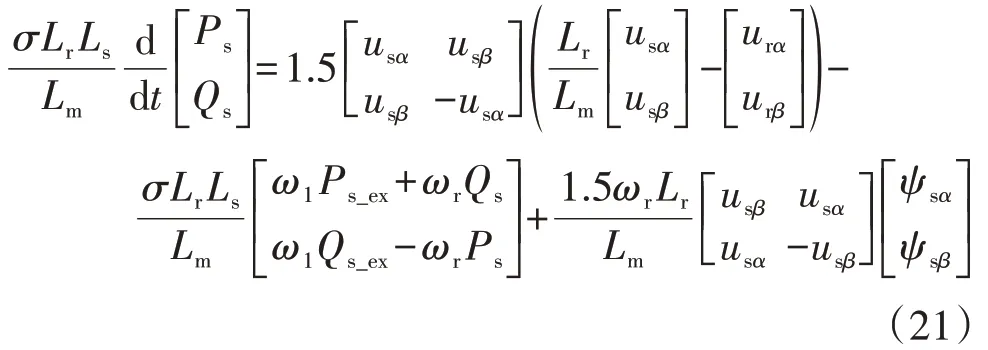
可以注意到，在式（21）中DFIG 有功功率和无功功率的动态方程含有与交流电压相关的系数，这使其成为时变系统。为了将时变系统变为时不变系统，将有功功率的调制电压uP和无功功率的调制电压uQ定义为：

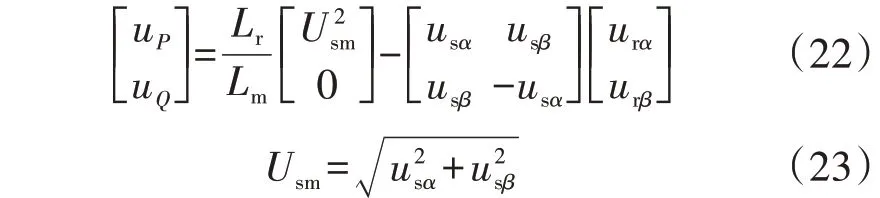
式中：Usm为定子电压的幅值。

由于引入了有功功率和无功功率的调制电压，则DFIG有功功率和无功功率的动态方程可简化为：

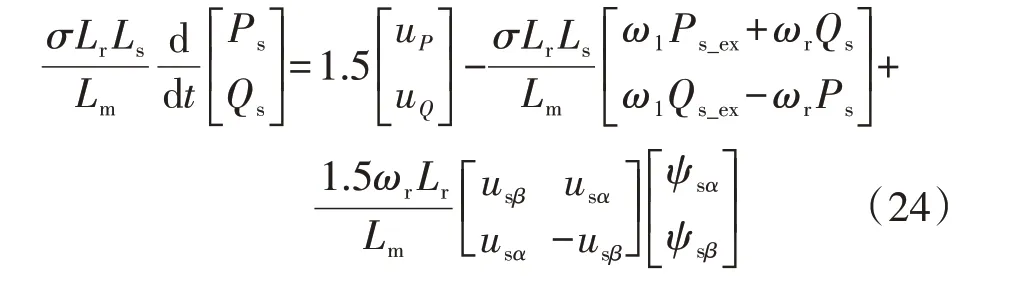
由式（24）可见，由于引入了DFIG 有功功率和无功功率的调制电压，DFIG 有功功率和无功功率的时变微分方程被转化为时不变常系数方程，为采用比例-积分等线性控制器提供了理论基础。

2 控制系统

2.1 控制系统设计

不平衡电压会导致DFIG 定子出现不平衡电流、2 倍频波动功率等负面效应，继而进一步恶化DFIG的运行性能。为了增强DFIG 对不平衡电网环境的适应性，可设置如下3 个控制目标：①目标1，消除DFIG 定子有功功率的2 倍频波动分量；②目标2，消除DFIG 定子无功功率的2倍频波动分量；③目标3，消除DFIG定子的负序电流。

1）针对目标1，由于DFIG 定子有功功率的2 倍频波动分量为0，根据式（5），有Ps-i2+Ps-u2=0，则DFIG定子负序电流的幅值与相位可表示为：

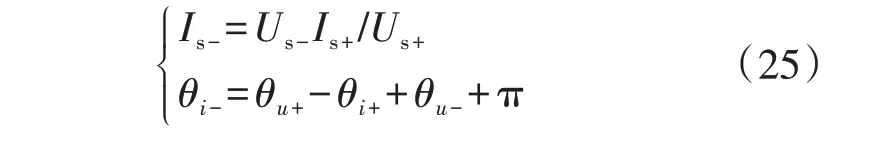
则DFIG 定子拓展无功功率的2 倍频波动分量可表示为：

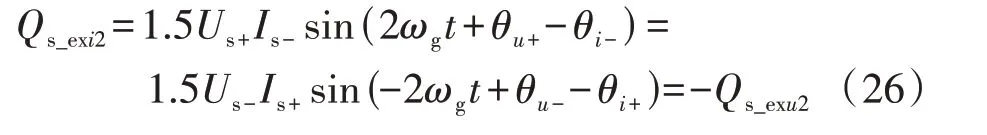
可见，DFIG 定子拓展无功功率的2 倍频波动分量互为相反数，则DFIG定子的拓展无功功率为恒定直流量形式。换言之，当设置目标1 时，DFIG 定子常规有功功率和拓展无功功率的2 倍频波动分量可同时被消除。因此，DFIG 功率控制闭环的反馈量可设置为：

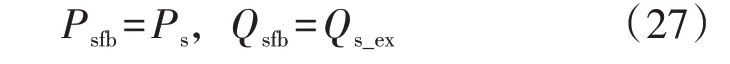
式中：Psfb、Qsfb分别为DFIG 定子有功功率、无功功率的闭环反馈量。

2）针对目标2，由于DFIG 定子无功功率的2 倍频波动分量为0，根据式（6），有Qs-i2+Qs-u2=0，则DFIG定子负序电流的幅值与相位可表示为：

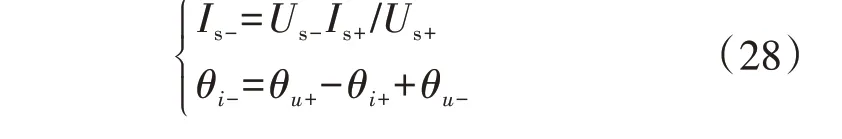
DFIG 定子拓展有功功率的2 倍频波动分量可表示为：

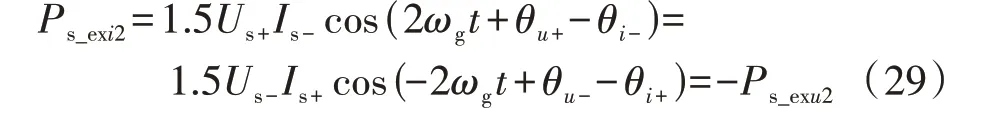
可见，DFIG 定子拓展有功功率的2 倍频波动分量互为相反数，则DFIG定子的拓展有功功率为恒定直流量形式。换言之，当设置目标2 时，DFIG 定子常规无功功率和拓展有功功率的2 倍频波动分量可同时被消除。因此，DFIG 功率控制闭环的反馈量可设置为：

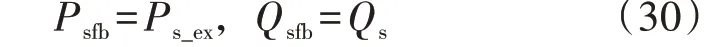
可以注意到，基于式（12），DFIG 定子拓展功率和常规功率的平均值相等，若按照式（28）正确输入负序电流，则DFIG定子拓展有功功率和常规无功功率的2倍频波动分量为恒定值。

3）针对目标3，由于DFIG 定子的负序电流为0，由负序电流和正序电压引起的常规有功功率和无功功率的2 倍频波动分量为0，即Ps-i2=Qs-i2=0。但是，由负序电压和正序电流引起的常规有功功率和无功功率的2 倍频波动分量仍然存在，即Ps-u2≠0，Qs-u2≠0。

由于DFIG 定子常规和拓展有功功率／无功功率的2 倍频波动分量总是相反且与负序电流无关，通过将常规和拓展功率相加，可获得恒定的功率反馈。由于相加后总的平均分量是恒定功率参考值的2 倍，为了保证平均功率输出，需乘以取值为0.5 的附加系数，则DFIG 功率控制闭环的反馈量可设置为：

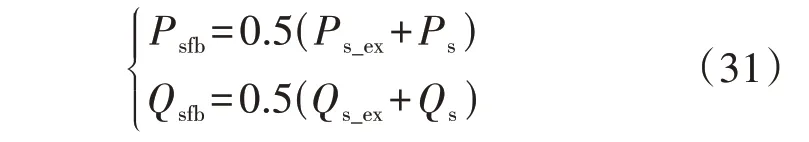
根据上述分析可知，在不平衡电压条件下，实现消除有功功率和无功功率的2 倍频波动分量以及定子负序电流这3 个控制目标所需注入的负序电流各不相同，则无法控制DFIG 同时实现上述3 个控制目标。

2.2 控制系统实施

在不平衡电压条件下，为了实施对DFIG 定子功率平均直流量与2 倍频交流量的无差跟踪控制，可采用比例-积分-谐振PI+R（Proportional Integral plus Resonant）调节器。由于实际电网频率与额定电网频率之间存在微小偏差，为了降低实际电网频率与额定电网频率之间的偏差对PI+R 调节器的影响，通常引入截止角频率ωc，则PI+R 调节器的传递函数G(s)可表示为：

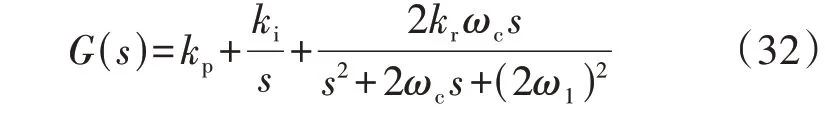
式中：kp、ki、kr分别为比例、积分、谐振系数；后续研究中设置截止角频率ωc的取值为10 rad／s。

根据式（24），可计算得到DFIG 定子有功功率、无功功率的调制电压为：

式中：vP、vQ分别为有功、无功功率控制器的输出；Psref、Qsref分别为DFIG 定子有功功率、无功功率的目标参考值。

根据式（22），在两相静止坐标系下，DFIG 转子励磁电压与有功功率、无功功率调制电压之间的关系可表示为：

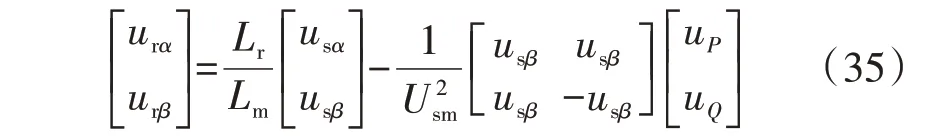
然后，结合转子的位置角，获取在转子两相静止坐标系（相对定子两相静止坐标系以转子角频率旋转）下DFIG转子励磁电压，如式（36）所示。

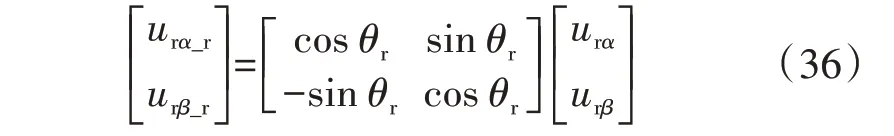
式中：urα_r、urβ_r为DFIG 转子两相静止坐标系下的转子电压；θr为转子的位置角。

H-DPC 结构框图如图2 所示。图中：usabc和isabc分别为三相定子电压和电流；Vdc为直流侧电压。可见，H-DPC 结构主要包括3 个环节：①功率反馈生成环节，可结合设置的控制目标，根据式（27）、（30）、（31），生成相应的功率反馈量；②功率跟踪环节，采用PI+R 调节器实现呈现平均直流量与2 倍频交流量形式的混合功率对目标功率的无差跟踪控制；③励磁电压生成环节，根据式（35）和式（36）实现有功功率、无功功率调制电压与DFIG转子励磁电压之间的转换。可见，采用本文所提H-DPC 策略，在两相静止坐标系下构建有功功率、无功功率调制电压而无需锁相电压矢量定向，同时可在无需对电压、电流进行相序分离与提取的情况下，实现对DFIG定子功率的2 倍频分量与负序电流的控制，增强DFIG 应对不平衡电压的运行控制能力。

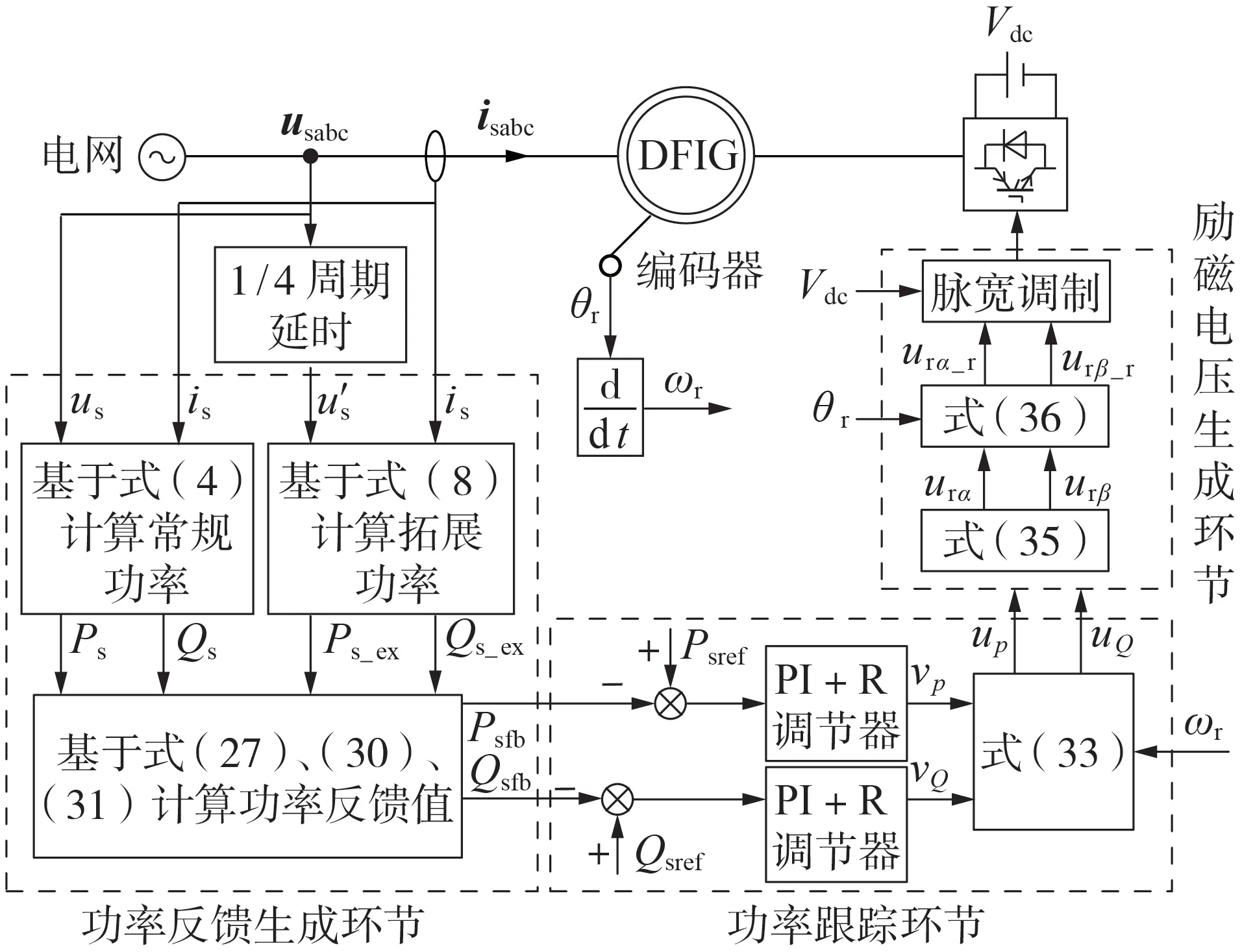
图2 H-DPC结构框图Fig.2 Structure diagram of H-DPC

3 硬件在环实验

为了验证本文所提H-DPC 策略的有效性，在RTLABOP5700 与NIPXIe 1071 构成的硬件在环实验平台上进行实验研究，硬件在环实验平台和DFIG相关参数分别见附录A图A1和表A1。

在硬件在环实验中，主电路运行在RTLAB 中，通过模拟输出H-DPC 实施所需的电压、电流信息；H-DPC 策略运行在NI PXIe 1071 中，输出控制变流器的脉冲信号，并设置以下4种运行模式。

1）模式1：采用式（4）给出的常规有功功率、无功功率作为功率反馈量。

2）模式2：以消除DFIG 定子有功功率的2 倍频波动分量为目标，采用式（27）所示混合功率作为功率反馈量。

3）模式3：以消除DFIG 定子无功功率的2 倍频波动分量为目标，采用式（30）所示混合功率作为功率反馈量。

4）模式4：以消除DFIG 定子的负序电流为目标，采用式（31）所示混合功率作为功率反馈量。

平衡电压条件下DFIG 功率阶跃实验结果如图3 所示。由于电机的机械时间常数与电磁时间常数存在数量级差别，可假设DFIG 的转子速度为1.2 p.u.（超同步）。在硬件在环实验中，DFIG采用运行模式2，即以常规有功功率、拓展无功功率作为功率反馈量，其有功功率目标参考值设定为1.0 MW，在200 ms时阶跃为1.6 MW，在450 ms时恢复为1.0 MW，而其无功功率目标参考值设定为0，在300 ms 时阶跃为0.4 Mvar（容性），在400 ms 时恢复为0。可见，DFIG 的有功功率和无功功率可以快速、无差地跟踪其目标参考值，且其定子电流和转子电流保持高正弦度，总谐波畸变率（THD）分别为2.3%和2.2%。

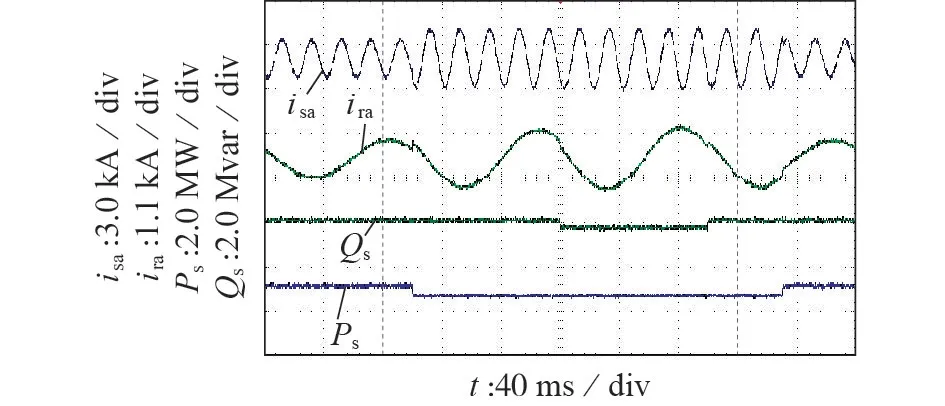
图3 平衡电压条件下DFIG功率阶跃实验结果Fig.3 Experimental results of DFIG power step under balanced voltage condition

不平衡电压条件下DFIG 多目标控制的实验结果如图4 所示（图中Te为电磁转矩）。其中，DFIG定子有功功率、无功功率的目标参考值分别设置为2.0 MW、0。在［0，100］ms内，采用运行模式1，DFIG定子有功功率、无功功率的2 倍频波动分量得到抑制，但DFIG 定子电流存在明显的谐波畸变，THD为10.2%，其中以3次谐波含量最高，达到9.9%。在100 ms 后，采用H-DPC 策略，DFIG 定子电流谐波得到明显抑制，THD下降为1.8%。在（100，200］ms内，采用运行模式2，可消除DFIG 定子有功功率的2 倍频波动分量，而DFIG 定子无功功率的波动幅度达到19.8%，同时引入表征负序电流幅值与正序电流幅值比值的电流不平衡度CUF（Current Unbalance Factor），其值约为10.8%。在（200，300］ms 内，采用运行模式3，DFIG 定子无功功率的2 倍频波动分量得到明显抑制，但其定子有功功率的波动幅度升高到19.2%，定子三相CUF为9.1%。在（300，400］ms内，采用运行模式4，DFIG 定子电流三相平衡，其CUF 下降为0.1%，此时DFIG 有功、无功功率的波动幅度分别为9.3%、9.6%。可见，采用H-DPC 策略可在保证DFIG 定子电流高正弦度的基础上，实现对DFIG 定子有功功率、无功功率2 倍频波动分量以及定子负序电流的有效抑制，增强DFIG在不平衡电压条件下的运行能力。

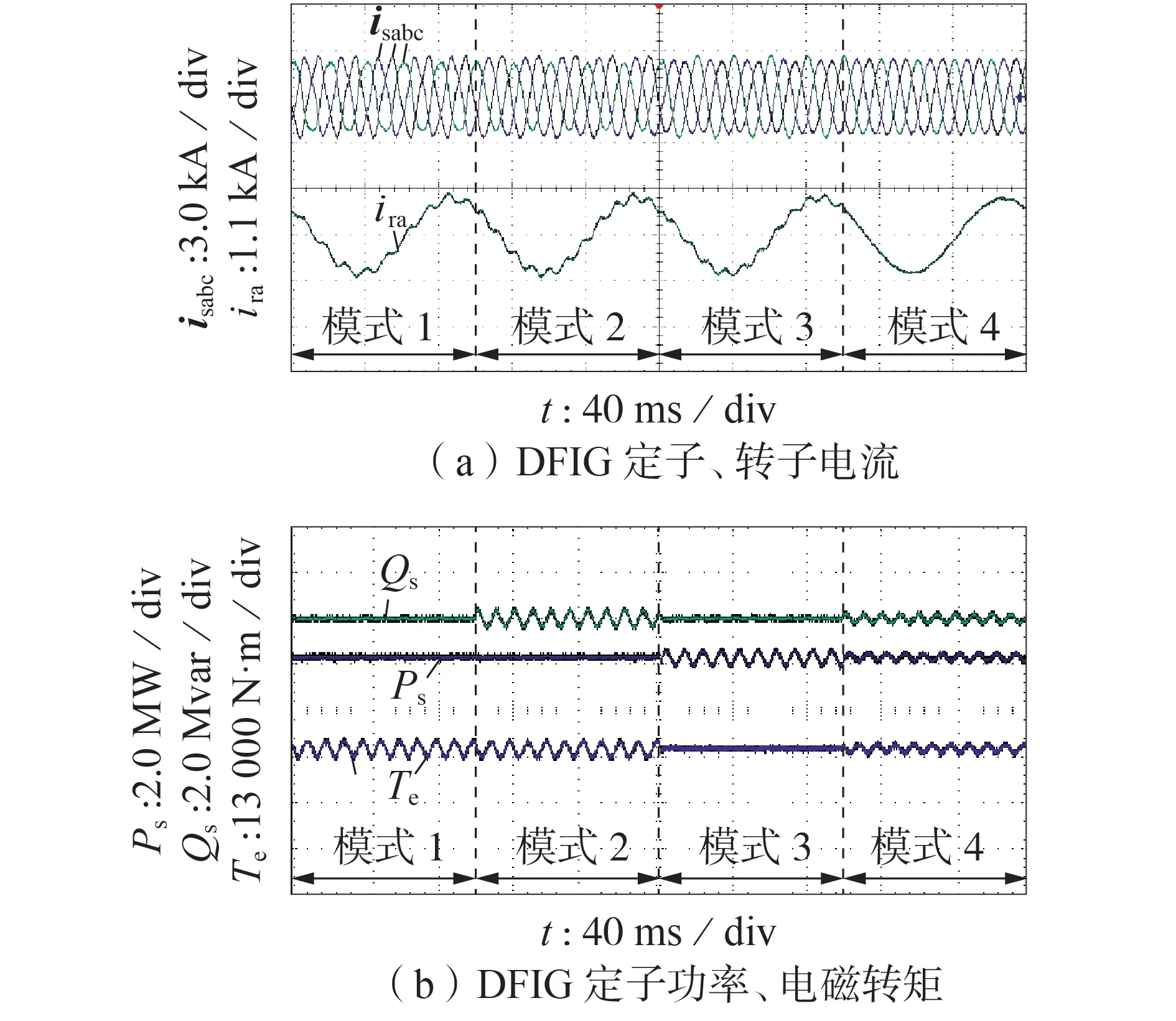
图4 不平衡电压条件下DFIG多目标控制的实验结果Fig.4 Experimental results of multi-objective control for DFIG under unbalanced voltage condition

为了对比不同的运行模式下DFIG 的并网特性，表1 给出了DFIG 定子电流THD、CUF 以及定子有功功率、无功功率2 倍频分量的波动幅度。由表可知，相较于运行模式1，H-DPC 可显著降低DFIG 定子电流的THD，保证高正弦度DFIG 定子电流输出，实现对有功和无功功率2 倍频波动分量及DFIG 定子负序电流的有效抑制，有效降低DFIG 电磁转矩的2 倍频波动分量，削弱不平衡电压对DFIG运行特性的负面影响，增强不平衡电压下DFIG的运行控制能力。

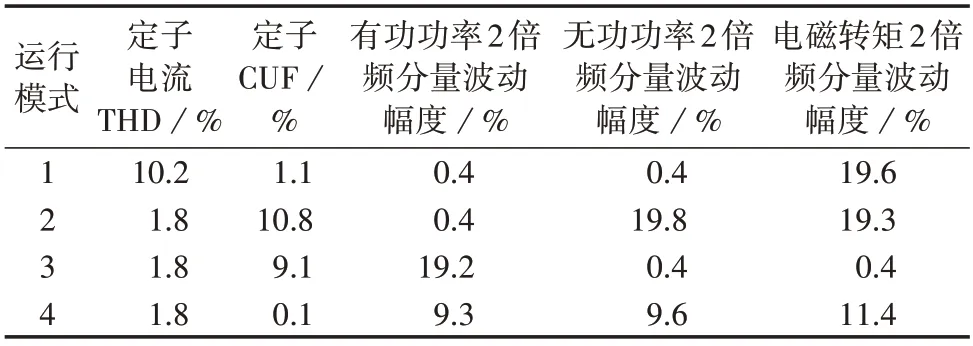
表1 不平衡电压条件下DFIG的运行性能比较Table 1 Comparison of DFIG’s operation performance under unbalanced voltage condition

为了进一步验证采用H-PDC 策略的DFIG 在瞬态不平衡电压扰动下的动态性能，图5 给出了在10%瞬时不平衡电压下DFIG暂态响应的实验结果，其中在200 ms 时出现10%瞬态不平衡电压。在实验中，DFIG 的有功功率、无功功率的目标参考值分别设置为2.0 MW、0，且采用运行模式2，即以消除DFIG 定子有功功率的2 倍频波动分量为目标。为了消除DFIG 定子有功功率的2 倍频波动分量，需注入式（28）所示的DFIG 定子负序电流，这不可避免地导致DFIG 转子电流存在110 Hz 谐波分量。在瞬态负序电压扰动发生后，H-DPC 可快速消除定子有功功率的2 倍频波动分量，并实现反馈功率的无差跟踪控制，且DFIG的暂态响应时间约为15 ms。

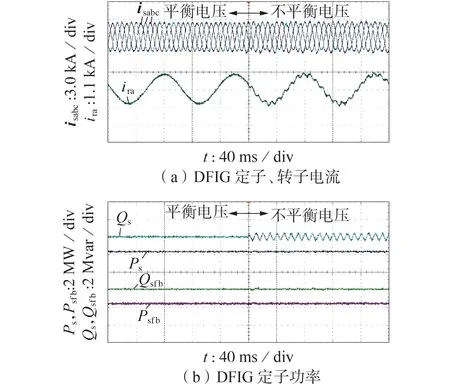
图5 不平衡电压条件下DFIG暂态响应的实验结果（模式2）Fig.5 Experimental results of DFIG’s transient response under unbalanced voltage condition（Mode 2）

4 结论

本文提出了不平衡电压条件下DFIG 的H-DPC策略。该控制策略在两相静止坐标系下构建有功功率、无功功率的调制电压，可在无需锁相矢量定向的情况下实现对有功功率、无功功率的无差跟踪。同时，通过常规功率理论和拓展功率理论的组合，构造了可消除有功功率／无功功率2 倍频波动分量和负序定子电流的混合功率反馈量，避免了DFIG定／转子电流的正、负序分离与提取，实现了既定的运行控制目标，增强了DFIG在不平衡电压条件下的运行能力。最后，通过硬件在环实验验证了所提H-DPC 策略的有效性。

附录见本刊网络版（http：//www.epae.cn）。