基于场景概率驱动的输电网和储能分布鲁棒规划

郑晓东，陈皓勇，段声志，黄剑平

（华南理工大学 电力学院，广东 广州 510641）

0 引言

在碳达峰、碳中和的目标要求下，我国走上了以风电、光伏等可再生能源为主的绿色清洁能源发展道路。高比例可再生能源并网将是未来电力系统的基本特征［1］。然而，可再生能源发电具有间歇性、波动性和随机性，大规模可再生能源发电给电力系统的规划带来了更多的不确定性。随着风电、光伏发电的装机容量不断提高，大规模可再生能源并网带来的电力电量不平衡问题日益凸显，这不仅需要输电网解决电力电量平衡问题，还需要提高系统的灵活调节能力。储能可以实现大规模可再生能源的能量转移［2］，有助于提升系统的运行灵活性。根据国家能源局发布的《关于加快推动新型储能发展的指导意见》［3］，到2025年我国储能总装机规模预计达到3×107kW 以上，新型储能将成为能源领域实现碳达峰和碳中和的关键支撑之一。

准确刻画大规模可再生能源的不确定性是制定有效应对可再生能源不确定性的输电网和储能规划方案的关键。目前，考虑可再生能源不确定性的优化方法主要包括随机优化、鲁棒优化、分布鲁棒优化。其中，随机优化假设可再生能源出力满足某一特定的概率分布（如Gauss分布、Weibull分布等），通过选取实际运行中的大量典型场景进行优化。文献［4］采用场景树对风电出力的随机场景进行刻画，以日运行成本最小化为目标进行储能配置；文献［5］以机会约束形式限制弃风率，建立了不同风电利用水平下储能配置的随机优化模型。随机优化选取的场景数量庞大，需要消耗大量的计算资源和时间，效率较低。且当选取的概率分布与实际分布相差较大时，采用随机优化所得规划方案的经济性较差。鲁棒优化无需考虑随机变量的统计信息，只需获取随机变量的区间信息，能够考虑到随机变量在区间内所有可能出现的情况。文献［6］针对源荷的长期不确定性和可再生能源出力的短期不确定性带来的影响，构建了输电网扩展与储能配置的联合规划模型；文献［7］考虑火电机组逐步退出运行的场景，为了消纳大规模风电对储能配置进行规划；文献［8］考虑储能充放电行为对其实际寿命的影响，建立了考虑寿命约束的储能鲁棒规划模型；文献［9］建立了考虑输电网结构优化的输电网与储能联合鲁棒规划模型；文献［10］以提升配电网的日平均灵活性水平最优为目标，建立了考虑源网荷灵活性资源的配电网储能鲁棒规划模型；文献［11］以一系列的风电出力离散场景集作为不确定集，建立了电网侧储能的鲁棒配置模型，所得规划方案能够确保不发生弃风和切负荷。但根据大数定律，极端场景实际发生的概率很低，由于不确定集中没有利用风电出力的历史信息，鲁棒优化所得结果过于保守且经济性较差。分布鲁棒优化综合了随机优化和鲁棒优化的特点，通过随机变量的历史数据来构建概率分布模糊集，在所构建的概率分布模糊集中寻找随机变量最恶劣的概率分布进行优化。分布鲁棒优化既能够考虑随机变量的历史信息，又具有一定的鲁棒性，已经在最优潮流、发电备用、无功优化、储能规划等研究中得到应用。文献［12］利用数据样本构建刻画风光不确定性的Wasserstein 球，建立了含多类型电源的动态最优潮流模型；文献［13］利用发电机组和输电线路随机故障率的矩信息，建立了考虑N-K安全准则的日前机组组合模型；文献［14］基于主元分析方法建立风电出力的降维模糊集，构建了考虑风电不确定性和相关性的多区域电网分布鲁棒经济调度模型；文献［15］考虑分布式电源的典型出力场景，建立了数据驱动下的主动配电网无功优化模型；文献［16］采用Kullback-Leibler 散度对风电出力的不确定性进行刻画，建立了以弃风率为机会约束的风电场储能容量配置优化模型，但需要对非凸的机会约束进行近似凸化处理；文献［17］利用Wasserstein 测度刻画风电出力的不确定性，建立了风-氢混合系统的储能容量分布鲁棒优化配置模型。然而，基于场景概率驱动的分布鲁棒优化方法在输电网和储能联合规划方面的应用研究尚未见报道。

基于上述分析，本文利用风电出力的历史数据构建基于L1-范数和L∞-范数的概率分布不确定集，进而建立基于场景概率驱动的输电网和储能分布鲁棒联合规划模型。本文构建的模型为min-max-min 3 层鲁棒优化问题，采用可并行计算的列和约束生成C&CG（Column-and-Constraint Generation）算法在求解max-min 优化问题时可以将其转化为能并行计算的线性规划问题。以Graver 6节点系统为算例验证所建模型和算法的有效性与实用性，并分析风电接入水平、储能投资成本等因素对输电网和储能联合规划结果的影响。

1 考虑风电接入的输电网和储能联合规划

1.1 目标函数

本文以等年值投资成本和运行成本之和（即年综合成本）最小为目标进行输电网扩展和储能配置联合规划，其中等年值投资成本包括输电线路和储能的等年值投资成本，运行成本包括火电机组的燃料费用、弃风及切负荷带来的惩罚费用。目标函数可表示为：

式中：C为系统的年综合成本；Cinv为系统的等年值投资成本；Coper为系统的运行成本；σ为等年值投资成本与运行成本之间的等值因子，取值为365；Cbes，inv为储能的等年值投资成本，一般考虑由容量成本和功率成本两部分组成；Cline，inv为新建输电线路的等年值投资成本；r为贴现率；TBES为储能的经济使用年限；ΩBES为储能的安装节点集合；分别为节点i处储能的单位容量、单位功率投资成本；Ei、Pi分别为节点i处储能的配置容量、配置功率；Tline为输电线路的经济使用年限；Kij、分别为走廊通道ij可存线路、已有线路集合；Ωline为输电线路走廊通道集合；cij，k为走廊通道ij建设第k条输电线路所需费用；xij，k为走廊通道ij建设第k条输电线路的投资决策变量，若建设线路则取值为1，否则取值为0；T、Ng、NB分别为调度时段、火电机组、系统节点数量；C(Pg，t)为时段t火电机组g的燃料费用，一般用式（6）所示二次函数表示，为了简化计算，可采用分段线性函数近似表示；Pg，t为时段t火电机组g的发电功率分别为节点i处单位弃风、单位切负荷的惩罚费用；ΔPWi，t、分别为时段t节点i的弃风量、切负荷量；ag、bg、cg分别为火电机组g燃料费用二次函数的二次项、一次项、常数项系数。

1.2 约束条件

联合规划模型考虑的约束条件主要包括输电网和储能的投资决策约束及给定投资决策下的运行约束。

1.2.1 投资决策约束

1）储能的投建约束。

受限于地理空间、社会经济条件等多方面因素，安装储能的节点数量是有限的，需满足如下约束：

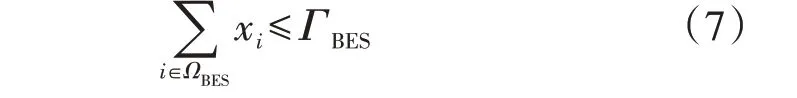
式中：xi为节点i处安装储能的投资决策变量，若安装则取值为1，否则取值为0；ΓBES为允许安装储能的最大节点数量。

节点i处储能的配置容量、配置功率满足如下约束：

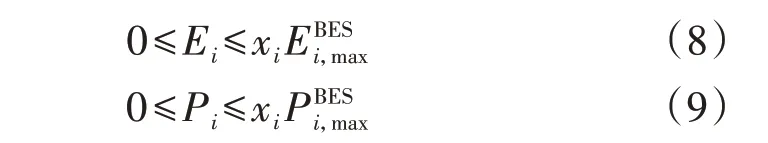
节点i处储能在运行阶段储电量的下限Ei，min、上限Ei，max与配置容量Ei之间的关系分别为：

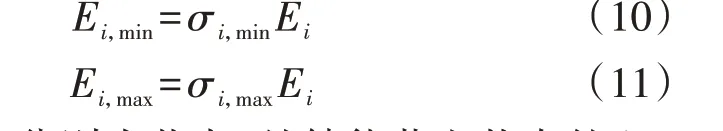
式中：σi，max、σi，min分别为节点i处储能荷电状态的上、下限。

2）输电线路投建约束。

对于走廊通道相同的输电线路而言，其需满足如下序列建设约束：

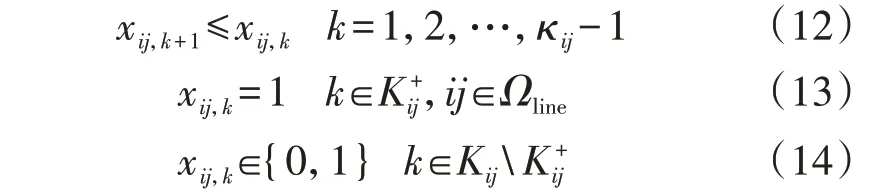
式中：κij为走廊通道ij可存线路的最大数量。式（12）表示当走廊通道ij不建设第k条输电线路时，第k+1—κij条输电线路均不被建设，只有当第k条输电线路被建设时，第k+1条线路才有可能被投建。

每个走廊通道允许建设的输电线路数量是有限的，需要满足走廊通道输电线路数量约束：

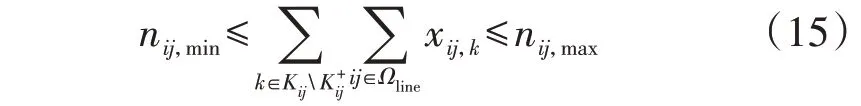
式中：nij，min、nij，max分别为走廊通道ij允许建设输电线路数量的最小值、最大值。

除了需满足输电线路和储能各自的投建约束外，还应满足输电网和储能联合规划的总投资成本约束：

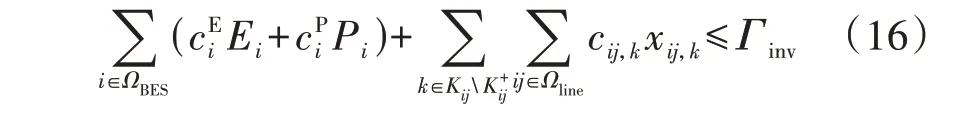
式中：Γinv为用于输电线路和储能联合规划的最大投建费用。

1.2.2 运行约束

系统的运行约束主要包括火电机组的运行约束、储能的运行约束、节点功率平衡约束、节点电压相角约束、输电线路潮流约束、弃风量约束、切负荷量约束、旋转备用约束。

1）火电机组的运行约束。

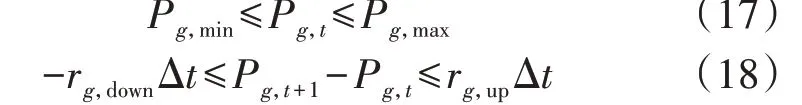
式中：Pg，max、Pg，min分别为火电机组g发电功率的上、下限；rg，up、rg，down分别为火电机组g的向上、向下爬坡速率限值；Δt为时段间隔，本文取值为1 h。

2）储能的运行约束。

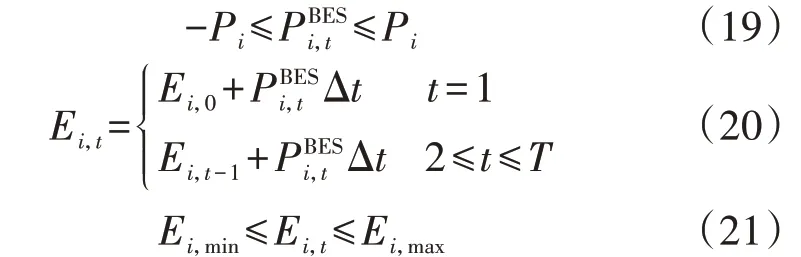
3）节点功率平衡约束。

式中：Gi为位于节点i处的火电机组集合为时段t节点i处风电场的有功出力为时段t节点i的负荷；Lfrom(i)、Lto(i)分别为首节点是i、末节点是i的支路集合；fij，k，t为时段t走廊通道ij第k条线路传输的有功功率。

4）节点电压相角约束。

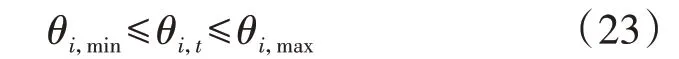
式中：θi，t为时段t节点i的电压相角；θi，max、θi，min分别为节点i电压相角的上、下限。

5）输电线路潮流约束。

输电线路潮流约束需要分别考虑系统中的已有线路和备选线路。对于系统中的已有输电线路而言，需满足：

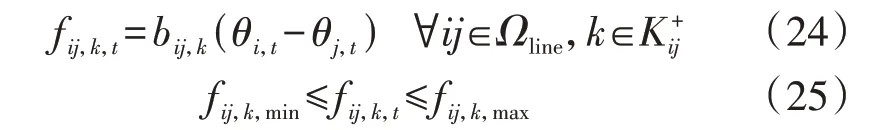
式 中：bij，k为 走 廊 通 道ij第k条 输 电 线 路 的 电 纳 值；fij，k，max、fij，k，min分别为流经走廊通道ij第k条输电线路有功功率的上、下限。

对于系统中的备选输电线路而言，需满足：

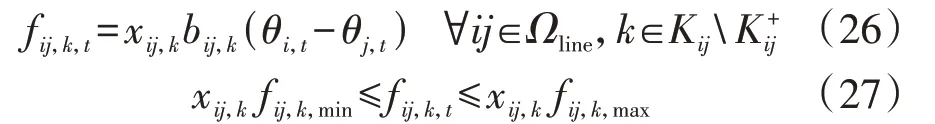
式（27）表明：当备选输电线路没有被投建时，流经该线路的有功功率为0；当备选输电线路被投建时，流经该线路的有功功率不超过线路容量。由于式（26）存在双变量的乘积项，需要将其转化为线性约束，如式（28）所示。

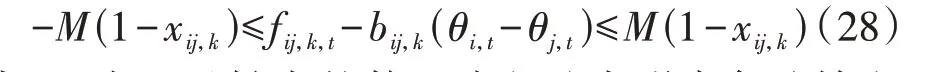
式中：M为一足够大的数。式（28）表明当备选输电线路被投建时满足直流潮流方程。

6）弃风量约束。

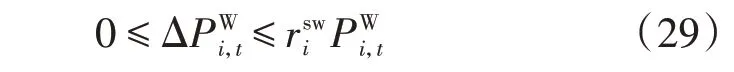
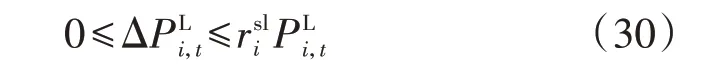
8）旋转备用约束。

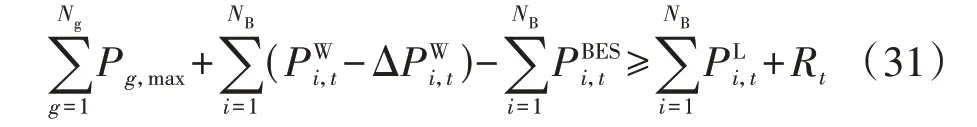
式中：Rt为时段t系统的旋转备用容量，本文设置旋转备用容量为负荷的10%。

2 风电出力场景概率不确定集的构建

假设存在Z个风电出力历史场景，通过聚类方法可以得到K个离散的典型场景，即典型场景集合S={S1，S2，…，SK}。第s个典型场景Ss（s=1，2，…，K）包含的历史场景数量为Ms，则所有典型场景构成的风电出力典型场景的初始概率分布P0=[，]，其中=Ms/Z（s=1，2，…，K）为第s个典型场景发生的概率。但是由于风电出力存在随机性，实际概率分布P与基于历史数据的初始概率分布P0之间有所偏差。因此，本文基于L1-范数和L∞-范数构建概率分布不确定集来刻画风电出力典型场景实际发生的概率，分别如式（32）和式（33）所示。

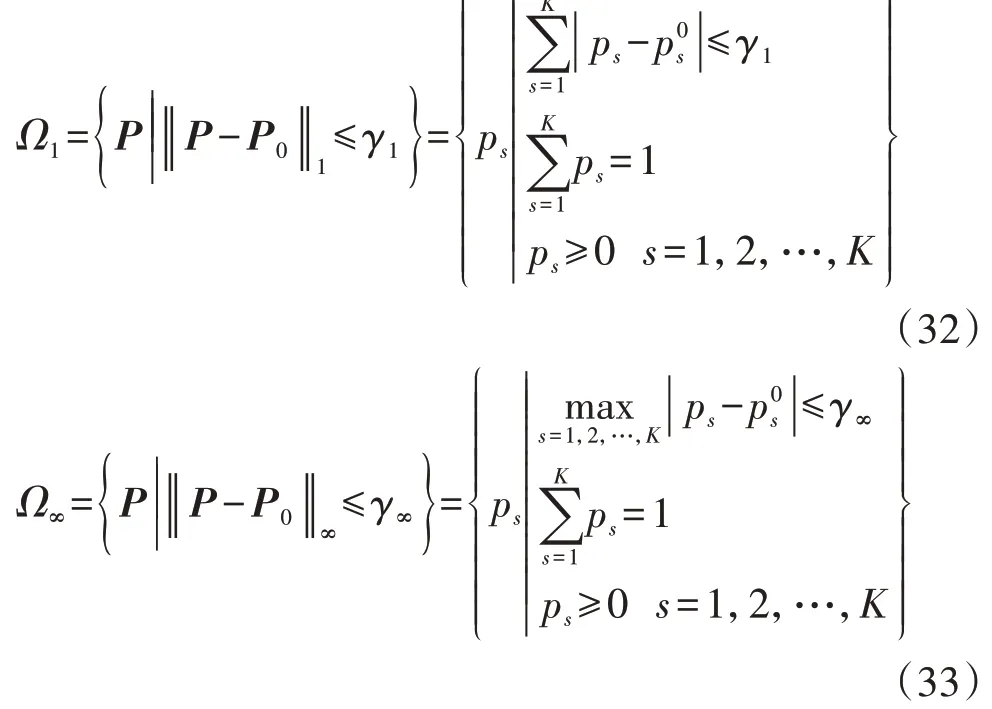
式中：Ω1、Ω∞分别为L1-范数、L∞-范数概率分布不确定集；ps为第s个典型场景实际分布对应的概率；γ1、γ∞分别为L1-范数、L∞-范数约束下风电出力场景概率分布波动的预算不确定度。L1-范数和L∞-范数概率分布不确定集从2 个不同的角度对风电出力场景的概率分布波动程度进行刻画：L1-范数概率分布不确定集从所有场景概率分布总的波动程度对风电出力场景概率的不确定性进行刻画，而L∞-范数概率分布不确定集从所有场景概率分布的最大波动程度对风电出力场景的不确定性进行刻画。

因此，基于L1-范数和L∞-范数对风电出力场景的实际概率与初始概率之间的偏差进行刻画，得到风电出力场景的混合概率分布不确定集Ω为：

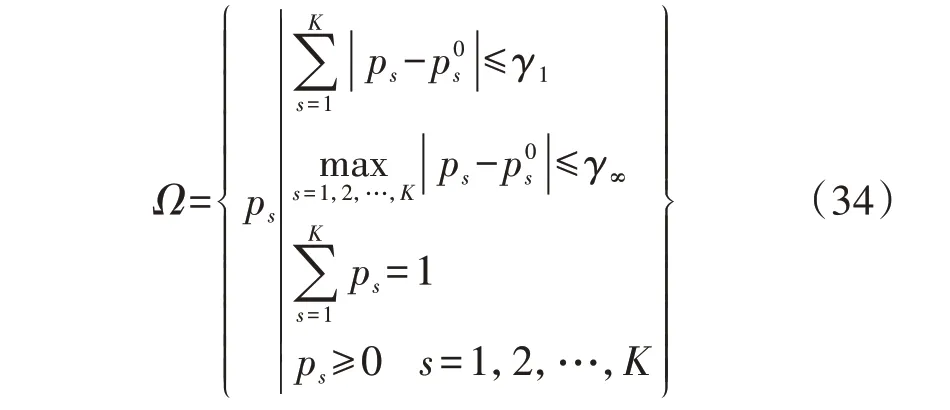
随着γ1、γ∞的增大，模型所能适应的风电出力场景概率分布的波动程度也增大，模型的鲁棒性增强。因此，应该寻找合理确定输电网和储能规划保守性的γ1和γ∞的方法。

由文献［18］可知，风电出力场景发生的概率满足式（35）。

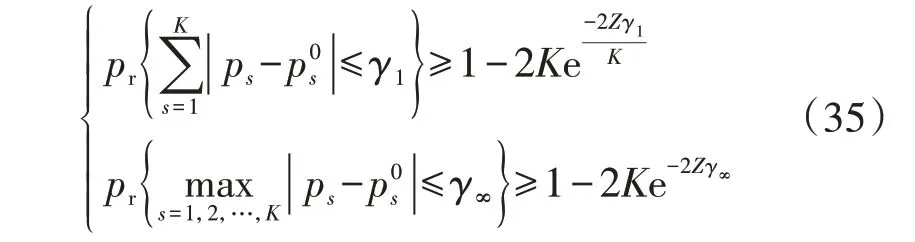
根据式（36）可知，当考虑足够多的风电历史数据时，预算不确定度趋近于0，此时风电出力场景的L1-范数和L∞-范数概率分布不确定集包含的概率分布趋近于风电出力场景的实际概率分布。

3 基于场景概率驱动的输电网和储能分布鲁棒联合规划

基于历史数据得到的初始概率分布与实际概率分布之间存在偏差。因此，根据第2 节构建的概率分布不确定集，本节构建了基于场景概率驱动的输电网和储能两阶段分布鲁棒联合规划模型。阶段1旨在寻找年综合成本最小的输电网和储能投资决策，阶段2 旨在在给定的输电网和储能规划方案下以运行成本最小化为目标进行系统运行模拟。基于场景概率驱动的输电网和储能分布鲁棒联合规划模型的矩阵形式为：

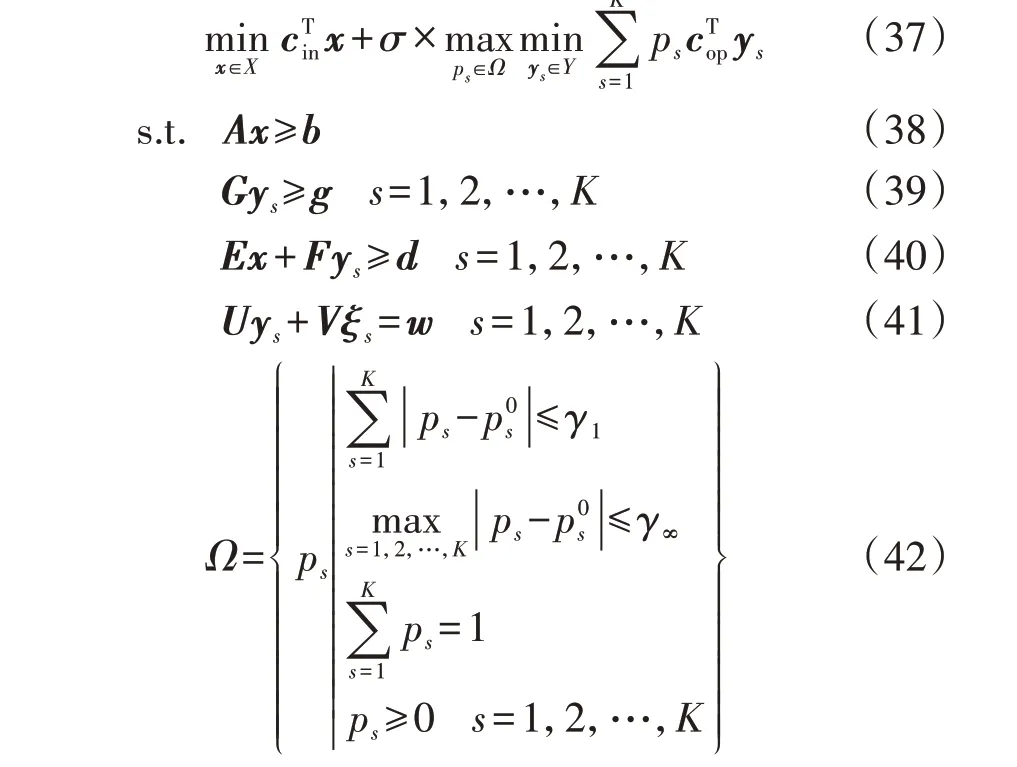
式中：x为阶段1 的决策变量，包括新建输电线路的走廊通道和数量、安装储能的位置以及配置容量和配置功率；X为输电网和储能的投资决策变量集合；ξs为风电历史出力场景经聚类后得到的第s个典型出力场景；Y为给定输电网和储能规划方案以及风电出力场景概率分布下的系统运行决策变量集合，包括火电机组的发电功率、储能的充放电功率等；为输电线路和储能的等年值投资成本为在给定的输电网和储能规划方案下，概率分布不确定集中最恶劣概率分布对应的运行成本期望值，包括火电机组的燃料费用、弃风及切负荷带来的惩罚费用；A、b、G、g、E、F、d、U、V、w为相应的系数矩阵。模型的约束条件包含3 类：第1 类约束条件（式（38））为阶段1投资决策相关约束，具体包括1.2.1节的式（7）—（16）；第2 类约束条件（式（39）和式（41））为阶段2 运行决策相关约束，具体包括1.2.2 节的式（17）、（18）、（20）、（22）—（25）、（29）—（31）；第3 类约束条件（式（40））为阶段1 与阶段2 决策变量之间的耦合约束，具体包括式（19）、（21）、（27）、（28）。本文构建的基于场景概率驱动的输电网和储能两阶段分布鲁棒联合规划模型属于min-max-min 3 层鲁棒优化问题，外层进行年综合成本最小的输电网和储能投资决策，中间层寻找K个典型场景的最恶劣概率分布，内层在给定投资决策和最恶劣概率分布的情况下，寻找运行成本期望值最小的运行决策变量。

由于风电出力具有一定的随机性，其概率分布呈现“尖峰厚尾”的分布特征［19］。因此，难以用特定的概率分布函数对风电出力进行准确刻画。本文所建模型无需依赖于特定的概率分布（如正态分布、Weibull 分布等），只需获取风电出力的历史信息，这样能够改善鲁棒优化保守性过强的问题。

4 模型转化和求解

4.1 混合概率分布不确定集的等价转化

由于构建的概率分布不确定集存在绝对值不等式约束，无法直接求解。可通过下述转化过程，将L1-范数和L∞-范数概率分布绝对值不等式约束转化为线性约束。

对于L1-范数概率分布约束而言，引入辅助变量，可将其转化为以下线性约束：

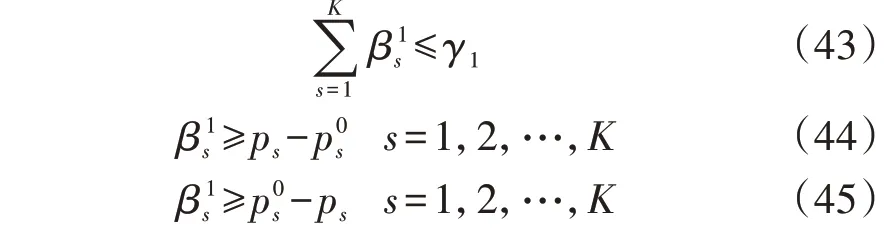
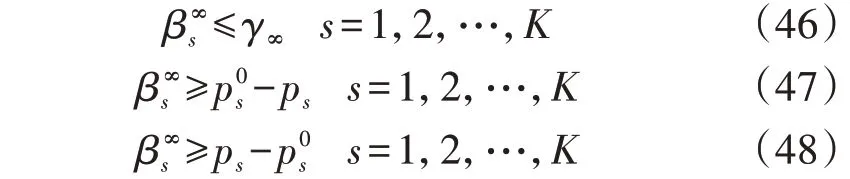
因此，混合范数概率分布不确定集被转化为：

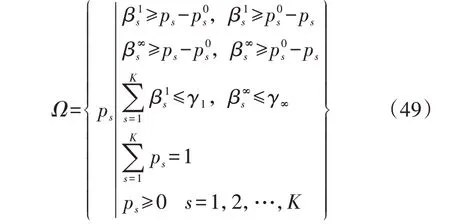
4.2 模型求解

本文构建的基于场景概率驱动的输电网和储能两阶段分布鲁棒联合规划模型是min-max-min 3 层鲁棒优化问题，通常采用Benders 分解算法［20］和C&CG 算法［21］进行求解，在求解时将原问题拆分为主问题和子问题进行交替迭代计算。当采用Benders 分解算法求解min-max-min 3 层鲁棒优化问题时，需要对内层模型进行对偶转换并对中间层进行合并，由于对偶转换过程复杂，且在转换过程中会出现高度非凸的双线性项，从而影响模型的收敛性和求解速度，求解效率不高。所建模型的max-min 内层优化问题具有可并行计算的特殊性，且C&CG 算法比Benders分解算法具有更快的收敛速度，因此本文采用可并行计算的C&CG 算法求解该模型。当采用C&CG 算法时，无需进行对偶转换，且能避免出现复杂的非线性项，将min-max-min 3层鲁棒优化问题转化为混合整数规划主问题和可并行计算的线性规划子问题。模型求解流程图如图1 所示，具体步骤和变量说明见附录A。

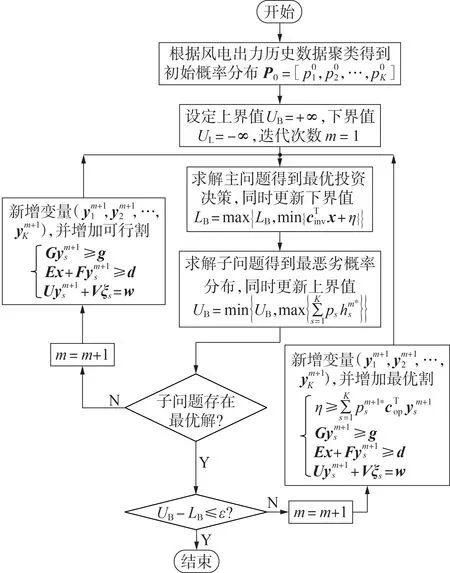
图1 基于C&CG算法的模型求解流程图Fig.1 Flowchart of solving model based on C&CG algorithm

5 算例分析

5.1 算例简介

本文以Garver 6 节点系统［22］为算例进行仿真计算，系统拓扑结构见附录B 图B1。该系统共有2 台火电机组，分别位于节点1和节点3。每台火电机组的装机容量为400 MW，1 h 的爬坡功率为装机容量的50%。储能采用磷酸铁锂电池。系统输电线路参数和拟安装储能的基本参数分别见附录B 表B1 和表B2。设定贴现率为10%，投资回收周期为10 a。输电线路的造价参照文献［23］取值。单位弃风、切负荷的惩罚费用分别为1 000、40 000 元／（MW·h）。在节点2、节点6处分别接入装机容量为250、200 MW的风电场。基于200 个历史场景数据采用K-means聚类得到风电出力典型场景。设定典型场景数量K=8，置信度α1=α∞=99.99%。系统的年最大负荷为780 MW，总装机容量为1250 MW。采用MATLAB编写模型程序，调用CPLEX 求解器进行求解。运行环境为Core i5-8250U 1.60 GHz，内存为8 GB。

5.2 不同风电接入水平对规划结果的影响

根据《中国可再生能源发展报告2020》，到2025年我国可再生能源发电装机将占总发电装机的50%以上。高比例可再生能源并网势必会给电力系统的运行规划带来较大的影响。显然，为了减少风电资源的浪费，不同的风电接入水平要求系统具有不同的风电接纳能力。定义风电接入水平ς为风电容量与初始设定风电容量的比值，则不同风电接入水平下的规划结果如表1所示。

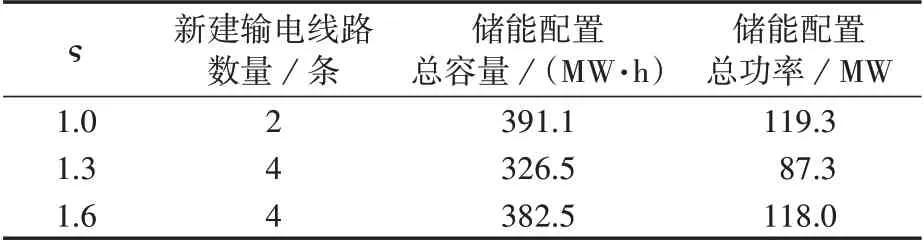
表1 不同风电接入水平下的规划结果Table 1 Planning results under different wind power access levels

由表1 可知，在输电网和储能联合规划中，系统需要配置的储能容量和功率与风电接入水平并不呈现简单的线性增加关系。当风电接入水平逐步增大时，系统需要通过新建输电线路和配置储能相互配合，同时提升风电的外送能力和系统的灵活调节能力以实现更好的运行经济性。

5.3 储能投资成本对规划结果的影响

由于现有技术条件的限制，储能投资成本仍较高，这将显著影响大规模储能的选址定容结果。为了探究储能投资成本对规划结果的影响，引入储能成本系数α，将储能的等年值投资成本表示为：

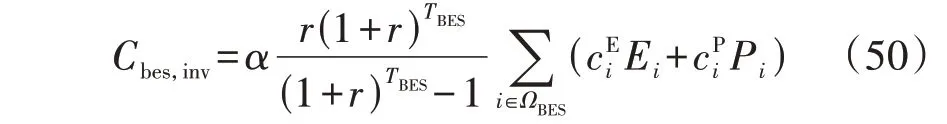
设定储能成本系数α取值分别为0.6、1.0、1.4，所得规划结果如表2 所示。由表可以知道，随着储能成本系数α减小，系统的年综合成本降低。这是因为系统配置储能容量和功率的增大，使得系统的风电接纳能力增强，从而提升了系统的运行经济性，因此储能成本系数对规划结果有影响的显著。当储能成本系数较大时，相较于配置更多容量的储能，新建输电线路能够获得更好的运行经济性；当储能成本系数较小时，配置储能可以起到延缓输电线路建设的作用。

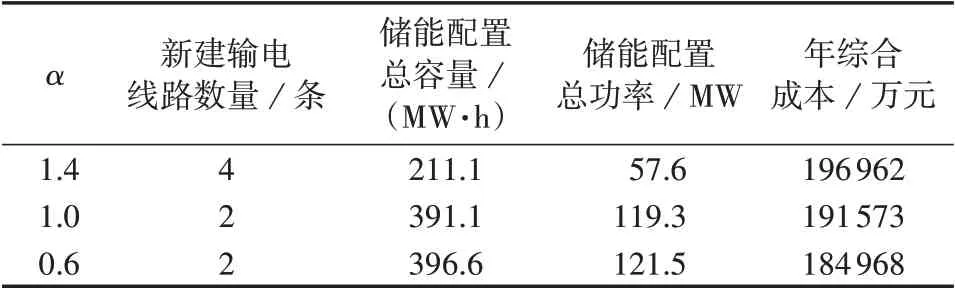
表2 不同储能成本系数下的规划结果Table 2 Planning results under different energy storage cost coefficients

5.4 不同优化方法所得的计算结果

为了对比本文所用分布鲁棒优化方法与其他优化方法所得规划方案，保持Garver 6 节点系统的基本参数不变，分别采用随机优化方法与传统鲁棒优化方法进行计算，所得规划结果如表3所示。

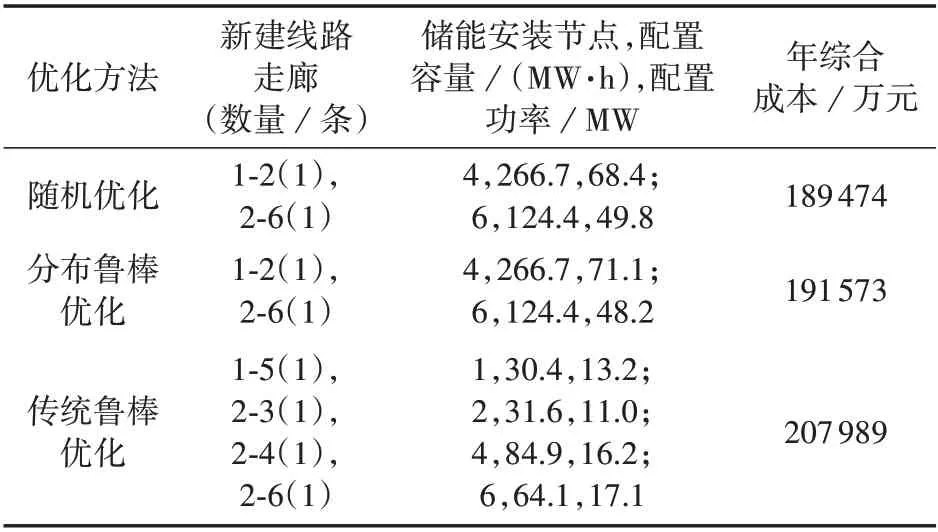
表3 不同优化方法所得计算结果Table 3 Calculative results of different optimization methods

由表3 可知：由于随机优化方法基于给定的风电出力场景进行优化决策，没有考虑风电出力场景的实际概率分布与初始概率分布之间的偏差，所得规划方案的经济性较好但保守性较弱；而传统鲁棒优化方法仅在考虑风电出力波动的最恶劣场景下进行决策，但是根据大数定律，波动区间内的最恶劣场景发生的概率往往很小，所以传统鲁棒优化方法所得规划方案的保守性较强但经济性较差；本文所用分布鲁棒优化方法能够在考虑概率分布不确定集内的最恶劣概率分布下进行决策，且能通过修改概率分布不等式的置信度和用于构建概率分布不确定集的历史数据规模对预算不确定度进行调整，能够在考虑风电出力随机波动性的同时，在概率分布不确定集内具备一定的鲁棒性。因此，本文所提基于场景概率驱动的输电网和储能分布鲁棒联合规划模型能够在投资决策的经济性和保守性之间实现较好的折中。此外，设置α1=α∞得到系统年综合成本与预算不确定度γ∞之间的关系曲线如图2所示。

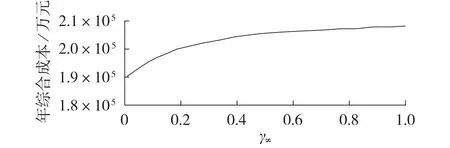
图2 年综合成本与γ∞之间的关系曲线Fig.2 Relationship curve of annual comprehensive cost vs. γ∞

由图2可知，随着γ∞增大，系统年综合成本也增大。这是因为当预算不确定度不断增大时，规划模型考虑的风电出力场景概率分布的波动程度不断增大，当概率分布不确定集的预算不确定度γ∞增大至一定的程度时，本文模型所得规划方案的年综合成本接近于传统鲁棒优化方法所得方案的年综合成本。

5.5 混合范数与单一范数的优化结果对比

为了对比采用混合范数（同时考虑L1-范数和L∞-范数）和单一L1-范数的计算结果，取α1=0.6、α∞∈[0.5，0.8]进行计算，所得优化结果如表4 所示。同理，为了对比采用混合范数和单一L∞-范数的计算结果，取α∞=0.9、α1∈[0.40，0.95]进行计算，所得优化结果如表5所示。

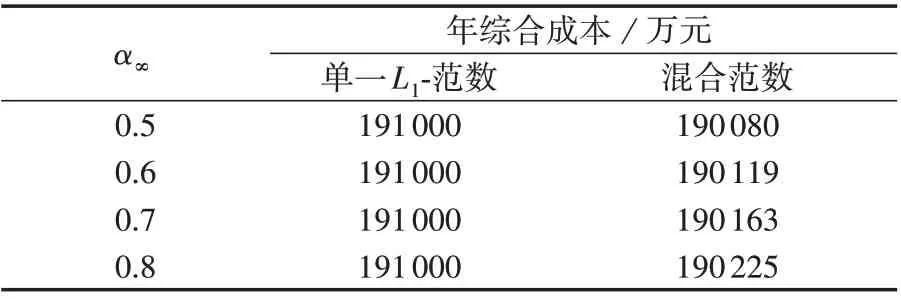
表4 混合范数与单一L1-范数的优化结果对比Table 4 Comparison of optimization results between combined norm and single L1-norm

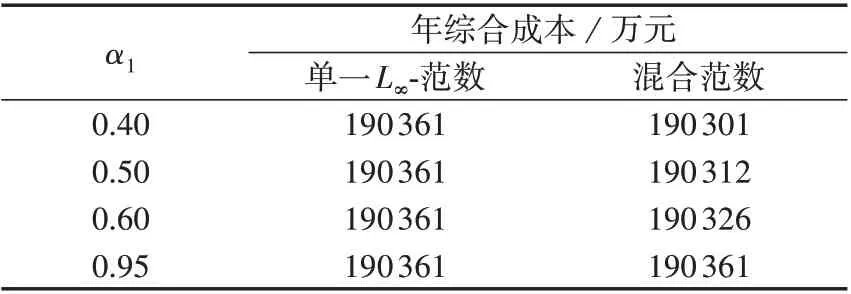
表5 混合范数与单一L∞-范数的优化结果对比Table 5 Comparison of optimization results between combined norm and single L∞-norm

由表4 和表5 可知：相比于采用单一范数，采用混合范数所得规划方案的年综合成本更低，表明采用混合范数相比单一L1-范数、单一L∞-范数更能降低决策的保守性，从而获得更优的经济性结果；当α1=0.95 且α∞=0.9 时，采用L∞-范数和混合范数所得年综合成本结果相同，这说明当L1-范数约束条件的置信度足够大时，L∞-范数概率分布约束条件对风电出力场景概率分布波动的影响更大。

5.6 历史数据规模对规划结果的影响

为了探究用于构建概率分布不确定集的历史数据规模对规划结果的影响，在设置的典型场景数量K、置信度α1和α∞不变的情况下，采用不同规模的历史数据进行计算，所得结果如表6 所示。由表可知，随着历史数据规模的增大，所得规划方案的年综合成本有所降低，这是因为随着历史数据规模的增大，概率分布不确定集的预算不确定度减小，概率分布不确定集包含的概率分布越来越接近于实际概率分布，这有利于降低规划决策的保守性。

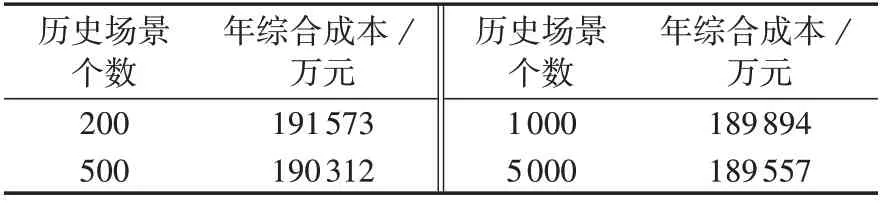
表6 不同历史数据规模下的计算结果Table 6 Calculative results under different historical data scales

典型场景数量K、历史场景数量Z与置信度α1和预算不确定度γ1之间的关系分别如附录B 图B2和图B3 所示。由图可知，随着典型场景数量K的增大，概率分布不确定集的置信度α1提高，用于构建不确定集的历史场景数量Z减小，不确定集的预算不确定度γ1增大，这使得模型的保守性得到提升，从而能够应对更大程度的风电场景概率波动，规划人员可以根据对风险的偏好程度对模型的保守性进行适当调整。

5.7 C&CG算法的计算效率分析

为了探究C&CG 算法的计算效率，令α1=α∞并设置不同的置信度，采用C&CG 算法进行计算，所得迭代结果如表7所示。由表可知，本文采用的C&CG算法经过2 次迭代就满足收敛要求，这表明采用可并行计算的C&CG算法具有较高的求解效率。

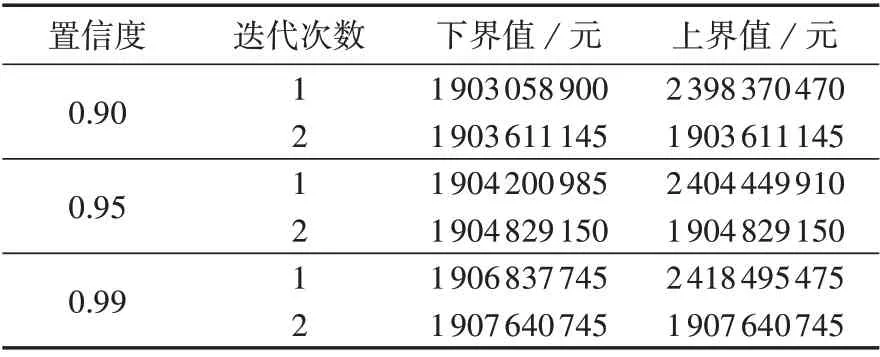
表7 C&CG算法的迭代结果Table 7 Iteration results of C&CG algorithm

6 结论

本文针对大规模风电接入带来的消纳问题，基于风电出力历史数据构建基于L1-范数和L∞-范数的混合概率分布不确定集，进而建立基于场景概率驱动的输电网和储能联合规划模型。该模型能够在风电出力场景概率分布不确定集中寻找最恶劣概率分布进行输电网扩展和储能配置规划。Graver 6 节点系统算例的仿真结果验证了模型和算法的有效性，得到的结论如下。

1）本文所建模型能够融合风电出力的历史信息进行投资决策，所得输电网和储能规划方案相比传统鲁棒优化方法所得方案的保守性降低，且能够考虑风电出力场景的随机波动，综合了随机优化和鲁棒优化的特点。采用可并行计算的C&CG 算法求解模型，无需进行复杂的对偶转换和双线性项计算，提高了求解效率，具有一定的工程实用性。相比单一L1-范数、单一L∞-范数，采用混合范数构建概率分布不确定集能够进一步降低模型的保守性。

2）随着风电渗透率的增大，系统需要通过新建输电线路和配置储能来提升风电的外送能力和系统的灵活调节能力，从而进一步消纳风电。储能投资成本系数对输电网和储能规划结果的影响显著，随着储能投资成本系数减小，配置储能能够进一步提升风电消纳能力，降低系统的运行成本。

附录见本刊网络版（http：//www.epae.cn）。