基于磁环的输电线路雷击过电压抑制方法

周利军，胡 琛，黄 林，王东阳，吴统帅，张 栋，陈斯翔

（1. 西南交通大学 电气工程学院，四川 成都 611756；2. 广东电网有限责任公司 佛山供电局，广东 佛山 528000）

0 引言

随着我国电力系统的迅速发展，输电线路长度不断增加，穿过雷击频繁、土壤电阻率高的地区的线路越来越多。根据电网的运行数据，绝大多数的输电线路跳闸事故是由雷击造成的，雷击引起的输电线路停电每年都给电力系统带来了巨大的经济损失及沉重的检修工作负担［1-4］。

为减少雷击跳闸事故的发生，众多防雷措施被应用到输电线路中，例如通过改造接地装置降低杆塔接地电阻、减小架空地线保护角、架设耦合地线、增加绝缘子片数和安装线路型避雷器等［5-8］，这些防雷措施的雷击防护效果各不相同，但是涉及的防雷改造工程的工程量及难度都较大，对已有输电线路进行防雷改造时容易浪费人力、财力［9］，故目前缺少施工简单且防雷效果较好的方法对已有的雷击跳闸率较高的输电线路进行防雷改造。在电力系统中，相关研究表明磁环可用于特快速暂态过电压（VFTO）的防护［10-17］。文献［10-11］提出利用铁氧体磁环抑制气体绝缘开关（GIS）中VFTO 的方法，并通过低压试验验证了其可能性；文献［12］研究了铁氧体性能参数对抑制VFTO 的影响，并提出一种能达到理想抑制效果的磁环尺寸计算方法；文献［13］利用高压模拟试验研究了3 种磁环材料的VFTO 抑制效果及材料磁饱和影响；文献［14］研究了利用磁环抑制特高压GIS设备中VFTO 的可行性，并对比分析了铁氧体与非晶2 种磁环材料的效果及差异；文献［15-17］利用真型252 kV GIS 试验平台进行高压对比试验，分析磁环的VFTO 的抑制效果及其对VFTO 波形主要参数的影响。考虑到磁环抑制GIS 中VFTO 的效果及VFTO 与雷击过电压有一定相似性（电流幅值大且能量集中在高频）［16］，故此方法对于输电线路防雷有一定的借鉴意义。但与雷击过电压相比，VFTO的波形存在更多大幅振荡，其波头上升时间更短，可以短至几纳秒，因此本文针对磁环抑制雷击过电压的方法开展了相关研究。

本文提出一种基于磁环的输电线路雷击过电压抑制方法：首先采用曲线拟合得到磁环材料的磁化函数，进而基于微元法与电磁场理论计算建立了磁环的磁链计算模型，并利用有限元仿真验证了磁链计算模型的合理性；然后，利用磁环的磁链计算模型在ATP／EMTP中建立了磁环电磁暂态模型，进而分析了不同磁环材料、磁环截面积、磁环长度及磁环形状对磁环抑制雷击过电压效果的影响；最后，利用典型的110 kV 同塔双回输电线路对所提方法进行现场试验。本文方法对于输电线路，特别是已有输电线路，实施相对简单，无须改变线路、杆塔、接地装置的固有结构，将磁环通过人工安装在避雷线上即可。

1 磁环的磁链计算模型

1.1 磁环饱和特性及其磁链计算模型

理论上，磁环能够抑制输电线路雷击过电压，其简易电路原理如图1所示。图中：u为磁环前的电压行波；LR为安装磁环后避雷线相应位置的电感值；Z为磁环后的杆塔波阻抗；uZ为杆塔波阻抗首端电压，其表达式如式（1）所示。

图1 磁环抑制的简易电路原理图Fig.1 Simple circuit diagram of magnetic ring suppression

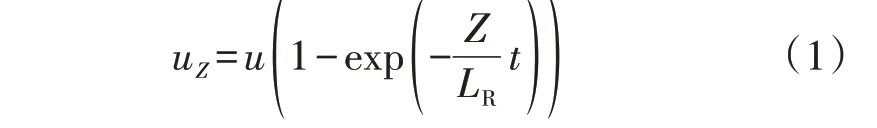
式中：t为时间。

若u为无限长直角波，当其向磁环后传播时，由于电感LR的作用，此时uZ从0 开始按指数规律上升，当t→∞时，uZ的幅值达到u的幅值；若u不是无限长直角波，而是波长很短的电压行波（例如雷击过电压），则能在一定程度上降低uZ的幅值，使uZ的幅值小于u的幅值［18］。

由于雷电流的幅值巨大且其能量主要集中于高频段，所以要求磁环材料具有高磁饱和特性和高工作频率，为此本文选取铁氧体、非晶和铁合金粉芯3种磁环材料，对应的磁化曲线如图2 所示。图中：B为磁感应强度；H为外磁场强度。

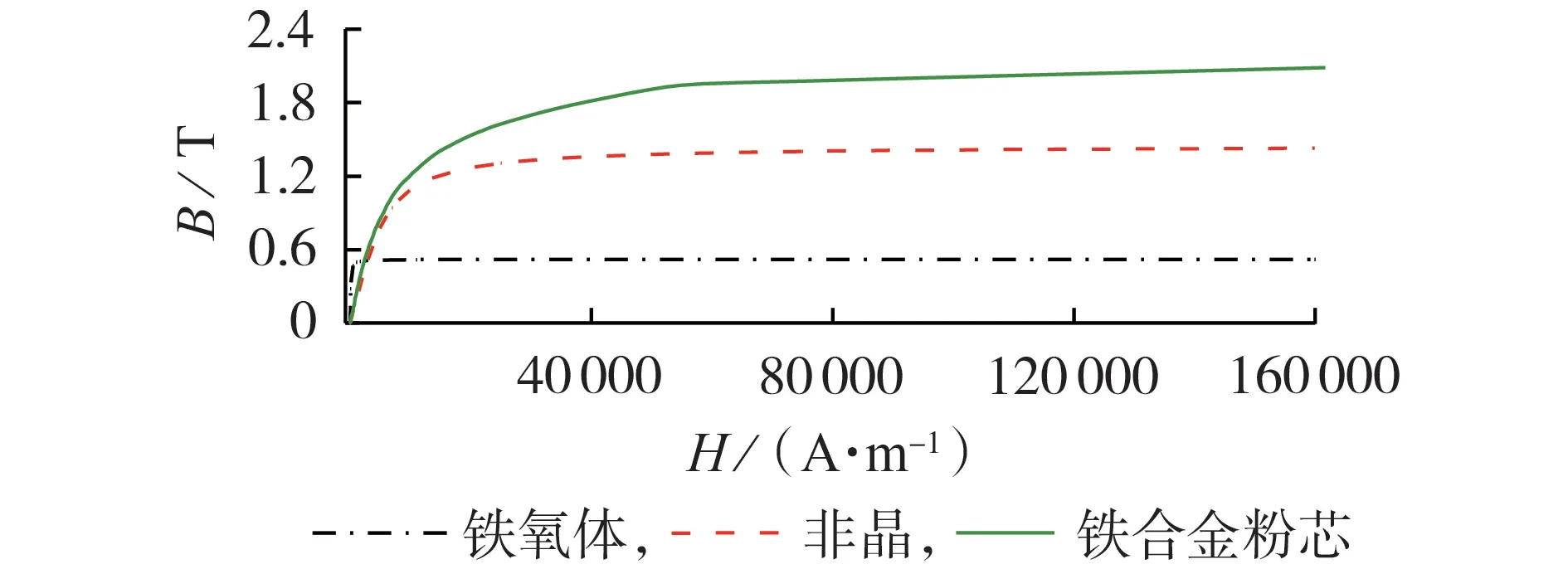
图2 磁环材料的磁化曲线Fig.2 Magnetization curves of magnetic ring materials

当磁环应用于抑制输电线路雷击过电压时，需要承受数千安培甚至数十千安培的雷电流，这必定会使磁环的大部分区域工作在磁饱和状态。文献［19］利用材料的磁导率得到磁环电感模型，而忽略了在大电流下磁环的饱和效应，这将导致雷击暂态响应计算不准确。

为了更加精准地建立适用于雷击时的磁环模型，需考虑磁环材料的饱和特性，即基于材料的磁化曲线建立模型。本文首先采用曲线拟合的方法得到磁环材料的磁化函数，如式（2）所示。

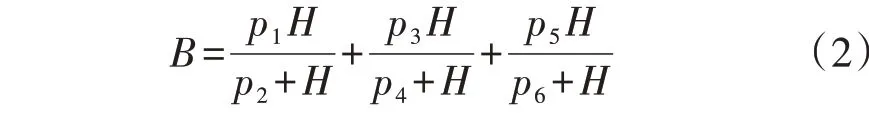
式中：p1—p6为磁环材料的磁化特性参数，具体数值见附录A表A1。

3 种磁化材料的磁化曲线之间存在差异，其中铁氧体材料具有较高的初始磁导率，但是其饱和磁通密度及饱和磁化强度较低，而非晶和铁合金粉芯材料的初始磁导率低，抗饱和性能更高，更适用于大电流下的防护。从表A1 中的拟合结果可知，3 种材料的磁化函数拟合确定系数R2均高于0.999，表明本文的磁化函数对磁环材料的磁化曲线的拟合程度较高。

图3 为磁环模型示意图。图中：I为流经导线的电流大小；l为磁环长度；R1为导线半径；R2、R3分别为磁环内、外半径；dρ为同心微元圆环的环宽；ρ为同心微元圆环内半径；dS为轴向长度为l、宽为dρ的微元矩形；Br为同心微元圆环处磁感应强度大小。本文基于式（2）所示的磁化函数，利用微元法得到考虑磁环饱和特性的磁环磁链计算模型，将磁环区域分为n个环宽为dρ的同心微元圆环（n→∞，dρ→0）。

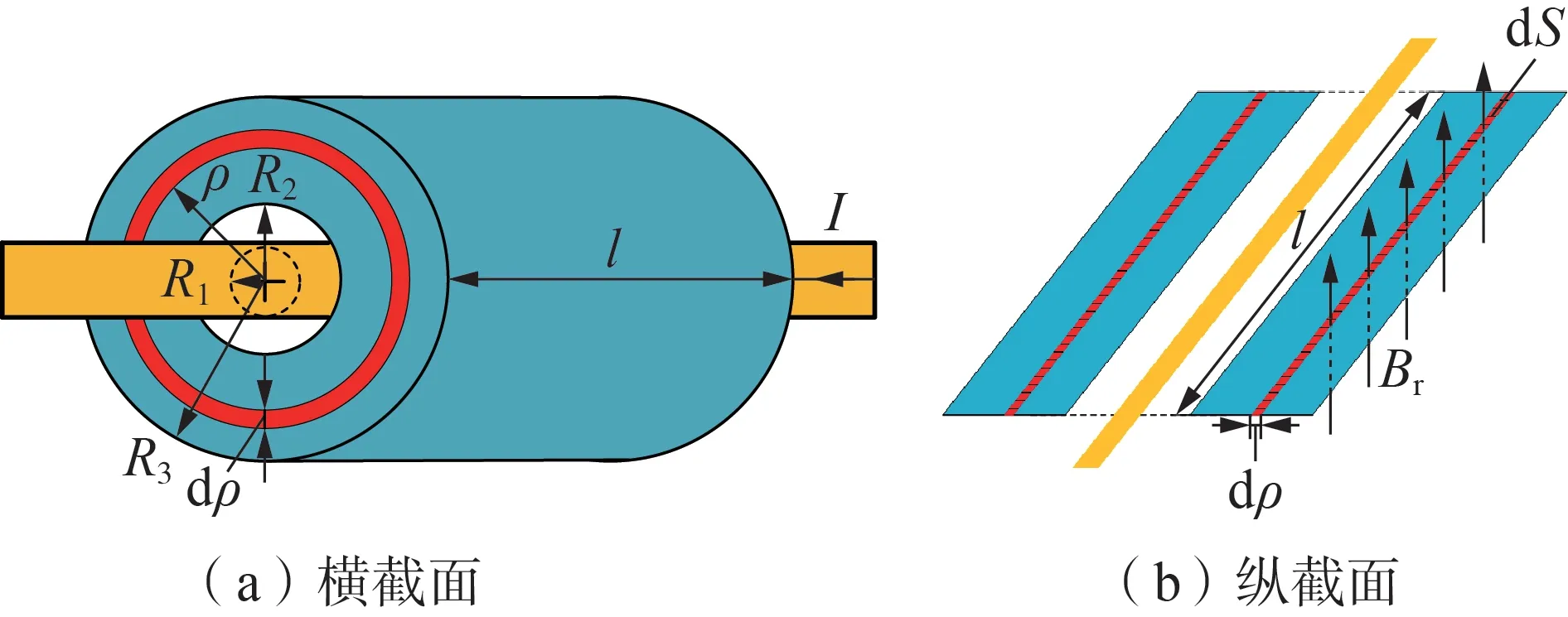
图3 磁环模型示意图Fig.3 Schematic diagram of magnetic ring model

根据安培环路定律可得同心微元圆环处磁场强度大小Hr为：

同心微元圆环处磁感应强度大小Br与其内半径ρ及流经导线的电流大小I相关，将式（3）代入式（2）可得Br如式（4）所示。

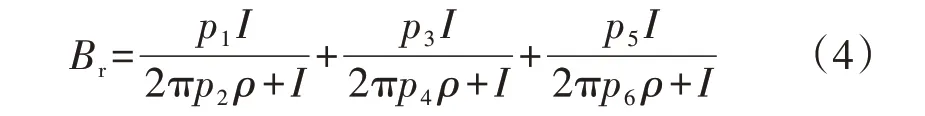
穿过轴向长度为l、宽为dρ的微元矩形的微元磁通dΦr为：

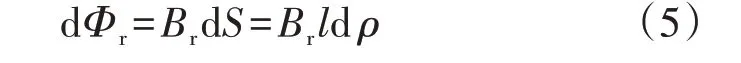
积分可得磁环区域的磁链ψr为：

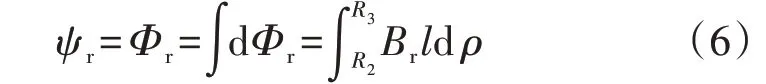
将式（4）代入式（6）计算可得：

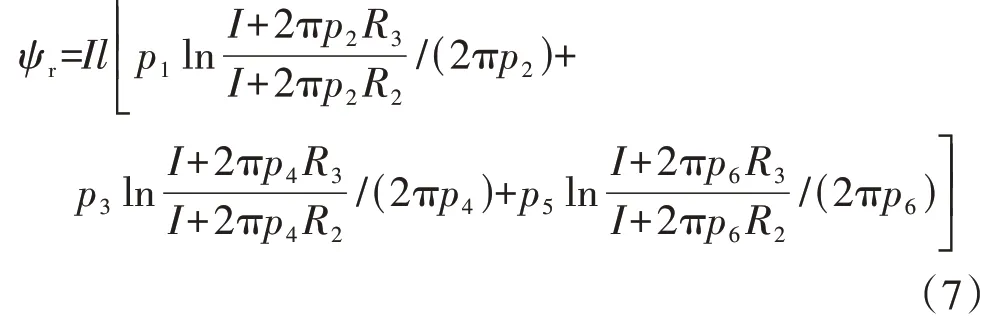
利用同样的方法计算得到导体区域的磁链ψc、气隙区域的磁链ψg分别如式（8）、（9）所示。

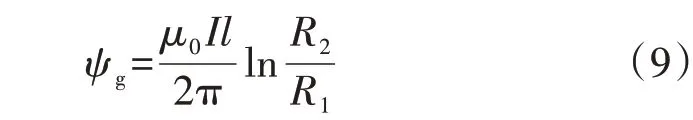
式中：μ0为真空磁导率。

磁环模型的完整磁链ψ包括ψc、ψg和ψr三部分，如式（10）所示。

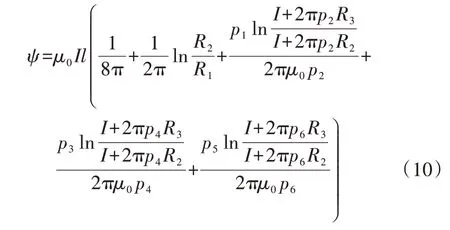
1.2 有限元法仿真验证

为验证磁环的磁链计算模型的正确性，本文采用有限元法FEM（Finite Element Method）进行对比验证。本文采用高精度有限元计算软件COMSOL Multiphysics 建立磁环FEM 模型，如附录A 图A1 所示。模型参数设置为：导线半径为6.18 mm，导线材料为铜；磁环的内、外半径分别为20、40 mm，长度为2 m。利用磁环FEM模型和磁链计算模型得到的3种材料磁环的完整磁链ψ与I的关系曲线如图4所示。

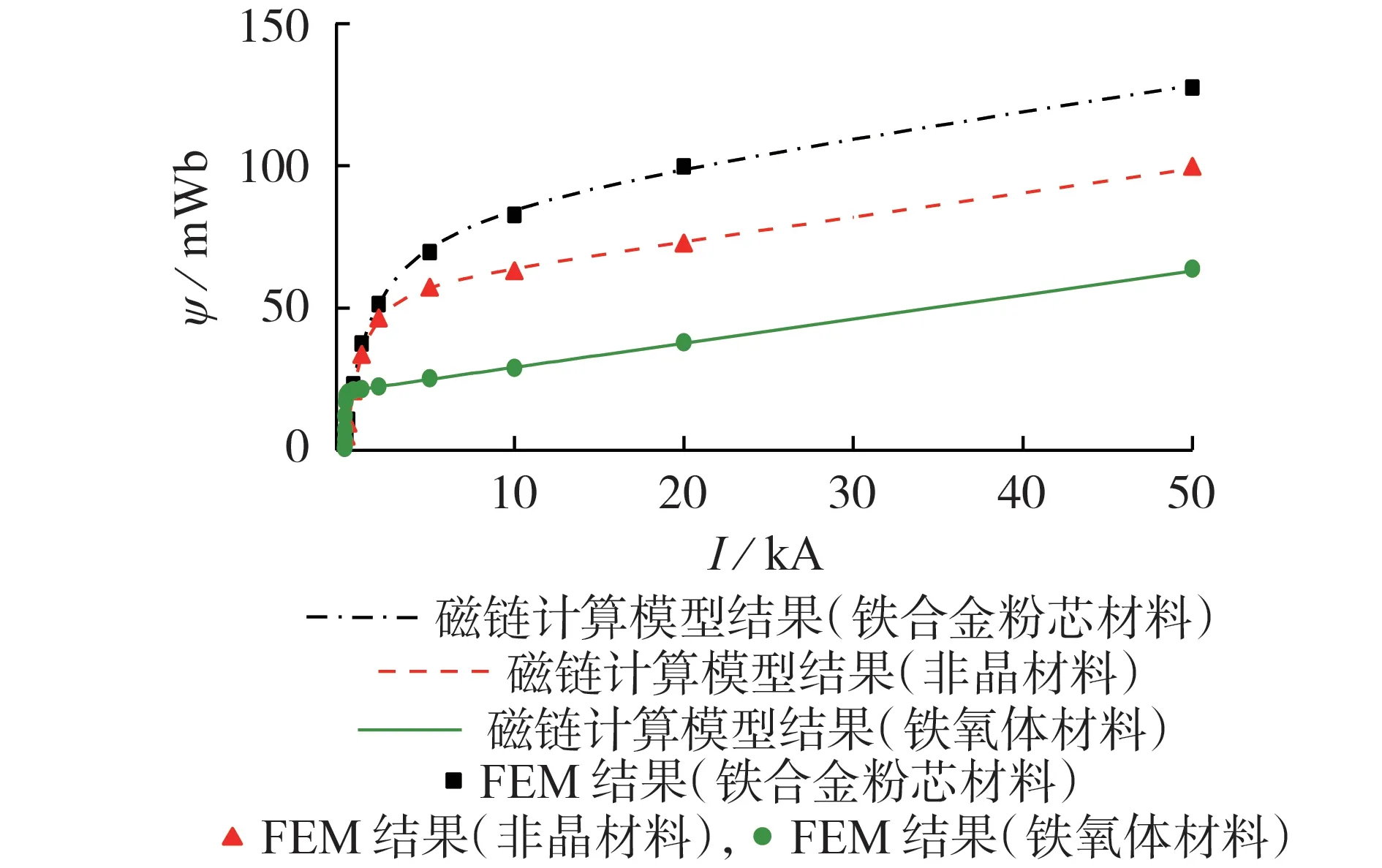
图4 FEM模型与磁链计算模型的计算结果对比Fig.4 Comparison of calculation results between FEM model and flux calculation model

3种材料的ψ-I曲线存在以下异同。

1）相同点：在小电流区域，ψ随着I的增大而急剧增长，曲线较陡，曲线的斜率相对较大且基本不变；当I增大到较大数值后，从磁环半径较小的区域开始出现一定的饱和，使得ψ-I曲线的斜率下降，曲线由陡转平；而在大电流区域，磁环的全部区域已基本饱和，此时ψ-I曲线的斜率也基本不变且数值较小。

2）主要不同点：同样的电流下，3 种材料的完整磁链ψ有所不同；3 种材料的小电流区域、较大电流区域和大电流区域的范围各不相同，铁合金粉芯材料的小电流和较大电流区域比其他2 种材料的范围更广，意味着该材料在同样的电流下更不容易出现饱和现象，雷击过电压抑制效果更好。

FEM模型与磁链计算模型所得结果的误差对比见附录A 表A2。由表可见，对于3 种材料的磁环，FEM模型与磁链计算模型所得结果的平均误差均在2%以内，且最大误差未超过5%。考虑到材料的磁化函数并不能完全拟合材料的磁化曲线，上述误差在可接受范围内，故可以认为本文所提磁环磁链计算模型与FEM 模型所得的结果较为吻合，从而有效验证了磁链计算模型的合理性。

2 磁环应用研究

为研究磁环的输电线路雷击过电压抑制效果，本文基于第1 节的磁环磁链计算模型在电磁暂态仿真软件ATP／EMTP中建立磁环电磁暂态模型，将其应用于110 kV 同塔双回输电线路电磁暂态仿真模型中［20］，分析不同磁环材料（铁氧体、非晶和铁合金粉芯）、磁环截面积、磁环长度以及磁环形状对输电线路防雷效果的影响。

2.1 输电线路电磁暂态模型

本文搭建的110 kV 同塔双回输电线路模型为三基杆塔线路，其示意图见附录A 图A2。将雷击点设置在第一基杆塔与第二基杆塔的档距中央，雷电流采用幅值为20 kA的2.6／50 μs标准波形，雷电流通道的阻抗为300 Ω。在电磁暂态仿真中，可利用非线性电感模拟磁环［21］，本文根据第1 节提出的磁环磁链计算模型得到磁环的ψ-I曲线，将其应用于非线性电感中得到磁环电磁暂态模型。为准确计算雷电流波的折反射过程及雷击过电压，输电杆塔模型采用无损多波阻抗模型，该模型利用输电杆塔的几何参数计算其塔身、横担和支架波阻抗，且支架波阻抗为塔身的9倍［22］。仿真中的杆塔为110 kV双回输电杆塔，参数见附录A表A3。

2.2 磁环材料的影响分析

为便于比较铁氧体、非晶及铁合金粉芯这3 种材料的雷击过电压防护效果，对3 种材料的磁环均进行以下设置：内、外半径分别为20、60 mm，长度为4 m，安装位置为避雷线上与第一基杆塔和第二基杆塔的连接处。遭受雷击后，不同磁环材料下第一基杆塔塔顶电压波形如图5所示，具体分析如下。

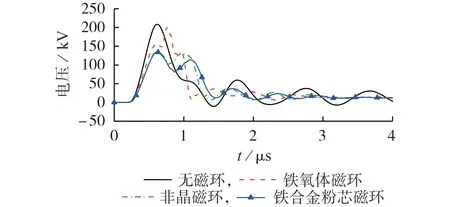
图5 不同磁环材料下第一基杆塔塔顶电压波形Fig.5 Voltage waveforms at top of first tower with different magnetic ring materials

1）与其他2 种材料的磁环相比，铁氧体磁环对第一基杆塔塔顶过电压的抑制效果较差，在0.615 μs 前，铁氧体的磁饱和效应较弱，表现为其第一峰峰值较无磁环的峰值208.63 kV降低了25.58%。但在0.67 μs 后，由于雷电流继续上升，铁氧体磁环工作在其ψ-I曲线的大电流区域，此时磁环基本饱和，抑制作用基本失效，电压数值继续上升，电压峰值较无磁环时只降低了3.64%，电压波前上升陡度由无磁环时的339.24 kV／μs下降为268.04 kV／μs。

2）非晶、铁合金粉芯磁环的电压峰值衰减幅度分别达到了34.48%、35.58%，波前上升陡度由无磁环时的339.24 kV／μs分别下降为222.26、218.52 kV／μs。这说明非晶与铁合金粉芯材料，尤其是后者对雷击过电压的抑制效果显著好于铁氧体材料，由此可见磁环材料的磁化曲线与饱和特性会显著影响磁环对雷击过电压的抑制效果。

由于铁合金粉芯材料的雷击过电压抑制效果在3 种材料中最优，下文研究其他因素对磁环的雷击过电压抑制效果的影响时，均采用铁合金粉芯磁环。

2.3 磁环截面积影响分析

将铁合金粉芯磁环的内半径、长度分别设置为20 mm、4 m，在30～80 mm 范围内改变磁环的外半径从而改变其截面积，则不同磁环截面积下第一基杆塔塔顶电压波形图如图6 所示。由图可见，磁环外半径越大，磁环对电压峰值的削弱效果越强，对后续波形振荡的消除效果越好，对雷击过电压的抑制效果越明显。

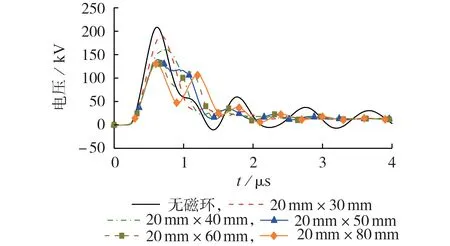
图6 不同磁环截面积下第一基杆塔塔顶电压波形Fig.6 Voltage waveforms at top of first tower with different magnetic ring cross sections

当磁环外半径由30 mm 变化至40 mm 和50 mm时，第一基杆塔塔顶电压迅速下降，峰值分别从无磁环时的208.63 kV 衰减为191.6、161.64、139.44 kV，抑制幅度分别达到8.16%、22.52%和33.16%，电压波前上升陡度较无磁环时的339.24 kV／μs 分别下降为277.7、229.28、221.33 kV／μs，陡度下降速率也较快。在60～80 mm 范围内继续增加磁环外半径，磁环的雷击过电压抑制效果会继续增强，但是已经明显出现饱和，当磁环外半径分别为60、80 mm时，第一基杆塔塔顶电压峰值分别衰减为134.39、130.64 kV，相比无磁环时分别下降了35.58 %、37.52%，电压波前上升陡度分别下降了218.52、211.97 kV／μs，与磁环外半径为50 mm 时相比，变化较微弱，这表明磁环外半径超过60 mm 后，磁环的雷击过电压抑制效果将逐渐出现饱和现象。

2.4 磁环长度的影响分析

将铁合金粉芯磁环的内、外半径分别设置为20、60 mm，在2～10 m 范围内改变磁环长度，仿真得到不同磁环长度下第一基杆塔塔顶电压波形图见附录A 图A3。由图可见，当磁环长度为2、4、6、8、10 m时，第一基杆塔塔顶电压峰值分别衰减为169.43、134.39、129.67、127.23、125.8 kV，较无磁环时分别降低了18.79%、35.58%、37.85%、39.02%、39.7%；电压波前上升陡度分别下降为242.04、218.52、212.57、211.35、209.67 kV／μs。由此可知，磁环长度对雷击过电压抑制效果的影响与磁环内半径类似，磁环长度越长，第一基杆塔塔顶电压峰值衰减越多，后续波形振荡越平缓，但磁环长度超过6 m 后磁环的雷击过电压抑制效果也逐渐饱和。

2.5 磁环形状的影响分析

在磁环实际应用时应考虑到使用相同体积的材料达到最佳的雷击过电压抑制效果，通过式（10）不难看出，相同体积下，不同形状的磁环ψ-I曲线一般不同，这将会影响磁环的雷击过电压抑制效果。以内半径为20 mm、外半径为40 mm、长度为4 m 的磁环的体积为基准，在30～80 mm范围内改变磁环外半径并计算对应的长度，仿真得到不同磁环形状下第一基杆塔塔顶电压波形图如附录A 图A4 所示。由图可见：在外半径80、60、50、40、30 mm 对应的5 种磁环形状下，第一基杆塔塔顶电压峰值分别衰减为201.7、192.19、180.27、161.64、142.55 kV，电压波前上升陡度分别下降为301.04、274.56、246.95、229.28、212.76 kV／μs；雷击过电压抑制效果最差的磁环形状为“内、外环半径分别为20、80 mm，长度为0.8 m”，对应的第一基杆塔塔顶电压峰值降低了3.32%，而效果最好的磁环形状为“内、外环半径分别为20、30 mm，长度为9.6 m”，对应的第一基杆塔塔顶电压峰值降低了31.67%。由此可见，当磁环的体积一定时，磁环的截面积越小，磁环越细长，磁环抑制塔顶雷击过电压的能力越强。

3 现场试验验证

3.1 试验现场布置

为验证本文所提磁环磁链计算模型及电磁暂态模型的正确性，开展110 kV 同塔双回输电线路现场试验，将仿真结果与试验结果进行对比验证。试验现场为广东电网公司接地技术与工程实验室，试验现场及其布置图如附录A 图A5 所示。试验现场有三基杆塔，塔高为27 m，第一基杆塔与第二基杆塔的档距为120 m，第二基杆塔与第三基杆塔的档距为30 m。接地装置与试验现场接地网相连，利用红相HX-4051 型雷电冲击电阻测试仪对现场杆塔的冲击接地电阻进行测量，测量示意图见附录A 图A6。取3 次测量的平均值，则三基杆塔的冲击接地电阻分别为1.61、1.56、1.54 Ω。

现场试验方式与第2 节类似，由冲击发生器产生幅值为20 kA 的8／20 μs 电流波并从第一基杆塔与第二基杆塔档距中央注入，测量第一基杆塔塔顶电压，试验时磁环装置采用多个磁环组成的磁环串的形式［21］，将之安装于避雷线上，因避雷线弧垂带来的重力水平分量及磁环串前的铜制卡扣使得磁环串能紧密贴合并固定在安装位置，并由高空施工人员确认磁环串中每个小磁环之间接触紧密无间隙。磁环串总长为4 m（由80 个内半径为10 mm、外半径为40 mm、长度为50 mm 的小磁环组成），安装磁环前后第一基杆塔塔顶电压波形的试验与仿真波形如图7 所示。

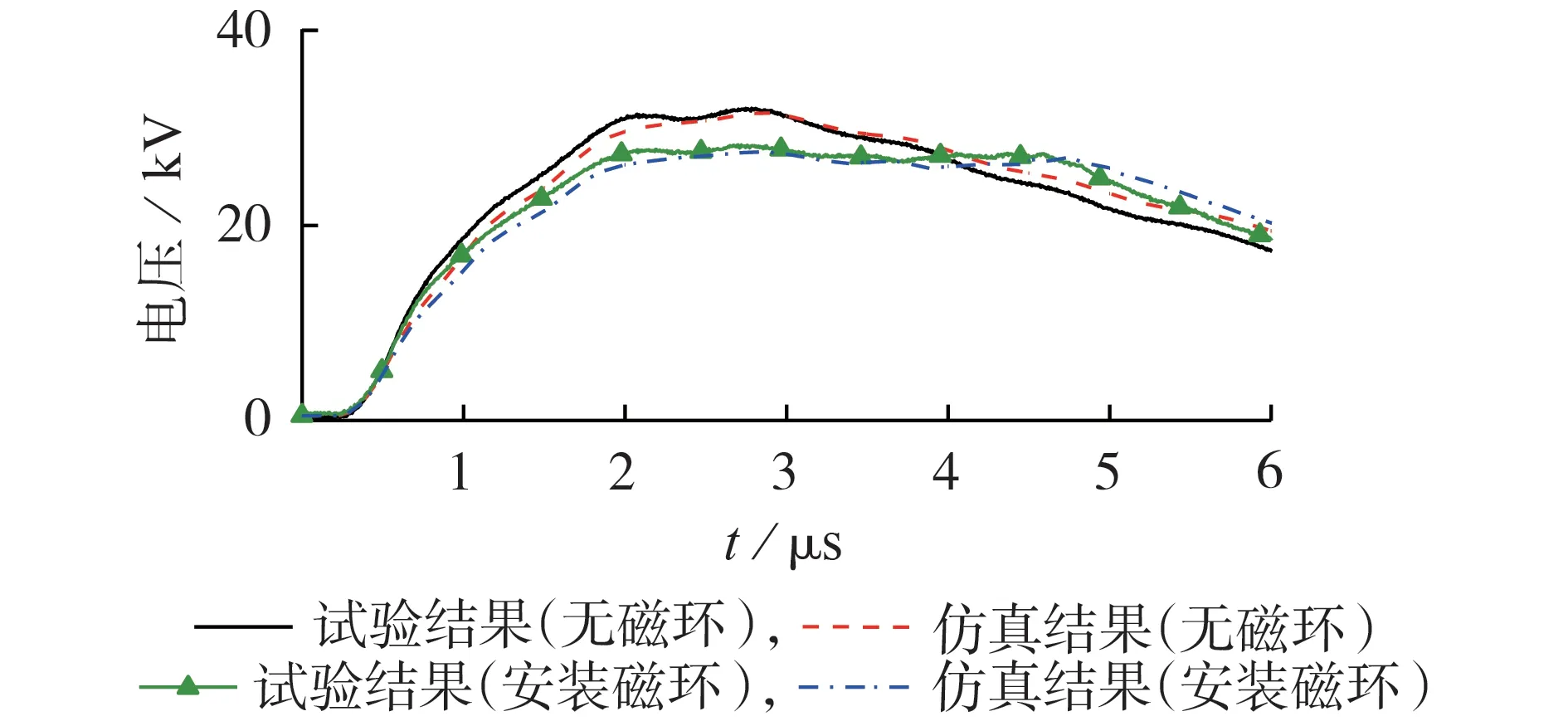
图7 安装磁环前后，第一基杆塔塔顶电压波形的试验与仿真结果Fig.7 Test and simulative results of voltage waveform at top of first tower with and without magnetic ring

3.2 试验结果分析

在无磁环时，试验与仿真的第一基杆塔塔顶电压峰值的试验、仿真结果分别为31.83、31.33 kV，电压波前上升陡度分别为11.35、10.96 kV／μs；安装磁环后，试验、仿真的电压峰值分别衰减为28.03、27.3 kV，比安装磁环前分别下降了11.94%、12.86%，电压波前陡度分别下降为10.31、9.7 kV／μs。安装磁环前后，仿真与试验结果的最大误差为5.92%，这充分证明了本文所提磁环磁链计算模型和电磁暂态模型的正确性以及磁环抑制输电线路雷击过电压方法的可行性。

此外，雷击避雷线中央时，雷击点过电压较大，磁环抑制作用会使其过电压进一步上升，空气间隙有击穿的风险，故本文针对该情况开展仿真研究，磁环参数设置与2.4节一致，雷击点波形图见附录A 图A7。由图可见，安装磁环后雷击点附近的电压的上升幅度较安装前的上升幅度小（最大上升幅度为6.92%），远不足以击穿避雷线与最近相线的空气间隙使得防雷失败。针对磁环抑制方法的雷击过电压防护效果，第2 节的仿真结果表明，磁环的雷击过电压抑制幅度最高可达39.7%，而文献［6］中接地电阻从30 Ω 降至15 Ω 后，塔顶电压下降了约43%，对比可知两者效果接近，但在实际改造中，降低接地电阻需要大幅增加杆塔接地装置尺寸或外引接地，工程量巨大，而磁环只需人工安装于杆塔避雷线附近即可，工程量小且实施简单，更适用于对已有输电线路的防雷改造。

4 结论

针对输电线路的雷击过电压防护，尤其是针对已有输电线路的防雷改造，本文提出利用磁环抑制雷击过电压的方法，主要结论如下。

1）根据材料的磁化函数能够较好地拟合铁氧体、非晶和铁合金粉芯磁环的磁化曲线，3 种材料的磁化函数拟合确定系数R2均高于0.999；3 种材料的磁环磁链计算模型与FEM 模型的计算结果之间的最大误差低于5%，验证了本文所提磁环磁链计算模型的合理性。

2）磁环材料的磁化曲线会大幅影响磁环的雷击过电压抑制效果，3 种材料中抗饱和性能更高的铁合金粉芯材料效果最佳；增加磁环截面积与长度能加强磁环的雷击过电压抑制效果，但随着参数增加会出现饱和现象，实际应用中磁环的外半径、长度分别取60 mm、6 m 时效果最佳；磁环形状也对磁环的雷击过电压抑制效果有一定影响，体积一定时，细长形状磁环的雷击过电压抑制能力更强。

3）根据110 kV 同塔双回输电线路的现场试验结果，安装磁环后第一基杆塔塔顶电压峰值下降了11.94%，这证明了磁环抑制输电线路雷击过电压的可行性；且仿真与试验结果的最大误差为5.92%，说明本文所提磁环磁链计算模型和电磁暂态模型较贴近实际情况。

附录见本刊网络版（http：//www.epae.cn）。