基于双层动态时段划分的配电网重构

2022-06-15傅长熠杨镜非顾家辉

电力自动化设备 2022年6期

傅长熠，杨镜非，顾家辉

（上海交通大学电子信息与电气工程学院，上海 200240）

0 引言

配电网重构是配电网优化运行中的一种重要技术手段，其通过对配电网线路中的分段开关和联络开关进行开合来改变网络的拓扑结构，从而改变配电网潮流分布，以实现降低网损、提高系统可靠性等目标。

配电网静态重构［1-2］仅考虑单一时间断面下的优化，而配电网动态重构则在此基础上考虑一个时间区间内参数的变化情况，在数学上是一个高维非线性不连续的组合优化问题，且求解过程中容易出现维数灾的问题，难以被直接求解。因此，如何对配电网动态重构问题进行简化和求解一直为研究的热点之一。文献［3］提出最优模糊C 均值聚类法进行时段划分，从而将所求解的问题转化为多个静态重构问题。文献［4］根据负荷情况进行聚类，以此实现时段的划分来求解动态重构问题。文献［5］通过引入区间数来处理分布式电源和电动汽车的不确定性，对各个时段进行静态重构后，再通过比较降损情况对各个时段进行合并。文献［6］通过负荷曲线的信息熵进行时段划分，并考虑了三相不平衡的情况。文献［7］采用微分进化算法以兼顾个体多样性与计算速度。文献［8］利用二阶锥松弛将配电网重构数学模型转化为凸规划进行求解，并通过仅让少数开关可以被操作来降低问题的复杂度。上述研究配电网动态重构问题的主要分析方法有2 类：一是将动态重构问题转化为多个静态重构问题，并利用提前划分好重构时段或是对静态重构后的相邻时段进行合并来实现动态重构，但利用该类方法划分得到的重构时段依赖于主观参数的选取，难以得到较好的优化结果，且无法处理如储能装置等涉及多个时段耦合的主动管理元素；二是通过建立数学模型来利用最优化方法进行计算，但动态重构问题的高复杂度使得研究学者必须对问题进行较大程度的简化才能在规定时间内完成求解。

配电网通常采用开环运行，因此考虑重构问题时需要建立辐射状约束的数学模型，由于其中通常包含大量整数变量，会较大地影响重构问题的计算效率。文献［9］提出了虚拟需求模型来表示辐射状约束，但需要引入大量辅助变量。文献［10］提出了生成树约束并被广泛运用，但该约束在某些场景下无法保证辐射状网络的生成。

基于此，本文提出了将割集法作为辐射状约束的表示方法。首先建立了双层优化模型，在利用二阶锥松弛处理非线性的潮流约束的基础上，通过分离出涉及时段间耦合的优化变量来提高问题的求解效率，从而实现重构时段的动态划分；然后结合数学优化方法与和声搜索算法对模型进行迭代求解；最后采用改进的IEEE 33 节点系统验证了所提动态重构方法的实用性和有效性。

1 配电网辐射状约束表示方法

1.1 常用辐射状约束表示方法

目前常用的辐射状约束表示方法包括生成树约束和虚拟潮流约束。生成树约束的思路为令除了变电站节点之外的节点都有一个父节点，其表达方式如下：

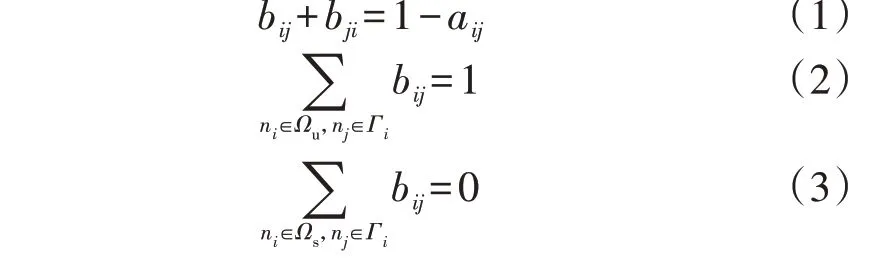
式中：aij为表示支路lij开断情况的0-1 变量，aij=0 表示支路闭合，aij=1表示支路断开；bij为表示节点ni与节点nj父子关系的辅助变量，bij=1 表示节点ni为节点nj的父节点，bij=0表示节点ni为节点nj的子节点；Ωs为变电站节点的集合；Ωu为非变电站节点的集合；Γi为与节点ni相连的节点集合。

虚拟潮流约束的思路为令除了变电站节点之外的每个节点都有大小为1 的虚拟需求，其表达方式如下：

式中：Λ为可能存在的支路lij构成的集合；vij为从节点ni流向节点nj的虚拟潮流的大小；N为网络中节点的数量；Ns为网络中变电站的数量。

上述常用的辐射状约束表示方法存在以下2 个问题：一是会引入大量的新变量与约束；二是约束中缺少体现各条支路间的联系的部分。上述2 个问题都会导致求解空间的增大，从而降低求解效率，且其中效率较高的生成树约束并不是生成辐射状配电网的充要条件［11］。基于此，本文提出新的辐射状约束表示方法。

1.2 基于解环法的辐射状约束表示方法

根据文献［12］，配电网辐射状约束可用如下2个条件进行描述：条件1，网络中闭合支路的数量为N-Ns；条件2，该网络为连通的网络。

各类处理辐射状约束的方法基本以上述2 个条件为基础，其中条件1 通常较易表示，而条件2 则较难表示。为了更好地用解析式来表达上述条件，本文用如下另外2 个条件对其进行替换：条件3，网络中的所有基本环路中都有一个开关被打开，各个基本环路中打开的开关相互独立，且同一开关不能被多个基本环路同时打开；条件4，网络中不存在孤岛，孤岛为不与变电站节点直接或间接相连的连通区域，将孤岛与网络主体相连的支路集合称为该孤岛所对应的割集。

条件3 作为十进制编码方式的基础，被广泛运用于各类采用启发式算法或智能算法求解配电网重构的问题中［13-14］。由此可知，满足条件3的网络必然满足条件1，且包含所有的可行解，此处不进行证明。由于连通的网络中必定不存在孤岛，不存在孤岛的网络必定连通，故条件4 为条件2 的等价条件。基于此，本文提出定理1：同时满足条件3 和条件4是网络满足辐射状约束的充要条件。

为了更好地利用数学模型表示条件4，将可能出现的孤岛分为如下2 类：第一类孤岛，不含有度大于等于3 的节点的孤岛；第二类孤岛，含有度大于等于3 的节点的孤岛。节点的度指该节点所连接的包含在基本回路中的支路数。2类孤岛的示意图如图1所示。

根据本文提出的定理1，可将配电网辐射状约束表示为：

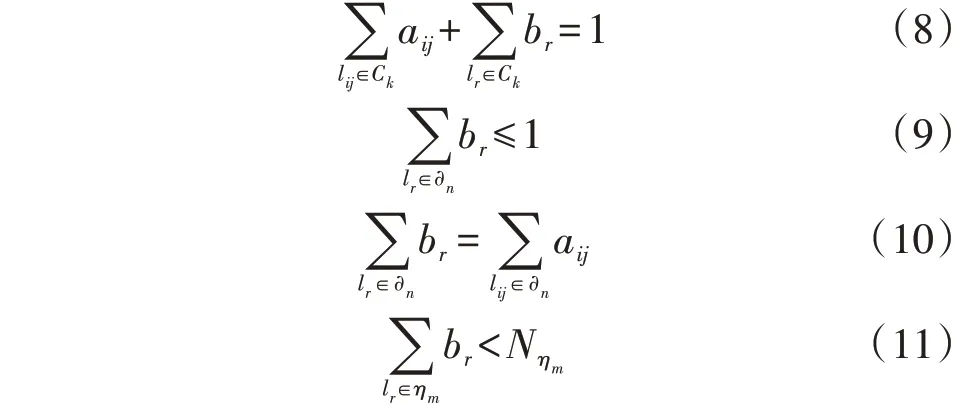
式中：Ck为第k个基本环路集合；∂n为不同基本环路间的公共支路集合，即∂n=Ck1∩Ck2；br为引入的辅助变量，每条公共支路中最多只能有1 个开关被打开，引入分属于不同基本回路的br来取代其中所包含的开关，使得不同基本回路中不存在共同的变量，从而使得条件3 能被满足，具体过程如图2 所示，并最终通过式（10）将br的状态转换回aij的状态；lr为转换后br所对应的支路；ηm为网络中第m个第二类孤岛对应的割集；Nηm为第二类孤岛对应的割集中边的数量。式（8）确保满足条件1；式（8）—（10）确保第一类孤岛对应的割集中的开关不被全部打开；式（11）确保第二类孤岛对应的割集中的开关不被全部打开，且采用辅助变量br以减少重复出现的情况。为方便后续说明，将本文方法称为割集法。

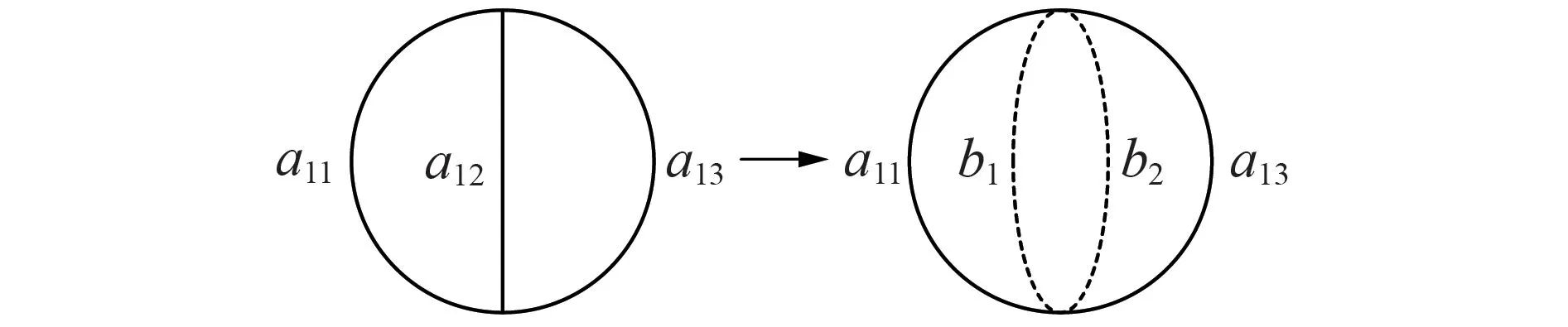
图2 辅助变量转化过程Fig.2 Transform process of auxiliary variable

将本文所提割集法与生成树法、虚拟需求法进行对比，相应的变量数、约束方程数如表1 所示［15］。表中：B为支路总数；K为基本环路数；M为第二类孤岛对应的割集数；P为公共支路数。考虑到配电网通常为弱环网，K、M、P远小于B、N，因此可以认为本文模型在大部分情况下相较于其他模型拥有更少的变量数与约束方程数。

表1 不同辐射状约束方法的对比Table 1 Comparison among different radial constraint methods

割集法中基本环路、公共支路、第二类孤岛对应的割集均需要通过事前的计算获取，这是本文模型相较于其他模型能有效减少变量数与约束方程数的原因。同时，这也使各个约束中均包含了大量线路状态间的信息，对于混合整数规划而言，该特点能有效削减搜索空间的大小。

2 配电网动态重构的二阶锥模型

2.1 约束条件

2.1.1 潮流约束

交流配电网常用的支路潮流模型为：

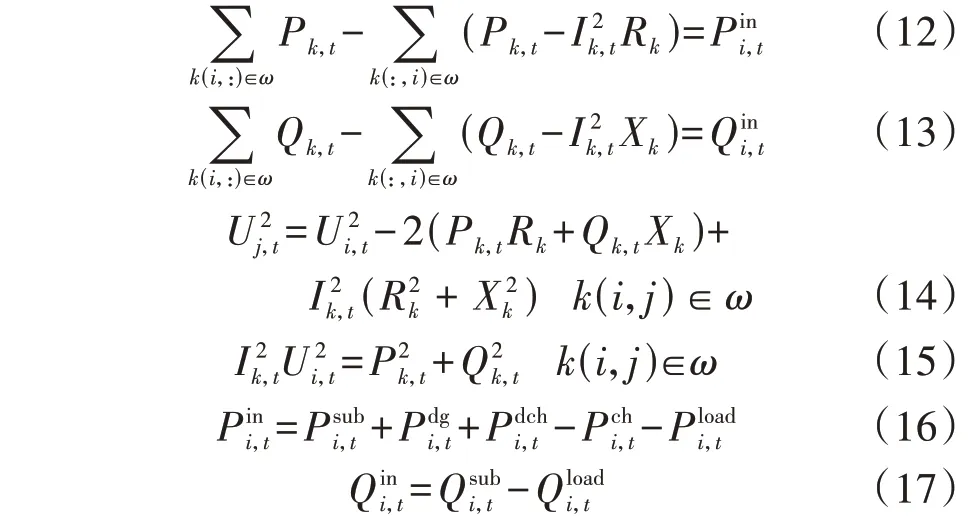
式中：下标t表示t时段；k(i，：)、k(：，i)分别表示首端为节点i和末端为节点i的支路k；ω为支路集合；Pk，t、Qk，t和Ik，t分别为支路k由首端节点流向末端节点的有功功率、无功功率和电流；Rk、Xk分别为支路k的电阻和电抗；Ui，t为节点i的电压；分别为节点i注入的有功功率和无功功率；分别为节点i处变电站的有功输出功率和无功输出功率；、分别为节点i处储能装置的放电功率和充电功率为节点i处分布式电源的有功输出功率；、分别为节点i的有功负荷和无功负荷。

2.1.2 潮流约束的二阶锥松弛

由于潮流方程为非线性方程，难以直接求解，因此通过引入中间变量对其进行转化。

用式（18）对式（12）—（15）中的相应变量进行替换，并对式（15）进行二阶锥松弛［16］。

式中：I͂k，t、U͂k，t为对应的辅助变量。

则潮流方程中的式（12）—（15）可以分别转化为式（19）—（22）。

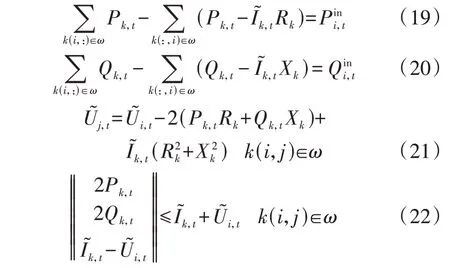
式（22）将对应的可行域松弛为整个二阶锥体内，成为凸可行域，使得问题能用商用求解器进行求解，且文献［16］通过分析与算例设置证明了松弛在不同目标函数下的准确性。

考虑到在配电网重构问题中，由于部分支路可能断开，式（21）不一定成立，利用大M法对其进行松弛，即：

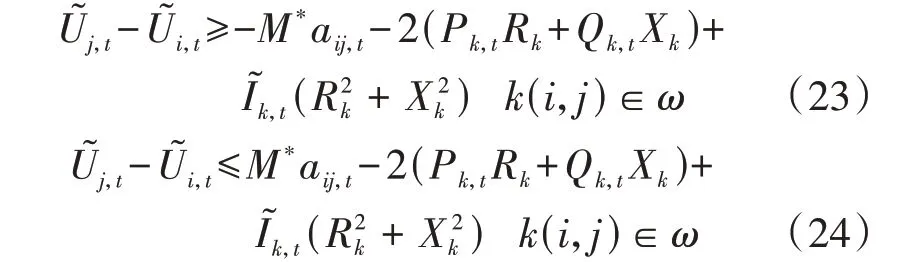
式中：M*为辅助变量，可取尽量大的正数。

松弛后的潮流方程由式（16）、（17）、（19）、（20）、（22）—（24）组成。

2.1.3 系统相关约束

此外，为保障系统的安全运行，配电网重构还需满足如下约束：

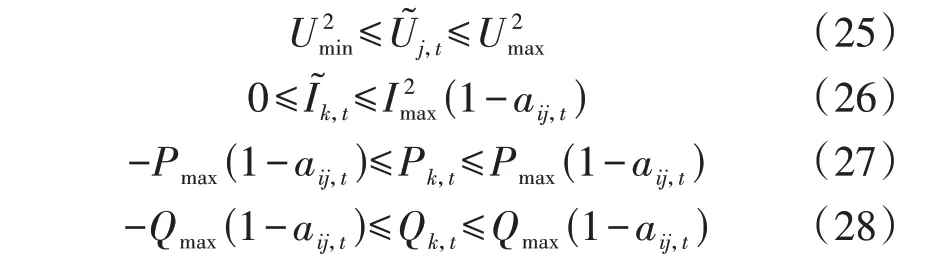
式中：Umin为电压最小值；Umax、Imax、Pmax、Qmax分别为电压、电流、有功功率、无功功率最大值。式（25）为节点电压约束，式（26）为支路电流约束，式（27）、（28）为支路功率约束。

由于配电网通常为开环运行，需满足辐射状约束式（1）—（4）。

2.1.4 主动管理元素建模

考虑分布式电源在一定情况下能通过弃风弃光参与主动管理，且仅考虑其有功出力，则其模型如式（29）所示。

2）储能装置建模。

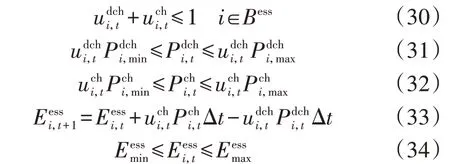
2.2 目标函数

本文模型以网损成本与弃风弃光惩罚费用之和C最小为目标函数，因此有：

式中：T为总时段数；Closs为网损价格；Cdg为弃风弃光的惩罚价格；ΩL为网络中可连通的支路集合；Ωdg为网络中安装分布式电源的节点集合。

3 双层优化模型

利用数学模型求解配电网动态重构问题时，理想状态下应将各时段下的每个开关状态都定义为变量。但这样会使得每增加一个时段，整数变量的数量都会大幅增加，从而导致计算时间呈指数级上升，在实际操作中不具备可行性。为解决这一问题，本文将第2 节所提模型转化为双层优化模型来进行求解。

双层优化模型以一个自然日为优化周期，以1 h为单位时间将其分为24 个时段。作为优化主体的上层优化将优化周期内经济性最优作为优化目标，将风、光、储能的出力状况作为决策变量；下层优化在上层优化确定出风、光、储能的出力状况的情况下，以网损最小为目标，确定进行重构的时段以及各个时段内的开关动作情况，再将各时段的拓扑结构返回至上层，以此进行迭代求解。

如果反射光线OB与x轴的正半轴所成的角为β(0°≤β<360°),如何确定镜面与水平面所成的角呢?(图4)

3.1 上层优化模型

由于开关操作将由下层优化传递而来，因而无需考虑辐射状网络约束与开关操作相关约束，上层优化模型为混合整数二阶锥规划模型。

因此，对于上层优化模型，其目标函数为式（35），需满足的约束条件为式（16）、（17）、（19）、（20）、（22）—（34）。

3.2 下层优化模型

下层优化以时段划分的结果和各时段内的开关开断情况为变量，以各时段网络的有功网损之和Cdown最小为优化目标。目标函数为：

下层优化中，时段划分的总次数Nc需满足如下最大重构次数约束：

式中：Nmax为最大重构次数。

除此之外，还需要满足的约束条件有式（8）—（11）、（16）、（17）、（19）、（20）、（22）—（28），即去除了主动管理元素的部分，并加入了开关操作约束与辐射状约束。

由于涉及各个重构时段间耦合的储能系统的相关变量由上层优化计算得到并传递而来，将其看作常数进行优化。因此下层优化中不涉及多个重构时段之间的耦合，故而可以得出以下结论：不同重构时段内的优化结果之间相互独立。进一步地，可以将考虑整个优化周期的优化模型拆分为不同重构时段下优化模型的组合，且单个重构时段内仅在最初时段进行开关的操作。在初始模型中，整数变量的数目为TB，搜索空间为2TB，而对其进行拆分后，转变为在Nc个问题中各自有B个整数变量，搜索空间变为Nc2B，相较于之前大幅减少。

对于拆分后得到的模型，利用和声搜索算法［17］确定重构时段的划分状况。和声搜索算法是一种智能优化算法，它模拟了音乐演奏的原理，有寻优速度快、过程简单的特点。各个重构时段内的开关状况则类似上层优化，同样为混合整数二阶锥规划模型，求解步骤如下：

1）设置初始参数，迭代次数k=1；

2）生成初始解；

3）将时段划分结果进行分类，分别求解各时段内的开关状态，对已计算过的时段采取简化策略，将未计算过的时段进行正常的优化计算，将重构结果返回并进行存储；

4）根据各时段内计算返回的结果计算适应度函数；

5）根据和声搜索算法进化策略进行迭代并生成子代种群，设k=k+1；

6）重复步骤3）—5）直至满足迭代终止条件；

7）输出计算结果，并且将参数传递至上层优化模型中。

具体的求解流程图见附录A图A1。

4 算例分析

4.1 算例参数说明

为了验证本文所提出的双层优化模型对于求解配电网动态重构问题的有效性，基于改进的IEEE 33 节点配电系统进行仿真。该配电系统含有5条联络线和32条普通线路，在此基础上，本文分别在节点16、19 处接入额定功率为1 000 kW 的光伏阵列PV1、PV2，在节点17接入额定功率为1000 kW的风机WT1，在节点15接入额定充放电功率为200 kW 的储能系统ESS1。网络结构图及基本环路情况如图3所示。

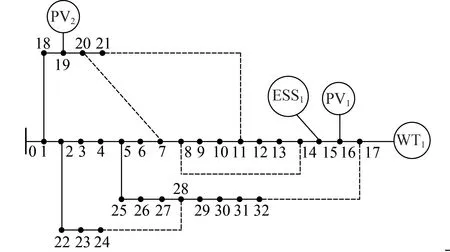
图3 改进的IEEE 33节点系统图Fig.3 Diagram of modified IEEE 33-bus system

以1 h 为一个时间单位，则一天可被分为24 个时段。将负荷分为居民负荷、商业负荷和工业负荷3 种，基础值为原算例值，3 种负荷在各个节点的比例系数、不同负荷的日变化曲线以及风电和光伏出力预测值的日变化曲线分别见附录A图A2—A4。

由MATLAB R2019b 编写算例程序，其中采用商用求解器的部分利用Yalmip 调用CPLEX 来进行求解。

4.2 算例仿真结果

对于本文所提出的辐射状约束表示方法，以IEEE 33 节点系统、IEEE 69 节点系统［18］、IEEE 123节点系统［19］为例，对比本文方法与生成树法、虚拟需求法在所需变量数以及约束方程数方面的差异，如表2所示。

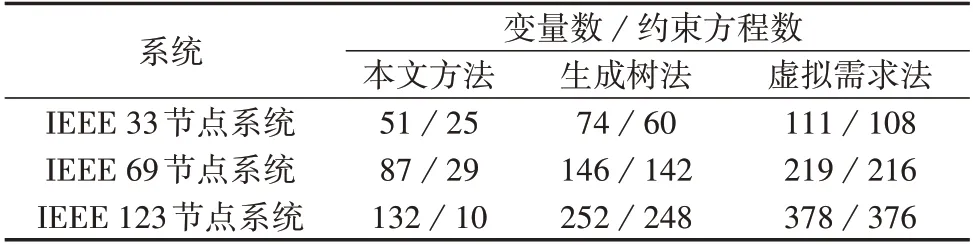
表2 不同辐射状约束方法的对比Table 2 Comparison among different radial constraint methods

由表2 可知，本文方法具有更少的变量数与约束方程数，且约束方程数与网络中节点和支路数量关联较小，更加适应常规配电网结构的特点，有助于提高求解配电网重构问题的计算效率。

此外，通过在IEEE 33 节点系统中进行1 000 次辐射状网络的随机生成，对不同辐射状约束表示方法进行测试，对比结果如表3所示。并结合第2节所建立的数学模型，将目标函数设为网损最小，应用于单时段静态重构中，进行1000次测试以观察其计算效率与优化结果，并与种群数量为30、迭代次数为30 的粒子群优化算法在静态重构问题中的优化结果进行对比，粒子群优化算法采用十进制编码方式对开关状态进行编码，对比结果如表4所示。

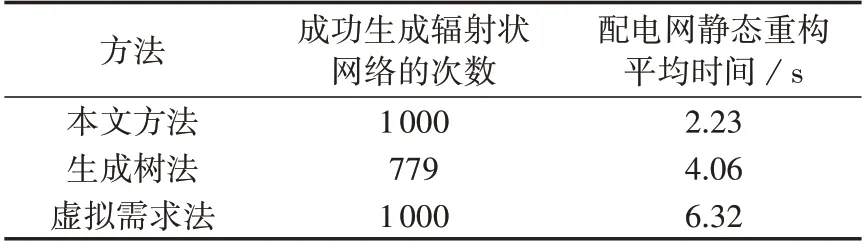
表3 不同辐射状约束方法计算效果的对比Table 3 Comparison of calculation effects among different radial constraint methods

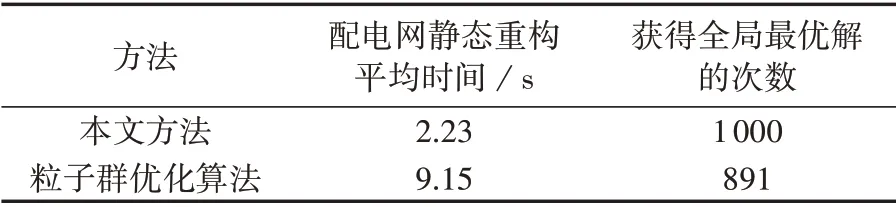
表4 不同配电网重构方法计算结果的对比Table 4 Comparison of calculation results between different distribution network reconfiguration methods

由表3 可知，本文方法与虚拟需求法均可确保生成辐射状网络，而根据第1 节可知生成树约束并非是生成辐射状配电网的充要条件。事实上，仅当网络中不存在分布式电源且无零负荷节点时生成树法才能确保生成的网络为辐射状网络。在计算时间方面，本文方法用时最少，且仅为虚拟需求法的35.3%，与3种方法中变量以及约束方程的数量关系相符合，证明了减少辐射状约束中的变量及约束方程数有助于提高重构问题的计算效率。

由表4 可知，采用二阶锥规划能稳定获得IEEE 33 节点系统下静态重构的全局最优解［20］，而粒子群优化算法由于其迭代过程中的随机因素较多，无法保证收敛至固定的结果，同时计算效率较低，证明了将二阶锥松弛应用于配电网重构问题中的可行性与优越性。

对于第3 节所建立的双层动态重构模型，设置最大重构时段数为4，储能装置的初始荷电状态与最终相同，取50%，储能电量上限为2 000 kW·h，Closs=200 元／（MW·h），Cdg=100 元／（MW·h）。和声搜索算法最大迭代次数为30，记忆库取值概率为0.7，微调概率为0.3。动态重构计算结果如表5 所示，表中列出了重构前、后各个时段开关的具体动作情况，并给出了对应的目标函数值。

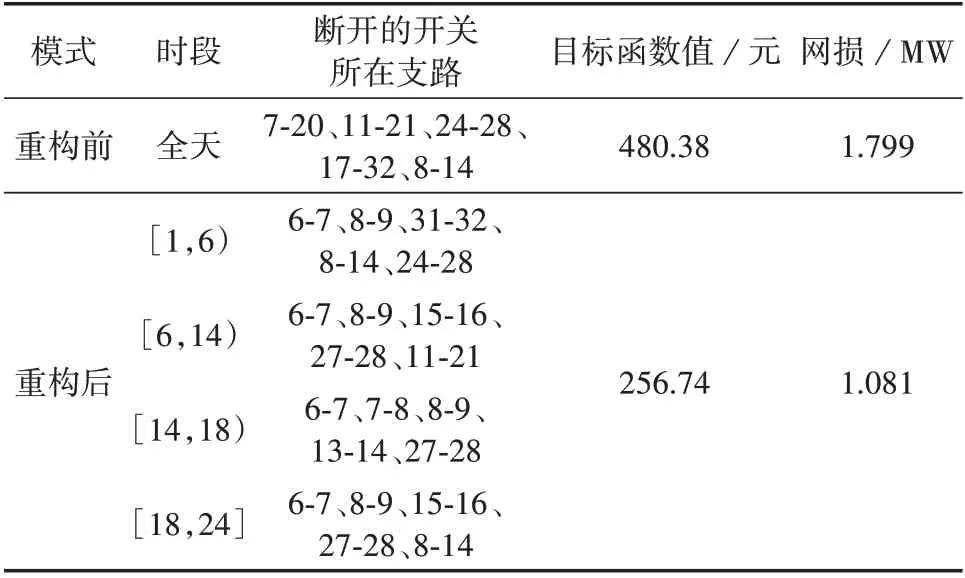
表5 动态重构计算结果Table 5 Calculation results of dynamic reconfiguration

由表5可知，重构后整个重构区间被划分为4个时段。可以看出，重构之后配电网通过多次对开关进行动作，有效地降低了网损及弃风弃光费用，改善了配电网的运行状况，说明了本文方法能有效求解配电网动态重构问题，提高配电网运行的经济性。同时，本文方法在迭代4 次后收敛，体现了良好的收敛性。

图4 为分布式电源的弃风弃光功率和储能装置的充放电功率曲线。可以看出，在凌晨时段，弃风弃光情况较为明显，原因在于此时负荷较小，且储能装置有最大充电功率的限制，无法消纳剩余的清洁能源。储能装置在负荷低谷期与分布式电源出力的高峰期进行充电，在负荷高峰期进行放电，有效实现了削峰填谷的功能。此外，采用本文提出的基于双层动态时段划分的配电网重构方法后，弃风弃光的情况明显减少，证明了采用该模型对主动管理元素的优化有明显效果。

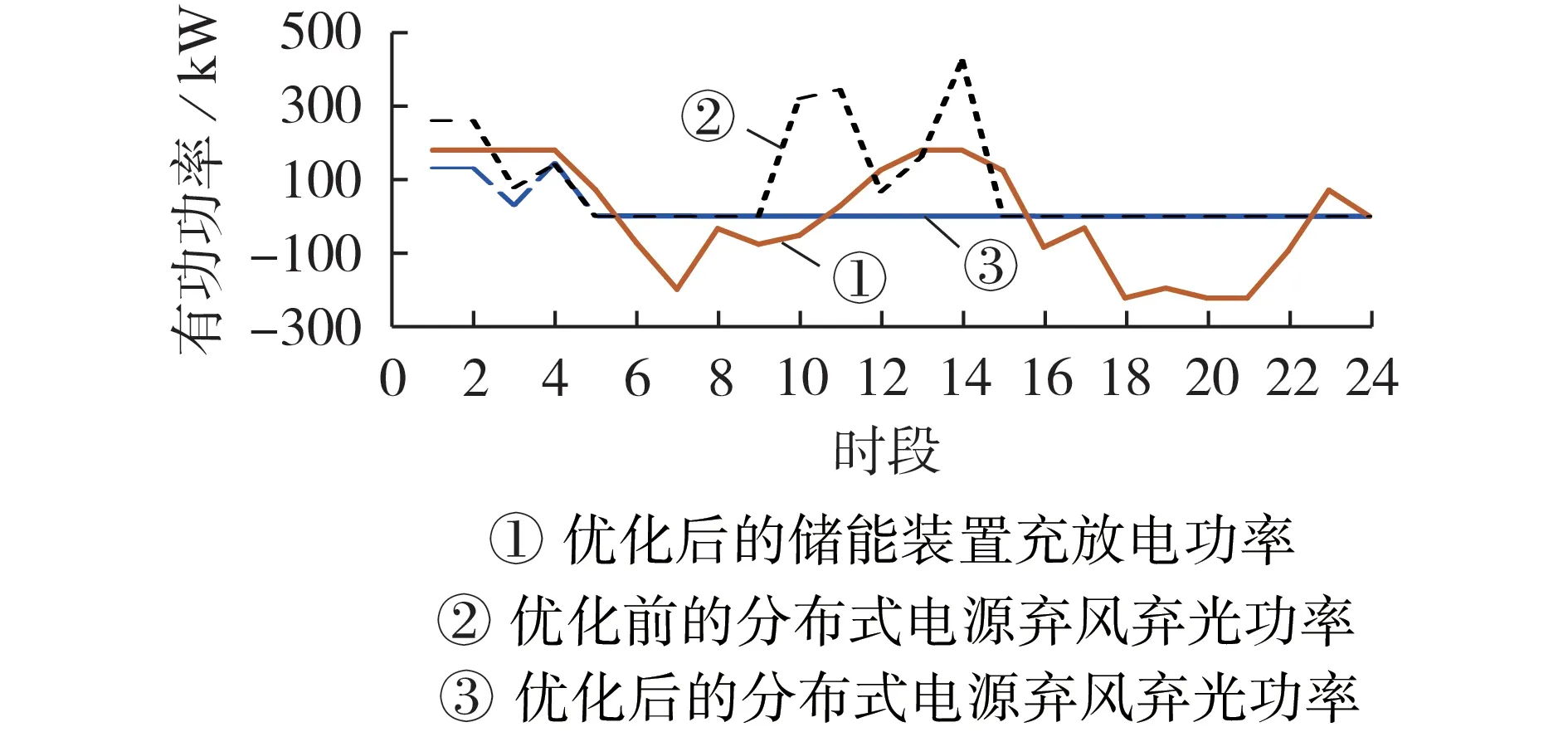
图4 分布式电源弃风弃光功率与储能装置充放电功率曲线Fig.4 Curves of abandoned wind and photovoltaic power of distributed generation and charging and discharging power of energy storage device

此外，为了验证本文所提出的双层优化方法的合理性与优越性，在控制相关参数不变的情况下，选取了如下3 种方法进行对比：文献［3］采用的C 均值聚类法，根据各个时段的负荷情况利用聚类进行时段划分，再进行静态重构；文献［5］使用的合并时段法，先对各时段进行静态重构，再进行时段的合并来生成最终的结果；不采用第3 节所提出的方法，直接利用单层模型进行求解。本文方法与上述3 种方法的仿真结果对比如表6所示。

表6 不同动态重构方法结果对比Table 6 Comparison of results among different dynamic reconfiguration methods

由表6 可知，直接采取单层优化的方法在运行24 h 之后仍无法得到结果。结合表5 可以看出，除了在测试时间内无法完成求解的单层优化方法之外，其他3 种方法相较于未重构，均能有效降低系统的经济成本。其中本文方法下的目标函数值最低，优化结果最佳，C 均值聚类法次之，合并时段法效果最差。这是由于C 均值聚类法只考虑了各个时段负荷水平的相似性，但并未考虑负荷水平相似的时段是否适合采用相同的静态重构结果，而合并时段法只能作用于相邻时段，与其他2 种方法相比缺少对全局情况的考虑。同时，C 均值聚类法和合并时段法也难以处理储能装置这类涉及多时段间耦合的主动管理元素，导致优化效果不佳。对于采取单层优化进行求解的策略，虽然其在理论上能够成功进行求解，但是在实际测试中由于问题复杂度过高而无法在限定时间内完成求解；而本文提出的考虑时段动态划分的双层优化方法则是充分考虑了各类变量之间的关联，在不对问题进行大幅度简化的前提下，大幅提高了优化效率，有效解决了配电网动态重构问题。