基于改进经验小波变换和改进多视角深度矩阵分解的直流配电网故障检测方案
2022-06-15连淑婷郭谋发
洪 翠,连淑婷,黄 晟,郭谋发
(1. 福州大学 电气工程与自动化学院,福建 福州 350108;2. 福州大学 计算机与大数据学院,福建 福州 350108)
0 引言
随着新能源与电力电子技术的快速发展,分布式电源并网需求增大,直流负荷比重不断增加。传统交流配电网需通过电力电子换流装置实现分布式电源的消纳以及直流负荷的供电,采用直流配电网不仅可向各类直流负荷直接供电,省去分布式电源和储能装置并网时的电力电子转换装置,并且直流配电网具有传输效率高、电能质量好、供电可靠性高等优势[1]。然而,保护技术的不成熟在一定程度上限制了直流配电网的大范围应用。与交流配电网相比,直流配电网的系统阻抗低[2],故障电流上升速度快且幅值高,将对换流站中的二极管带来冲击,进而可能危害直流配电设备[3]。为保护直流配电网中的电力电子器件,需尽快实现故障隔离。快速可靠的故障检测将为保护动作奠定良好的基础,是直流配电网保护方案不可或缺的关键环节。
近年来,国内外学者已对直流配电网故障检测开展了深入的研究。文献[4]提出以换流站直流侧电流、电压作为故障检测的判据,当电流超过设置的阈值且直流电压下降到一定程度时判定为故障,但容易出现误检、漏检。文献[5]利用故障后电流反向增大过零的特性,通过采样数据前后异号判断电流是否过零,从而检测故障,在雷击干扰情况下不会误动,可靠性较高,但高阻接地情况下是否能正常检测有待商榷。文献[6]提出名为“握手法”的故障线路识别方法,其假定电流正方向为母线流向线路,当正方向过流时判定为发生故障,该方法简单易行,但识别速度难以达到速动性要求,且非故障线路会短时停电。文献[7]提出基于暂态电流均值的直流故障检测方法,将电流在一个固定时间窗内的均值作为故障检测判据,速动性好。文献[8]将直流电抗器作为边界,以其两端电压构造检测判据,该方法无需数据同步,但直流电抗器不可或缺。为提高直流配电网故障检测的可靠性,已有学者将信号处理算法应用于故障数据预处理。文献[9]选择短时傅里叶变换STFT(Short-Time Fourier Transform)处理故障电流信号,以频谱中的幅值作为故障检测判据,能在几毫秒内检测出故障,但是STFT 存在窗函数选择问题[10]。文献[11]利用换流器开关带来的线路6 次谐波分量,提出一种基于改进的离散傅里叶变换IDFT(Improved Discrete Fourier Transform)的故障定位方案,该方案可消除衰减周期分量和直流分量的影响,准确性好。文献[12]采用改进互补集合经验模态分解CEEMDAN(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise)算法自适应地提取暂态零模电流的特征模态分量,构造能量比判据,以此区分高阻接地故障、负荷投切等工况,灵敏度高。
随着人工智能技术的发展,机器学习算法逐渐开始应用于直流故障检测领域。文献[13]基于归一化故障电流生成并训练深层神经网络DNN(Deep Neural Network),完成了直流配电网故障特征的学习和提取。文献[14]采用STFT 对船舰直流配电系统故障电流进行预处理,然后将其输入K-means 聚类算法中进行故障检测及识别,避免了硬判据对故障检测造成的影响。文献[15]提出基于经验模态分解EMD(Empirical Mode Decomposition)和卷积神经网络CNN(Convolutional Neural Network)的直流输电系统故障检测方案,将EMD 得到的特征量输入离线训练好的CNN 中进行故障检测。但总体而言,人工智能算法在直流配电网故障检测领域的应用较少。
为了克服以单一电气量进行故障检测时容易出现误检、漏检的问题,同时满足故障检测速动性的要求,本文提出一种基于改进经验小波变换IEWT(Improved Empirical Wavelet Transform)和改进多视角深度矩阵分解IMDMF(Improved Multi-view Deep Matrix Factorization)模型的直流配电系统故障检测方案。通过修改经验小波变换(EWT)中经验小波函数的相频响应,使之尽可能与局部信号的相频特性相匹配;在多视角深度矩阵分解(MDMF)模型前端设计了权重自学习网络,依据多视角数据对分类任务的重要性分配不同的权重,从而提高故障分类识别的精度。与现有利用信号处理算法的故障检测方案相比,IEWT对故障频带上的信号成分提取能力更强,使得故障检测方案可靠性进一步提升。此外,本文所提故障检测方案可实现交流侧故障的识别,提高了方案的完备性,且在出现误判的极端情况下,IMDMF 模型也可将其单独划分出来,防止保护误动。基于PSCAD/EMTDC 仿真平台搭建了直流配电系统模型,仿真结果验证了本文方案的可行性。
1 直流配电网故障分析
手拉手式柔性直流配电系统拓扑结构及其时域故障分析详见附录A。为更全面地了解线路发生故障后电流的变化,利用离散傅里叶变换进行频域分析。金属性单极接地故障与正常运行时的电流幅频谱如图1 所示,金属性单极接地故障电流的相频谱如图2 所示。图中:Iamp为电流幅值;φI为电流相位。
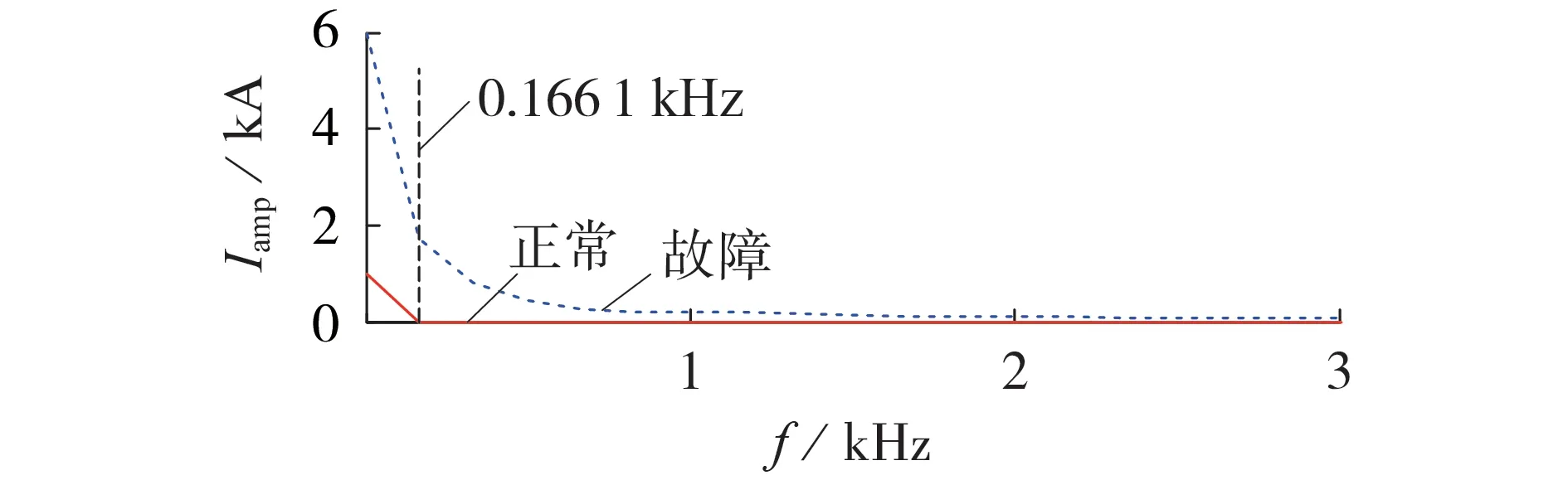
图1 金属性单极接地故障与正常运行时的电流幅频谱Fig.1 Amplitude-frequency spectrum of current under metallic single-pole grounding fault and normal operation condition
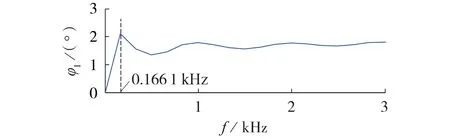
图2 金属性单极接地故障电流相频谱Fig.2 Phase-frequency spectrum of metallic single-pole grounding fault current
由图1 可见,金属性单极接地故障频带大致集中在第1个转折点之后的区段上。由图2可见,在第1 个转折点之后,故障电流相频谱由线性上升转变为非线性波动,即等效故障电流的正余弦波相位发生了改变。
同理可得极间短路故障电流的幅频谱、相频谱如图3所示。
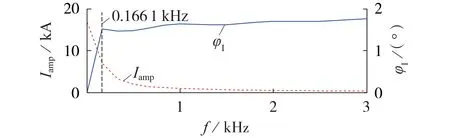
图3 极间短路故障电流的幅频谱、相频谱Fig.3 Amplitude-frequency and phase-frequency spectra of inter-pole short circuit fault current
由图3 可见:极间短路故障与金属性单极接地故障频带一致,集中在第1 个转折点之后的区段,但等效故障电流的正余弦波幅值较大,主要原因是该幅值大小与故障电流幅值密切相关,而极间短路故障回路不包含电容接地电阻Rg,得到的故障电流幅值更高,由离散傅里叶变换得到的等效故障电流幅值也更高;同时,极间短路故障电流的相频谱波动程度较低。
附录A 图A1 中f3处在2 s 发生单相接地、两相接地、三相短路故障时,换流器2 直流出口线路(下文统称为观测线路)的正极电流ip如附录B 图B1 所示。由图可见,交流侧发生不对称故障时,故障点将通过换流站与直流配电区域之间形成零序环流通路,直流线路在该零序环流作用下将产生交流基频波动,直至故障消失。为进一步验证该理论,对图B1 所示的正极电流进行离散傅里叶变换,得到正极电流幅频谱,如附录B 图B2 所示。可见,交流侧发生不对称故障时,观测线路上的电流确实存在50 Hz 的交流电流分量,而故障电流的相频谱在前段频带上差异较大。当系统交流侧发生三相短路故障时,故障电流的特征与发生极间短路故障时类似。
综上所述,频域范围内,故障频带上的信号量与正常工况相比差异明显,若能将该频带上的信号成分尽可能地分解出来,则更有益于故障检测。
2 算法理论
2.1 IEWT
EWT 是由Gilles 提出的一种信号处理方法[16],它将EMD 的自适应原理和小波变换(WT)的理论框架相结合,能自适应地分解信号。分解步骤为:①利用傅里叶变换获得信号的频谱,通过寻找频谱内极大值的方式将频谱划分为M个区域;②根据频带划分结果定义经验小波尺度函数、经验小波函数;③利用传统小波框架计算经验小波系数c1—cM;④采用经验小波尺度函数、经验小波函数及经验小波系数重构信号。
由第1 节的分析可知,直流线路发生故障后,线路电流的相频谱发生突变,从线性上升变为非线性波动,因此,考虑改变经验小波的相频特性,使之尽可能地与局部故障信号的相频响应相匹配,从而获得能量更集中的分解系数,更多地捕获故障信号的能量,但多分辨率分析MRA(Multi-Resolution Anal‐ysis)空间结构应在改造前后保持不变。文献[17]提出,对Meyer 小波增加满足式(1)所示特定条件的非线性相位函数θ( )ω时,可得到具有相同空间结构的正交小波基。
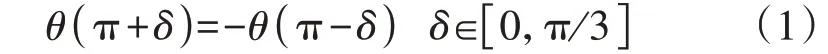
Meyer 小波定义域为频域且满足一定框架,而EWT 所定义的小波满足Meyer 小波形式,即亦满足上述理论的前提条件。
故障电流信号f(t)经过傅里叶变换后可表示为(ω)=r(ω) ejξ(ω),其中r(ω)为̂(ω)的绝对值,ξ(ω)为故障电流信号的相位函数。IEWT的经验小波函数ψ(t)经傅里叶变换后可表示为(ω)=̂(ω) ejθ(ω),其中̂(ω)为经傅里叶变换后的EWT的经验小波函数,θ(ω)在满足式(1)的条件下与ξ(ω)越相近,则分解系数的能量越集中。
考虑到在线拟合函数θ(ω)可能导致故障检测程序耗时较长,因此,本文采用类似查表的方式,即先离线拟合不同故障信号相频谱的离散序列,获得函数θ(ω),然后在线选取θ(ω)代入经验小波函数(ω)中。其中,拟合方式采用最小二乘法非线性拟合,拟合区段为信号相频谱的第1个转折点之后。
以正极金属性接地故障(Rg=0)为例,不同故障距离下故障信号的θ(ω)如表1所示。
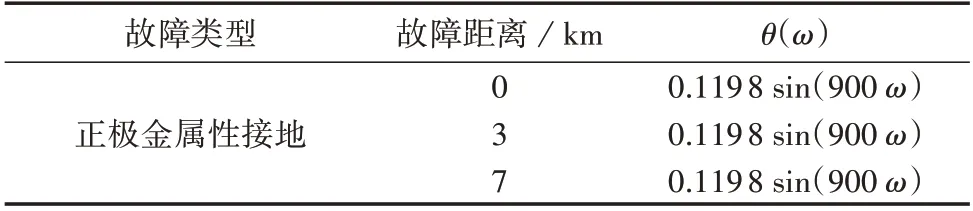
表1 不同故障距离下故障信号的θ(ω)Table 1 θ(ω)of fault signals under different fault distances
由表1 可见,故障距离发生变化时,线路等效电阻、等效电感值变化不大,并不影响拟合的θ(ω)。然而在实际运行中,直流配电网发生故障时的过渡电阻、故障位置均未知,无法根据过渡电阻数值在线选择合适的θ( )ω。因此,本文采用电流变化率作为函数θ( )
ω在线选择的依据,不同故障信号的电流变化率di/dt如表2所示。
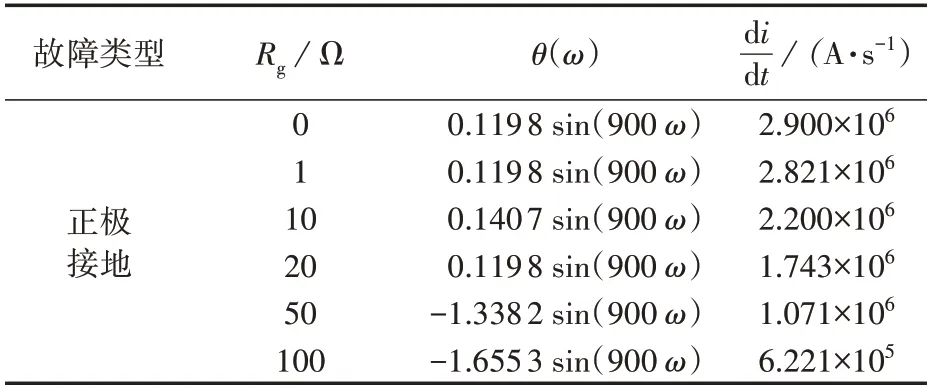
表2 不同故障信号的θ(ω)与di/dtTable 2 θ(ω)and di/dt of different fault signals
实际应用中,故障发生时的环境并不完全一致,无法将di/dt确定为一个具体值,因此,将仿真获得的电流变化率数值在一定范围内进行扩大。表2 中,过渡电阻为10 Ω 的正极接地故障对应的θ(ω)=0.1407 sin(900ω),相比其他情况下的θ(ω)较为独特,因此分别取θ(ω)为0、0.119 8 sin(900ω)、0.140 7 sin(900ω),并将其代入经验小波函数,经IEWT分解得到的细节分量c3如图4所示。
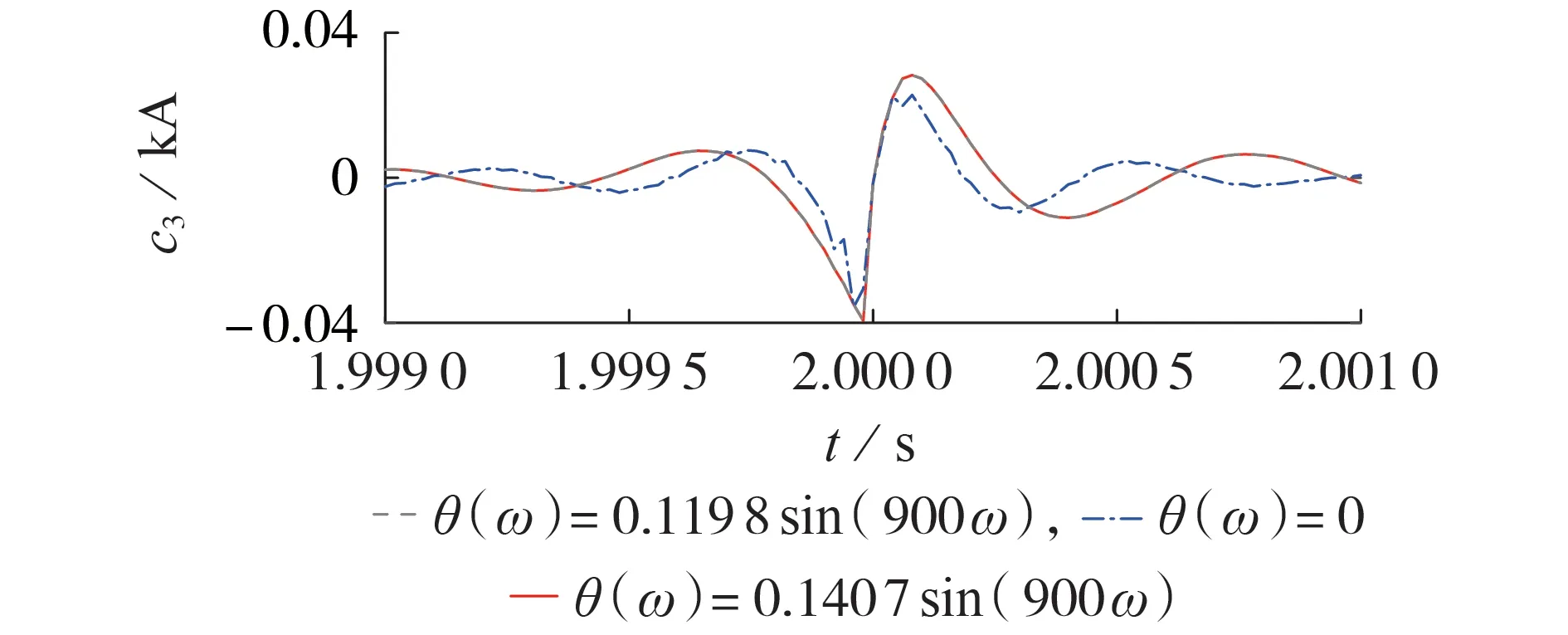
图4 不同θ(ω)对应的c3Fig.4 c3 responding to different θ(ω)functions
由图4 可以看出,即使电流变化率上浮20%,在线选取θ(ω)=0.119 8 sin(900ω)所得结果与选取θ(ω)=0.1407 sin(900ω)时相差无几,这表明该范围的选取较为宽松。
综上所述,IEWT可根据故障现况选择合适的函数θ(ω),使经验小波函数与故障电流信号的相频特性匹配度较高。以正极金属性接地故障为例,改进后的经验小波函数为:
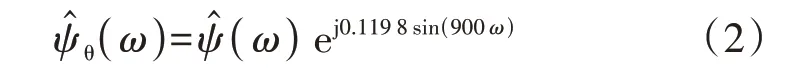
图A1中f2处发生正极金属接地故障时,故障电流及其IEWT和EWT结果如图5所示。
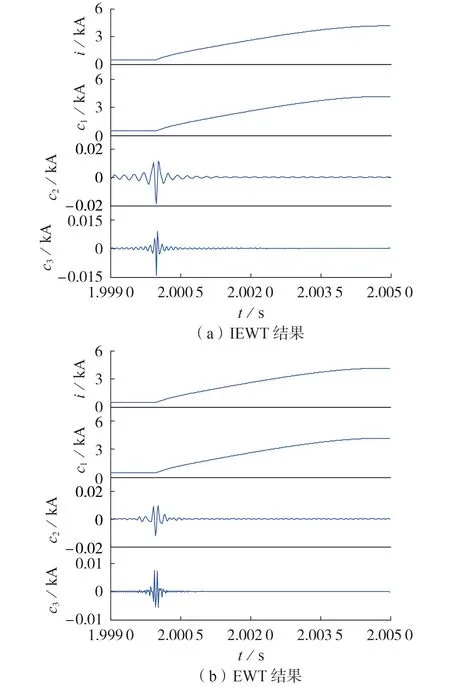
图5 f2 处发生正极金属接地故障时的故障电流及其IEWT、EWT结果Fig.5 Fault current and its IEWT and EWT results when metallic positive-pole grounding fault occurs at f2
对比图5(a)、(b)可见,由IEWT 分解得到的细节分量c2、c3中的最大系数绝对值要比由EWT 得到的大,即IEWT 捕获到的故障信号的能量更多,更有利于区分故障状态与正常状态。其中:近似分量c1仅展现了信号的概貌,难以表征电流的奇异点;细节分量c2、c3可准确反映故障特征,但与c2层相比,c3层的系数能量更集中,特征更显著。因此,本文选择c3层构造故障检测判据。
由图5(a)可见,调整经验小波函数的相频响应后会带来纹波,可能导致重构信号的失真。但是,故障检测领域中可以适当考虑牺牲少量重构还原度而获得较大的系数能量。分别利用IEWT和EWT重构图A1中f2处的正极金属性接地故障电流,结果如附录B 图B3 所示。图中:IEWT 重构信号整体上与原始信号一致,其均方误差为5.25×10-6kA;EWT 重构均方误差为1.17×10-8kA。由此可知,IEWT 能在重构信号不严重失真的情况下使分解出的能量更加集中,且局部表征故障的能力更强。
2.2 MDMF及其改进
模式识别问题中,特征提取算法是最为关键的一环。矩阵分解是一种有效的特征提取方式,但传统的矩阵分解只是对数据的单次解读,无法实现较好的表征能力。因此,可将矩阵分解拓展到多级的情况,即深度矩阵分解。深度模型可以自动学习每一层的潜在属性,使得在最内层的表示矩阵具有最强的表征能力。一般而言,故障时刻的电流信号具有多种特征,能更好地从不同角度揭示故障的本质。
MDMF可以表示为:
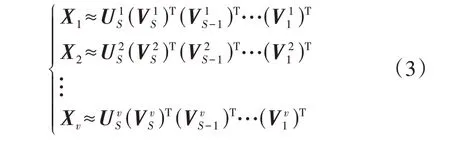
式中:v为视角个数;S为深度分解的层数;X1—Xv分别为第1—v个视角的数据矩阵;U—U分别为第1—v个视角的表示矩阵;(V)T—(V)T分别为第1—v个视角的基矩阵。
由式(3)可知,MDMF 对多视角数据X1—Xv进行独立处理,获得对应的表示矩阵,这将使整个矩阵分解模型较为庞大、参数较多,且模型运行时间较长。若将多视角数据进行融合,得到多视角数据共有的表示矩阵,则可简化MDMF 模型,缩短运行时间。但通过拼接简单地将多个视角的特征组合在一起,不仅会带来大量的冗余信息,还可能丢失特征数据之间的关联信息。因此,本文在MDMF 模型前端添加权重自学习网络,通过权重学习使得对分类任务具有较大作用的数据在MDMF 中占有较大的权重,即数据点对应的权重与其在分类任务中的重要性成正比。该网络可表示为:
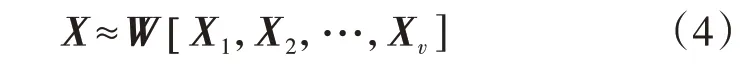
式中:[X1,X2,…,Xv]为将数据矩阵进行横向拼接后得到的矩阵;W为权重自学习网络中的权重矩阵。
W采用表示统一化策略,使得MDMF 符合现实意义,即多视角数据为波形在不同空间的映射,则IMDMF模型可描述为:
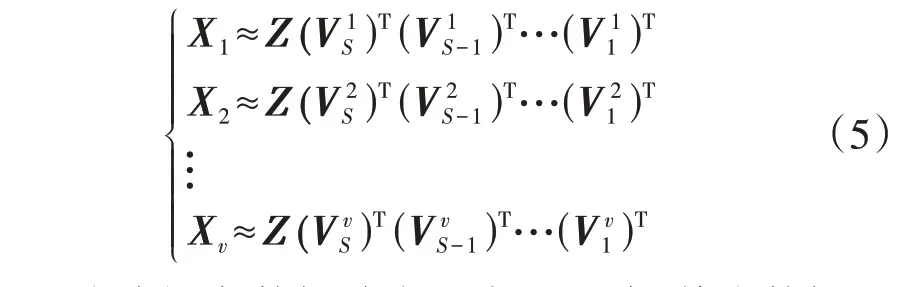
式中:Z为多视角数据共有的表示矩阵,其为数据矩阵与表示矩阵的乘积,其实际意义是各个数据点在底层的真实表征。
选取S=4,将IEWT 得到的c1—c3和线路极间电压udc作为输入多视角数据,则本文提出的IMDMF模型如图6 所示。图中:①—④分别表示权重学习模块、编码器模块、多视角数据表示模块、各视角的解码器模块;权重自学习网络中不同的灰度即代表不同的数据权重。
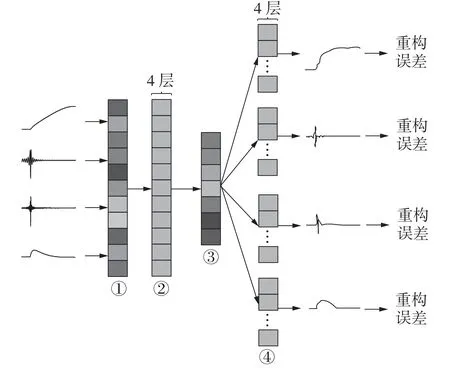
图6 IMDMF模型Fig.6 Model of IMDMF
考虑到IMDMF 模型提取的Z已具备较强的故障表征能力,因此放弃其他具有特征提取模块的分类器,直接采用软分配层实现故障类型的识别,从而进一步简化分类模型。软分配层可将Z以不同的权重分配给不同的类别,如式(6)所示。

式中:Wc为类别分配权重矩阵;G为类别得分矩阵。分类的误差函数使用交叉熵,数学表达式为:
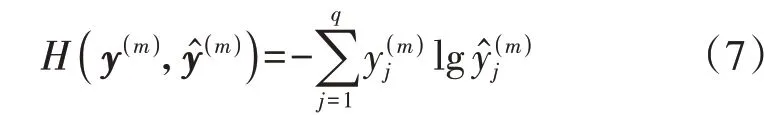
为直观反映各个类别的概率分布情况,进一步将式(6)获取的类别得分矩阵通过Softmax 函数映射至0~1 范围内,且所有类别概率之和为1。Softmax函数表达式为:
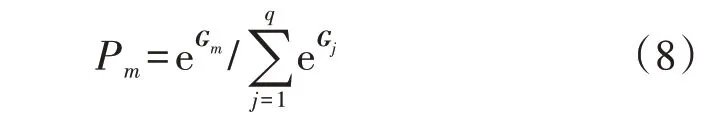
式中:Pm为类别m的概率;Gm、Gj分别为类别m、类别j的等分矩阵。
3 故障检测方案流程
本文所提基于IEWT和IMDMF的直流配电网故障检测方案的流程如图7所示。
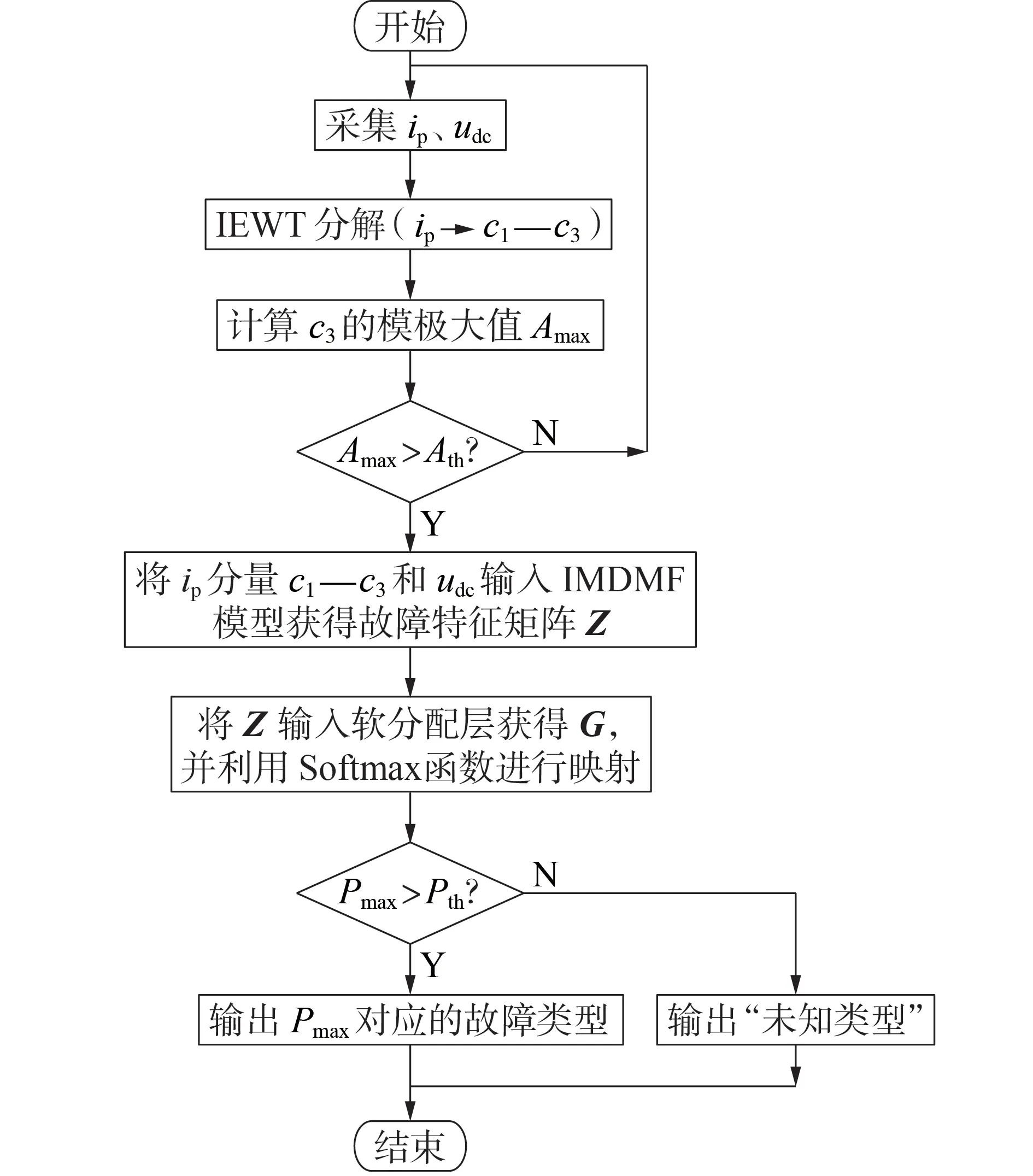
图7 本文所提故障检测方案的流程Fig.7 Flowchart of proposed fault detection scheme
选取c3的模极大值Amax作为故障检测判据,以避免IEWT 在突变点附近的纹波对故障检测带来的影响,故障检测判据为:

式中:Ath为阈值,按照躲过负荷扰动的基本原则进行选取。
由式(8)可知,Softmax 函数的输出是各个类别的概率,故设定阈值Pth,以确定最终的预测类别。取最高概率值Pmax及其对应的类别,若Pmax满足式(10),则输出对应类别;否则,输出“未知类型”。

4 方案验证
4.1 仿真建模
在PSCAD/EMTDC 仿真平台上搭建图A1 所示的手拉手式柔性直流配电系统仿真模型。其中:电压源型换流器VSC1采用定直流电压控制模式,VSC2采用定有功功率控制模式;电压源型换流器直流侧采用电容中性点经5 Ω 电阻接地方式;柔性直流配电系统负载为交流微电网、交流负荷、直流微电网、直流负荷4 类;直流线路采用RL 等效模型,主要的仿真模型参数见附录B表B1。
4.2 故障检测仿真
4.2.1 不同故障场景下的检测性能
依照如图7 所示的工作流程,仿真验证本文提出的故障检测方案的性能。以图A1 中观测线路上保护装置为例,采样频率为50 kHz,数据窗的长度为100 点。负荷投切时,由IEWT 得到的c3模极大值Amax=8.4×10-5kA,考虑裕量,将其乘以可靠系数5,最终设定c3的模极大值阈值为Ath=4.2×10-4kA。不同故障场景下,本文所提故障检测方案的结果如表3所示。表中:观测线路近端、远端故障的距离分别设定为0、7 km;观测线路背端即VSC2交流侧。
由表3 可见,本文所提方案在不同故障场景下均能可靠检测出故障。但故障距离的增加会导致线路等效电感及电阻值变大,由附录A可知,故障电流的幅值变小,相应地,由IEWT得到的c3幅值减小,模极大值Amax也随之减小。
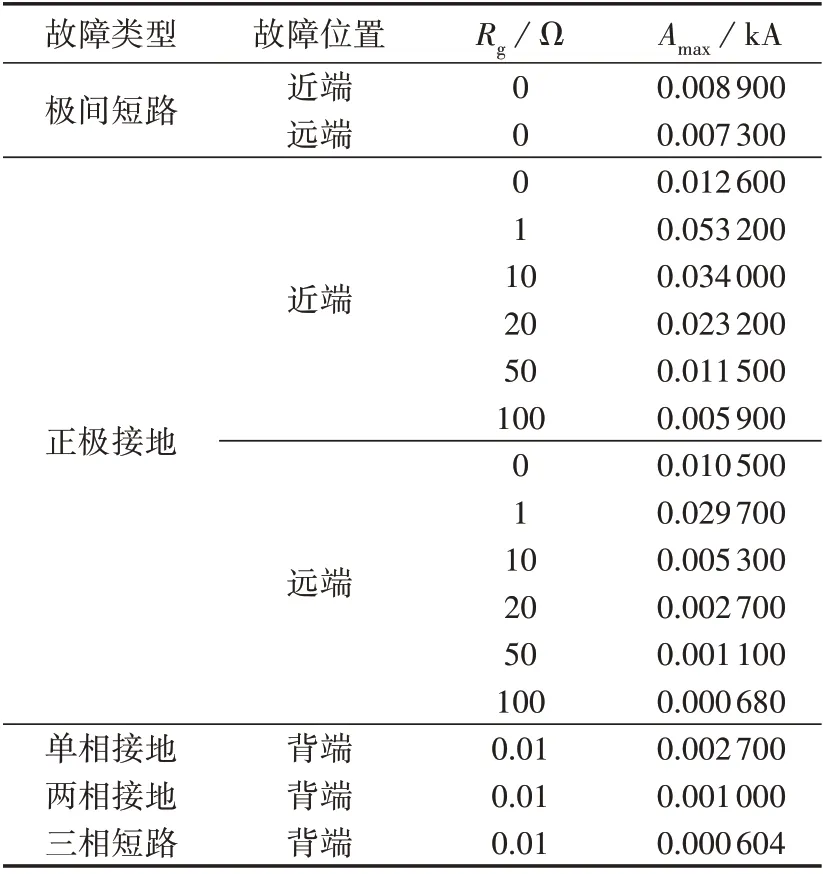
表3 不同故障场景下本文所提故障检测方案结果Table 3 Results of proposed fault detection scheme under different fault scenarios
当线路远端发生经100 Ω 过渡电阻的正极接地故障时,由IEWT 分解所得细节分量c3的模极大值Amax=6.8×10-4kA>Ath=4.2×10-4kA,故障检测的仿真结果如图8所示。图中:Ffault为故障标识,Ffault=1、Ffault=0分别表示发生、未发生故障。
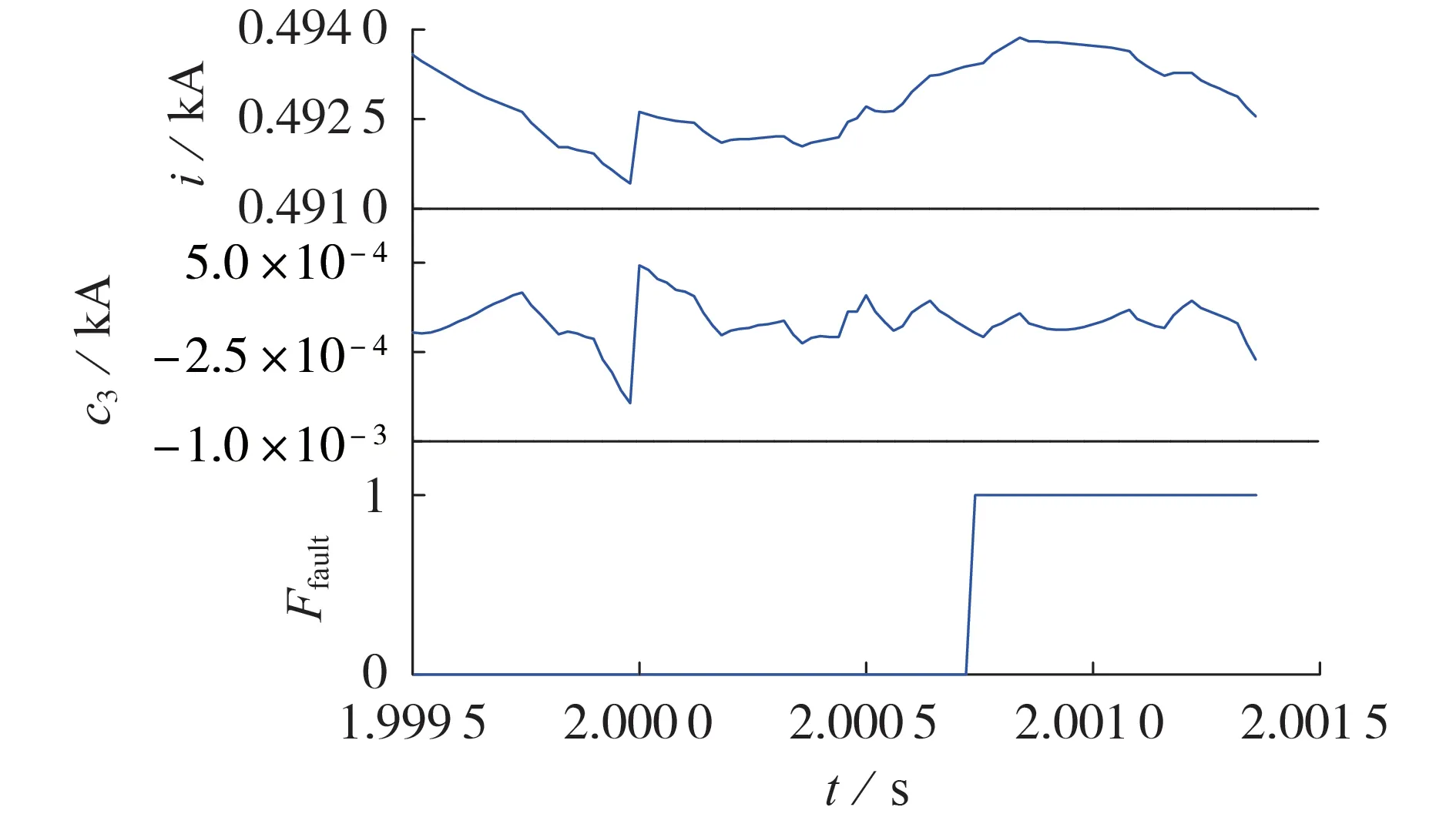
图8 线路远端正极接地故障(Rg=100 Ω)的仿真结果Fig.8 Simulative results of distant positive-pole grounding fault with Rg=100 Ω
由图8 可知,2 s 时刻线路远端发生高阻接地故障时,电流产生突变,但波动幅值甚至小于电流本身的纹波,在此较为极端的条件下,IEWT 仍然能捕捉到电流奇异点,证明其具备较好的高频分量提取能力,且在故障发生后的1 ms 内,本文所提故障检测方案成功地标记了故障。上述分析表明,基于IEWT的故障检测方案具有较强的速动性、短路点过渡电阻耐受能力及远距离故障检测能力。
4.2.2 功率反转时的故障检测性能
设2 s 时刻换流站VSC1、VSC2发生功率反转,在观测线路上监测到的正极电流ip、负极电流in如图9所示。
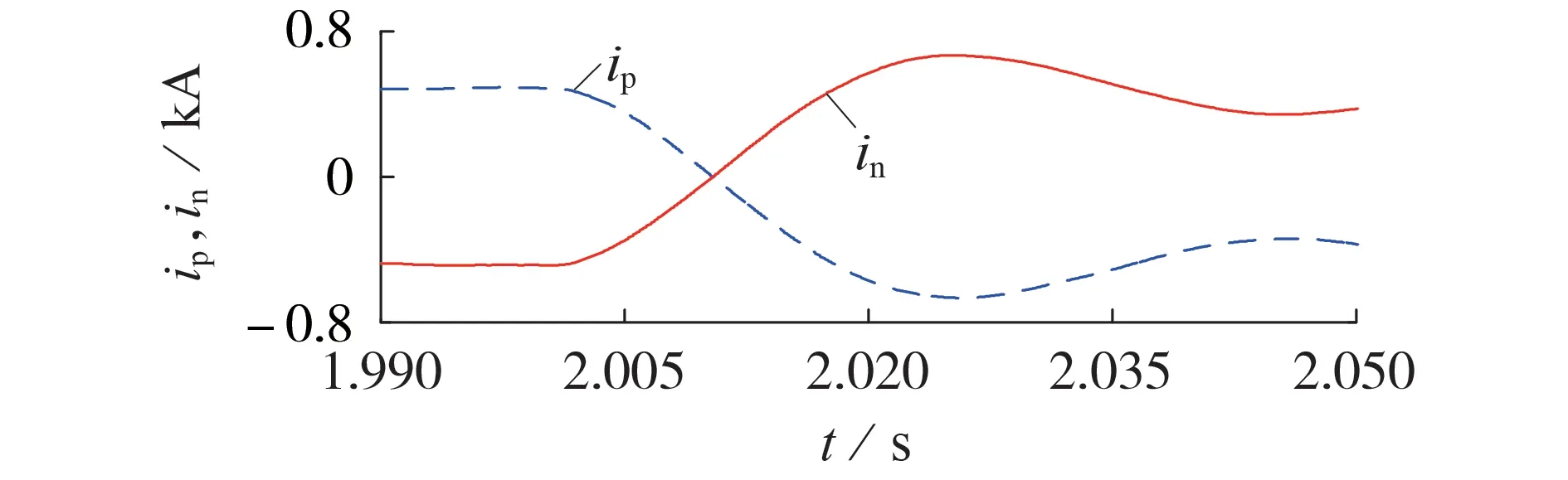
图9 功率反转线路的正极、负极电流波形Fig.9 Waveforms of positive- and negative-pole currents in power reversal line
由图9可知,2 s时刻发生功率反转,各个换流站功率反转导致电流反向,但变化缓慢,电流蕴涵的高频分量较低,IEWT 的分解细节分量c3的模极大值仅为3.2×10-4kA,小于故障检测阈值。因此,设置合适的阈值后,功率反转不会对故障检测方案造成干扰。
4.2.3 负荷波动对故障检测的影响
设图A1 所示网络在1 s 时刻有负荷投入运行,观测线路上监测到的正极电流如图10所示。
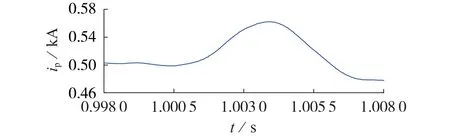
图10 负荷投入时观测线路的正极电流波形Fig.10 Waveform of positive-pole current in observation line when load is input
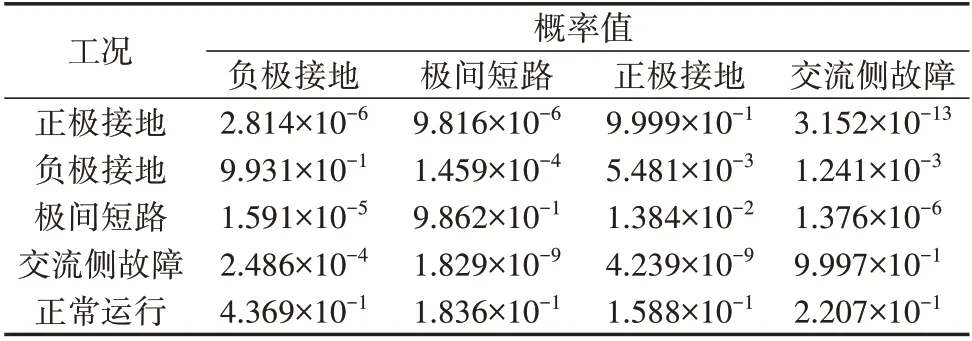
根据图10 可得,l s 时刻负荷投入运行后,观测线路的正极电流缓慢上升,而后逐渐下降恢复至正常,虽然波动程度比高阻接地故障故障情况下大得多,但由于其突变程度较低,IEWT 分解细节分量c3的模极大值仅为1.5×10-4kA 4.2.4 噪声对故障检测的影响 为验证本文所提故障检测方案在噪声环境下的适应性,在电流信号中添加信噪比为20 dB 的高斯白噪声,当VSC2出口处直流线路发生Rg=100 Ω 的正极接地故障时,仿真结果如图11 所示。由图可知,噪声干扰虽然使得由IEWT 分解获得的细节分量c3受到影响,但其仍能准确表征故障,本文方案适应于噪声且依然能够有效检测故障。 图11 噪声环境下本文所提故障检测方案的仿真结果Fig.11 Simulative results of proposed faultdetection scheme in noisy environment 4.2.5 网络结构调整对故障检测的影响 模块化多电平换流器MMC(Modular Multilevel Converter)是一种新型的VSC,具有重要的工程应用前景[18-19]。为验证本文所提故障检测方案在MMC型柔性直流配电系统上的适应性,另外搭建了MMC型手拉手式柔性直流配电系统仿真模型,其与图A1所示网络的区别在于换流站为MMC 型,直流侧采用典型的经箝位电阻接地方式,交流侧采用经电阻接地方式。此外,直流线路采用直流电缆搭建,系统的主要参数见附录B表B2。 设置MMC型柔性直流配电系统MMC2出口处发生经不同过渡电阻的正极接地故障,故障起始时刻为2 s,对应的线路正极电流仿真结果如附录B 图B4所示。基于MMC 的柔性直流配电系统发生单极接地故障时,桥臂电容通过故障点与交流侧接地点组成放电回路,桥臂电流逐渐升高,但由于MMC 换流站直流侧采取大电阻接地方式,且无直流侧集中电容,桥臂过流程度并不高[20]。 按照图7 所示流程,设定Ath=3×10-3kA,仿真验证本文所提故障检测方案对于MMC 型柔性直流配电网的适用性,在4.2.1 节中所设置的不同故障场景下的仿真结果如附录B 表B3 所示。由表可知,本文所提故障检测方案同样适用于基于MMC的直流配电系统,然而在远端高阻接地故障下Amax=3.4×10-3kA,仅略大于设定的阈值3×10-3kA,对判定不利。因此,本文方案应用于基于MMC 的直流配电系统时,对远距离高阻接地故障检测还需做进一步的改善,以提升检测性能。 基于图A1所示网络在不同故障类型、不同过渡电阻、不同故障距离下的故障事件进行仿真,共得到158 组数据。其中:直流线路故障数据包括62 组正极接地故障数据、54组负极接地故障数据和12组极间短路故障数据;交流侧故障数据包括30 组数据。将数据集随机划分为120 个训练集和38 个测试集,依据训练集的训练结果,并考虑保留一定的裕量,最终设置Pth=0.9。 列出其中5 组Softmax 输出的各个故障类别的概率值,如表4所示。 表4 不同工况下Softmax函数的输出结果Table 4 Output results of Softmax function under different conditions 由表4 可知,正确类别的概率值在0.95 以上,而其他类别的概率值几乎为0,两者处于不同的数量级,体现了IMDMF 模型具有较好的特征选择能力和特征增强能力,十分有利于区分各个类别的故障。同时,假设本文提出的检测方案出现了误检测,将正常运行的数据输入故障分类模型,此时Softmax 输出的最大概率值,即Pmax仅为0.436 9,远小于设定的阈值0.9,与各个故障类型的匹配度极低,分类模型输出“未知类型”,因此后续保护动作不会误动,进一步提升了故障检测方案的容错率。 此外,搭建输入环节为多视角数据拼接DSMDMF(Data Splicing Multi-view Deep Matrix Factoriza‐tion)的故障特征提取模型,DSMDMF 模型仅输入环节与本文提出的IMDMF 模型不同,以验证权重自学习网络对模型的贡献,不同模型结构的故障分类结果如表5所示。 根据表5 可得,本文所提IMDMF 模型能准确识别各类故障,且权重自学习网络对分类任务的贡献确实是突出的。当分类模型结构仅有软分配层时,分类精度仅为31.58%,这表明了故障特征提取模块的重要性,也从侧面反映了矩阵分解模块具备较强的故障特征提取能力。 本文提出一种基于IEWT和IMDMF的直流配电网故障检测方案。其中,IEWT能在重构信号不严重失真的情况下捕获到更多的故障能量,更加有利于故障的检测;IMDMF 模型将输入的多视角数据通过权重自学习网络融合,简化了传统MDMF模型结构,有效缩短了模型运行时间,为后续故障处理留足了裕度。仿真结果表明,相比于利用直流线路电抗器电压的故障检测方法,本文方案由于采用了IEWT,仅需采集线路单端的电流、电压,无需安装电抗器,耐受过渡电阻能力较强,且具备检测远距离故障的能力,对于MMC 型直流配电系统亦有较好的适应性;IMDMF 与软分配层相结合组成分类模型能够准确辨识出各类故障,并自动提取故障特征,避免了人工选择的繁琐,更加智能化;同时,本文方案采用概率分布与阈值相结合的方式进行故障分类,可将检测步骤中出现的误判或未知类型故障单独分类,具备一定的容错率,使故障检测分类更加完善。 附录见本刊网络版(http://www.epae.cn)。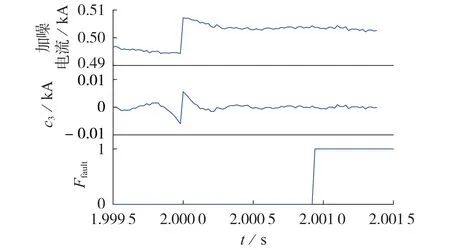
4.3 故障分类模型仿真验证
5 结论
