金属互联中晶粒结构梯度演化及其对力、电性能的影响
2022-06-14张恒嘉张晓敏赵志鹏唐洪武
张恒嘉 ,张晓敏 ,赵志鹏 ,唐洪武
(1.重庆大学 航空航天学院,重庆 400044;2.重庆大学 非均质材料力学重庆市重点实验室,重庆 400044)
随着微电子封装的集成度不断提高,电迁移导致的金属互联失效成为集成电路可靠性的主要瓶颈之一[1]。除了众所周知的质量扩散极性效应外,电迁移作用下晶界(GB)迁移引起的晶粒尺寸演变对金属互联结构的宏观性能的潜在影响也越来越受到研究者的关注。
Albert 等[2]采用X 射线微衍射技术研究了电迁移作用下锡的微观结构演变,发现在恒定电流密度作用下晶界的定向迁移行为导致阳极侧晶粒处于压缩状态,阴极侧晶粒则处于拉伸状态。之后Liang 等[3]用相场法模拟了这一现象,指出晶界的迁移速度与电流密度呈正相关,晶粒的生长行为是由其电各向异性决定的。而对于铜等电各向同性材料,恒定的电流密度对其晶粒尺寸无明显影响[4-5]。与此同时,一些研究表明在诸如焊点和键合线等结构中存在晶粒的不均匀生长行为。如:在Sn-Cu 焊点中,电流在流入和流出Sn 层均存在明显的电流拥挤现象,Cheng 等[6]发现在阳极侧附近的Sn 晶粒相比于阴极侧的更细小。Galand等[7]发现,在恒定温度下,铜互连结构中出现的微孔周围存在更高的电流密度,且该区域的铜晶粒更小。此外,Wang 等[8-9]和Guo 等[10]通过对比银合金键合线在电迁移作用下的正负极形貌还发现,在靠近负极的区域形成了更多的大晶粒,表明较大晶粒尺寸不利于提高合金线电阻。而在键合线的“颈部”同样存在电流密度的集中效应。因此,电迁移作用下晶粒尺寸的梯度分布和电流密度的不均匀性密切相关。材料的力学和电学性能对晶粒尺寸十分敏感,因此晶粒尺寸的梯度化现象对材料性能的潜在影响有待进一步研究。
针对大电流密度下的晶粒结构的梯度化的影响,本文从微观层面出发,通过一套考虑了电迁移效应的相场模型阐明金属互联中晶粒尺寸的梯度化路径。而在宏观层面上,定量表征了晶粒尺寸梯度对材料的力学和电学性能的影响。
1 相场模型
典型的相场模型以系统总自由能泛函的表达式开始,它被定义为体域上v的一个积分。为了描述电迁移对晶界迁移行为影响,在相场自由能泛函中考虑了静电自由能密度项fem:
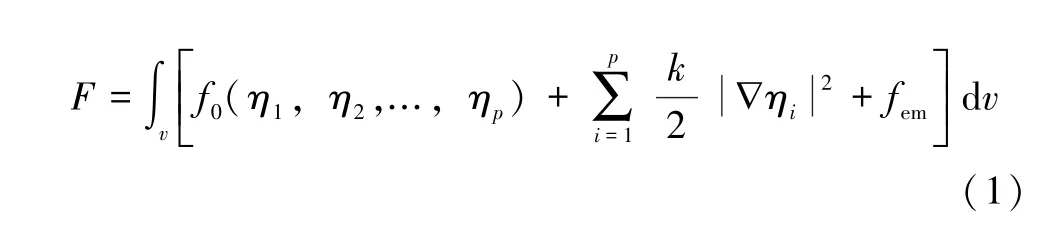
式中:k为梯度能系数;f0(η1,η2,…,ηp)为包含序参数ηi的体自由能密度,可以表示为:
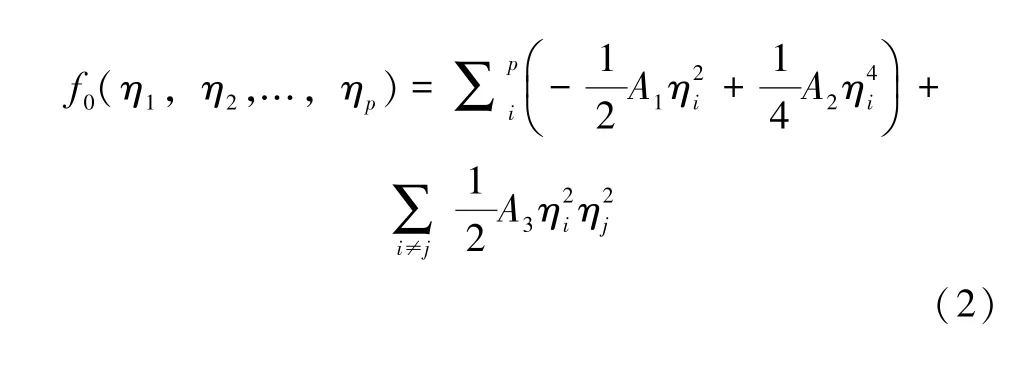
式中:Ai(i=1,2,3)为相场参数;p为晶粒数目;ηi在晶粒i中被设置为1,在其他晶粒中为0。
静电自由能密度fem可以表示为[11]:
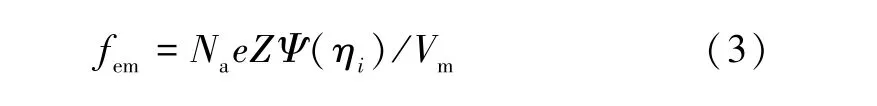
其中,Na,e,Z,Ψ(ηi)和Vm分别为阿伏伽德罗常数、电子电荷、有效电荷数、电势和摩尔体积。电势和电流密度J满足:
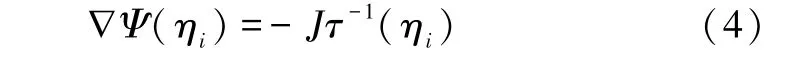
其中,τ为电导率。
非保守场变量ηi的演化能够通过Ginzburg-Landau(G-L)方程来描述:
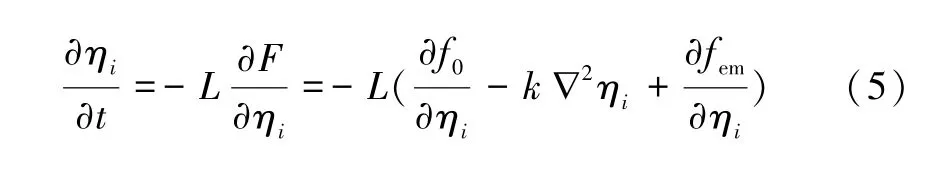
式中,L为晶界迁移率。其取值仅仅影响晶界迁移行为的时间尺度,而不影响晶界迁移的机制,因此为了方便,随后计算结果中的时间是一个加速的度量。
2 计算模型和边界条件
本文使用的计算模型如图1 所示,初始的均匀结构由边长为2 μm 的正六边形晶粒组成,平均晶粒尺寸D(t)=2[A(t)/π]1/2近似计算为3.6 μm,A(t)表示在t时刻的平均晶粒面积。假设电流密度沿x轴分为n段,呈梯度分布。本文所计算目标选取铜,其物性参数为表1 所示。
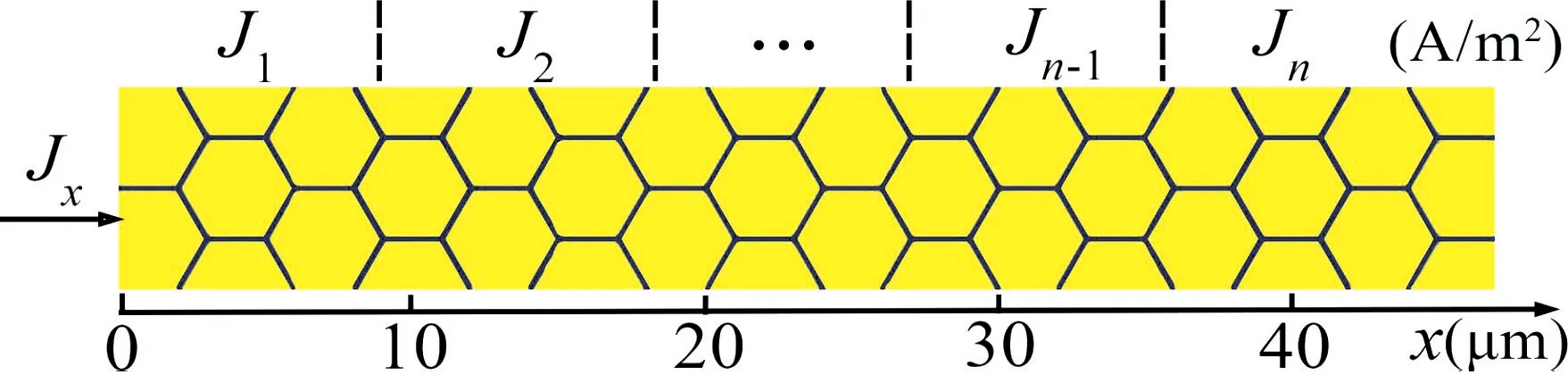
图1 计算模型示意图Fig.1 Schematic of calculation models

表1 铜的物性参数[12]Tab.1 Physical parameters of Cu[12]
3 模拟结果与讨论
3.1 电流密度梯度的效应
首先,将电流密度分为3 段来分析电流密度梯度对晶粒尺寸演化的影响。如图2 所示,保持J1=J3=2.0×108A/m2,通过设置J2分别为2.0×108,3.0×108和4.0×108A/m2来调节电流密度梯度的大小。
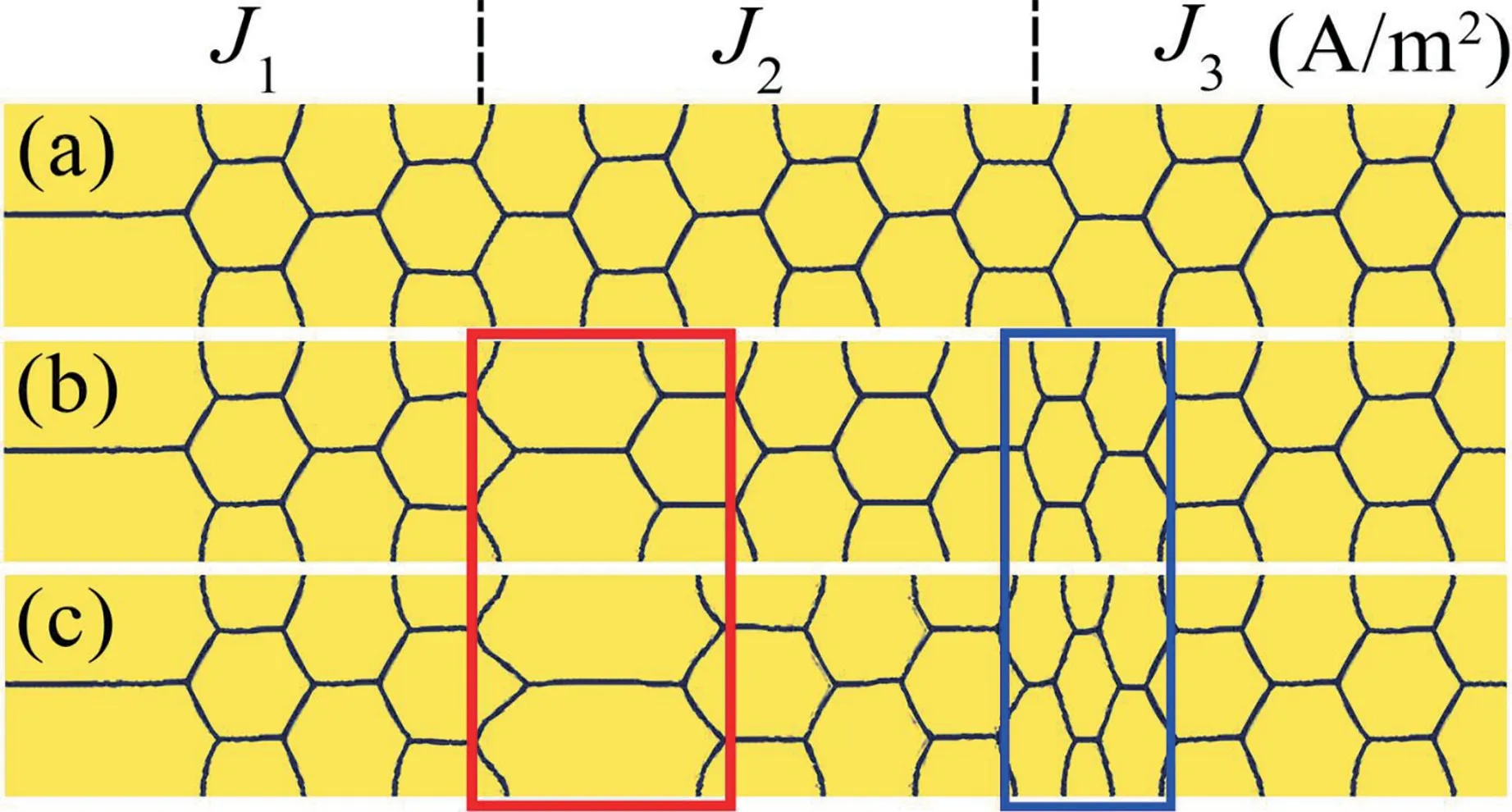
图2 在电流密度梯度作用下t=150 s 时的晶粒相图Fig.2 Phase diagram of grain evolution att=150 s under current density gradients
电迁移作用下的晶界迁移方向与材料的有效电荷数相关,由图2(a)、(b)和(c)所示在t=150 s 时不同电流密度梯度作用下的晶粒演化相图可以发现,对于铜而言,晶界存在向阴极侧的定向迁移行为。已有实验证明当施加恒定的电流密度时,铜晶粒的尺寸无明显变化[4],对应图2(a)的模拟结果。而当存在电流密度梯度时,晶粒尺寸发生了明显变化。在电流密度增大和减小的区域,如图2 中红色框和蓝色框所示,分别发生了明显的晶粒长大和细化现象。可以推测随着电迁移的不断进行,靠近阴极侧的晶粒尺寸会更细小。Liang 等[3]的模拟结果表明,晶界迁移的速度和电流密度的大小呈正相关。因此,当晶界向电流密度更高和更低的区域迁移时,晶界迁移的速度也会成比例变化。最终,在电流密度变化的区域会发生晶界的疏散或堆积效果,从而导致晶粒的不均匀生长行为,这就是电流密度梯度的效应。
3.2 晶粒尺寸的梯度化
在明确了电流密度梯度效应对晶粒尺寸演化的影响后,进一步扩大梯度效应的区域,晶粒尺寸的梯度化也更明显。如图3 所示,增加电流密度的梯度段可以得到一个晶粒尺寸沿x轴呈梯度化分布的结构。
在电流密度整体增大的区域,晶粒随着电迁移的进行发生了明显粗化,如图3 中红色虚线框内演化相图所示;而在电流密度减小的区域,晶粒则被不断细化,如图3 中蓝色虚线框内演化相图所示。此外,将蓝色虚线框内区域定义为细晶层,并计算了该区域晶粒度随时间的演化如图4 所示。细晶层的晶粒数目随着时间增加而不断增加,直到约t=350 s 时晶粒的数目达到了饱和的状态。也就是说,在电流密度梯度作用下,随着电迁移的不断进行,受梯度影响的区域的晶粒尺寸会逐渐梯度化并最终趋于稳定。
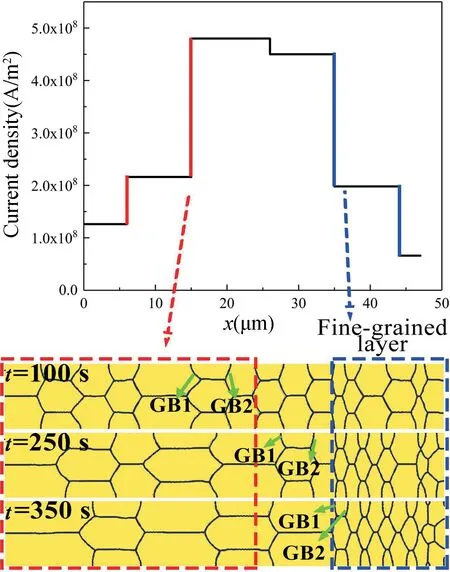
图3 在多段电流密度梯度作用下t=100 s,t=250 s和t=350 s 时刻的晶粒尺寸梯度结构相图Fig.3 Grain size gradient structure phase diagram att=100 s,t=250 s andt=350 s under the action of multi-stage current density gradients
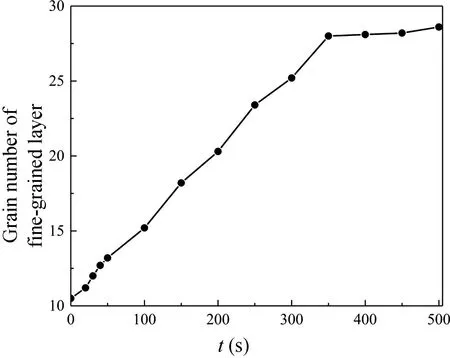
图4 细晶层的晶粒数目随时间的演化Fig.4 Grain number evolution of fine-grained layer with time
为了定量分析电流密度梯度作用下的晶粒尺寸梯度化的机制,本文对晶界迁移的驱动力进行了表征。从图3所示的晶粒尺寸梯度化的过程可以发现,晶界在迁移过程中发生了弯曲,这也更接近实际的情形。一般而言,晶界能够以曲率驱动的方式向曲率中心自发迁移。因此,当前模型涉及曲率驱动力F0和电迁移驱动力Fem两部分,通过计算晶界两侧的化学势的差,可以表示为:
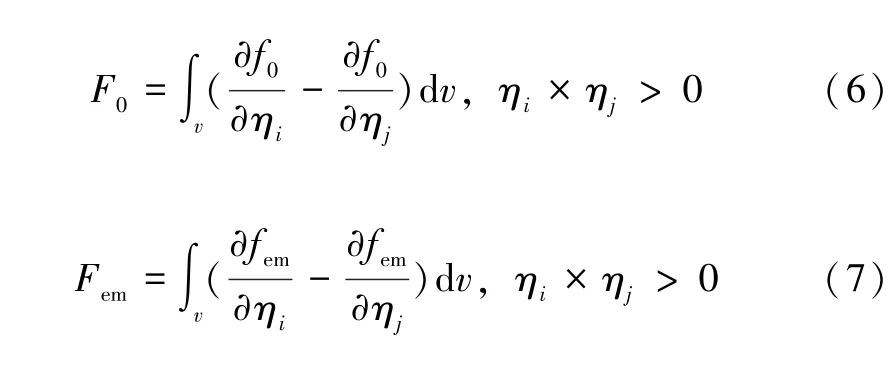
式中,ηi×ηj>0 代表晶界区域[13]。选取图3 中的两条晶界GB1 和GB2 作为代表,给出了两部分驱动力随时间的演化如图5 所示。
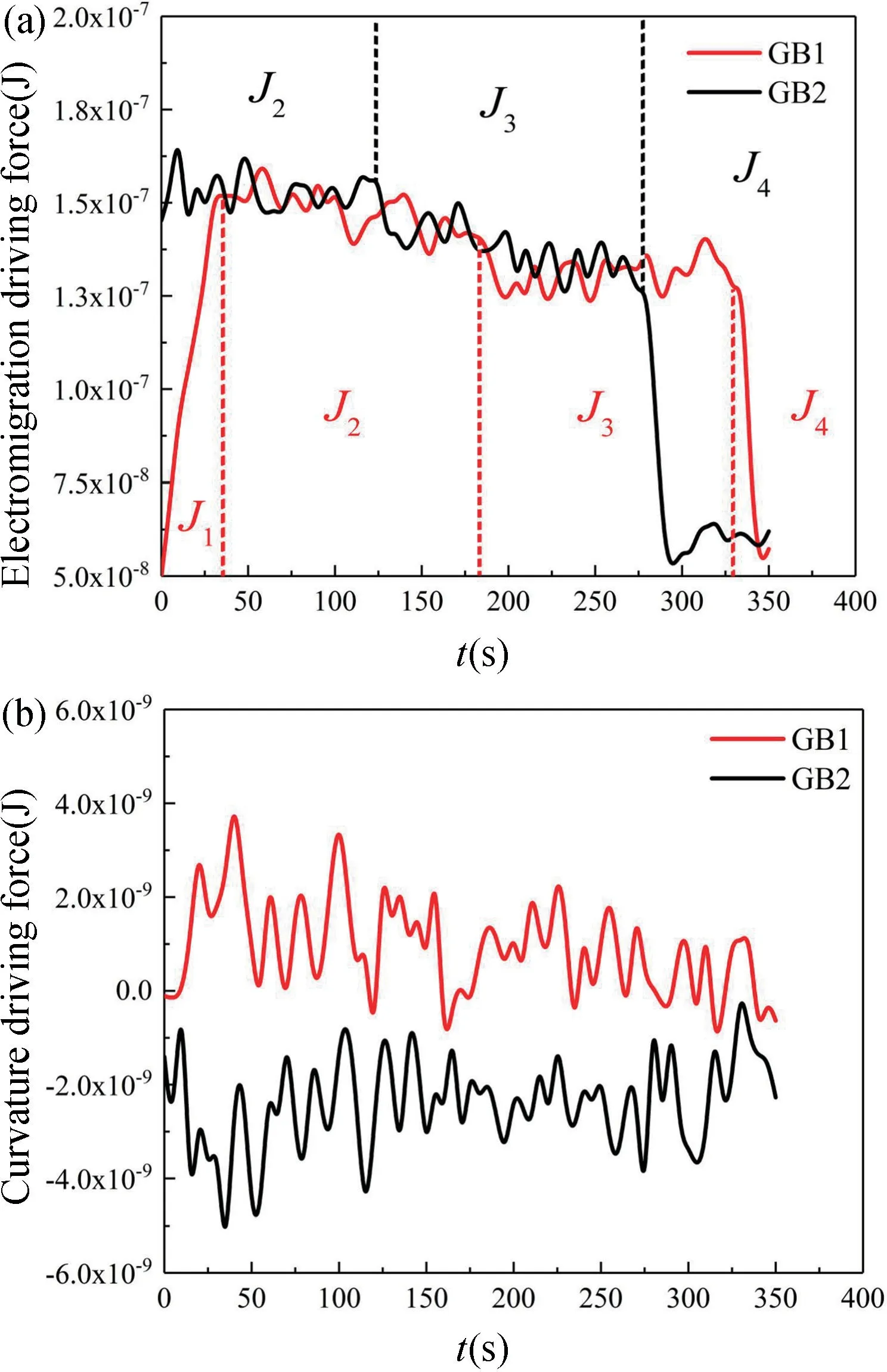
图5 驱动力随时间的演化。(a)电迁移驱动力(J1=2.2×108 A/m2,J2=4.8×108 A/m2,J3=4.5×108 A/m2,J4=2.0×108 A/m2);(b)曲率驱动力Fig.5 Evolution of the driving forces result from(a) electromigration (J1=2.2×108 A/m2,J2=4.8×108 A/m2,J3=4.5×108 A/m2,J4=2.0×108 A/m2) and (b) curvature of GB1 and GB2 shown in Fig.3
显然,图5(a)所示的电迁移驱动力的转折点对应晶界所处区域的电流密度发生变化的时刻,电迁移驱动力变化的幅度决定了晶粒尺寸的跨度。而曲率驱动力的大小与晶界曲率相关,因此,图5(b)所示曲率驱动力随着晶界的形态变化略有震荡,其数值的正负分别表示与电迁移驱动力的方向相同和相反。相比之下,曲率驱动力比电迁移驱动力小1~2 个数量级,因此整个过程中电迁移的效应仍为主导。
4 梯度结构的力学和电学性能的评估
4.1 梯度结构的力学性能评估
针对上一节得到的梯度结构,通过一套基于位错密度的本构方程对其力学性能进行了必要的评估。对于图6 所示的简单拉伸模型,Voigt 混合法则[14]常被用来描述梯度材料整体的应力应变响应。细晶层和粗晶层被视为独立的两层,假设在单轴拉伸载荷下材料各个深度应变相同。梯度结构的总体拉伸应力表示为:
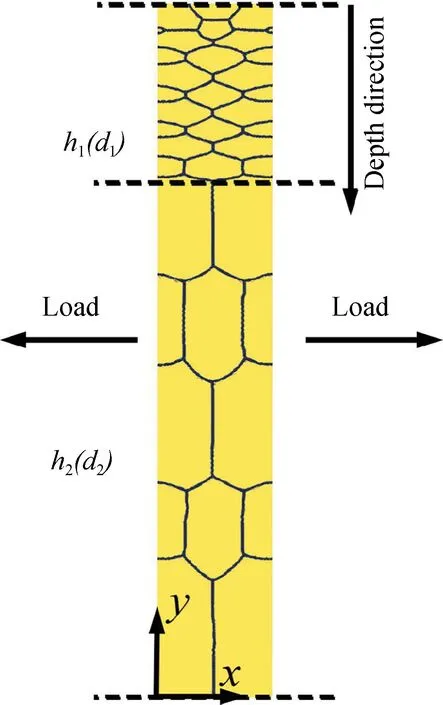
图6 梯度微结构的拉伸示意图Fig.6 Sketch of the gradient microstructure
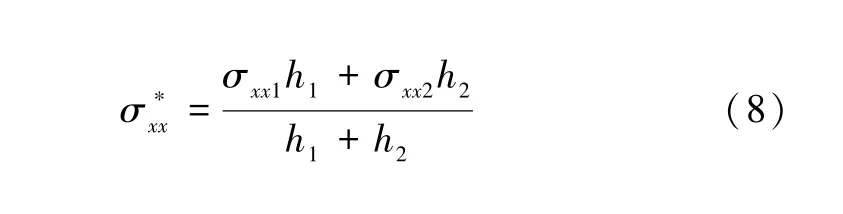
式中:σxx1和σxx2分别为细晶层和粗晶层的应力;h1和h2代表对应层的厚度,分别为12 μm 和35 μm。细晶层和粗晶层的平均晶粒尺寸计算为:d1=1.9 μm,d2=5 μm。
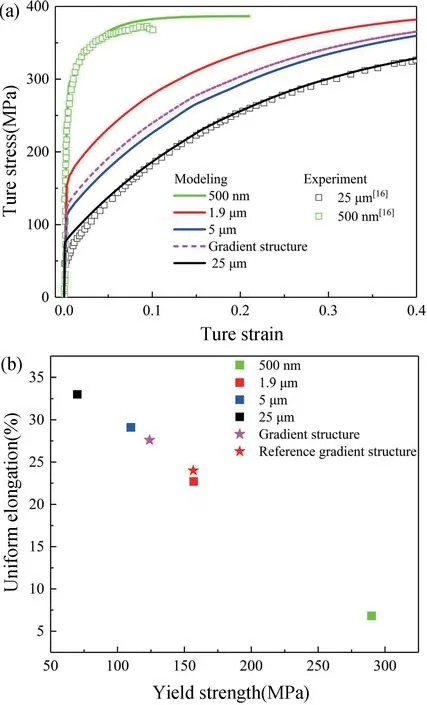
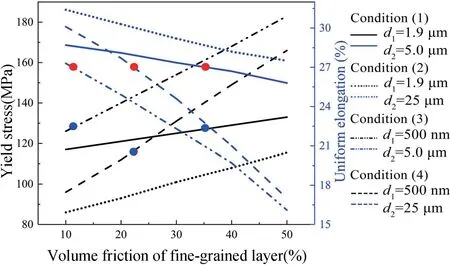
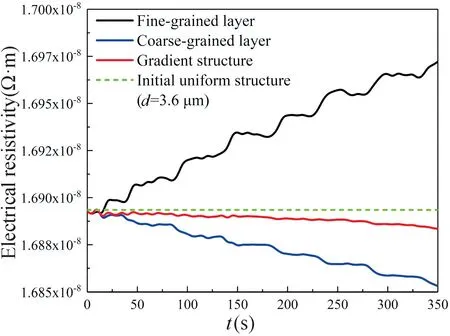
金属的变形机制与晶粒尺寸有关。对于粗晶(d>1 μm)和超细晶(100 nm 式中,前两项表示弹性部分,μ和K分别为剪切模量和体积模量。第三项表示塑性部分,σe=(3sijsij/2)1/2和εe=(2εijεij/2)1/2分别表示等效应力和等效应变;sij=σij-σkkδij/3 为偏应力;m、M、α、b和ρ分别为速率敏感常数、泰勒因子、泰勒常数、Burgers 向量的模和位错密度;σ0为晶格摩擦力;σGB=kHP/d1/2为晶界对流动应力的贡献,其中kHP和d为霍尔佩奇常数和晶粒尺寸;σb=MμbN/d为晶界处位错积累引起的背应力,其中N为晶界处累积的位错数,其随塑性应变εp的演化规律如下: 式中,ω和N∗分别为滑移带间的平均间距和晶界堆积位错的最大数目。 位错密度随塑性应变的演化表示为: 式中:k=k3/ bd();;ke=(de/d)2。k20、和n0为材料参数;k3和ζ分别为与晶粒形状和位错相关的比例因子和几何因子;de表示发生增强动态恢复的临界粒径。模拟中使用的铜材料参数如表2 所示。 表2 铜的材料参数[15]Tab.2 Material parameters of Cu[15] 首先,通过对比平均晶粒尺寸为25 μm 和500 nm的实验结果验证了模型的适用性,进一步计算梯度结构的应力应变响应如图7(a)所示。显然,梯度结构的拉伸响应介于大晶粒尺寸和小晶粒尺寸之间。由如图7(b)所示的屈服应力和均匀伸长率的强度-延性图可以看出,屈服应力随着晶粒尺寸的增大而减小,同时应变硬化能力随之增加。当前模拟获得的梯度结构晶粒尺寸的跨度有限,通过调整细晶层的晶粒尺寸,本文计算了一个参考的梯度结构(d1=500 nm,d2=5 μm)。由图7(b)可发现,和晶粒尺寸为1.9 μm 的均匀结构相比,梯度结构可以达到近乎相同的屈服强度,且表现出更好的韧性。因此,具备晶粒尺寸梯度的结构可以克服强度和韧性之间的折中。 图7 (a)梯度结构和均匀晶粒结构的应力应变响应;(b)梯度结构和均匀晶粒结构的强度-塑性图Fig.7 (a) Comparison of stress-strain response between gradient structure and uniform grain structure;(b) Strengthductility map of gradient structure and uniform grain structure 显然,梯度材料的力学性能对晶粒尺寸的分布很敏感,也就是说,晶粒尺寸跨度和梯度层比例是最直接的控制参数。分别通过调整细晶层和粗晶层的晶粒尺寸以及细晶层的体积分数:d1、d2和f,表征了梯度材料的屈服强度和均匀延伸率,如图8 所示。可以看出,屈服强度和均匀延伸率分别随细晶层体积分数的增加近似线性地增加和减小,曲线斜率随d1减小或d2增大而增大。由此可以推断,细化的晶粒可以提高结构的强度,而粗晶层主要贡献于应变硬化能力和由此产生的延性。此外,还发现存在晶粒尺寸跨度和梯度层比的最优组合,从而产生强度和延性之间的最佳协同效应。例如,对于图8 中的构型(1),(3)和(4),在获得相同的延伸率(27%)(红点)的同时,构型(3)表现出比其他构型更大的屈服强度(蓝点)。因此,基于物理机理建模的方法还可为指导梯度材料的微观结构设计以及提高金属互联结构的可靠性提供理论指导。 图8 屈服强度和均匀延伸率随细晶层体积分数的演化(f=h1/(h1+h2))Fig.8 Evolution of yield stress and uniform elongation with volume friction of fine-grained layer (f=h1/(h1+h2)) 晶粒尺寸对于金属材料的导电性同样有显著影响,通过晶粒细化得到的纳米铜强度相比于粗晶铜提高了约9 倍,但其电导率的损失高达90%[17]。依据Matthiessen 准则[18],铜的电阻率可以表示为: 式中,第一项表示理想无缺陷铜的电阻率,第二项和第三项分别表示晶界和位错相关的影响。SGB表示单位体积的晶界面积。γ0、γGB和γdis的值由相关报道可获得[18-19],分别为:1.68×10-8Ω·m,2.04×10-16Ω·m2和2.3×10-25Ω·m3。 首先,采取式(12)分别计算了晶粒尺寸为100 μm和430 nm 的电阻率分别为:1.681×10-8和2.150×10-8Ω·m,相应的实验值分别为1.690×10-8Ω·m 和2.180×10-8Ω·m[18,20]。通过对比,认为该模型对于当前晶粒结构电阻率的评估是适用的。 假设材料不发生塑性变形,分别表征了粗晶层、细晶层和梯度结构的电阻率如图9 所示。计算结果表明,随着晶粒细化,晶界密度增大,电阻率提高。由于粗晶层表现出较低的电阻率,使得当前梯度结构整体的导电性能提高。在t=350 s 时,稳定梯度结构的电阻率比原始均匀结构降低了0.06%。 图9 梯度结构的电阻率随时间的演化Fig.9 The evolution of resistivity with time of gradient structure 有研究表明[21],对于发生塑性变形的铜,其位错密度一般低于7×1014m-2,其相应贡献的电阻率为1.6×10-10Ω·m,远低于无缺陷铜的固有应变率。因此,当晶粒不断细化,其导电性的损失主要归因于晶界密度的大幅提高,这一行为可能诱发金属互联电气性能的失效。 本文采用相场法模拟了电流密度梯度作用下的晶粒尺寸梯度化路径,并对梯度结构的力学和电学性能做出了评估,得出以下结论: (1)电流密度梯度的存在是金属互联中晶粒尺寸梯度化的主要诱因; (2)梯度结构通过部分细化的晶粒得到强化,而粗晶层则主要为必要的延展性以及防止电气性能失效提供保障; (3)晶粒尺寸的跨度和梯度层的体积分数存在一个最优比例,使得梯度结构在不损失延性的同时提高材料的强度。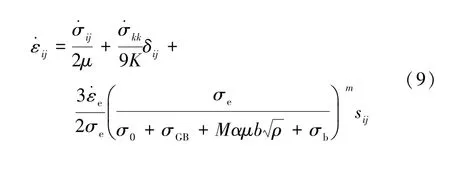
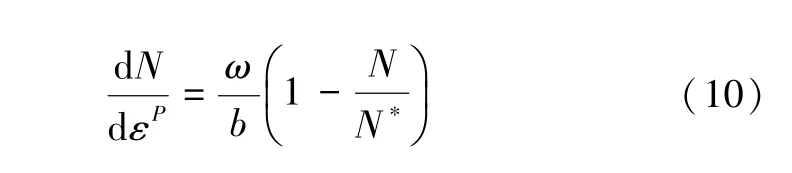
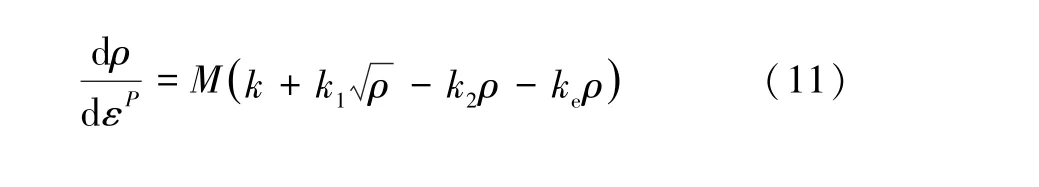

4.2 梯度结构的电学性能评估
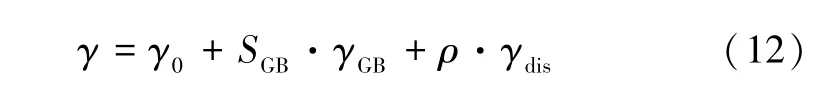
5 结论
