基于分数阶的忆阻Buck-Boost 变换器动力学行为分析
2022-06-14吴朝俊杨宁宁祁永伟
吴朝俊 ,张 琦 ,杨宁宁 ,祁永伟
(1.西安工程大学 电子信息学院,陕西 西安 710048;2.西安理工大学 电气工程学院,陕西 西安 710048)
忆阻器的概念在1971 年被蔡少棠教授首次提出[1],之后在2008 年,HP 实验室首次在物理层面上实现了忆阻器。自此,对于忆阻器的理论研究引起了学者们的强烈关注[2-3]。忆阻器具有独特的记忆功能,被广泛应用于存储器、模拟电路和神经网络中。另外,忆阻器作为一种非线性电路元件,很容易与非线性振荡电路相结合,构建出基于忆阻器的混沌振荡电路。然而,DCDC 变换器作为一种强非线性系统,具有极其丰富的非线性动力学行为。变换器系统参数的选取会导致其产生一些不可预测的现象,比如周期性运动、混沌等[4-8]。电路参数一旦发生变化,系统可能从稳定运行状态进入混沌状态,进而导致系统无法运行甚至发生故障。因此,避免DC-DC 变换器中出现混沌现象,提高系统的稳定性及可靠性在其设计中显得尤为重要。值得注意的是变换器的负载可以是电阻器、电动机或直流电压源,不同的负载对变换器的动态特性影响不同[9]。因此,将忆阻器作为负载引入到DC-DC 变换器中,研究忆阻负载对DC-DC 变换器动态特性的影响,可以为未来忆阻器与电力电子的结合提供一些理论参考。
目前,利用忆阻器替代DC-DC 变换器中的阻性负载进而形成忆阻DC-DC 变换器系统的研究主要集中于电感电流连续的情况。例如Zhang 等[10]将忆阻器与Boost 转换器组合在一起,研究了忆阻Boost 转换器的分叉行为,发现当脉冲周期T变化时,变换器会以电流连续或者电流断续的方式工作。Liu 等[11]研究了具有忆阻负载的压控H 桥逆变器的慢速不稳定性(中频振荡),并且发现这种不稳定性是由于发生Hopf 分岔而出现的。Bao 等[12]提出了一种峰值电流模式(PCM)的忆阻Buck-Boost 变换器,并通过数值和电路仿真研究了忆阻负载对Buck-Boost 转换器的动态影响,其研究结果表明所提出的忆阻Buck-Boost 变换器的稳定工作区域更宽,系统参数的选择范围更广。周晓龙等[13]利用压控忆阻器作为负载,与传统的电流型Cuk 变换器结合,形成了一种新颖的非线性切换电路,发现与常规负载相比,忆阻负载的引入使变换器具有更宽的稳定工作区域。目前,尽管具有忆阻负载的DC-DC 变换器的动力学特性逐渐被深入研究,然而却忽略了系统阶次对忆阻DC-DC 变换器动态特性的影响。上述文献对忆阻DC-DC 变换器的研究完全是整数阶系统,尚未被推广到分数阶系统。
分数微积分理论已经提出了300 多年,其在DCDC 变换器的数学模型建立中发挥着重要的作用[14-15]。研究表明,分数阶模型描述实际系统的特征更为准确[16]。鉴于此,本文将一种有源压控忆阻器作为负载与Buck-Boost 变换器相结合,并将其推广到了分数阶系统。之后利用MATLAB 及PSIM 软件对系统做了数值与电路仿真,分析了分数阶忆阻变换器系统的分岔与混沌。结果表明,分数阶忆阻Buck-Boost 呈现了丰富的动力学行为,且分数阶变换器系统与整数阶相比,稳定工作区域更宽。
1 分数阶微积分概述
分数阶微积分的基本运算符m定义为:
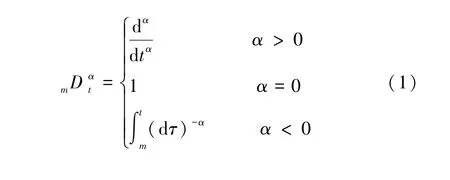
式中:α为分数阶微积分的阶次;t为自变量,m为该变量的下边界;τ为时间变量。Caputo 定义的f(t)分数阶导数如下:

式中:f(t)是关于时间t的连续性函数;n∈N,是不小于α的最小整数;Γ(·)为伽马函数,是一个通过收敛的不定积分定义的关于变量x的函数,其表达式如下:
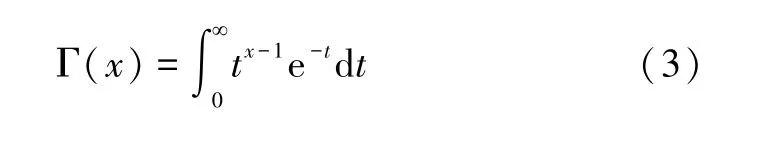
式中,e-t是关于时间t的指数函数。在理想条件下,当α无限接近n时,Caputo 导数就成为了函数f(t)的常规n阶导数。
α阶Caputo 微分算子的Laplace 变换为:
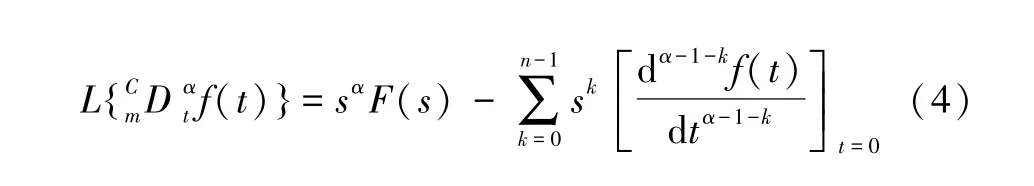
本文分析系统初值为零时的情况,所以Caputo 分数阶导数的Laplace 变换能够简化为:
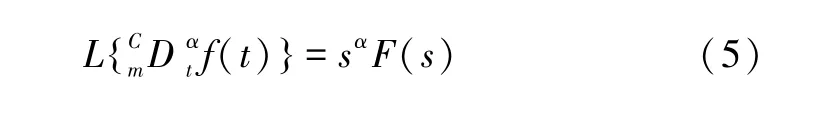
2 忆阻器与忆阻Buck-Boost 变换器的分数阶建模
2.1 忆阻器的分数阶模型
本文Buck-Boost 变换器的忆阻负载通过一个有源压控忆阻器实现,如图1 所示。
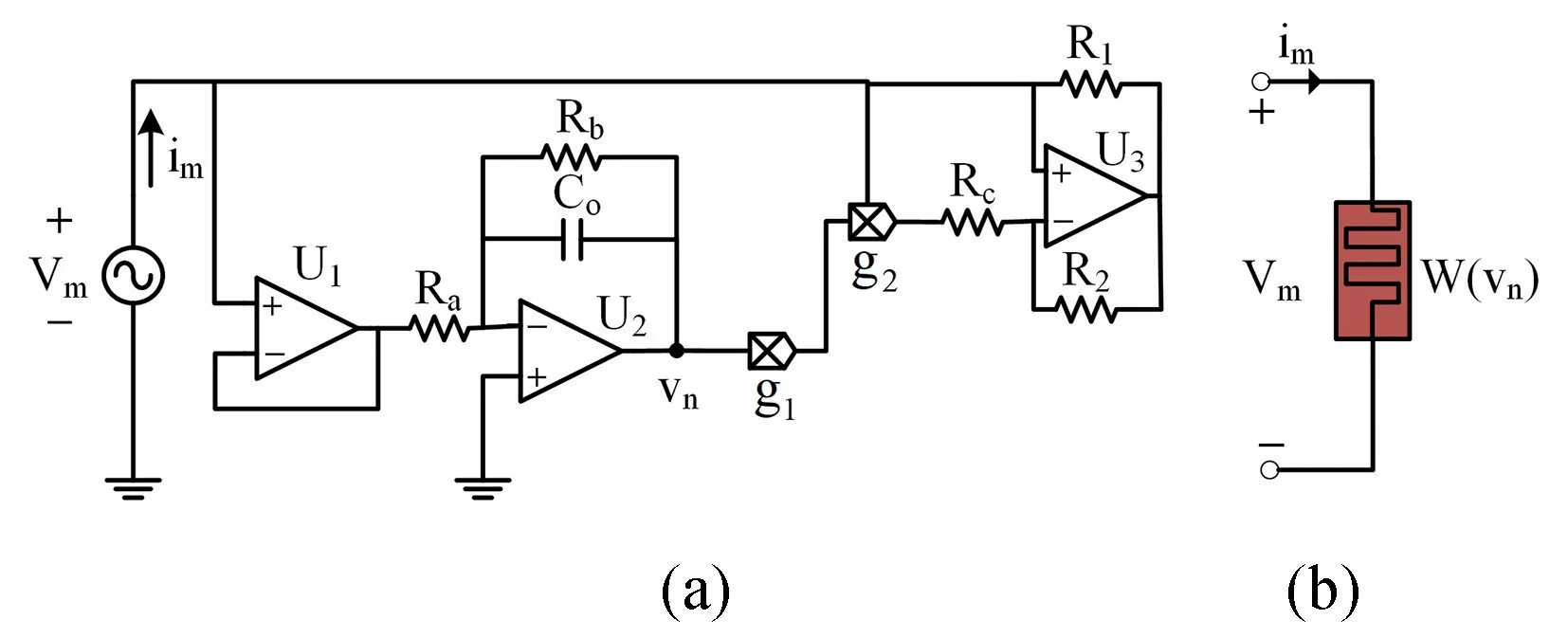
图1 忆阻器等效电路(a)及其模型(b)Fig.1 (a) Memristor equivalent circuit and (b) its model
忆阻器的微分方程为:
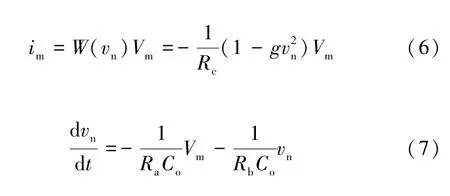
式中:Vm为激励电压;im为输入电流;g为增益g1和g2的乘积;vn为积分电容Co两端的电压。忆阻器的内部函数可写为:
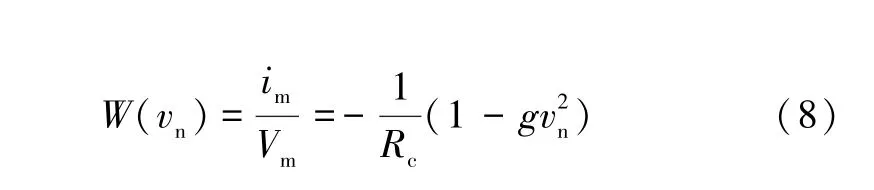
根据分数阶微积分理论,忆阻器中的电容Co能够推广到分数阶的形式。因此,用分数阶电容(其中q为分数阶的阶次)来代替忆阻器中的整数阶电容Co,构成基于分数阶电容器的忆阻电路模型,如图2 所示。

图2 分数阶忆阻器等效电路(a)及其模型(b)Fig.2 (a) The equivalent circuit of fractional-order memristor and (b) its model
由此,分数阶忆阻器的统一数学模型为:

该分数阶忆阻器的各元件参数取值如下:Ra=Rb=6000 Ω,Rc=80 Ω,Co=7×10-9F,g=0.05。在拉普拉斯域中,传递函数F(s)=1/sq可以用来表示阶次为q的分数阶积分算子。采用Oustaloup 所提出的方法获得分数阶积分算子的近似传递函数[17]。当阶次q取值为0.9 时,获得分数阶积分器的近似传递函数为:
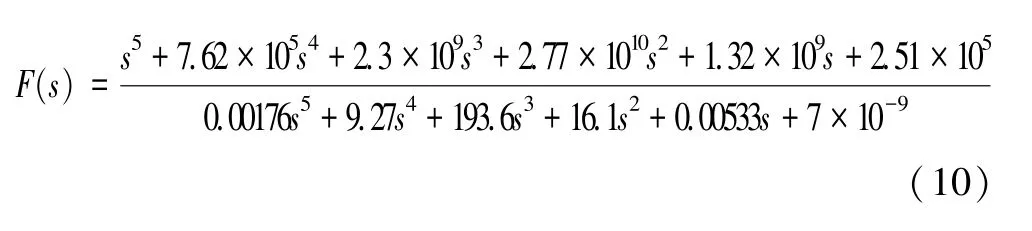
复频域中分数阶电容的等效电路表达式为:

利用图3 中等效单元电路来实现忆阻器模型中的分数阶电容。表1 和表2 分别给出了分数阶电容阶次q=0.9 时,等效单元电路中电阻以及电容的计算值。
表2 分数阶电容等效单元电路中电容的计算值Tab.2 Calculated value of capacitance in equivalent cell circuit of fractional-order capacitor μF

表2 分数阶电容等效单元电路中电容的计算值Tab.2 Calculated value of capacitance in equivalent cell circuit of fractional-order capacitor μF
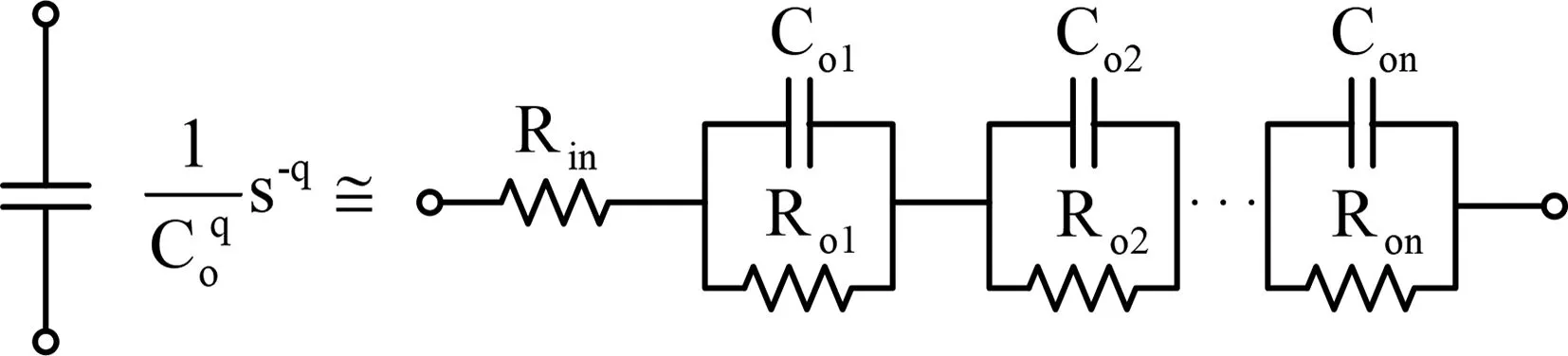
图3 分数阶电容的等效单元电路Fig.3 Equivalent unit circuit of fractional capacitor
表1 分数阶电容等效单元电路中电阻的计算值Tab.1 Calculated value of resistance in equivalent cell circuit of fractional-order capacitor Ω

表1 分数阶电容等效单元电路中电阻的计算值Tab.1 Calculated value of resistance in equivalent cell circuit of fractional-order capacitor Ω
利用MATLAB 对忆阻器的数学模型进行仿真,验证所提出的分数阶忆阻器是否满足忆阻元件的三个基本特性。给定正弦输入电压Vm=Asin(2πf),其中A为激励电压振幅,f为激励频率。当幅值A=12 V,阶次q为0.9,激励频率分别为24,28,32 kHz 时,分数阶忆阻器的Vm-im曲线如图4 所示。由图4 可知,分数阶忆阻器的Vm-im曲线表现为一个在原点收缩的紧迟滞回线。频率增大,紧迟滞回线的面积随之减小。此外,激励频率趋于无限大时,紧迟滞回线更接近于单值函数,从而证明了所提出的分数阶忆阻器满足忆阻的基本特性。

图4 q=0.9 时随频率变化的紧迟滞回线Fig.4 Tight hysteresis loop varying with frequency whenq=0.9
图5 给出了频率与阶次固定,分数阶忆阻器的紧迟滞回线随着输入电压幅值的变化规律。由图5 可知,随着输入电压幅值的增大,紧迟滞回线的面积相应地增大,但其形状并不发生改变。

图5 固定f=24 kHz,q=0.9,不同输入电压幅值下的紧迟滞回线Fig.5 Fixedf=24 kHz,q=0.9,tight hysteresis loop under different input voltage amplitudes
2.2 忆阻Buck-Boost 变换器的分数阶建模
将Buck-Boost 变换器中的纯电阻负载替换成分数阶忆阻器,根据分数阶微积分理论,将Buck-Boost 变换器中电感以及电容扩展为分数阶的形式,这样就得到了分数阶忆阻Buck-Boost 变换器的电路模型。图6给出了电流模式控制下系统的原理图。
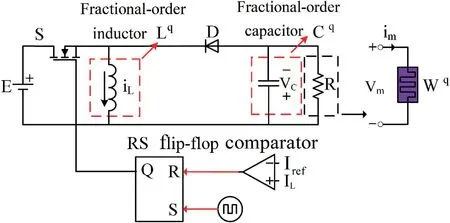
图6 分数阶忆阻器Buck-Boost 变换器原理图Fig.6 Schematic diagram of fractional-order memristor Buck-Boost converter
系统在电流断续模式下工作时:
(1)状态1:开关S 闭合,二极管D 截止,状态方程为
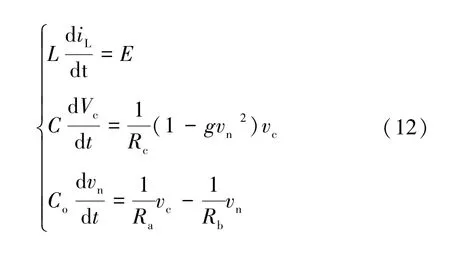
(2)状态2:开关S 断开,二极管D 导通,状态方程为
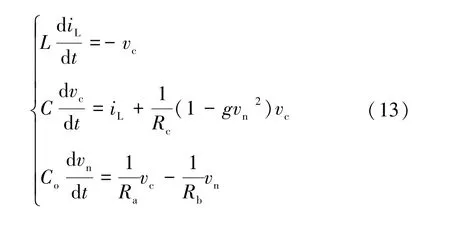
(3)状态3:开关S 断开,二极管D 截止,状态方程为

其中忆阻器两端的电压Vm=-vc。同样在复频域中,分数阶忆阻Buck-Boost 中的分数阶电感Lq的电路表达式为

分数阶电感Lq可以由图7 所示的RL 链式电路来等效,分数阶电容Cq与实现分数阶忆阻器中的电容方法一致。在整个系统中,电路参数设置为E=8 V,L=0.08 mH,C=45 μF,分数阶忆阻器的参数保持不变。另外将整个系统的阶次q设置为0.9,由此可以计算出分数阶电感Lq的等效电阻以及电容的计算值,分别见表3 和表4,在表5 和表6 中分别给出了分数阶电容Cq的等效电阻以及电容的计算值。

图7 分数阶电感的等效链式电路Fig.7 Equivalent chain circuit of fractional inductor

表3 0.9 阶电感Lq的等效电路的电阻参数Tab.3 The resistance parameters of equivalent circuit of 0.9-order inductanceLq Ω

表4 0.9 阶电感Lq的等效电路的电感参数Tab.4 The inductance parameters of the equivalent circuit of the 0.9-order inductanceLq mH

表5 0.9 阶电容Cq的等效电路的电阻参数Tab.5 The resistance parameters of equivalent circuit of 0.9-order capacitorCq Ω

表6 0.9 阶电容Cq的等效电路的电容参数Tab.6 The capacitance parameters of equivalent circuit of 0.9-order capacitorCq μF
3 分数阶忆阻Buck-Boost 变换器的仿真研究和动力学行为分析
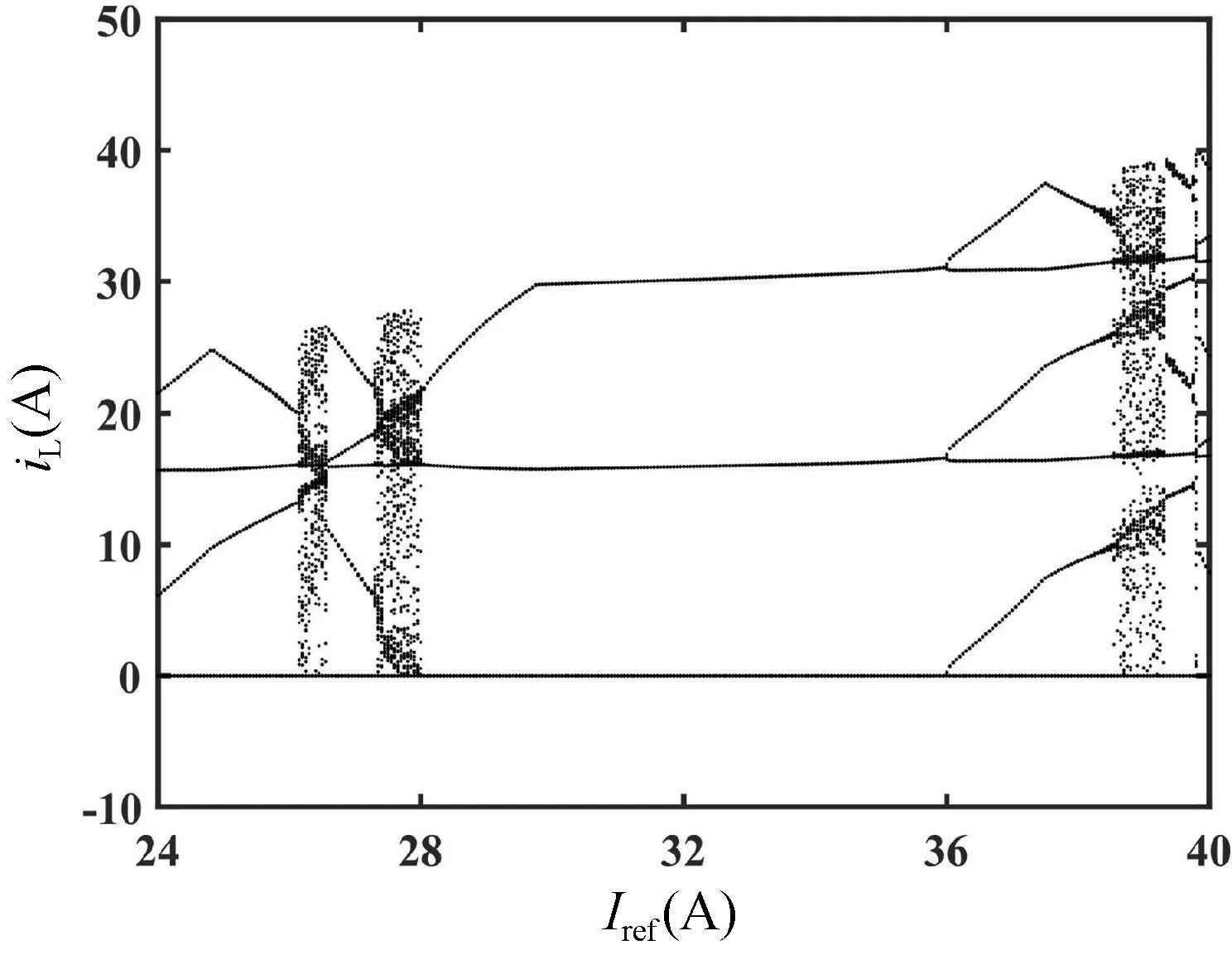
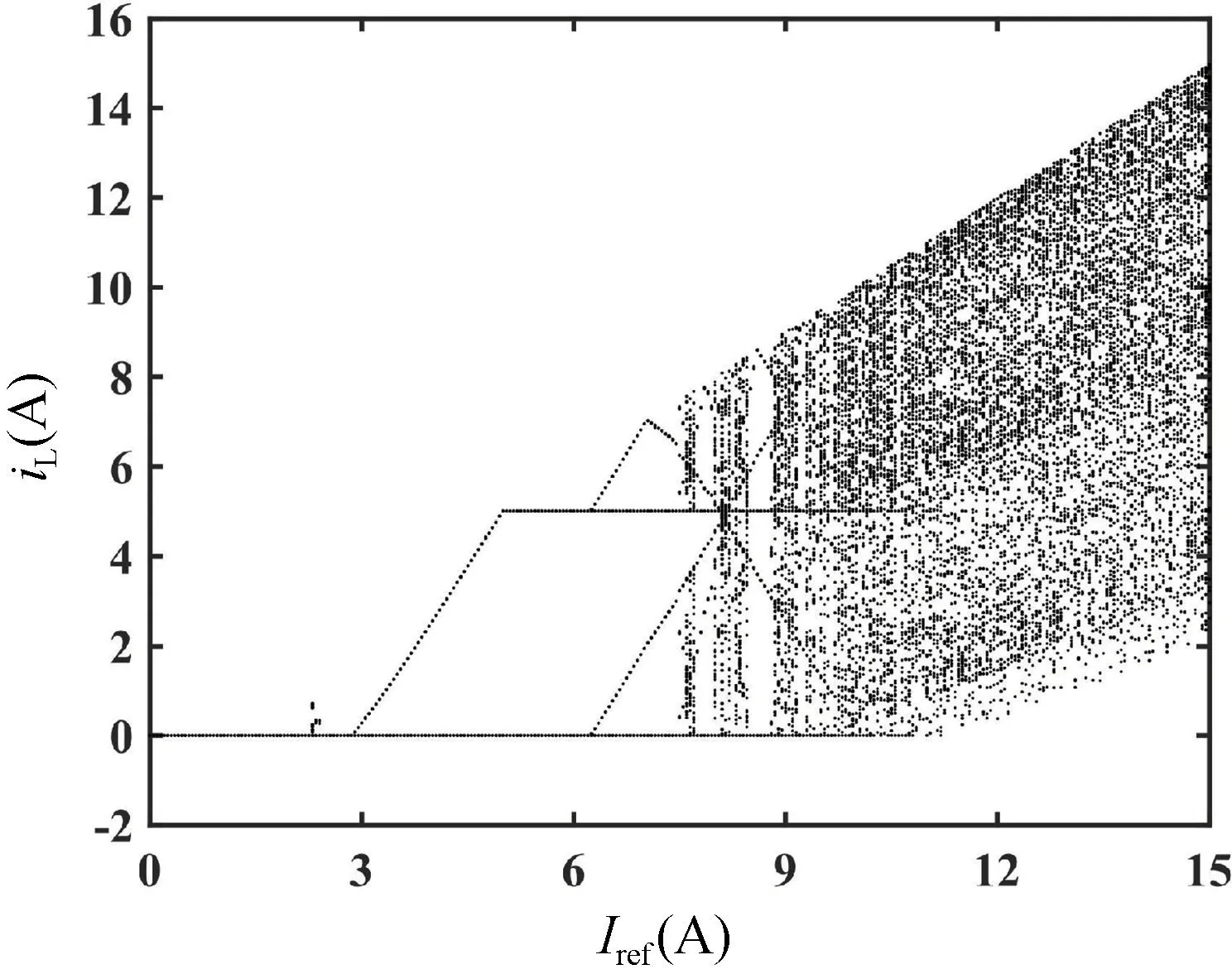
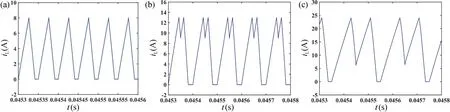
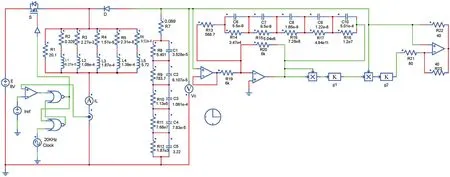
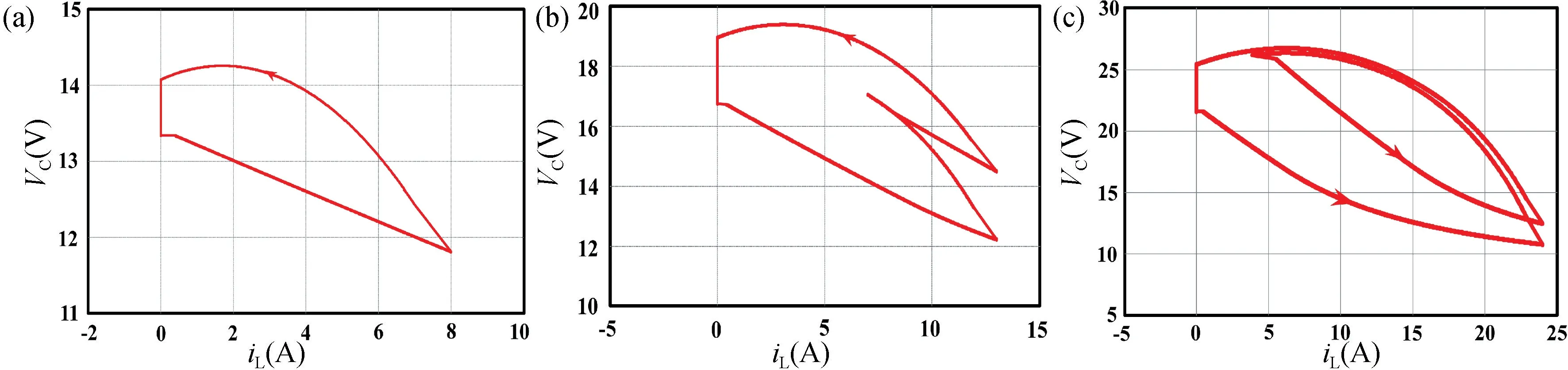
基于式(12)~(14)给出的数学模型,选择参考电流Iref作为分岔参数,通过MATLAB 绘制了电感电流iL随Iref变化的分岔图,如图8 所示。从图8 可以看出,参考电流Iref的大小直接影响整个系统的运行性能。在Iref=10.5 A 时,iL由周期1 状态进入周期2 状态。随着Iref的继续增大,当Iref=22.52 A 时,iL由周期2 状态进入到周期4 状态的分岔。另外,这种分数阶忆阻Buck-Boost 变换器系统的周期分岔与电感电流连续时的周期分岔有所不同。分岔图反映出,当Iref>10.5 A 时,系统电感电流并不是完全工作在电感电流断续的状态,而是在某些时钟周期内存在电流不连续的现象。图9 给出了局部放大的分岔图。由图9 可知,当24 A 图8 分数阶系统以参考电流Iref为参数的分岔图Fig.8 The bifurcation diagram of the fractional-order system with reference currentIref as the parameter 图9 分岔图的局部放大Fig.9 Partial enlargement of bifurcation diagram 另外,当阶次q=1 时,即整数阶忆阻变换器。同样以参考电流作为分岔参数,绘制出整数阶忆阻变换器系统电感电流随参考电流变化的分岔图,如图10 所示。整数阶系统分岔图反应出,当Iref>2.9 A 时,系统由周期1 状态开始进入分岔;当Iref>6.2 A 时,系统开始进入周期4 状态,接着随着参考电流的增大,系统进入混沌态,同样在混沌态之间也存在着周期窗口。分数阶忆阻变换器系统与整数阶系统相比,稳定工作区域更宽泛,参考电流值的选取范围更大。图11 给出了参考电流分别为8,13 和24 A 时,基于MATLAB数值仿真得到的不同周期下的电感电流的时域图。不同周期下的相图如图12 所示。 图10 整数阶系统以参考电流Iref为参数分岔图Fig.10 The bifurcation diagram of integer-order system with reference currentIref as the parameter 图11 基于MATLAB 数值仿真下不同周期时的时域图。(a)Iref=8 A 时周期1 状态下的时域图;(b)Iref=13 A 时周期2 状态下的时域图;(c)Iref=24 A 时周期4 状态的相图Fig.11 The time domain diagrams of different cycles based on MATLAB numerical simulation.(a) The time domain diagram of cycle 1 state whenIref=8 A;(b) The time domain diagram of cycle 2 state whenIref=13 A;(c) The time domain diagram of cycle 4 state whenIref=24 A 图12 基于MATLAB 数值仿真下不同周期时的相图。(a)Iref=8 A 时周期1 状态的相图;(b)Iref=13 A 时周期2 状态的相图;(c)Iref=24 A 时周期4 状态的相图Fig.12 The phase diagrams of different cycles based on MATLAB numerical simulation.(a) The phase diagram of cycle 1 state whenIref=8 A;(b) The phase diagram of cycle 2 state whenIref=13 A;(c) The phase diagram of cycle 4 state whenIref=24 A 利用PSIM 软件对分数阶忆阻Buck-Boost 变换器进行电路仿真验证,电路参数设置与数值仿真参数相同,分数阶电容及电感采用RC 及RL 等效电路,其值在表3~6 已经给出。基于PSIM 软件的分数阶系统电路仿真如图13 所示。图14 给出了分数阶电路系统参考电流分别为8,13 和24 A 时的相图,变换器相应地工作在周期1 状态、周期2 状态及周期4 状态,与理论分析相吻合,进一步验证了理论分析的正确性。 图13 基于PSIM 软件的分数阶忆阻Buck-Boost 变换器电路仿真图Fig.13 The circuit simulation diagram of fractional memristive Buck-Boost converter based on PSIM software 图14 基于PSIM 下不同参考电流的相图。(a)Iref=8 A 时周期1 状态的相图;(b)Iref=13 A 时周期2 状态的相图;(c)Iref=24 A 时周期4 状态的相图Fig.14 The phase diagram of different reference currents based on PSIM.(a) The phase diagram of cycle 1 state whenIref=8 A;(b) The phase diagram of cycle 2 state whenIref=13 A;(c) The phase diagram of cycle 4 state whenIref=24 A 本文将忆阻器作为负载电阻与Buck-Boost 变换器构成忆阻Buck-Boost 系统,并将系统中整数阶电容及电感扩展为分数阶电容及电感,以此来描述实际电容及电感的电气特性。通过数值仿真得到的分岔图及相图表明,分数阶系统工作在电感电流断续模式下时,系统的分岔图与光滑系统存在极大的差别。另外,随着分岔参数的增大,分数阶电路系统并不是经过倍周期到达混沌态,而是由周期态直接进入混沌态。另外,与整数阶忆阻变换器系统相比,分数阶系统具有更宽的稳定工作区域,参数的选取范围更大。最后,在PSIM 中通过采用等效电路的方法实现了分数阶电容和电感的搭建,完成分数阶系统仿真,电路仿真获得的结果与分数阶忆阻Buck-Boost 变换器理论分析及数值仿真结果一致。本文所做的研究为分数阶器件在未来的工程应用中提供参考,同时也为从事忆阻器和DCDC 变换器分数阶建模的学者提供一定的理论依据。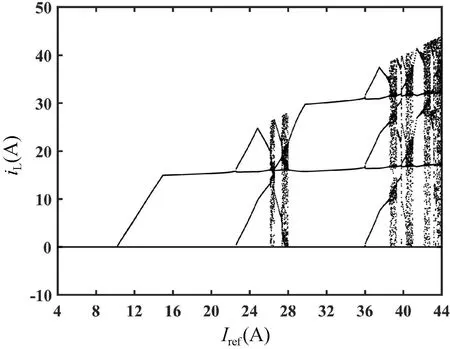

4 系统电路仿真
5 结论
