基于截断球状模型的Fe扭转晶界的能量计算

蒋逸航

（南昌航空大学航空制造工程学院，江西 南昌 330063）

0 前言

晶界作为金属多晶材料内相邻晶粒间的过渡区，是材料组织结构的重要组成部分，会显著影响材料的各项性能。晶界能作为晶界的重要特性之一，它会影响材料再结晶演变过程，同时，还会在相变、再结晶、晶粒长大和许多其他界面相关现象中发挥关键作用。目前，已有许多关于晶界取向参数的研究。杨亮在计算Al与Ni 晶界能时发现晶界能不会随重位因子的改变而呈现一定规律的改变。虽然已经有大量关于晶界能计算的研究，但是大部分都是针对面心立方金属Al 与Ni 的研究，只有极少数研究是针对体心立方金属Fe 的。因此，开展计算体心立方金属Fe 内晶界能的研究具有明确的现实意义。该文将通过分子动力学模拟计算体心立方纯铁扭转晶界（TWGB）的晶界能，从而探究晶界能与取向差轴和取向差角的关系。选定该晶界作为研究对象的原因如下：在面心立方金属Al 与Ni 中已有很多关于晶界的研究，在晶界能计算等方面也有较为全面的认识。TWGB 是常被研究的晶界，但关于计算体心立方金属中的晶界能的研究还不够丰富。

1 模拟方法与参数

该研究将采用分子动力学方法，利用球状模型计算晶界能，文献[5]详细介绍了该模拟方法，其核心内容如下：1） 将取向为g的球状单晶按一定要求转动，分别获得取向为g和g的2 个晶粒（A 和B），沿给定晶界面法向n 将2 个晶粒分别分割成2 个大小相同的半球，随后将晶粒A 和晶粒B 的2 个半球刚性对接成晶粒取向满足取向差Δg=gg的双晶。2） 基于共轭梯度法对能量进行最小化驰豫，使单、双晶具有相同的表面能，也即单晶总自由能（E）与双晶总自由能（E）的差异仅源于晶界，从而使晶界能（γ）等于单位晶界面积上双晶和单晶体总自由能的差。即晶界能γ如公式（1）所示。

式中：S 为晶界的面积。

在球状模型的基础上进行原子删除与引入截断半径R的操作，研究发现，其计算结果会更加精确，将球状分成表层（R > R，R 为半径）和截断内球体（R ≤ R），只将截断内侧的原子用于晶界能计算。在引入原子删除和截断半径后，单、双晶体系具有不同的原子总数，且表层原子的能量不再参与晶界能计算，此时晶界能γ 如公式（2）所示。

该研究在取向差轴（O）空间中，取<100>、<110>以及<111>开始到后面的<331>和<332>轴，一共13 个轴，对于每个O 来说，取向差角θ 从5°开始，以近似5°等间距增加至180°，选取CSL 和非CSL 晶界，至此一共计算了466组数据。通过模拟软件Lammps 进行模拟，选用 2NN-MEAM原子势函数来描述原子的能量和相互作用力。引入块状模型中的原子删除操作会使计算结果更加准确，具体操作可参考文献[5]。由文献[5]可知，5 nm 球状模型对应的R为4.46 nm。

2 结果与讨论

图1 为TWGB 13 个轴的晶界能量图。由图1 可知，不同取向差角对应的晶界能波动比较明显，相同取向差角的晶界所对应的晶界能也存在很大的差异，例如取向差角10°附近的晶界能为553.2 mJ/m～1 022.7 mJ/m。能量低值出现在取向差角91.49°和121.82°附近，其晶界能分别为34.3 mJ/m和37.3 mJ/m， 出现能量低值的原因是晶界处的原子位错重叠，错排程度比其他取向差角更低，因此其晶界能更低。最大晶界能在取向差角45°附近，其晶界能为1 387.5 mJ/m。当取向差角较小时（例如θ<30.1°），晶界能整体随取向差角的增大而增大，与早期的Read-Shockley 公式所描述的结果相吻合。当取向差角进一步增大时，晶界能总体存在一定幅度波动，但总体比较稳定。由晶界的位错模型以及相关的理论可知，晶界能增大的的本质是原子位错密度排列，当取向差角很小时，晶界上原子排列是不规则的，由于晶界是离散的位错构成，且原子密度相对更低，位错排列以及密度都更低，因此其对应的晶界能也会更低。当取向差角慢慢增大时，原子位错排列程度和密度随取向差角的增大而增大，晶界能也会增大。当取向差角不断增大时，构成晶界的位错会相互重叠，位错密度会升高，然而原子之间的作用会导致一部分原子位错湮灭，从而抵消一部分能量，进而使晶界能降低。

图2 为基于TWGB 13 个轴取向差角计算得出的平均晶界能以及R-S 模型计算得出的曲线。由拟合曲线可知，当5°≤θ≤45°时，晶界能随取向差角的增大而增大，其本质是原子位错排列程度和密度随不断增大，使晶界能增大。当取向差角在45°附近时，晶界能达到最大值，其对应晶界能为1 186.4 mJ/m。随后，当角度进一步增大时，晶界能在一定范围内波动，但总体波动幅度不大。但在θ=60°、θ=95°、θ=120°、θ=145°和θ=180°附近能量出现相对更小值。由上述晶界的位错模型的理论可知，该取向差角对应的原子位错密度比其他角度原子位错密度低。综上所述，当取向差角小于45°时，晶界能随取向差角的增大而增大，当取向差角进一步增大时，晶界能有下降的趋势，在1 007.95 mJ/m～1 186.4 mJ/m内波动，但总体趋势比较稳定（波动幅度较小）。

图2 中R-S 拟合曲线为TWGB 能量经最小二乘拟合所得的γ（θ）曲线。基于位错理论的Read-Shockley（R-S）模型常用于对比参照，对R-S 模型来说，不同θ 晶界的能量γ 如公式（3）所示。

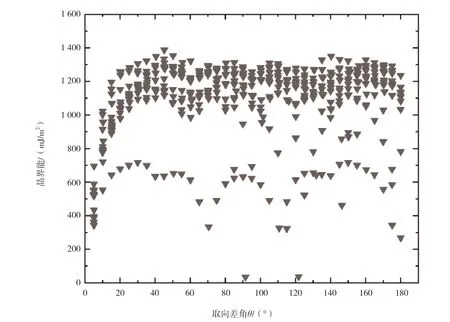
图1 晶界能随取向差角的变化

图2 不同取向差角对应的平均晶界能拟合曲线与R-S 模型拟合曲线

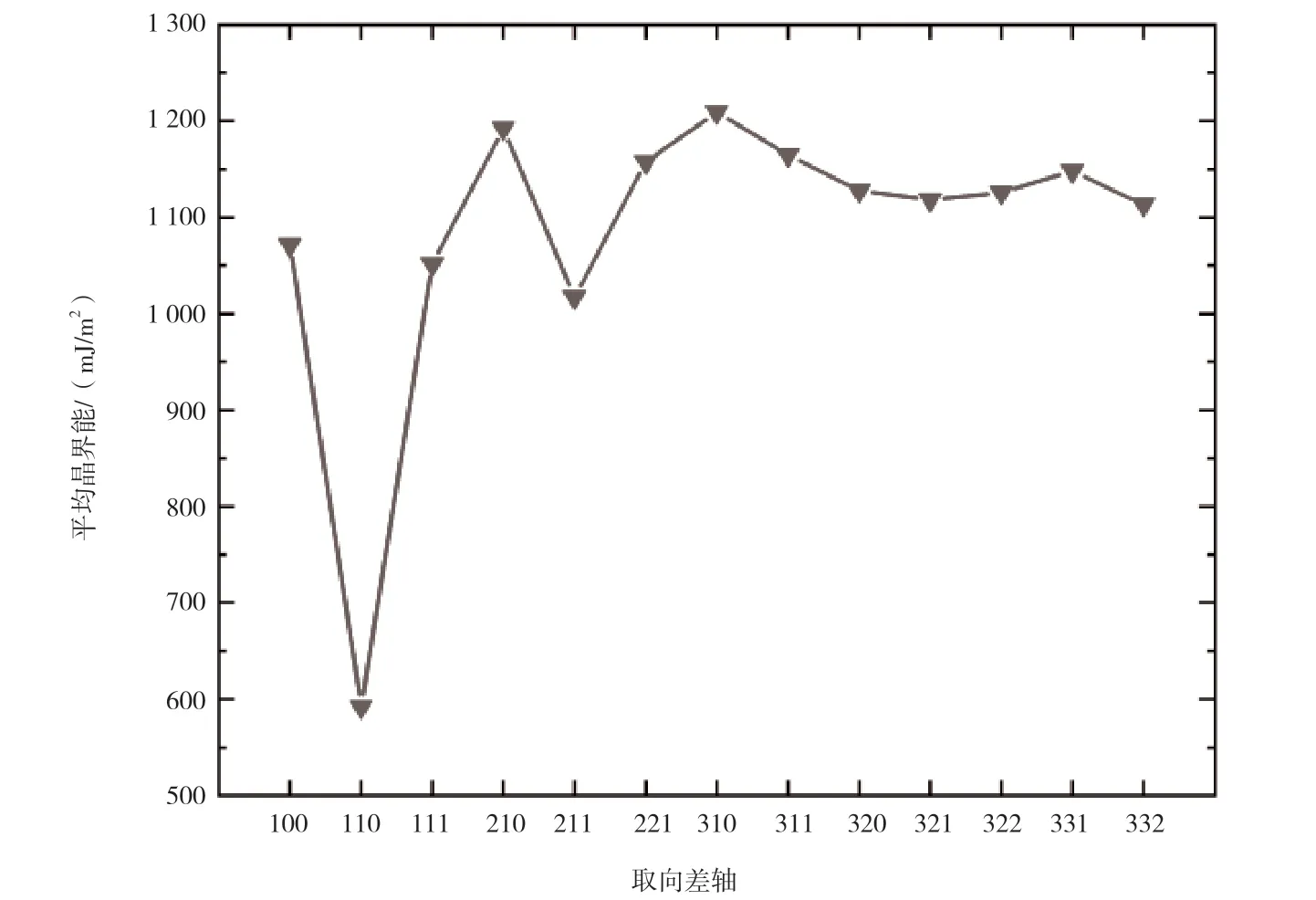
图3 取向差轴对应的平均晶界能

式中：γ和θ分别为拟合γ（θ）曲线上最大晶界能量值和对应的取向差角。

由图2 中的R-S 曲线可知，当5°≤θ ≤45°时，2 组数据拟合所得的能量趋势一致，都随取向差角的增大而增大。当拟合角度大于45°后，该文拟合的数据能量都低于R-S 模型拟合的能量。因为R-S 模型常用于小角度晶界计算，所以仍然可以认为该文的拟合曲线符合预期。

为了进一步探究晶界能与取向差轴的关系，绘制了13个不同取向差轴对应的平均晶界能（如图3 所示）。由图3 可知，不同取向差轴对应的平均晶界能都存在很大的差异，在<110>和<211>2 个轴上出现了能量低值（尤其是在<110>轴，其值更低）。在这13 个轴中，平均晶界能最低的是<110>轴，其对应的平均晶界能为592.2 mJ/m。对图3 上下波动的曲线来说，不同取向差轴无明显规律，需要指出的是，<310>～<332>这7 个轴的平均晶界能比较稳定，波动范围比较小。<100>轴、<110>轴和<111>轴的总体晶界能低于<210>轴、<211>轴和<221>轴的总体晶界能，而<210>轴、<211>轴和<221>轴的总体晶界能低于<310>轴、<311>轴和<321>轴的总体晶界能。由图4中3 条轴取向差角对应的晶界能可知，在<100>轴、<110>轴和<111>轴中，<100>轴和<111>轴2条晶界能曲线波动起伏比较相近，结合图4 可知，2 个轴的波动幅度比较类似，且平均晶界能也比较相同，但不同取向差角对应的晶界能波动比较大。<100>轴的晶界能明显低于<100>轴和<111>轴的晶界能。<100>轴和<111>轴分别在90°和120°附近存在能量极小值，晶界能分别为34.3 mJ/m和34.7 mJ/m。与<100>轴和<111>轴相比，<110>轴的晶界能更低的原因为其内部原子位错密度更低，从而导致晶界能更低。<110>轴其各个取向差角对应的晶界能都低于800.0 mJ/m，但曲线总体更加平稳。综上可知，取向差轴与取向差角对晶界能都存在较大的影响。取向差角对应的晶界能波动会大于取向差轴对应的晶界能波动。

图5 为Fe 扭转晶界的晶界能随重位因子（Σ）的变化图。重位因子定义为单个结构单元重合阵点的数量与总点阵数比值的倒数。由图5 可知，晶界能没有随重位因子值的增大而增大。重位因子越小，其对应的晶界能有高有低，当Σ为某固定值时，其对应的晶界能也有所不同，当Σ 增大时，晶界能波动范围也很大。由此可以看出，晶界能与Σ 不存在线性与非线性的关系。显然，该结果说明基于Σ 预测晶界能高低的方法不可靠。综上可知，晶界能与Σ 并未出现明显的关系。

图4 3 个轴不同取向差角对应的晶界能

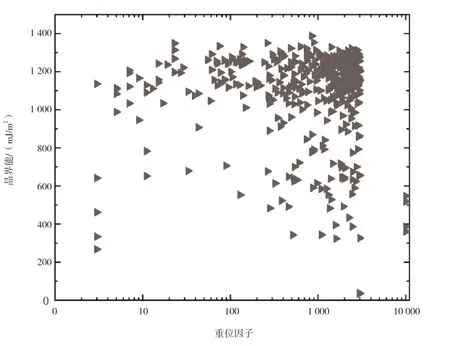
图5 晶界能随重位因子变化

3 结语

在体心立方Fe 扭转晶界中，基于当前计算的13 个轴的晶界能统计结果发现：1） 在当取向差角小于45°时，晶界能随取向差角的增大而增大，当取向差角进一步增大时，晶界能出现先下降后上升的趋势，但总体趋势比较稳定。在θ=60°、θ=95°、θ=120°、θ=145°和θ=180°附近存在能量低值，但总体波动不大。该趋势与R-S 模型计算的晶界能趋势比较一致（尤其在θ ≤45°范围中）。2） 不同取向差轴对应的晶界能存在差异。在取向差角与取向差轴2 个参数中，取向差角对TWGB 能量的影响更大。3） 晶界能与重位因子（Σ）整体上不存在相关性，同Σ 值对应不同的晶界能，Σ 值不能预测晶界能的高低变化。