一桥横跨南北，“曲直”变通途

杭仁礼 张毅

[摘  要] 《普通高中数学课程标准（2017年版2020年修订）》中对数学文化给予了高度重视，强调要将数学文化融入数学教学活动中，让学生了解数学的发展历程，认识数学文化在科学技术和人类社会发展中所起到的重要作用，引导学生认识和感悟数学的科学和文化价值. 文章主要论述了如何利用祖暅原理将求解旋转体和多面体体积达到完美柔和.

[关键词] 祖暅原理;多面体;旋转体

初遇问题

在备课过程中，笔者提出：能否构造一个完整的几何体可以直接求得球的体积呢？鉴于球是高度对称的几何体，起初笔者设想构造一个正四面体ABCD，棱长为a.

如果想要利用祖暅原理，構造的几何体必须满足三个条件：

①构造的几何体与球等高;

②构造的几何体与球的体积相等;

③将构造的几何体与球放置在同一水平面，用平行于水平面的平面去截几何体和球，得到的截面积处处相等.

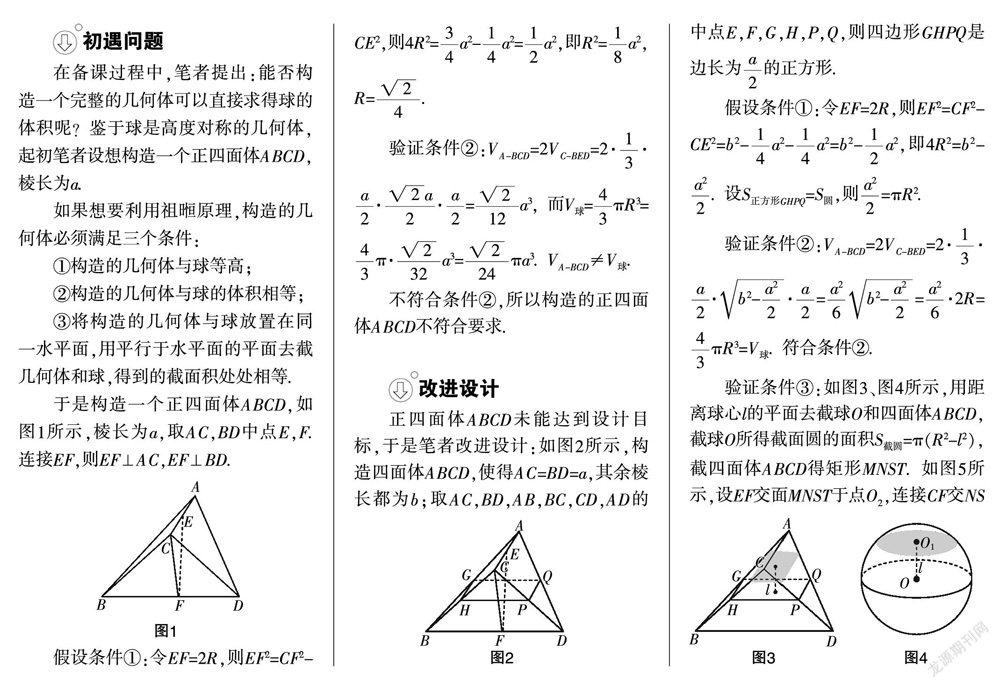
于是构造一个正四面体ABCD，如图1所示，棱长为a，取AC，BD中点E，F. 连接EF，则EF⊥AC，EF⊥BD.

不符合条件②，所以构造的正四面体ABCD不符合要求.

改进设计

如此，笔者便实现了构造一个多面体、一次性求得球的体积的设想，那么，这样的结论能否加以推广呢？

推广结论

1. 求椭球（椭圆绕其对称轴旋转一周所得的几何体）的体积

方法1：推广课本的方法，构造几何体（将圆柱挖去同底等高的倒置圆锥得到的几何体）.

为此，构造底面半径为b，高为a的圆柱，从圆柱中挖去一个以圆柱右底面为底面，左底面圆心为顶点的圆锥（如图7所示），把所得的几何体与半椭球放在同一个竖平面上.

方法2：构造四面体，一次性完整推导椭球的体积.

构造四面体ABCD，使得AC=BD=m，其余棱长都为n.

上述都是封闭曲线所得的旋转几何体，如果是半开放曲线绕旋转轴旋转一周所得的几何体，又该如何求解其体积呢？

2.构造三棱柱，求解抛物线绕其对称轴旋转一周所得几何体的体积

已知抛物线y=x2（0≤y≤m），绕y轴旋转得到几何体Z，求该几何体的体积.

祖暅原理的内容浅显易懂，只要能构造出可求体积的几何体，就能求出所需求的几何体的体积.中华数学文化博大精深、资源丰富，笔者只是从构造多面体的角度求解论证了一些常见的旋转体的体积，在教学过程中就感悟到了中华优秀传统文化的历史自豪感. 这一原理的深化，便是现代高等数学微积分思想.