略谈“算法初步”教学的几点建议

蒋永录

[摘  要] “算法初步”是新课标新增内容，在高中数学中具有一定的地位. 结合教学实践，提出几点教学建议，即把握全局，突出素养;着眼细节，发展能力;放大文化，凸显价值.

[关键词] 算法初步;高中数学;建议

“算法初步”是新课标新增内容，它的课程目标是在学生已有的数学知识的基础上，引导学生用算法思维解决问题，从而提高学生数学思想的应用能力，为学生将来的发展空间提供后备知识. 它在高中数学中具有一定的地位. 然而，“算法初步”毕竟是“算法知识”，教学中教师应如何把握好“度”呢？教学中应侧重哪些知识点？在此，笔者提出了几点教学建议，供同仁们参考，不当之处敬请斧正.

[⇩] 把握全局，突出素养

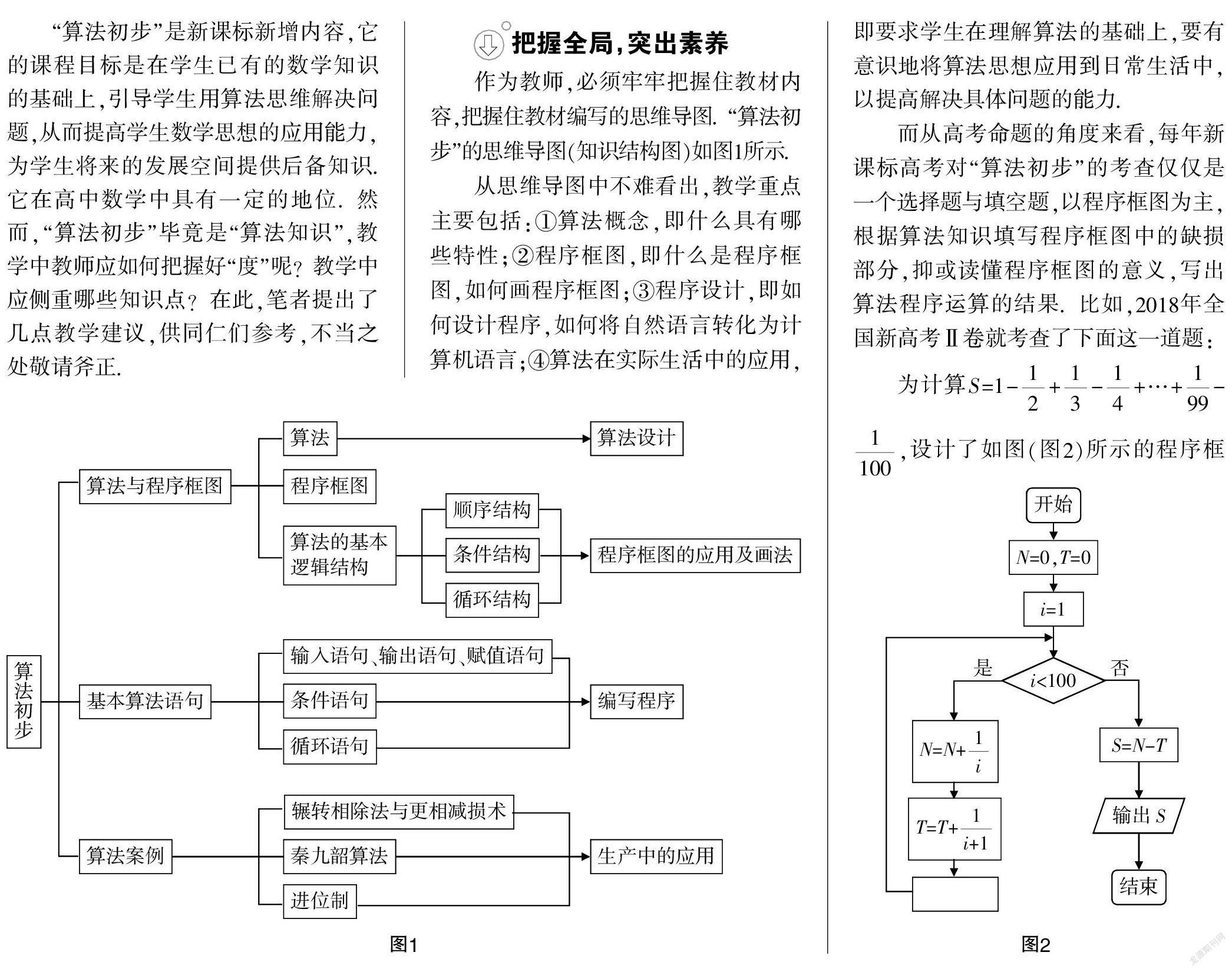
作为教师，必须牢牢把握住教材内容，把握住教材编写的思维导图. “算法初步”的思维导图（知识结构图）如图1所示.

从思维导图中不难看出，教学重点主要包括：①算法概念，即什么具有哪些特性;②程序框图，即什么是程序框图，如何画程序框图;③程序设计，即如何设计程序，如何将自然语言转化为计算机语言;④算法在实际生活中的应用，即要求学生在理解算法的基础上，要有意识地将算法思想应用到日常生活中，以提高解决具体问题的能力.

而从高考命题的角度来看，每年新课标高考对“算法初步”的考查仅仅是一个选择题与填空题，以程序框图为主，根据算法知识填写程序框图中的缺损部分，抑或读懂程序框图的意义，写出算法程序运算的结果. 比如，2018年全国新高考Ⅱ卷就考查了下面这一道题：

为计算S=1-+-+…+-，设计了如图（图2）所示的程序框图，则在空白框中应填入（  ）

A. i=i+1 B. i=i+2

C. i=i+3 D. i=i+4

此题要求考生模拟程序框图的运行过程：S=N-T=

1-

+

-

+…+

-

;累加步长是2，则在空白处应填入i=i+2. 故选B.

从解答过程来看，本题在高考题中属于送分题，这种命题模式正体现了“初步”两字，本无可厚非. 但对这一章的教学仅仅是为了应考吗？笔者认为“否”. 本章教学，教师应站在素质教育和数学核心素养的培养的高度展开，为学生的全面发展打下基础. 比如，可以让学生就同一个事件，从不同角度设计不同的算法，如“有8个小球，其中7个重量相同，仅有一个较重，用天平如何称出哪个是较重的小球？”虽然教材不要求学生熟练地掌握算法设计，但这类问题往往能引发学生的兴趣，教师可以抓住时机，让学生从不同的算法设计中感知优化算法的重要性，从而提高学生逻辑推理与数学建模等数学素养.

[⇩] 着眼细节，发展能力

数学教学的目的是培养学生的数学能力，既然“算法初步”属于新课标数学的教学内容，因此发展数学能力也是该课程的最终目的. 阅读教材不难看出，“算法初步”不是孤立的数学内容，而是与其他知识有着紧密的联系：可以是“算法初步”背景下的数列问题，可以是“算法初步”背景下的函数问题，可以是“算法初步”背景下的三角问题，还可以是数列背景下的“算法初步”问题，等等. 关注每个算法问题的细节，其实就是关注算法与其他知识的交汇，这类问题的解决，不仅能提高学生算法的应用能力，更能提高学生数学知识的综合应用能力.

例如：程序框图如图（图3）所示，当输入n=3时，输出的S的值为（  ）

A. B.

C. D.

分析：第一次循环：S=，i=2;第二次循环：S=+，i=3;第三次循环：S=++，i=4，满足循环条件，结束循环. 故输出S=++=

1-+-+-

=. 故选B. 本题考查算法的同时，又考查了裂项相消法求数列之和.

又如：在实数的原有运算法则中，我们补充定义新运算“”，其中S=ab的运算原理如图（图4）中算法语句所示，则集合{y

y=（1x）·x-（2x），x∈[-2，2]}（注：“·”和“-”仍为通常的乘法和减法）的最大元素是（  ）

A. -1  B. 1  C. 6  D. 12

分析：利用算法语句和新定义得出函数的解析式，再结合函数的性质求解.

由算法语句得S=ab=b2，a<b，

a，a≥b，所以y=（1x）·x-（2x）=x3-2，1<x≤2，

x-2，-2≤x≤1，其在[-2，2]上单调递增，所以当x=2时，y取得最大值6，即集合中最大元素是6，故选C. 本题将“算法初步”与创新函数综合在一起考查学生，更加突出学生的综合素质与数学能力.

对“算法初步”的教学内容，教师应站在“大数学”的角度看待它，用联系的观点看待它，用发展的眼光审视它，着眼于每个细节，在每个细节上挖掘培养学生数学能力的价值. 这样的教学，不仅有利于学生应试能力的提高，更能培养学生的综合能力.

[⇩] 放大文化，凸显价值

数学具有文化特征，是一种传统的文化. 因此，数学有着深厚的文化底蕴与广泛的应用价值. “算法初步”更是如此. 教师应该抓住其文化价值，以此来培养学生的学习兴趣.

例如：一队士兵有n个人，他们想过河，岸边有一只小船和两个愿意帮助他们过河的小孩，无论是士兵还是小孩，他们都会划船，但由于小船承载力较小，一次只能承载两个小孩或一个士兵，请大家开动脑筋，设计一个能让这n个士兵都能到河对岸的运作方案.

本题引发了学生极大的兴趣，纷纷跃跃欲试，通过尝试，学生体会到：设计一种合理可行的算法，首先要明白算理，既要清楚方法，又要理清步骤. 自然语言能十分细致地表述想法，框图则能从结构上直观清晰地反映出想法流程，而程序语句是为计算机“量身定做”的，是一种计算机语言，它们之间既有区别又有联系，我们应学会不同语言之间的转化.

又如：某工人师傅砌墙，砌第一层墙他用了全部砖的一半多一块;砌第二层墙他用了剩下砖的一半又多一块，以后他砌每一层墙都用了前一层砌完后剩下砖的一半多一块，到第二十层时恰好剩下一块砖，将其砌上，这堵墙也就砌完了.画出计算这堵墙用砖块数的程序框图并编写程序.

此题更是从算法角度诠释数列问题，体现了算法的实际应用价值.

在教材的“算法案例”中，处处洋溢着数学文化，如韩信点兵、辗转相除法、进位制等，都是极好的传播数学文化的原始教材，教师一定要用足用好. 同时我们也应该看到，数学文化与“算法初步”的数学问题应运而生，应引起关注.

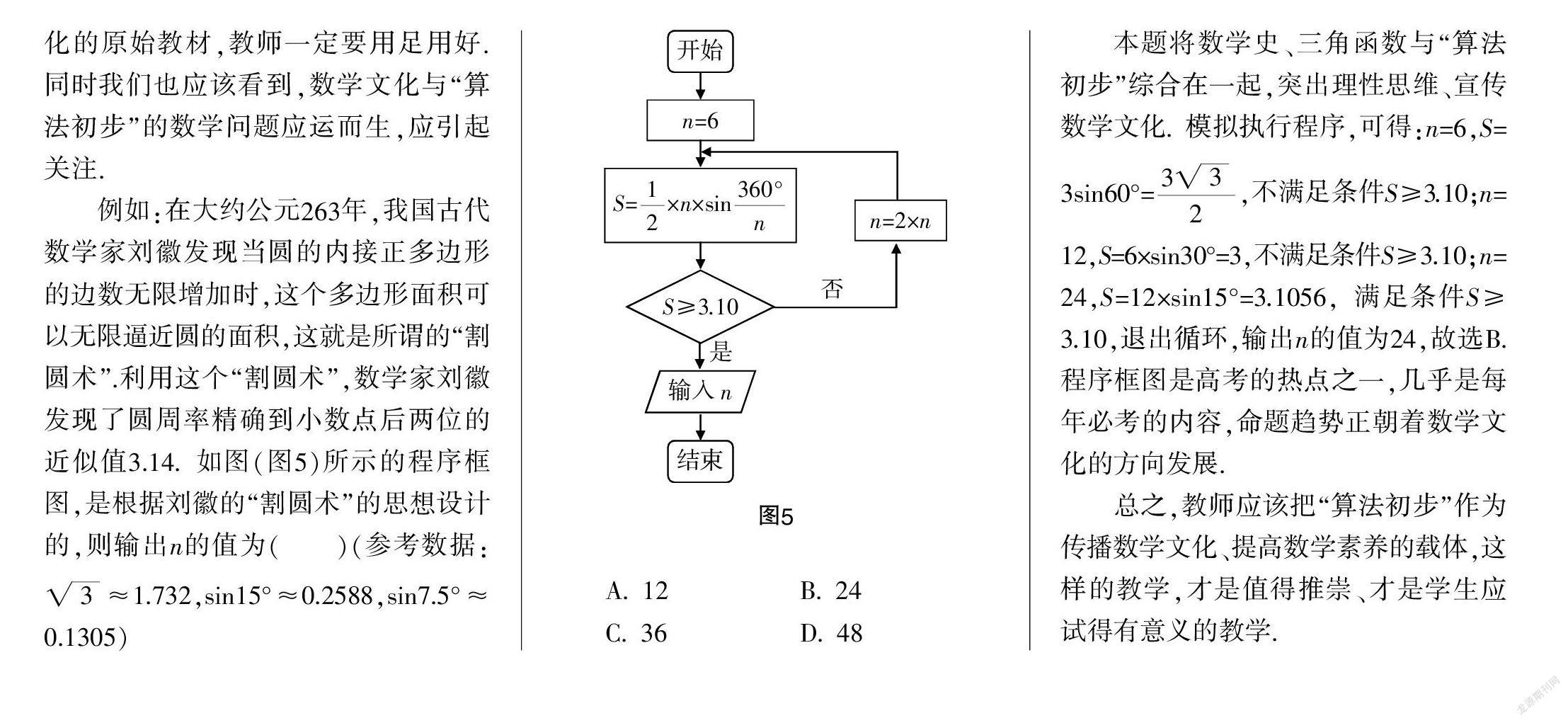
例如：在大约公元263年，我国古代数学家刘徽发现当圆的内接正多边形的边数无限增加时，这个多边形面积可以无限逼近圆的面积，这就是所谓的“割圆术”.利用这个“割圆术”，数学家刘徽发现了圆周率精确到小数点后两位的近似值3.14. 如图（图5）所示的程序框图，是根据刘徽的“割圆术”的思想设计的，则输出n的值为（  ）（参考数据：≈1.732，sin15°≈0.2588，sin7.5°≈0.1305）

A. 12  B. 24

C. 36  D. 48

本题将数学史、三角函数与“算法初步”综合在一起，突出理性思维、宣传数学文化. 模拟执行程序，可得：n=6，S=3sin60°=，不满足条件S≥3.10;n=12，S=6×sin30°=3，不满足条件S≥3.10;n=24，S=12×sin15°=3.1056，满足条件S≥3.10，退出循环，输出n的值为24，故选B. 程序框图是高考的热点之一，几乎是每年必考的内容，命题趋势正朝着数学文化的方向发展.

总之，教师应该把“算法初步”作為传播数学文化、提高数学素养的载体，这样的教学，才是值得推崇、才是学生应试得有意义的教学.