高中数学新教材中的数学文化研究

戴姗姗 朱哲

[摘  要] 基于数学文化的视野，从栏目分布、文化类型、运用水平以及文化功能对新人教A版高中数学必修教材“指数函数与对数函数”进行量化分析. 研究发现：数学文化类型分布不均衡，数学文化功能略显单一，等等. 建议数学教科书呈现多样数学文化类型、体现全面且高层次的文化功能等.

[关键词] 数学文化;高中数学;教材

把数学文化内容与高中数学各模块内容有机结合是高中数学课程明确提出的要求. 《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课标》）中提到：“教材应当把数学文化融入到学习内容中，可以适当地介绍数学和科学研究的成果，开拓学生的数学视野，激发学生的学习兴趣与好奇心，培养学生的科学精神.”[1]数学教材作为数学知识传播的重要媒介和重要工具，同时也是教师教学、学生学习数学的主要资源. 对数学教材中的数学文化进行解读，有利于教师对教材的深入掌握，有利于将数学教材中数学文化所蕴含的核心素养、数学方法深入传递给学生，同时能够培养学生学习数学的积极性与兴趣. 当数学文化真正渗透进数学教材，与数学课堂教学融为一体时，数学的魅力才能真正展现出来，数学就会显得生动有趣;数学教材通过文化层面对学生进行教学，能让学生更加专注数学、更加理解数学、更加热爱数学.

为此，文章以《普通高中教科书·数学（人教A版）》（第一册）的第四章“指数函数与对数函数”为例，从微观视角入手，探究“在什么地方渗透数学文化”“渗透了哪些数学文化”“怎样渗透数学文化”以及“数学文化有什么作用”等问题，对这一章节进行教材分析，以期对教材编写人员和教育教学工作者提供启示与建议.

[⇩] 教材分析理论框架

数学教材作为学生最初接触数学知识的重要工具，对学生具有高程度的影响力，而数学文化将教育的内容渗透进知识的学习过程中，又具有极大的教育价值，探究教材中数学文化的栏目分布、数学文化类型、数学文化运用水平、数学文化功能，能够有效考察教材中数学文化的分布情况.

1. 數学文化栏目的分布

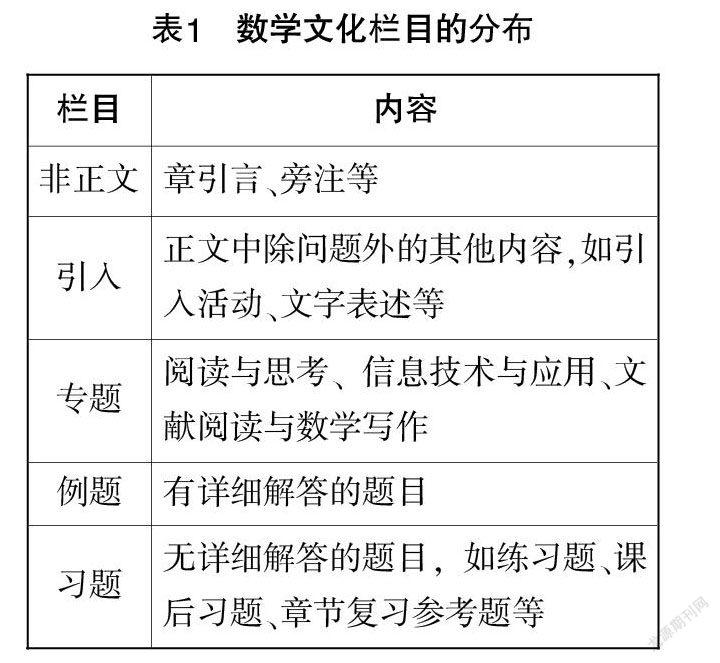
教材栏目设置丰富，包括章引言、引入、例题、旁注、阅读与思考、信息技术与应用、例题、练习题等. 各栏目中都分别渗透了数学文化，借鉴王建磐、汪晓勤、洪燕君的研究[2]，将各个类型相似的栏目进一步进行了整合处理，形成文章对教材中数学文化栏目分布的分析框架，将教材栏目分为非正文、引入、专题、例题、习题五类，具体分类见表1.

2. 数学文化类型

将数学文化与数学教材进行有机结合，通过文化层面让学生感受数学的魅力，首先必须明确数学文化的教学内容. 过去已有大量的学者对数学文化的类型进行了划分，汪晓勤为研究各国高中数学教材中的数学文化，将数学文化的类型界定为数学史、数学与生活、数学与科学、数学与人文、数学与艺术、趣味数学六类[3];王建磐等在比较中、法、美高中数学教材时将数学文化内容类型整合为数学史、数学与现实生活、数学与科学技术、数学与人文艺术等四类[2];唐恒钧、张维忠在研究澳大利亚数学统一评估试题中将数学文化类型分为数学史、数学与生活、数学与科技、数学与人文社会、数学游戏、数学与艺术体育等六类[4];章勤琼、张维忠将高中数学新教材中的数学文化类型分为体现科学价值的内容、体现应用价值的内容、体现人文价值的内容以及体现美学价值的内容[5].

文章基于上述对数学文化内涵的理解，将“指数函数与对数函数”中的数学文化类型分为数学史、数学与生活、数学与科技、数学与人文艺术等四类. 参照PISA相关分类，将数学文化类型细化，主要具体内容见表2.

3. 数学文化运用水平

数学文化是数学的灵魂所在. 为了全方面从数学文化角度研究数学教材，除了研究数学文化类型外，还需研究数学文化在教材中的运用水平高低，即数学文化与数学知识的关联水平. 文章借鉴王建磐所提出的框架，将数学史的运用水平由低到高划分为点缀式、附加式、复制式、顺应式四个层次;将其余类型的数学文化的运用水平分为两大类三小类：外在型和内在型（又细分为可分离型和不可分离型）[2].

4. 数学文化的功能

文章借鉴唐恒钧、张维忠等引用的Dickenson-Jones基于数学教材与文献的分析提出的观点，将数学文化的功能分为五类：提供背景性情境、提供应用性情境、拓展数学思维与方法、促进数学与文化交融、体验文化实践[6].

[⇩] 研究设计

1. 研究对象

将《普通高中教科书·数学（人教A版）》（第一册）的第四章“指数函数与对数函数”作为文章的分析对象. 该教材是浙江省2020年秋季学期开始全面实施使用的新教材，对其进行研究，有利于较为全面地了解当前数学文化在教材中的具体情况.

2. 研究方法

文章采用的研究方法是内容分析法. 内容分析法是指对教材内容进行客观、系统、量化分析的一种科学研究方法，文章通过选择、分类、统计三个步骤对数学文化元素进行定量分析.

3. 数据的收集与整理

在统计过程中，数据的收集与整理遵循以下操作标准实施：

（1）对教材中出现的不同的数学文化元素分别计数，同一个数学文化元素出现在教材不同地方也分别计数，如遗址中遗存物碳14出现在非正文栏目的章引言中，同时也出现在后面的例题中，均计数.

（2）当教材中某一处出现多种类型的数学文化时，取最能反映该处特点的分类. 例如，“函数的应用（二）”的例4，出现了良渚古城水坝数学文化元素，属于“数学与人文艺术”类型，同时也出现了碳14元素，属于“数学与科技”类型，考虑到该处试题偏向于碳14数学文化元素，因而被视为“数学与科技”类型.

[⇩] 研究结果与分析

两位研究者按照文章的研究框架，对“指数函数与对数函数”这一章节进行了数据分析，对比分析结果，对其中不一致的地方进行了探讨，最终达成了一致认识，并且通过数据对比，得到如下分析.

1. 数学文化栏目的分布

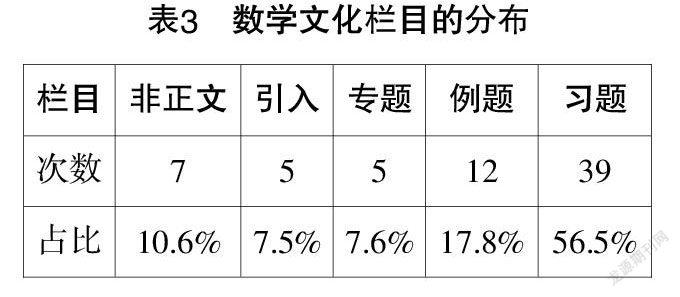
“指数函数与对数函数”这一章节共59页，数学文化内容丰富，多达69处，按照分析框架，对其进行分析，结果如表3所示. 数学文化在习题部分所占比重最大，高达39次，占比56.5%，当然这与习题在教材中所占比例较大有关，同时也与习题本身可容纳的数学文化背景有关. 在习题中渗透数学文化，可使习题生动形象，增添趣味性，让初次接触相关知识点的学生有亲切感. 其次是例题，占比17.8%，例题中的数学文化作为数学知识的背景素材，例题在教材中的篇幅也是可观的，当然这还与“函数”的学习目的有关联，意图让学生通过应用数学知识来解决实际问题，即函数的应用. 教材的其余栏目（非正文、引入、专题）篇幅相差不大，其数学文化数量也比较接近. 总体来说，“指数函数与对数函数”这一章节的数学文化数量与栏目篇幅的占比较为均衡.

2. 数学文化类型

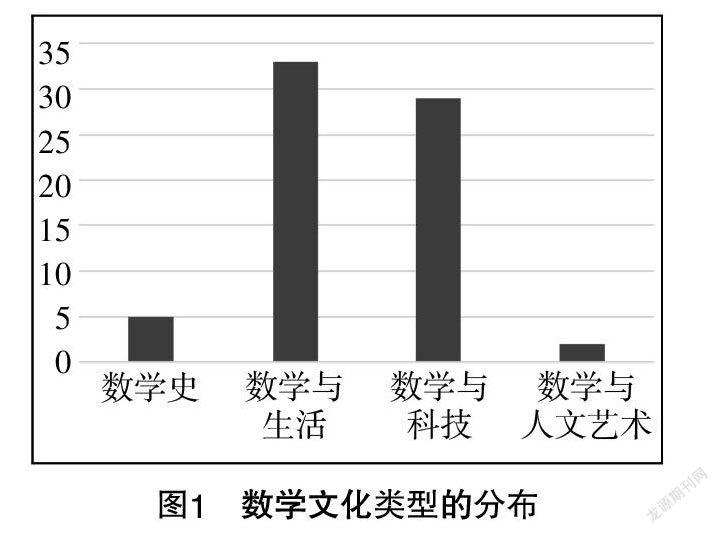
按照文章的分析框架，对四种数学文化类型出现的次数进行了统计，具体结果如图1所示.

统计分析后得到，四种数学文化类型的基数分别为数学史5道，数学与生活33道，数学与科技29道，数学与人文艺术2道. 数学与生活和数学与科技所占比重最大，分别占比47.8%和42.0%，两者相加所占比例高达89.8%，可见教材比较注重学生与生活和科技的联系，而其他数学文化类型的数量相对较少，数学史和数学与人文艺术仅占7.3%和2.9%.

（1）数学史

从题目数量来看，这一章节的数学文化涉及的数学史数量较少，并未落实将数学史融入教材的理念. 从教材中具体的史料内容来看，4处数学史介绍了数学概念、思想、方法的历史起源和发展背景，1处介绍了数学家经典语录. 例如，专题栏目的“阅读与思考”介绍了中外历史上的方程求解，展现了中外数学家探究方程求解的历程;介绍了对数的历史起源，由于社会生产和科学技术的需要，人们在大数的运算上有了更高的要求，苏格兰数学家纳皮尔结合运动学和几何学发明了对数. 专题栏目的“文献阅读与数学写作”引用了法国数学家拉普拉斯的经典语录：“因为省时省力，对数倍增了天文学家的寿命. ”教材落实了《课标》要求——“将数学史融入中小学的数学教学，有助于学生对数学概念和思想方法的理解”. 但是数学史内容类型单调，可以适当插入数学家生平介绍、数学历史名题等内容使学生体会到中外众多数学家在探索数学知识的艰辛历程和非凡的智慧，培养学生的探索精神.

（2）数学与生活

这一章节的数学文化涉及的数学与生活数量最多，教材在编写过程中充分挖掘了学生身边的日常生活、学校生活、社会生活、经济生活以及职业生活等所涉及的数学内容，充分体现了数学与生活的密切联系. 习题选材丰富，不仅体现了国民经济和社会发展、实时的社会热点问题，又考查了学生多方面的能力，如数学分析能力、阅读理解能力、数学建模能力等. 但是习题设置方面有部分习题没有与时俱进，如“函数的应用（一）”中的課后习题11，房价仍停留在2012年;还有部分习题真实性不够，不具有一定的实际意义，如“4.4 对数函数”中的例题2，设某地初始物价为单位1，该问题背景单一、枯燥，建议教材编拟时能够新颖创新.

（3）数学与科技

科技是第一生产力，而数学是其他学科的基础. 在这一章节，数学与科技的数量占比较大，可见教材充分重视数学与科技的力量. 教材中科技的选材内容丰富，在生命科学、地球科学、物质科学、高新技术领域均有涉及，如“对数函数”中的例4“溶液酸碱度的测量”，将化学知识与数学知识相结合，拓展了学生的知识层面，让学生感受到了数学与科技的紧密相连，同时旁注显示了人体中胃酸的含量，通过数学知识让学生计算胃酸的pH值，属于生命科学与数学的联系，增添了题目的趣味性.

（4）数学与人文艺术

“指数函数与对数函数”这一章节的人文艺术数量极少，仅含2道，说明数学与人文艺术的联系体现得不够紧密，有待加强. 将数学与人文艺术相结合能够改变学生对数学严谨刻板的印象，增添数学学习的兴趣，在人文、美术、音乐、建筑等方面含有大量的数学元素，挖掘数学知识背后蕴含的人文艺术素材，让学生感受到艺术与数学美的熏陶.

3. 数学文化的运用水平

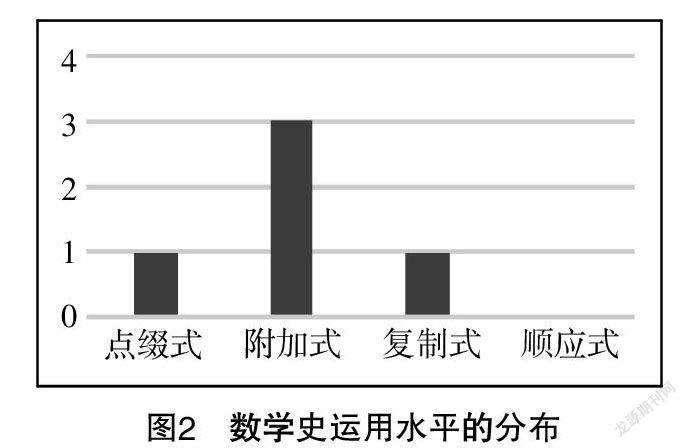
从图2可以看出，数学史运用水平的分布仅有三个层次——点缀式、附加式和复制式，对应的数学文化数量分别是1，3，1. 附加式是使用最多的一种方式，顺应式在这一章节没有体现. 对于数学史的运用方式多停留在中低水平，间接融入数学史的运用方式不足.

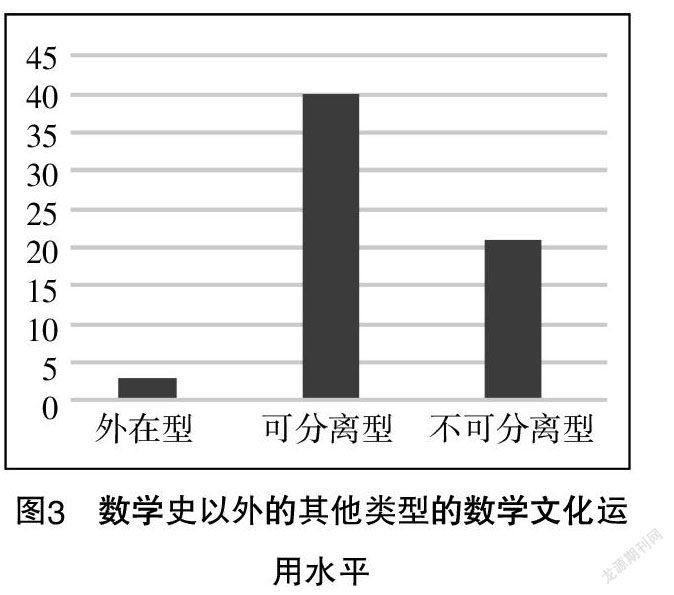
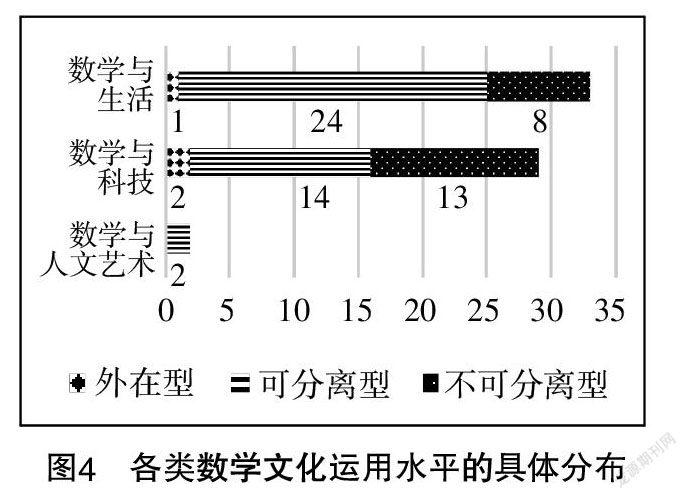
如图3所示，数学史以外的其他类型的数学文化运用水平则遍布全部层次，外在型、可分离型、不可分离型均有体现，对应的数量分别为3，40，21，占比分别是4.7%，62.5%，32.8%. 可分离型出现的次数最多，其次是不可分离型，其他类型的数学文化以中高水平为主，分布较合理. 进一步考察各类数学文化运用水平的状况，如图4所示，数学与生活和数学与科技的运用水平具有较高的层次性，分布较合理，而数学与人文艺术的运用水平集中在可分离型，也就是说人文艺术作为文化背景只是用来掩饰数学问题的，删去这个文化背景，也不会影响该问题的提出和解决，运用水平较低.

4. 数学文化的功能

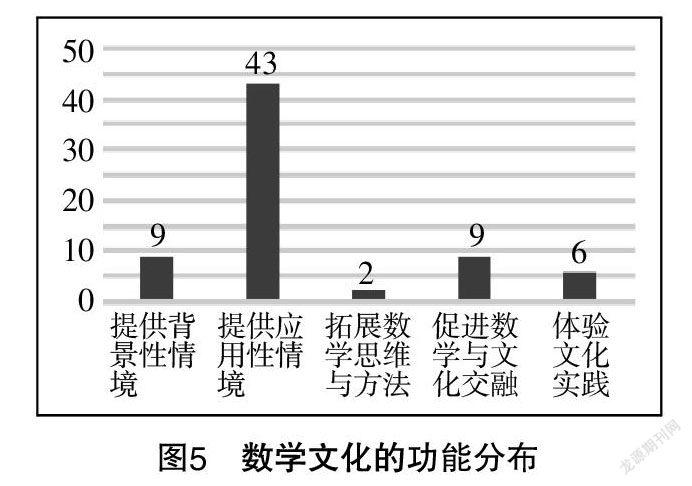
如图5所示，“指数函数与对数函数”这一章节中数学文化的五种功能均有呈现，其中，提供背景性情境出现了9次，提供应用性情境出现了43次，拓展数学思维与方法出现了2次，促进数学与文化交融出现了9次，体验文化实践出现了6次. 提供应用性情境在五个功能里一枝独秀，这与教材对数学应用的重视以及习题栏目篇幅有很大的关系.

[⇩] 研究结论与启示

基于《普通高中教科书·数学（人教A版）》（第一册）的第四章“指数函数与对数函数”中数学文化的栏目分布、类型、运用水平和功能的统计和分析，得出了以下结论：

其一，在数学文化栏目的分布上，数学文化主要集中在习题栏目，将近六成的数学文化均来自于此，当然这与习题栏目可纳入的文化元素的多寡以及栏目篇幅有关，但是各栏目数学文化的数量与各栏目在教材中篇幅的比例成正相关，较为均衡.

其二，数学文化类型的分布不均衡. 从数学文化的总量来看，数学与生活占比最大，可见“数学回归生活”的理念已渗透进了教材编写人员中;其次是数学与科技，教材与前沿科技的联系较紧密，两者总和占九成左右，此现象的出现与可纳入的文化素材的多寡、难易等有关联，也可能与这一章节中函数具有的与实际生活结合的应用性质有关. 但是数学史和数学与人文艺术的数学文化极少，有待改进. 从数学文化内容来看，部分數学文化内容的素材不够真实自然，还有部分习题选用的素材依旧停留在以前的年代，没有与时俱进.

其三，在数学文化的运用水平上，数学史的运用水平分布不均衡，主要集中在中低水平，教材主要以附加式为主，顺应式的运用水平没有出现. 其他类型数学文化的运用水平层次均有涉及，主要以中高水平为主，可分离型的运用水平占比最大，数学与生活和数学与科技的运用水平分布较合理，数学与人文艺术的运用水平分布还有待改进.

最后，数学文化的五种功能在教材中均有体现，提供应用性情境的数学文化呈现了一枝独秀的趋势，可见教材对数学应用的重视. 其他数学文化的功能就略显单一，有待深化.

数学教材是数学文化和数学知识点连接的重要通道，针对文章的研究结论，给出如下建议：

第一，在编写教材时，应注重在例题、习题栏目融入数学文化元素，让学生体会数学文化的魅力，锻炼学生的思维能力、实践能力，为初学新知识点的学生提供有意义的问题背景. 此外，还应尽量做到各栏目中数学文化的数量与栏目在教材中所占篇幅的比例均衡.

第二，在教材编写时，应适当增加数学史、数学与人文艺术等内容. 事实上，古今中外大量优秀的数学家以及他们浓缩的智慧结晶著作和名题都是很好的编写方向，在许多文化艺术作品中也蕴含着大量的数学元素，将其融入数学教材，可以增加学生的民族自豪感以及数学美的熏陶. 同时，数学文化背景材料的整合与编写应真实自然，可以增加一些学生易接触或对未来有帮助的文化素材;文化素材要与时俱进，可以增加一些时事热点. 教材在其他数学文化方面太过于强调知识与技能，对于情感态度的价值观方面的渗透不太突出，这一方面主要是通过数学史进行渗透的，建议教材在编写时挖掘其他数学文化上的情感态度的价值观.

第三，数学文化应体现更高层次的运用水平，教材编写应提倡以顺应式为主的数学史运用水平，倡导其他数学文化类型的不可分离型运用水平，使数学与文化成为有机统一的整体，体现数学的应用价值. 建议对于低层次的数学文化，教师在教授时可以适当进行改编. 例如，这一章节有一数学文化介绍了中外历史上的方程求解历程，该内容放在了“阅读与思考”栏目中，内容靠后且篇幅较长，教师往往会让学生课后阅读或者教师直接过而不讲. 对于这种低层次的数学文化，建议教师对该数学文化加以改编，搜索历史上方程求解的详细历程，将其融入方程的根与函数的零点等相关内容，将过去数学家在方程求解过程中的疑惑问题设置成课堂悬念，从而让学生感受到数学的乐趣与魅力，而不是以往枯燥乏味的感受.

最后，教材编写时，要体现更加全面且高层次的文化功能，提倡拓展数学思维与方法，促进数学与文化交融和体验文化实践的条目. 学习数学不仅是为了解决问题，更是为了培养学生的数学意识和思维，以及创造能力和实践能力.

总之，从数学文化的视角来看，《普通高中教科书·数学（人教A版）》（第一册）的第四章“指数函数与对数函数”还存在一些有待完善的地方，但总体上展现了多样的数学文化类型，除数学史和数学与人文艺术外的数学文化有着较高的运用水平，并体现了全面的文化功能. 当然，这仅是以教材一个章节内容展开的试验性研究，教材其他章节是否存在类似的特点，尚需要做进一步的考察.

参考文献：

[1]  中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）[M]. 北京：人民教育出版社，2020.

[2]  王建磐，汪晓勤，洪燕君. 中、法、美高中数学教科书中的数学文化比较研究[J].教育发展研究，2015，35（20）：28-32+55.

[3]  汪晓勤. 主要国家高中数学教材中的数学文化[J]. 中学数学月刊，2011（05）：50.

[4]  唐恒钧，张维忠. 澳大利亚数学统一评估试题中的文化研究[J]. 数学通报，2016，55（03）：7-11.

[5]  章勤琼，张维忠. 高中数学新教材中的数学文化[J]. 中学数学教学参考，2006（21）：1-3.

[6]  唐恒钧，张维忠，李建标，佘伟忠. 澳大利亚数学教材中的数学文化研究——以“整数”一章为例[J]. 数学教育学报，2016，25（06）：42-45.