基于几类机器学习模型的房价预测分析
2022-06-08周亮锦赵明扬
周亮锦 赵明扬
(1.韩山师范学院经济与管理学院金融大数据中心,广东 潮州 521000;2.韩山师范学院数学与统计学院,广东 潮州 521000)
一、前言
房地产业是影响我国经济发展的重要因素,尤其在2003年国务院18号文件正式确立房地产业为国民经济支柱产业的地位之后。随着房地产业的快速发展,我国的房价在过去的二十年间经历了多次较大幅度的持续上涨,甚至陷入“越调越长”的怪圈,直到被称为史上最严楼市调控的北京“3·17”调控政策的出台。以此为契机,“因城施策”“一城一策”等以“稳房价、稳地价、稳预期”为目标,以“坚持房子是用来住的,不是用来炒的”为定位的房价调控政策成为各地房地产市场的关键词。再加上2020年以来全球范围内新型冠状病毒肺炎的暴发,以及楼市“三道红线”的出台,房地产市场正遭受多元化冲击,由此带来的民生问题、社会问题和经济发展问题引发人们对房地产市场,尤其是房价的广泛关注。
围绕房价相关问题,学术界、政府和实际工作者展开了深入探究。归纳起来,这些研究主要集中在房价泡沫、房价影响因素和房价预测三个方面。其中:对房地产泡沫问题的研究主要涉及对泡沫是否存在的讨论、对泡沫化程度的度量和对泡沫化成因的探究;对房价影响因素的研究涉及对各相关因素,如供求因素、消费者个体因素、住宅特征和宏观调控政策等对房价的影响;对房价预测的研究则主要体现宏观经济(Crawford等,2003;胡六星等,2010;高玉明等,2014;黄明宇等,2019)和住宅特征两个视角(Bin,2004;Selim,2009;李恒凯等,2012;孙逸等,2020)。
近年来,随着国外内关于房价预测研究的日趋成熟,很多学者都将研究重点放在了预测模型的对比、优化和修正上(Bork,2015;Wei,2017;李宝强等,2017)。同时,随着互联网和大数据研究的蓬勃发展,基于大数据方法的相关模型,如支持向量机模型、BP神经网络、随机森林和K邻近模型等(Plakandaras等,2015;江源,2019;王葛成,2020)也被引入到房价预测中来。本文使用K近邻法、支持向量机、决策树和随机森林这几类机器学习算法建立房价预测模型,该研究将从理论和方法上丰富和完善房价预测问题的研究体系。通过该研究,以期有助于政策制定者了解房价的发展走势,继而为政府的宏观调控提供更好的参考,同时也为房地产开发商、购房者作出更好的投资决策提供借鉴,促进房地产市场的平稳健康有序发展。
作为人工智能领域发展最快的分支之一,机器学习在各个领域已得到广泛的应用(周志华,2016;王宇韬等,2020;韩宝国等,2018;黄文等,2014)。本文主要借助于机器学习库scikit-learn来实现的相应的算法。scikit-learn发布于2017年,它提供了分类、回归、降维和聚类等机器学习算法(华校专等,2017;Gavin,2017)。
二、数据来源
房价的波动在本质上依赖于市场上供求关系的变化,但也受到国家宏观政策、城市发展等宏观环境的影响。借鉴已有相关研究,本文在实证分析部分选取的指标主要包括需求、供给及宏观环境三类。
就需求而言,人口数量的增加、收入水平的增长以及住宅销售面积的增加在一定程度上能推动房价的上涨。其中,代表人口数量的指标有年末人口数量,常住人口数量。代表收入的指标有人均可支配收入、人均消费支出、在岗职工平均工资和年末储蓄余额。
就供给而言,房价波动主要受到土地价格、建造成本、住宅开发投资额、土地购置面积和住宅竣工面积的影响。土地价格、建造成本作为成本能推动房价的上涨,而在需求不足的情况下,房地产开发住宅投资额、土地购置面积和住宅竣工面积的增加会对房价产生负向影响。
就宏观环境而言,主要是城市发展以及国家宏观政策。其中,代表城市发展的指标有经济发展水平GDP、人均GDP和物价水平CPI,而代表国家宏观政策的因素有利率、信贷和货币供应量。考虑到我国土地国有的特殊国情,房价的波动还受到地方政府土地财政的影响,相应的代表性指标有财政缺口和土地财政依赖。各指标的简要说明如表1所示。
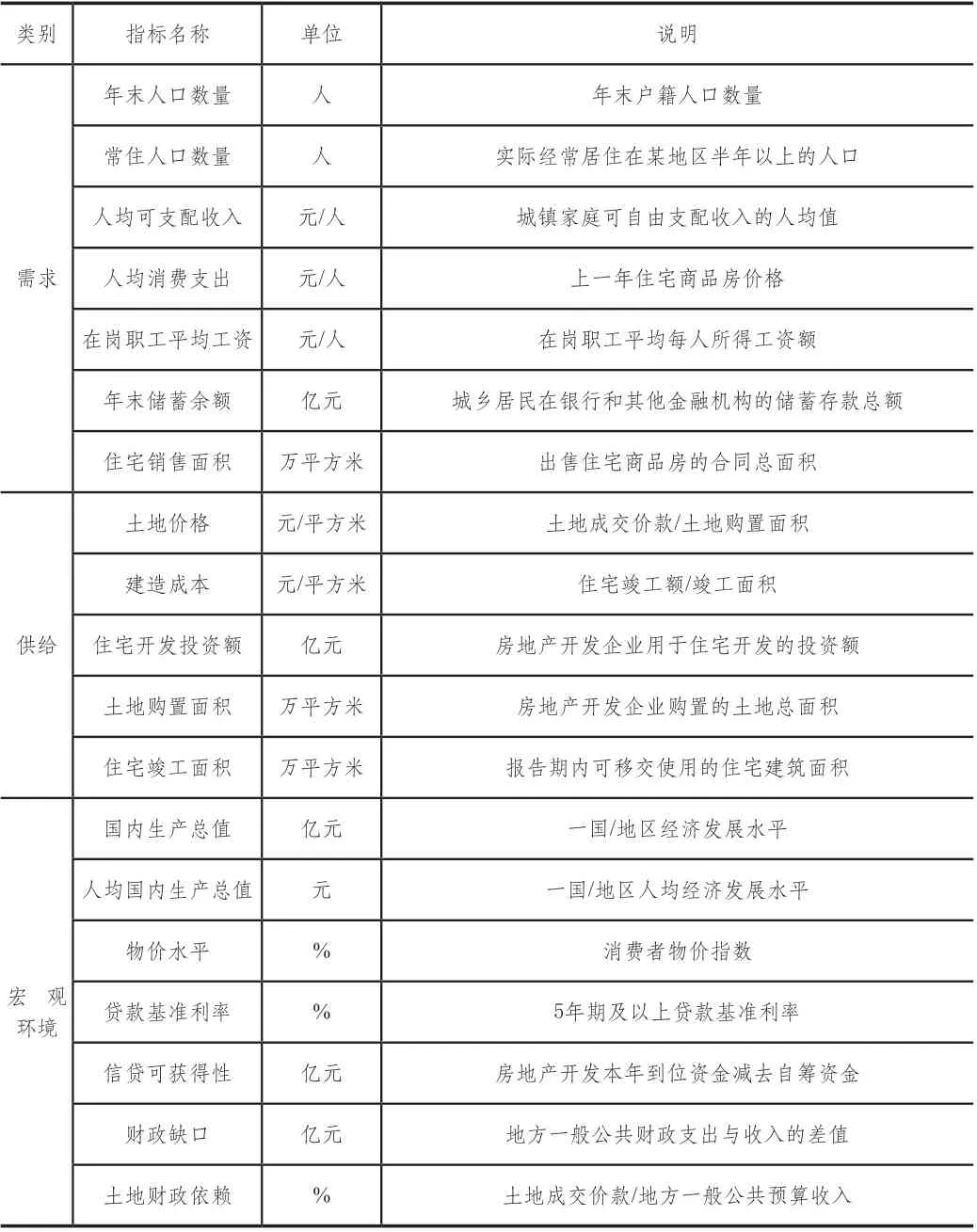
表1 指标名称及相应说明
鉴于数据的可获得性,本文选取1999年~2019年我国35个大中城市为考察对象。其中,住宅商品房的销售额和销售面积、住宅商品房的竣工价值和竣工面积、当期房地产开发企业到位资金和自筹资金、当期住宅商品房开发投资额和土地购置面积的相关数据来自《中国房地产统计年鉴》(1999年~2020年)。年末人口数量、常住人口数量、城镇家庭人均可支配收入、人均消费支出、在岗职工平均工资、国内生产总值、人均国内生产总值和地方一般公共预算收入/支出的数据来自各城市《城市统计年鉴》(1999年~2020年)。土地价格的数据来自中国地价监测网,国有建设用地土地成交价款的数据来自《中国国土资源统计年鉴》(2000年~2018年),5年期及以上贷款基准利率和物价水平的数据来自《中国统计年鉴》(1999年~2020年);缺失数据采用Lagrange插值法插入。为消除通货膨胀的影响,所有价格均经各城市CPI平减,住宅开发投资和信贷数据则经各城市固定资产价格指数平减,平减后的数据以1998年为基期。
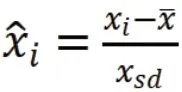
三、模型构建与结果分析
在机器学习中,通常把学习器的实际预测输出与样本的真实输出之间的差异称为“误差”,把模型在训练集上的误差称为“经验误差”,在新样本上的误差称为“泛化误差”。学习器的泛化误差越小,模型的预测精度越高。但新样本是未知的,且模型的泛化误差也无法直接获得。因此,我们通常采取的策略就是将得到的数据拆分为训练数据集和测试数据集,在训练数据集上进行模型的训练,然后以测试集上的“测试误差”对模型的泛化误差进行估计,继而选择泛化误差最小的模型。常用的数据拆分方法有留出法、交叉验证法、留一法等。这里采用的是留出法。数据拆分使用模块sklearn.model_selection中的train_test_split()函数来实现,参数test_size的值设置为0.25,即随机选取数据的1/4作为测试集,剩余的3/4作为训练集。为方便各机器学习模型之间的性能比较,需保证每次使用的训练集和测试集都是相同的,借助于tram_test_split()函数中的参数random_state来实现。
机器学习的各个模型都带有一些参数,如决策树中的深度参数,K近邻法中的K值选择,随机森林中决策树的个数等。通常情况下,使用模型的默认参数设置即可获得较好的结果和预测准确度。但如果要获得更为精确的结果,就需要对模型的这些参数进行调整,以寻求在给定数据集下的最优参数。对于该参数寻求过程,通常使用交叉验证和GridSearch来实现。在下面的模型训练过程中,设置K折交叉验证的划分份数为5。
1.K近邻法
K近邻法最早由Cover和Hart于1968年提出,是一种基本的分类和回归算法。其作为回归算法的基本原理是通过计算新数据与训练数据对应特征之间的距离,选取距离最近的K个样本的样本输出值的平均数作为预测值。在K近邻算法中,K值的选择对预测效果有较大影响。若K值过小,则整体模型变复杂,易造成数据的过拟合;若K值过大,则整体模型变简单,易发生预测错误。除了K值这一重要影响因素外,计算距离的方式也对结果有较大的影响。在K近邻法中,距离的计算有欧式距离和加权欧式距离两种方式。使用欧式距离时,距离近的点和距离远的点对结果的影响是相同的,这明显与实际不符。对于现实中的房价,当影响房价的各个因素比较接近,相应地区的房价也会趋向一致;而当各因素相差较大时,房价相应也会呈现出较大的差异。基于这样的事实,加权欧式距离的结果在理论上应优于欧式距离的结果。K近邻法借助于sklearn的子模块neighbors实现。K近邻法借助于sklearn的子模块neighbors实现。在网格参数寻优时,距离计算的方式分别设置为欧式距离和加权欧式距离,K值取{i∈,1≤i≤10}。模型训练结果表明,当使用加权欧式距离且K值为3时,效果最优,与实际相符。进一步地,为了更清晰地观察使用加权欧式距离时,K值的选择对最终结果的影响。这里以参数K为横坐标,以训练集和测试集上的拟合度(R2)为纵坐标绘制K值与R2之间的折线图(如图1所示),以探究K值对模型预测效果的影响。
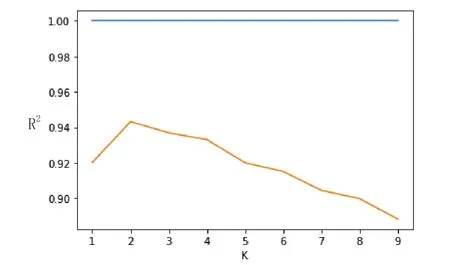
图1 加权欧式距离下K值与R2之间的关系
根据图1,可以发现参数K的最优值为3,这与GridSearch寻求的最优值是相符的。此时在训练集上的为1.0000,在测试集上的R2为0.9571。
2.支持向量机模型
支持向量机模型是一种建立在统计学习理论的VC维(Vapnik-Chervonenkis dimension)理论和结构风险最小化原则上的预测模型。它可通过非线性变换将输入变量映射到高维特征空间,即便在有限样本情况下,仍能在求解问题时以较好的泛化能力得到较小的误差。对于支持向量机而言,核函数(用于实现非线性变换)的选取至关重要。这里,我们分别选取多项式核、高斯核和Sigmoid核进行模型的训练和测试。其中多项式核的表达式为
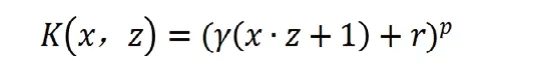
γ,ρ,r为参数。高斯核函数的表达式为:
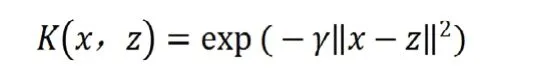
γ为参数。Sigmoid核的表达式为
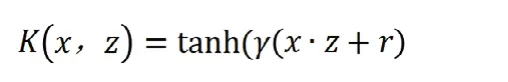
γ,r为参数。
支持向量机借助于sklearn的子模块SVM来实现。网格参数寻优结果表明,当使用多项式核,参数设置为γ=1,ρ=1,r=5时,效果最优,此时该参数组合在训练集上的拟合度(R2)为0.8939,而在测试集上的拟合度(R2)为0.9177。为了更清晰地观察各个参数对最终结果的影响,将其中两个参数固定为最优值,绘制剩余的那个参数(横坐标)和拟合度(R2)(纵坐标)之间的折线图(如图2、图3所示),以探究不同参数对模型结果的影响。
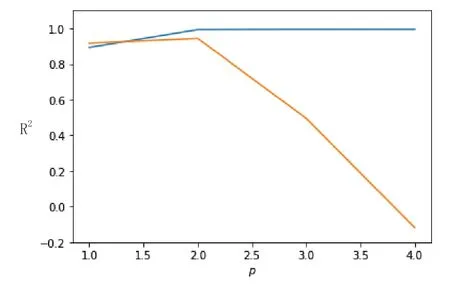
图2 参数p与R2之间的关系
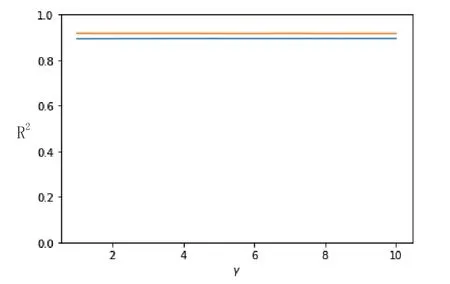
图3 参数与R2之间的关系
从图4可以发现,其结果与网格搜索的参数最优值是相符的。
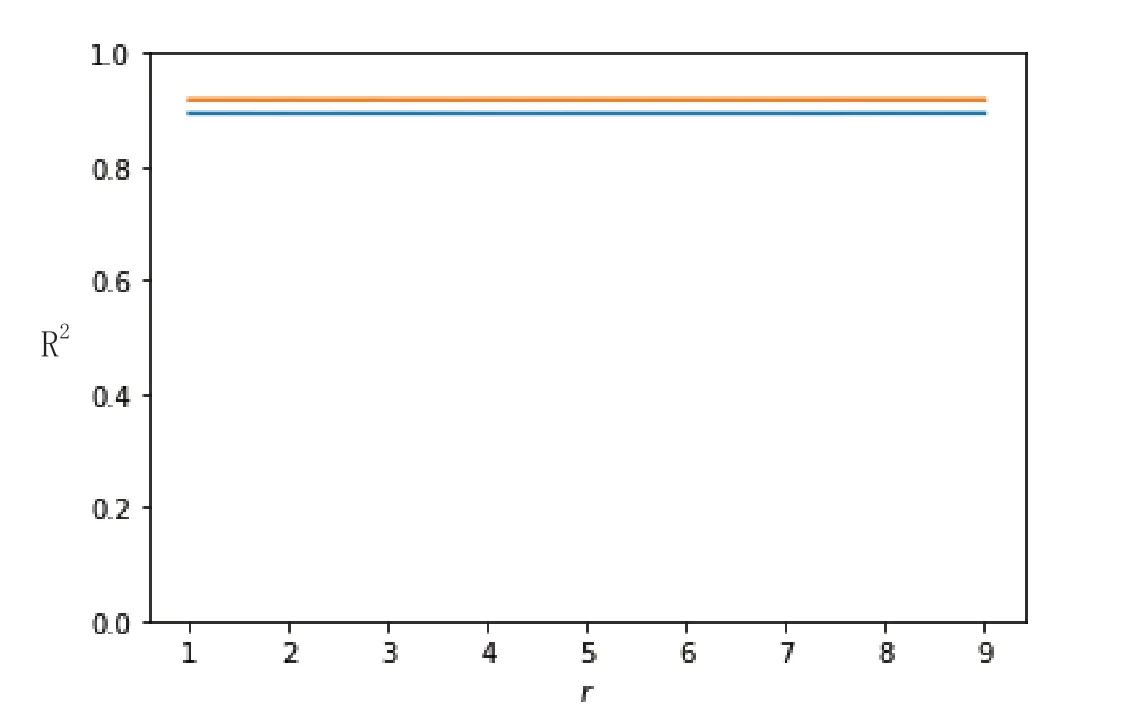
图4 参数与R2之间的关系
3.决策树模型
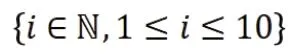
根据图5,可以发现决策树深度的最优值为4。此时在训练集上的拟合度(R2)为0.9470,在测试集上的拟合度(R2)为0.9007。
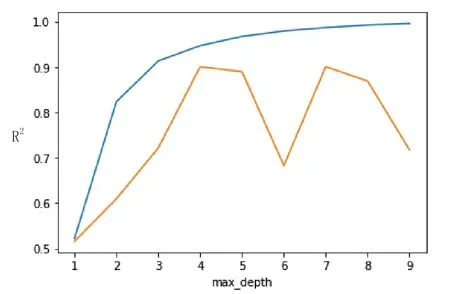
图5 决策树深度与R2之间的关系
4.随机森林
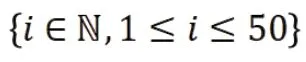
从图6、图7、图8可以发现,其结果与网格搜索的参数最优值是相符的。
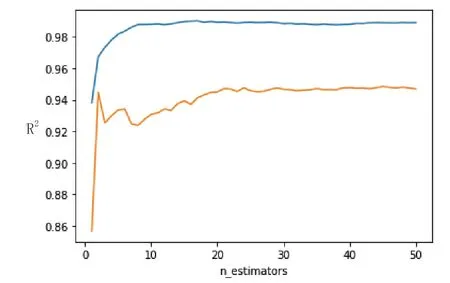
图6 决策树数目与R2之间的关系
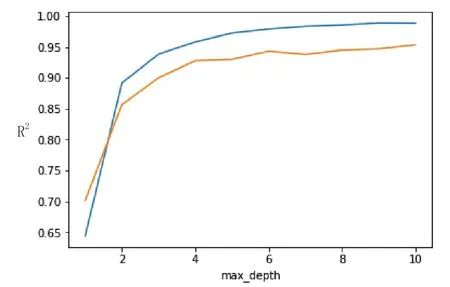
图7 决策树深度与R2之间的关系
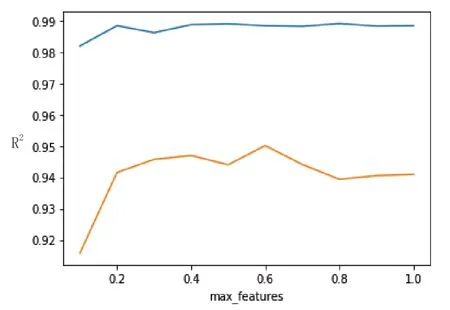
图8 特征选择比例与R2之间的关系
四、结论与讨论
综上,本文分别使用K近邻法、决策树、随机森林和支持向量机对1998年~2019年全国35个大中城市房价及其影响因素的数据集进行了房价预测模型的构建与测试。借助于K折交叉验证和GridSearch参数寻优,得到各模型的最优参数组合,如表2所示。
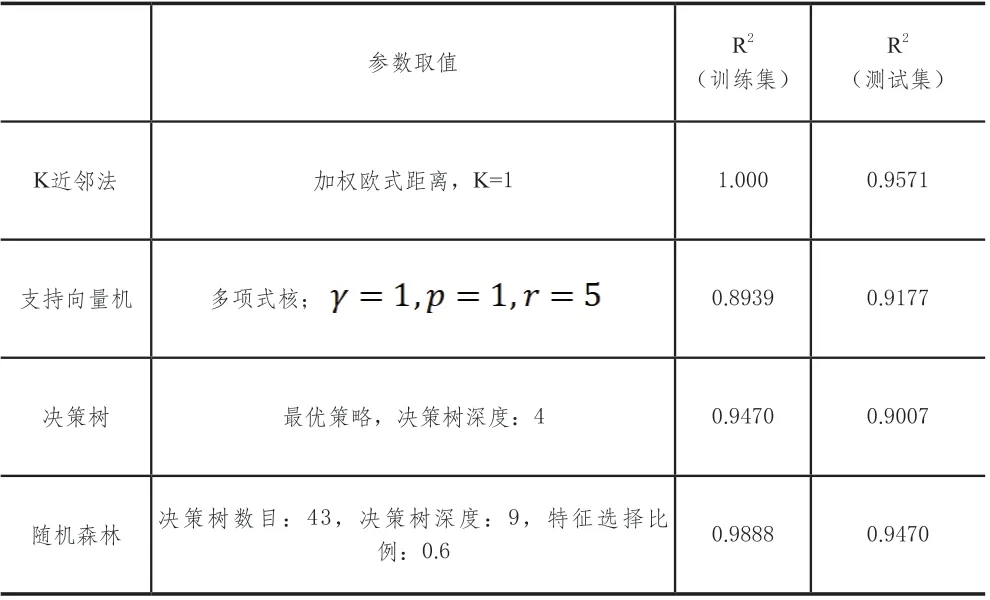
表2 各模型的最优参数组合
结果表明,从R2(测试集)的角度来看,最优参数组合中K近邻法>随机森林>支持向量机>决策树。但从理论上可知,K近邻法严重依赖于训练数据集,无法从模型本质上寻求房价影响因素与房价之间的数量关系,所以从理论角度来看,随机森林应是这4类模型中的最优模型。
尽管我们已经取得了一些有价值的结论,但仍有很多问题有待解决,例如利用数据降维降低影响因素的维数,通过引入其他机器学习方法(如XGBoost,CNN等)并结合GridSearch等技术提高模型的精度,以期构建稳健性更好、精度更高的房价预测模型。
