供油孔区域惯性效应对液体静压推力轴承承载力的影响
2022-06-07田助新
田助新
(1.三峡大学 机械与动力学院,湖北 宜昌 443002;2.华中科技大学 机械科学与工程学院,武汉 430074)
静压轴承的工作原理是通过流体压力将机械设备中的转动部件与支承件隔开,以减少转动副在运动中产生的摩擦。按照工作介质不同,静压轴承分为气体静压轴承和液体静压轴承,气体静压轴承主要用于轻载的精密机械仪器[1],而液体静压轴承由于油膜刚度大,吸振性好和启动功率低等优点,在车床、磨床等承载力大且载荷剧烈波动的机床中得到了广泛应用[2-3]。近年来,随着液体静压技术的发展,国内外已将静压轴承应用于军事装备、航空航天以及核工业等国家战略领域[4]。
文献[5]提出在分析液体静压推力轴承性能时需要考虑惯性效应,并给出了相应的理论推导;文献[6]设计了相关试验并开展了验证,提出的考虑油膜惯性效应的液体静压推力轴承静态特性分析方法基本成为后续研究液体静压推力轴承静态特性的标准方法;但文献[5]与文献[6]结果差异较大,文献[6]认为是由于热效应。
笔者通过分析发现,文献[6]试验中采用的液体静压推力轴承直径较小,供油孔半径与轴承半径之比为0.05的情况下,不能将供油孔当成一点处理,有必要考虑润滑油在供油孔区域的惯性效应。因此,本文在考虑供油孔区域惯性效应的基础上探讨了液体静压推力轴承供油孔区域惯性效应对其承载力的影响,分析了考虑供油孔区域惯性效应与不考虑供油孔区域惯性效应下承载力之间的相对误差。
1 理论推导
2种结构的液体静压推力轴承如图1所示,r为径向坐标,z为轴向坐标,r0为供油孔半径,r1为油腔半径,h为油膜厚度,βh为油腔油膜厚度,β为油膜厚度比(油腔区域油膜厚度与封油边区域油膜厚度的比值),R为轴承半径,ω为轴承转速,ps为供油压力。
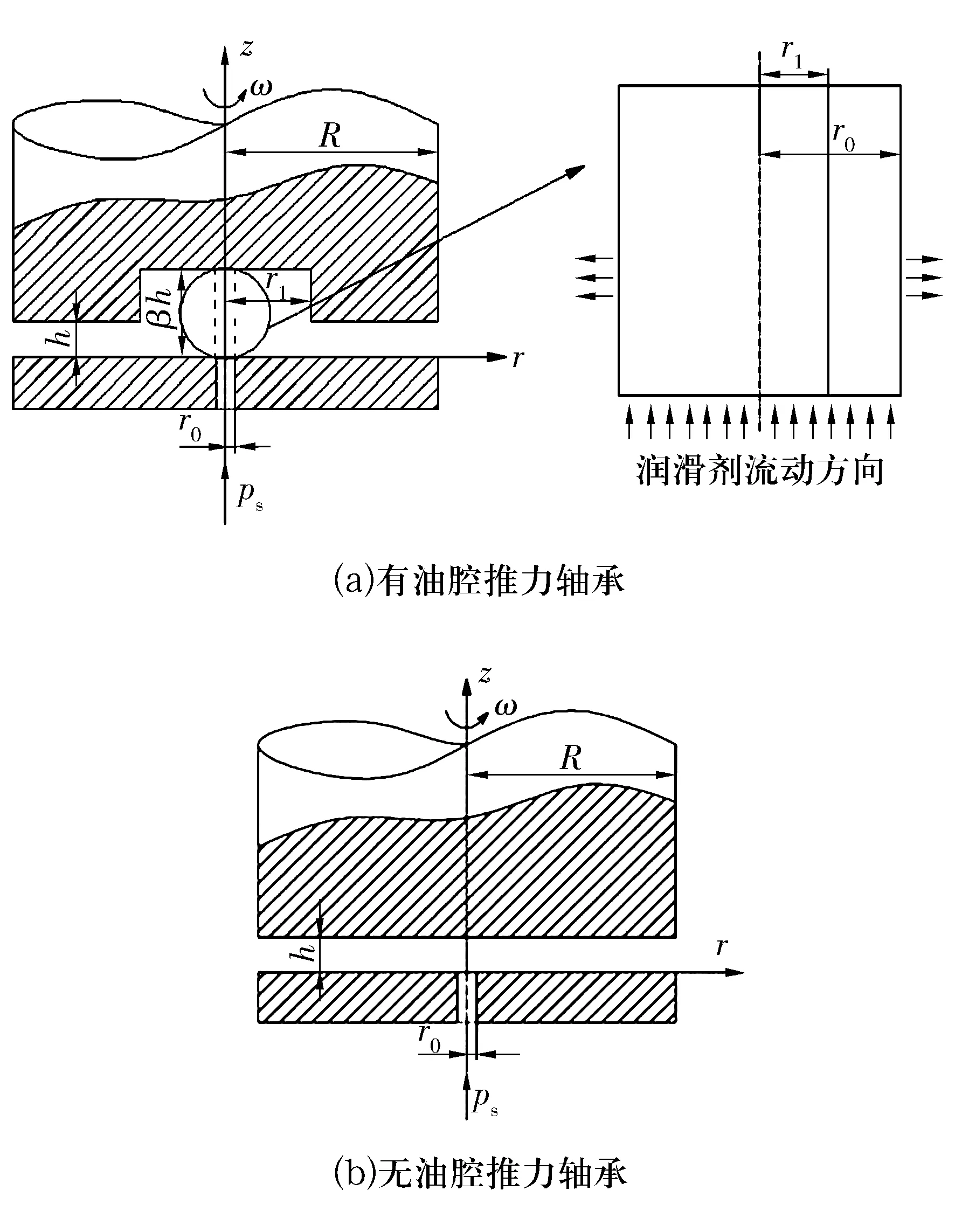
图1 液体静压推力轴承的结构
1.1 基本公式推导
不考虑润滑剂的非牛顿性和体积力,在极坐标下液体静压推力轴承油膜的纳维-斯托克斯公式可简化为
(1)
(2)
(3)
式中:ρ为润滑剂密度;v为润滑剂沿圆周方向的速度;p为润滑剂压力;μ为润滑剂黏度;u为润滑剂沿半径方向的速度。
(2)式应用边界条件是v|z=0=0,v|z=βh=rω,则圆周方向的流体速度分布为
(4)
将(4)式代入(1)式,运用边界条件u|z=0,βh=0,可得到流体沿径向的速度分布为
(5)
在z方向上从0到βh积分,可得到流量Q为
(6)
为简化计算过程,引入量纲一的量,即
则可得到量纲一的流量为
(7)
半径方向上油膜的量纲一的压力分布为
(8)
式中:S为轴承惯性参数;W为油膜承载力。
1.2 有油腔液体静压推力轴承承载力
1.2.1 供油孔区域油膜压力分布
(9)
式中:k为比例系数。
在供油孔区域,(8)式中的压力分布变为
(10)
(11)
将(11)式代入(9)式可求得比例系数k,进而得到供油孔区域的流量为
(12)
将(12)式代入(10)式,可得到供油孔区域的压力分布为
(13)
(14)
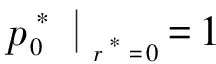
1.2.2 其他区域油膜压力分布
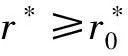
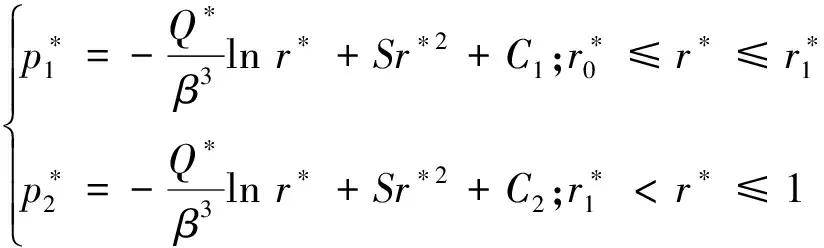
(15)
积分常数C1,C2和流量Q*可以通过边界条件
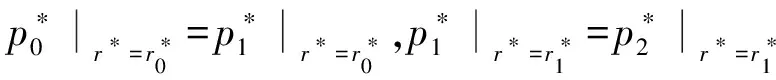
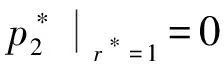
(16)
C2=-S,
(17)
(18)
1.2.3 轴承承载力
从(18)式可以看出,一旦液体静压推力轴承结构确定,总流量是一个常数,由此可得到轴承的压力分布为
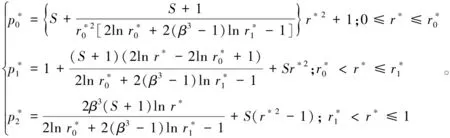
(19)
对压力进行积分得到液体静压推力轴承油膜的承载力为
W*=
(20)
1.3 无油腔液体静压推力轴承压力分布
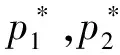
(21)
2 结果与讨论
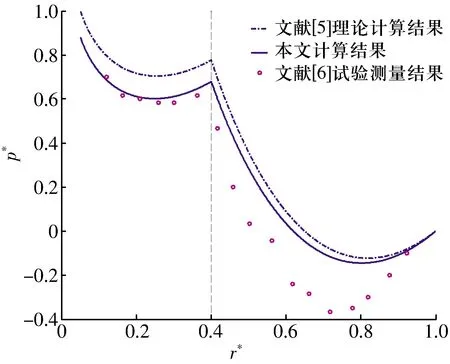
图2 有油腔液体静压推力轴承压力分布对比
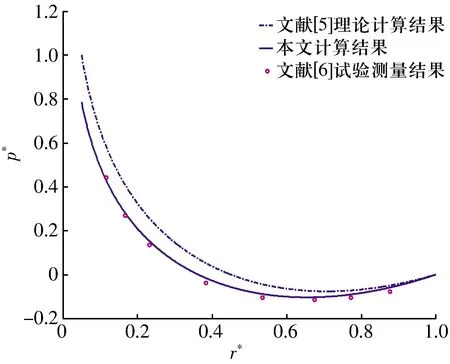
图3 无油腔液体静压推力轴承压力分布对比
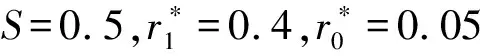
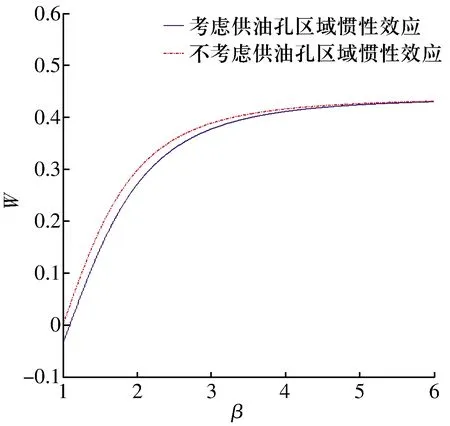
图4 液体静压推力轴承承载力与油膜厚度比的关系
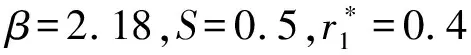
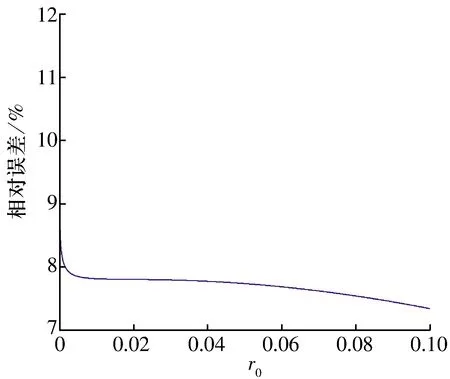
图5 供油孔半径对液体静压推力轴承承载力相对误差的影响
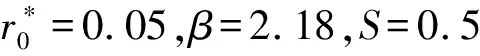
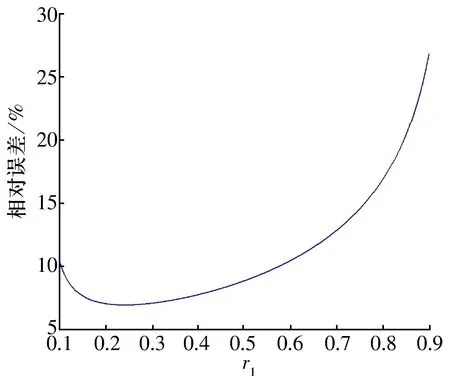
图6 油腔半径对液体静压推力轴承承载力相对误差的影响
3 结束语
讨论了油膜在供油孔区域的惯性效应对液体静压推力轴承静态特性的影响,并通过与已有文献中的理论计算和试验结果对比,说明了本文计算分析的正确性。供油孔区域的惯性效应对浅油腔液体静压推力轴承承载力的影响较明显,以浅油腔液体静压推力轴承为研究对象,探讨了轴承承载力在考虑和不考虑供油孔惯性效应之间的相对误差,供油孔半径和油腔半径均会影响这两者的相对误差,其中油腔半径对相对误差的影响比较明显,当供油孔半径大于0.002时,供油孔半径的变化对相对误差的影响幅度不超过1%。对于浅油腔液体静压推力轴承,相对误差基本在7%以上,因此,在分析浅油腔液体静压推力轴承静态特性时,需要考虑供油孔区域的惯性效应。
