变工况运行中结构参数对螺旋槽动压推力气体轴承承载力的影响
2022-06-07李云龙董志强
李云龙,董志强
(太原科技大学 机械工程学院,太原 030024)
螺旋槽动压推力气体轴承的表面刻有微米级的沟槽,按沟槽形式分为泵入型、泵出型和人字槽型,因其具有较高的承载力和较好的稳定性,在高速旋转机械和仪器中,特别是在航空航天仪器中得到了较广泛的应用,如惯性导航陀螺仪、低温透平膨胀机等[1-3]。螺旋槽动压气体轴承理论计算的发展初期是由纳维-斯托克斯(N-S)方程推导而成,经一系列的简化成为压缩性流体的非定常雷诺方程,从而求出近似解。文献[4]用 Whippler的窄槽理论研究了等间距排列的平行槽与平行板之间的流动,结果表明该理论适用于低转速的轴承;文献[5]提出的准不可压缩窄槽理论可应用于各种形状轴承的研究,但假定仍有不合理的地方使计算值误差较大;文献[6]提出了变函数保角变换理论方法,重点考虑了槽端部的影响;文献[7]采用差分法在变换坐标系后进行了润滑方程的计算;文献[8]采用有限元法对控制方程进行求解,得到了槽端半径比、螺旋角、气膜厚度比、槽数等对气膜承载力的影响;文献[9]用伽辽金方法对控制方程进行了变换,采用有限元法计算得到了压力分布;文献[10]采用有限体积法得到了气体轴承的离散方程,研究了轴承结构参数对承载力和摩擦力矩的影响,证明了有限体积法的可行性。
关于采用不同结构来改进轴承性能,国内外外学者做了大量的研究,分析了矩形槽、T形槽等螺旋槽槽形对轴承性能的影响。但大多通过求解雷诺方程分析空气轴承的性能而并未直接从N-S方程入手,不断尝试改进螺旋槽型、结构尺寸等参数都是为了改进轴承性能,增大轴承承载力,但较为全面地对轴承气膜承载力进行专门研究的探索较少。
为进一步从N-S方程了解多方面参数对轴承气膜承载力的影响,本文采用有限体积法并应用ANSYS—CFD(计算流体力学)软件对泵入型螺旋槽动压推力气体轴承进行数值模拟,分析特定工况下的端面流动状态,并在多种转速下对比分析不同槽数、螺旋角、槽深、台区轴承间隙、槽内径比、槽宽比和不同槽底结构以及泵入型、泵出型轴承结构对轴承气膜承载力的影响。
1 理论模型与计算方程
1.1 结构与理论
螺旋槽动压推力气体轴承结构如图1所示,轴承分为槽区、台区及密封区,轴承外圈半径为re,内圈半径为ri,螺旋线的基圆半径为rg,设台区轴承间隙为h1,螺旋槽深h2,则气膜总间隙h=h1+

图1 螺旋槽动压推力气体轴承的结构
h2,轴承外周圆上台区脊宽为b1,螺旋槽宽为b2,槽宽比γ=b1/b2,槽内径比λ=(re-rg)/(re-ri)。通常情况下螺旋线采用对数螺旋线形式,其极坐标为
r=rgeθtan α,
(1)
式中:r为螺旋槽的极半径;θ为角度坐标;α为螺旋角。
选取的轴承模型有12对槽台,由于轴承端面几何模型符合周期性分布和中心分布原则,所以气膜层分布同样符合周期性原则,为节省计算时间,提高计算效率,选取计算区域的1/12(端面1个槽台区和相连的密封坝区)建模,如图2所示。由于气膜厚度是微米级,气膜总间隙一般为几十微米左右[11],将气膜导入ICEM网格划分软件中进行网格划分难度非常大,所以对气膜在厚度上放大100倍,以便于观察及网格划分,进行流体模拟仿真时,在FLUENT软件中恢复原尺寸。
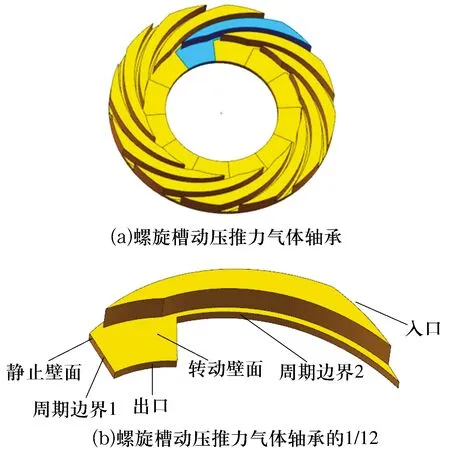
图2 螺旋槽动压推力气体轴承的三维模型
强制性边界条件为
(2)
式中:p为气体压力;pin进口压力;pout为出口压力。
周期性边界条件为
p(r,θ)=p(r,θ+2π/Ng),
(3)
式中:Ng为螺旋槽数。
1.2 理论假设
基于N-S方程的质量守恒定律、动量守恒定律、能量守恒定律并考虑螺旋槽动压推力气体轴承自身结构特性,做如下假设:
1)忽略气体的体积力和惯性力;
2)气体分子在界面牢固吸附,无滑移;
3)忽略重力产生的影响;
4)气膜流场分析采用稳态定常;
5)忽略壁面粗糙度的影响;
6)轴承与推力板严格对中,忽略工作中系统扰动、偏摆对气膜流场的影响。
1.3 计算方程
1.3.1 N-S方程
在黏性气流中取出一微元体,分别对6个面进行受力分析,如图3所示,图中σ为微元体作用面的压应力,τ为微元体作用面的切应力。

图3 黏性气流微元体
规定x方向为运动方向,则黏性气流微元体在x轴方向的受力由牛顿第二定律计算,即
(4)
(5)
(6)
(7)
fxρdxdydz+
(8)
化简得
(9)
切应力由广义牛顿内摩擦定律确定,即
(10)
压应力为
(11)
式中:v为速度;t为时间;ρ为密度;μ为分子动力黏性系数;f为质量力。
div(υ)为速度的散度,令
(12)
(9)式化简为
(13)
同理可得y,z方向的方程式为
(14)
(15)
1.3.2 层流方程
层流控制方程采用可压缩完全气体雷诺方程,在极坐标下为[12]
(16)
式中:n为轴承转速。
1.3.3 其他方程
轴承承载力方程为
(17)
式中:p(r,θ)为气膜压力分布函数。
摩擦阻力方程为
(19)
气膜刚度方程为
(20)
2 计算流程
轴承气膜承载力计算流程如图4所示,选取螺旋槽动压推力气体轴承设计参数见表1。

图4 轴承气膜承载力的计算流程

表1 螺旋槽动压推力气体轴承参数
利用ICEM软件对计算区域模型的1/12划分网格,采用6面体结构网格,利用mesh功能对周期壁面设置为旋转周期性的边界条件(图2),采用extrude face功能划分的网格如图5所示,为验证数值分析的可靠性,需要进行网格无关性检验,不同节点数的承载力见表2,划分方法1与划分方法2误差约为6%,划分方法2与划分方法3所得承载力误差约为1.5%,当不同节点数误差小于2%时即可用,综合考虑计算机配置情况等本文选用最终生成节点数为81 270,坝区、台区网格为5层,槽区网格为15层。

图5 ICEM网格划分

表2 不同节点数的承载力
3 结果与讨论
采用Pressure-Based求解器,时间设置为稳态,出入口压力均为101 325 Pa,周期边界periodic-1,periodic-2设置为旋转边界,转速n=40 000 r/min,基于N-S方程,本文采用应用较广的SIMPLE算法,为提高精度,方程对流项离散采用二阶迎风格式[13]。
3.1 流态分析
雷诺数判定法的计算公式为[14]
(21)
式中:U为流体流速;L为流体黏性系数。
将U等同为平均旋转线速度v,L等同为气膜总间隙h,re=25.0 mm,ri=12.5 mm,空气密度ρ=1.29 kg/m3,黏度μ=1.789×10-5Pa·s,气膜总间隙h=40 μm,转速n=40 000 r/min,由
(22)
解得Re=2.27。
由雷诺数判定准则知,当Re≤2 300时为层流,2 300
3.2 气体压缩密度分析
气体压缩密度及径向密度分布如图6所示,径向线段为从圆心沿直径方向的一条线段,气流状态为层流。轴承高速旋转时,由于泵入效应,气体不断由入口送入螺旋槽内,在螺旋槽根部受到坝台的阻挡,瞬间气体被压缩,密度和压力增大,起到承载作用;在17.7 mm处即槽根部压缩后,密度达到最大(2.847×10-3kg/m3),之后不断下降,出口处最小。

图6 气体压缩密度分布及径向密度分布
3.3 不同结构参数对轴承气膜承载力的影响
3.3.1 槽深
不同槽深的气膜承载力如图7所示:不同转速下气膜承载力变化趋势相同,泵入型螺旋槽动压推力气体轴承气膜承载力由泵气效应和周向阶梯效应决定,槽深可直接影响气膜承载力,随着槽深的不断增大,轴承的泵入效应不断增强,当槽深为40 μm时泵气效应达到最大,此时气膜承载力最大,说明槽深变化对气膜承载力的影响较大,槽深可取30~50 μm。
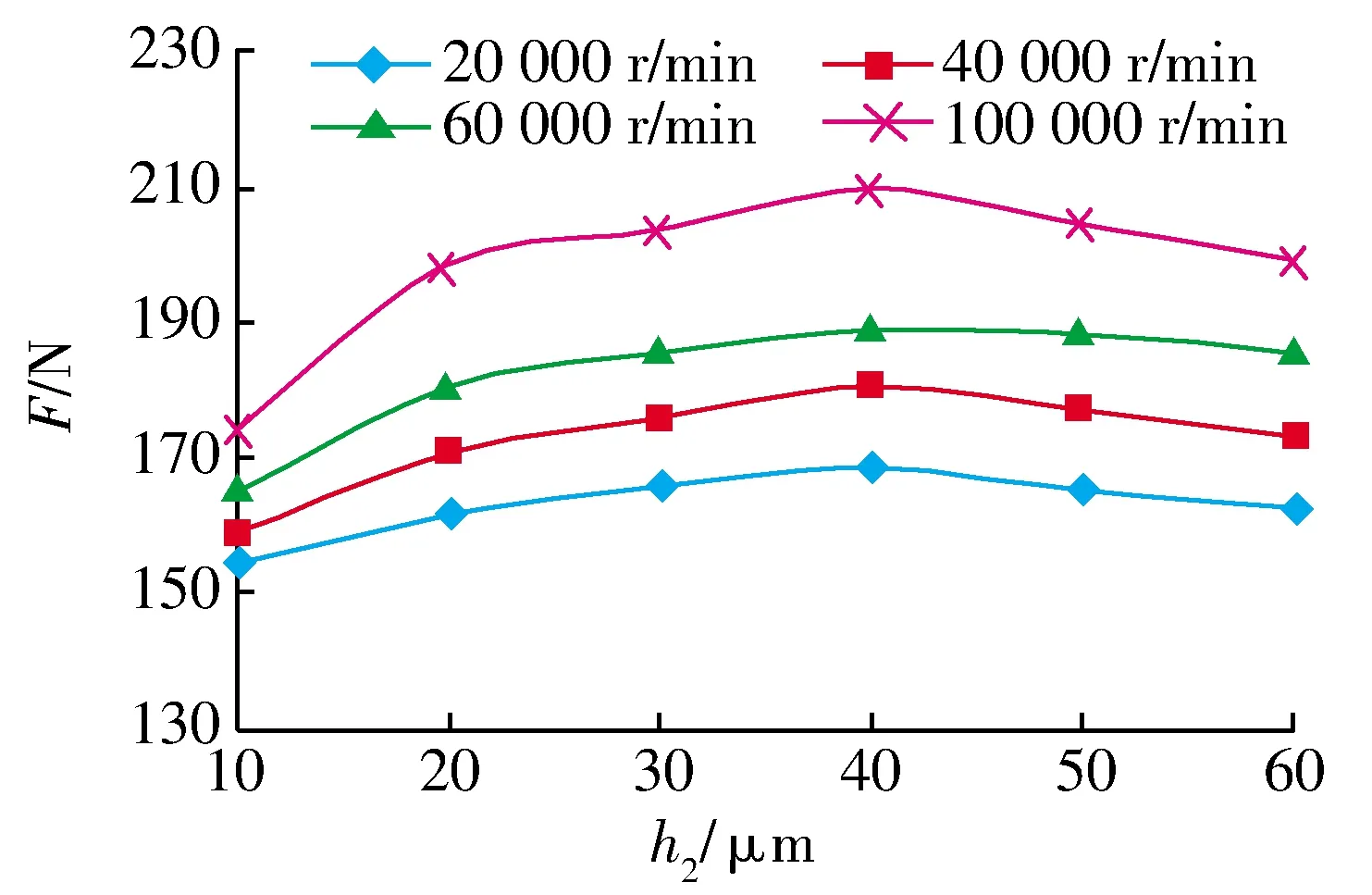
图7 不同槽深的气膜承载力
3.3.2 螺旋角
螺旋角是影响轴承泵气效应的重要参数,不同螺旋角的气膜承载力如图8所示:不同转速下气膜承载力的变化趋势相同,随着螺旋角的增大,轴承的泵气效应增大,气膜承载力增大,螺旋角增大到一定数值后开始下降,在27°时泵气效应达到最大,气膜承载力最大,因此螺旋角可取18°~36°。

图8 不同螺旋角的气膜承载力
3.3.3 台区轴承间隙
不同台区轴承间隙的气膜承载力如图9所示:不同转速下气膜承载力变化趋势相同,随台区轴承间隙增大,气膜承载力不断下降。实际工作中需要较大气膜承载力时可以通过调整台区轴承间隙来实现,不过台区轴承间隙过大时气膜承载力过小,台区轴承间隙过小时轴承与转子之间会有摩擦,因此台区轴承间隙可取4~10 μm。
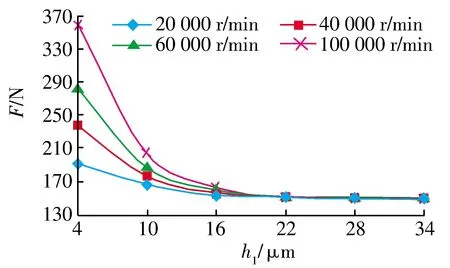
图9 不同台区轴承间隙的气膜承载力
3.3.4 槽内径比
不同槽内径比的气膜承载力如图10所示:不同转速下气膜承载力的变化趋势相同,随着λ的增大,气膜承载力不断增大,当λ为0.6~0.8时,气膜承载力达到最大。结合文献[15]中的λ在0.7附近有一最佳值,可知计算结果的准确性。
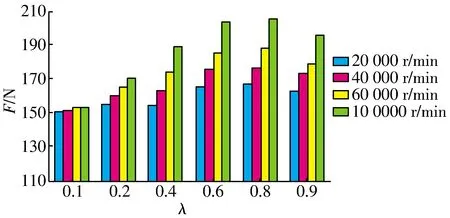
图10 不同槽内径比的气膜承载力
3.3.5 槽宽比
理论上轴承在无槽和全槽时都不会有阶梯效应,因此槽宽比对气膜承载力有一定的影响。不同槽宽比的气膜承载力如图11所示:不同转速下气膜承载力变化的趋势相同,在槽宽比约为0.8时有较大的气膜承载力,槽宽比可取0.7~0.9。

图11 不同槽宽比的气膜承载力
3.3.6 槽数
不同槽数的气膜承载力如图12所示:单从槽数来说,槽数越多,气膜承载力越大;当槽数由5增加到10时,气膜承载力快速增加,之后随着槽数的不断增加,气膜承载力的增加逐渐趋于缓慢,槽数的增加使加工难度增加,所以不能完全只通过增加槽数来提高气膜承载力,槽数可取Ng=12~25。

图12 不同槽数的气膜承载力
3.3.7 槽底结构
平底、凸型、凹型槽的气膜承载力如图13所示,凸、凹型槽是在原有的2 μm的槽深上,在与端面接触的1 μm的槽深中设置为凸面和凹面,凸面和凹面圆周角度为10°。由图13可知,凸型槽的气膜承载力最大,其次为平底槽,最后为凹型槽,并且转速的增大使气膜承载力的差距明显。
3.3.8 螺旋槽结构
部分沟槽可分为泵入型、泵出型,如图14所示。

图13 不同槽底结构的气膜承载力

图14 泵入型、泵出型螺旋槽动压推力气体轴承
不同转速下泵入型、泵出型推力气体轴承的气膜承载力如图15所示:泵入型比泵出型的气膜承载力要高[16],并且随着转速的增大,泵入型气膜承载力增加明显,泵出型气膜承载力增加缓慢,转速从20 000 r/min到120 000 r/min,泵入型气膜承载力从165.72 N增加到212.28 N,泵出型气膜承载力从157.80 N增加到179.16 N,二者最大承载力相差33.12 N,因此在实际运行中可结合工况运行优先选用泵入型轴承。
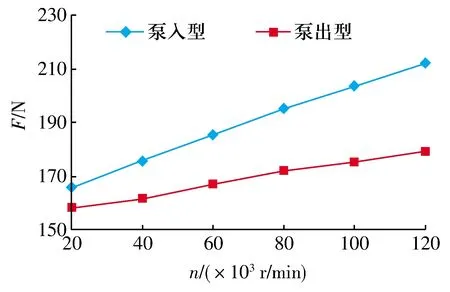
图15 不同工况下泵入型、泵出型推力气体轴承的承载力
4 结论
基于N-S方程,采用有限体积法并结合CFD软件对螺旋槽动压推力气体轴承进行数值模拟,得到以下结论:
1)通过雷诺数判定气膜流动为层流,利用气体的可压缩性,可得到轴承高速旋转中气体的压缩密度分析图,结果显示在槽根处气体密度最大,进而可进行气膜承载力的分析。
2)对比分析不同参数对轴承气膜承载力的影响,根据分析结果给出了槽型几何参数的取值范围:槽深为30~50 μm,螺旋角为18°~36°,台区轴承间隙为4~10 μm,槽内径比为0.6~0.8,槽宽比为0.7~0.9,槽数为12~25,凸型槽>平底槽>凹型槽,泵入型气膜承载力大于泵出型,可优先选用泵入型轴承。
