连续体的有限单元法课程理论与上机课程建设

张一鸣，王雪雅，冯 春，丛俊余

（1.河北工业大学 土木与交通学院，天津 300401；2.中国科学院力学研究所，北京 100190；

3.北京极道成然科技有限公司，北京 100085）

有限单元方法自上世纪50 年代诞生后，伴随计算数学与计算机科学的蓬勃发展，已成为工业界的首选数值分析理论与方法。同时其数学完备，相对直观易理解，计算框架扩展性与可靠性强，是工科本科生与研究生入门数值计算的最佳选择。

另一方面，针对土木工程学生，传统的有限单元法往往更强调结构单元的掌握与教学。例如梁、板、壳类型单元的构造、特性与使用。然而，与建筑工程及桥梁工程不同，在岩土与水利工程中，计算分析中时常会采用连续体单元，即实体单元来模拟岩土体介质，并结合精细化建模来研究工程问题。同时伴随计算机算力的提升，应用连续体单元、考虑非线性过程同时结合多尺度方法，来解决大规模复杂工程问题这一路径也得到了越来越多科研人员的青睐。可以想象在接下来很长一段时期内，连续体单元在工程与科研中会得到更为广泛的应用。

本文即针对如何开展、教授连续体的有限单元方法展开具体的规划与讨论。关于课程的结构设计，我们参考了面向对象的编程过程，从多个“关键知识点”出发，注重“关键点”之间的链接与逻辑关系，尤其是可能存在的继承关系。同时与其他课程例如数值计算与有限元加以区别和类比。在理论授课时深入浅出，以线弹性问题为主，材料非线性问题为辅，几何非线性问题为参考；透彻一维问题，主讲二维问题，选讲三维问题。另一方面，虽然本课程题目是关于“连续体”，但是也会讨论有非连续，即裂缝的情况，也会讨论一些特殊的计算方法与计算策略，如内嵌不连续单元及破裂单元法构造。上机实践是本课程教学的一大重点，本文认为应尽可能采用较为基础高效的编程语言与计算软件，并以开源编译器与开源软件为主，虽然有一定的门槛，但是对于学生后期成长帮助极大，也更适用于团队化协作编程，在当前国际形势下也显得尤为重要。本文后续章节将对课程的具体路径、授课内容与比例、上机操作与考试考察展开讨论。

一、课程路径

本文理论授课包含的关键点如图1 所示，图中实线部分表明关键点间存在较强的逻辑关系，授课过程中不宜忽略，而虚线指向的内容应了解概念，不作为主要授课内容。部分授课关键点与其他课程可能有重叠，授课老师应在第一节课时关注多课程的排课次序，避免授课内容重复，而应基于递进关系更新授课计划，从而加深学生理解与认识。

图1 本文理论授课涉及的关键点

图1 中部分较为基础的内容应重点阐述，例如“实体单元”与“拉格朗日插值方法”以及“高斯积分方法”的内在关联。作者经过多年教学认为，有限单元法方法的基石可高度浓缩于两大方法：弱形式条件∂F=0→∫|∂F-∂G|dx=0 与形函数的引入F（x）=∑N（x）F。前者理论性较强，应注重推导与表达，此处不再赘述。而后者实践性较强，应结合案例教学。在一维情况下的案例包括计算一个沿厚度方向的热传导问题，二维情况则应分析平面弹性力学问题，侧重于分析采用不同单元条件下计算结果的差异。实体单元虽然计算流程较复杂，但其整个计算流程又极为重要，通过纸面计算几个案例可大幅度强化学生对于方法的理解。作者此处建议可采用较少的单元来计算较为基本的案例，例如年代较早的教科书提供了不少经典案例与习题，作者将文献[4]中的一道习题进行扩展，作为案例示于图2 中。图2 所示为一个一端固定，另一端受集中荷载或已知位移的深梁结构，对于这个案例采用有限单元法进行计算时，考虑3 种情况：（1）剖分为2 个三角形常应变单元；（2）剖分为1 个四边形双线性单元；（3）剖分为一个四边形二次单元。通过计算情况（1）让学生初步了解连续体有限单元法计算流程，并且考虑集中荷载或已知位移来研究边界条件的施加；通过计算情况（2）来引入高斯积分，分析高斯点的数量与对应位置、权重，以及其对结果的影响；通过计算情况（3）来介绍高阶单元，与程序计算结果进行对比，阐明高阶单元的适用性。另一方面，也可考虑采用具有对称性的计算算例来进一步简化计算过程。

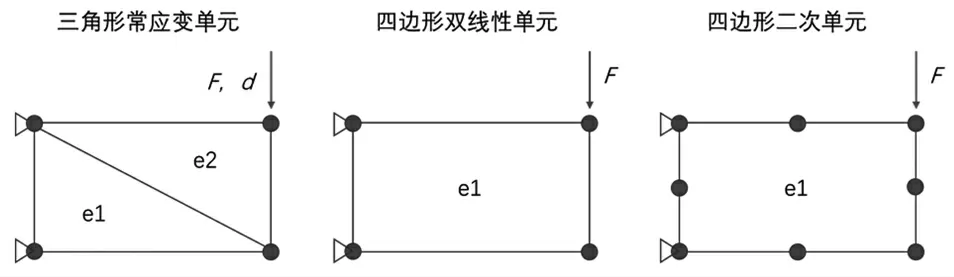
图2 本文推荐的一个二维例题

该案例还可以进一步扩展到三维情况，采用单个三维六面体单元，考虑不同阶次，如图3 的单元示例。通过计算三维情况来分析平面应变问题与平面应力问题分别对应的是哪种厚度方向的约束条件，加深理解。

图3 算例中推荐采用的三维单元

当涉及材料非线性问题时，可退回至一维算例或二维常应变单元的算例。考虑一个给定的应力-应变（σ-ε）关系如理想弹塑性，结合加载时间步，通过隐式（时间）积分，引入牛顿迭代方法，迭代前两步来观察收敛性质。若学生基础较好，也可介绍径向返回算法（return mapping）等高级方法来研究分析材料非线性问题（建议一维）。通过显式（时间）积分，进一步介绍稳定性条件以及动态松弛技术（由于动态松弛技术的适用性与特殊性，本文未将动态松弛方法归类于数值计算工具包）。

最后，当涉及非连续即裂缝的计算时，可阐述基于结点富集的扩展有限元方法（XFEM）的处理方法或者基于单元富集的破裂单元法。其中扩展有限元方法相对较为复杂，可能需要耗费较多学时，以应用及上机操作为主，破裂单元法则相对较为简单，由于有之前有限单元类型的铺垫，授课时可将破裂单元法认为是一种构造类似9结点平面单元的特殊单元来展开，相关内容可参考文献[5]。

二、具体内容比例

建议总课时数约为32 学时，其中理论课课时16 学时，上机课课时16 学时。若将课程作为本科生课程，建议作为三年级（下）课程，作为研究生课程时，建议作为硕士研究生课程。

理论课时分配：数值计算方法1 课时；有限单元方法理论1 课时；实体单元理论与算例计算4 课时；材料非线性理论与算例6 课时，其中隐式（时间）积分计算3课时，显式（时间）积分计算3 课时；扩展有限元2 课时；破裂单元法2 课时。

本文重点阐述上机课程分配：（1）数值计算工具箱4 学时，包括插值函数（一维与二维）2 学时，高斯积分计算（一维与二维）1 学时，牛顿迭代1 学时；（2）二维实体有限单元法（建议采用8 结点二维等参单元）上机指导编程4 学时，其中建模1 学时，单元设计1 学时，组装与边界条件设置1 学时，求解器调用与计算获得结果1 学时；（3）非线性分析4 学时，包括隐式时间积分2 学时，显式时间积分2 学时；（4）破裂单元法1 学时；（5）其他软件如Abaqus，LS-Dyna，Ansys 等演示操作2 学时；（6）上机考试1 学时。

上机课程的具体内容流程：插值函数仅教授拉格朗日插值，完成一维插值算例后，进阶二维三角形单元的面积坐标插值，再完成四边形双线性插值函数构造，同时引入等参单元，获得N、∇N 以及雅可比矩阵的表达。然后可以较为自然地进入高斯积分环节，再转而二维实体有限单元法，完成线弹性问题分析后进入非线性分析，顺序教授牛顿迭代与隐式积分，然后与显式积分作对比，最后过渡到非连续问题与破裂单元法，上机部分的授课流程如图4 所示。

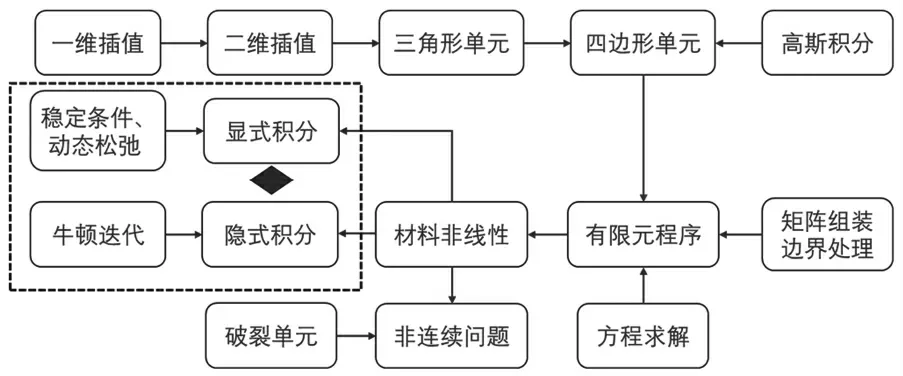
图4 上机操作内容授课流程

三、上机编程要点

上一章节对于课程的上机操作考虑了学习的循序渐进，数值计算工具箱部分可以让学生了解各类子函数、全局变量、结构体的书写格式与调用方法。同时掌握“算法”的程序实现方法，而具体的有限元程序书写则能够锻炼学生对于“工程”的设计与规划能力，即如何将具体功能的子函数组装到模块，实现特定功能，然后将模块再拼装，实现一个任务。

另一方面，如前所述，本文建议应尽可能采用高效基本的编程工具，而非Matlab 一类的商业数值计算软件。而事实上，一旦掌握了较为基础的编程工具后，也可以大幅度降低学习Matlab 的难度。我们建议可选择面向对象的C++或者Python，面向过程的C 或者Fortran。事实上，随着编程软件的发展，现在两种分类有一定模糊性，两类编程语言也在互相借鉴。目前实体有限元程序有大量开源代码供学习，如Calculix，Opensees，但是大部分起点较高，直接对源代码进行理解存在一定难度。无论采用面向对象还是面向过程编程语言，作者认为实体有限元程序中存在诸多“要素”，我们将主要“要素”列于图5 中。

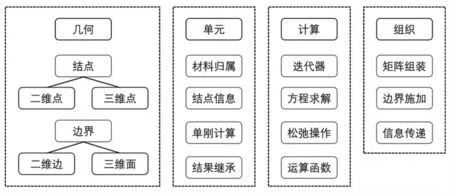
图5 实体有限元程序设计中的一些要点与功能

其中的几何部分，与建模程序的几何部分有一定相似性，但又有所不同。我们进行了简单的展开，每个要素可以根据不同情况进行进一步扩展，其所包含的信息、函数、数据方法在不同条件下也存在差异，其他部分也可作类似展开。对于学生的考查可侧重于对相关功能的要素归类，或者子功能的具体实现。对于一些较为复杂的“黑箱式”功能，例如大规模线性方程组求解，可通过熟悉开源代码的输入和输出格式，直接书写API 接口取用，这样可以锻炼学生对于既有代码的调用能力。

本课程的考试建议以上机操作为主，可设置多类必须通过编程来求解的选择题与计算题，要求学生必须通过现场书写代码，调试，运行后获得结果答题。例如提供结点位移求解某个单元某个高斯点的应变值，提供材料信息计算某个单元的刚度矩阵，提供裂缝法方向求解破裂单元的整体刚度矩阵等。

四、结论与展望

CAE 即计算机辅助工程分析、设计、优化，是一种新时代下的国之重器，各国对于CAE 核心技术都极为重视。而CAE 技术的自主研发离不开优秀CAE 开发人员的发掘与培养，这是典型的工程-软件设计交叉学科。本文对于连续体的有限单元法课程理论与上机课程进行了设计与探讨，对于授课内容、逻辑结构、课时分配、上机编程进行了规划。相信本课程的顺利建设对于培养中国制造2025 背景下的优秀工程人才有一定的推动作用。