一个基本模型的运用

牟方田

首先，给出一个关于等腰三角形的基本模型.

如图1，OC平分∠AOB，CD∥OB，CD交OA于D点，则△OCD是等腰三角形．

证明：∵OC平分∠AOB，

∴∠1=∠2．

∵CD∥OB，∴∠2=∠3．

∴∠1=∠3，DO=DC，即△OCD是等腰三角形．

由图1知，“角平分线＋平行线”就能构造出等腰三角形．这个关于等腰三角形的基本模型随处可见，应用广泛，要加以重视．

一、判断等腰三角形的个数

例1如图2，在△ABC中，AB=AC，BD是∠ABC的平分线，DE∥BC，DF∥AB．请问：图中除了△ABC外，还有多少个等腰三角形？

解析：由“DE∥BC”可推知△ADE是等腰三角形，同理△CDF也是等腰三角形.由于BD是∠ABC的平分线，由等腰三角形的基本模型可知△BDE、△BDF都是等腰三角形．

故图中还有4个等腰三角形：△ADE、△BDE、△BDF、△CDF．

二、求线段的长

例2如图3，四边形ABCD是平行四边形（对边平行的四边形），AB=3 cm，AD=5 cm.∠B的平分线与CD的延长线交于E点，BE与 AD交于点F.试计算AF、DE的长．

解析：由于BE平分∠ABC，AF∥BC，由等腰三角形的基本模型知△ABF是等腰三角形，从而可知△DEF也是等腰三角形，所以AF=AB=3 cm．而DF=AD-AF=2（cm），故DE=DF=2 cm．

三、求三角形的周长

例3如图4，在△ABC中，BC=5 cm，BP、CP分别是∠ABC和∠ACB的平分线.PD∥AB，PE∥AC，求△PDE的周长．

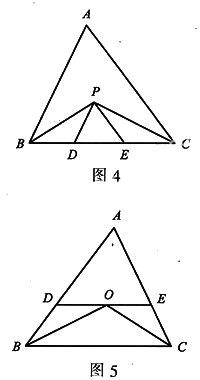
解析：由等腰三角形的基本模型知△BDP、△CEP都是等腰三角形，则PD=BD，PE=CE，于是△PDE的周长转化为BC边的长．

∴△PDE的周长=BC=5 cm．

四、探究线段之间的关系

例4如图5，在△ABC中，∠ABC、∠ACB的平分线相交于点O.过点O作BC的平行线，分别交AB、AC于点D、E．先猜想线段BD、CE、DE之间的关系，再说明理由．

解析：由等腰三角形的基本模型，知△BDO、△CEO都是等腰三角形，则DO=DB，EO=EC，于是有DE=BD+CE．