数形结合思想在初中数学解题中的应用
2022-06-01韩军

摘要:初中数学的教学中运用数形结合,通常能够使学生学习数学知识的能力得到切实提高.鉴于此,本文主要对数形结合及其在初中数学解题中的运用重要性与问题进行分析,并提出数形结合在初中数学具体解题中的应用策略,从而使学生的思考与探究能力得以提高的同时,实现初中數学的教学质量与效率提升.
关键词:初中数学;数形结合思想;解题;应用
中图分类号:G632文献标识码:A文章编号:1008-0333(2022)14-0035-03
收稿日期:2022-02-15
作者简介:韩军(1975.10-),男,甘肃省靖远人,本科,中学高级教师,从事初中数学教学研究.
数形结合通常指在数学信息不发生改变的情况下,数据与图形的有效转换,将相关数据精密的呈现在图形上,以图形上出现的变化,对数据变化进行理解,并经过数据了解到图形的状态.因此,在对数学问题进行解决时,需注重图形与数值的有效结合,以促使学生通过眼睛观看到数据的变化,这不仅能够使学生对于数学知识的学习兴趣得以提高,而且还能使数学问题更为简单,促进学生有效解决相关数学问题,从而使学生形成良好的学习与思考习惯.初中阶段的数学解题中,教师可通过相应的教学方法对学生的学习习惯进行培养,以促使学生形成相应的自学能力.基于此,数学教师在解题教学中,需注重数形结合的思想融入,促进学生对于数学知识的理解,以数形结合的思想解决相关应用题,以此为数学学科的实践问题解决奠定夯实的基础,并促进学生自身的水平提高.同时,数形结合还有助于学生的理解力以及逻辑能力的提高,引导学生由数学题目中找到可应用的内容,以画图表达出内容,以实现数学题的简单化、明了化,以实现数学题的有效解决.
1 数形结合思想及其思维培养的意义
1.1 数形结合思想概述
数形结合运用到的是数和形的对应关系,其能够使数与形之间实现有效转换,以便于数学难题的有效解决,许多问题都能通过该原理,获得更为便捷的解题方式,许多的数学知识都抽象无法有效理解,如能通过数形的有效转化,就更便于理解,属于初中数学实际解题中的重要思想.通过数形结合思想的运用,主要是对条件与结论之间的联系进行考察,将其联系通过图形或数轴实施表达,不仅能通过几何与代数实现数学问题的解决,而且还能使解题的效率与准确率得到有效提高.
1.2 数形结合思维培养的意义
首先,有助于学生直觉思维的发展.对于直觉思维而言,其主要指不通过严格逻辑推理的过程,在第一时间对数学问题做出合理猜测与设想,直到数学问题的解决,其并非是毫无根据的,而是来源于新旧知识的联系、衔接与积累.通过直觉思维实现问题解决,就需做到认真观察、猜测、联想与归纳.而数形结合的思维培养,则需学生形成相应的自觉思维,需学生在较短的时间实现几何模型的构建,依据给出的已知条件,实现函数或者几何图形的构造,以实现数学问题的直观形象的解决.
其次,有助于学生学习数学知识的兴趣提高.初中数学的解题过程中,对学生而言是极为枯燥的,且涉及到一定的思维与逻辑,具有较大的难度,这就会影响到学生对于数学知识的学习兴趣.想要避免该现象出现,数学教师在解题教学中,就需通过数形结合的思想,将数学题和图形有效结合,以促进学生学习兴趣提高的同时,吸引学生的学习注意力,促进学生对于数学知识的学习难度降低,以促使学生积极主动接受数学知识的同时,促进学生自身的学习能力提高.
2 数形结合在初中数学解题教学中的问题
2.1 对数形结合的方法缺乏重视
经过调查显示,数形结合在初中数学的解题中没有得到充足的重视.由此可知,数形结合普及,不仅需教师自身具备相应的数形结合意识,而且还需创设出通过数形结合的方法进行问题解决的环境,且学生也需充分的认识与了解到数形结合在解题中的重要性.
2.2 对数形结合的价值缺乏认识
初中数学的传统化学习中,学生对于数学知识的学习较为吃力,这就使学生无法充分了解到何为数形结合,无法通过数形结合的灵活运用,促进数学问题的解决,也无法了解到数形结合的简便性.许多原因致使学生无法充分认识到数形结合的重要性.
2.3 对数形结合的方法缺乏应用
虽然教师们都知道数形结合运用的重要性,但在具体教学中,却缺乏灵活的应用.同时,部分数学教师对于数形结合的实际应用不够了解,在具体教学中也不会用到该方法,且学生具备向师性,这就使教师的不了解成为学生的不了解,也无法了解到数形结合的重要性,这就使学生在解决数学问题的时候,不会应用数形结合,也不会通过数形结合促进学习效率的提高.
3 数形结合思想在初中数学解题中的应用策略
3.1 利用数轴促进绝对值问题解决
初中阶段的数学教学中,教师在教学初始已引入了数轴,由于数轴和实数构建了一一对应关系,并为相反数、绝对值等全新概念等赋予了几何意义.在对绝对值定义开展讲解时,需对数轴知识进行学习,并引入实际问题.
例如,数轴上点A至原点之间的距离是3,点B至原点之间的距离是2,求A、B两点之间的距离.
由数轴上来看,至原点的距离是3的点需分别置于原点的两侧且和原点之间的距离都是3个单位长度,因此,两个点表示的数分别是+3与-3,也就是点A表示+3与-3,点B表示+2与-2,详见图1.此时,AB两点之间的距离是1个单位长度或者是5个单位长度.
评析在本题中,绝对值的概念是能够直接应用的,若不做图,就会认为题目抽象,且容易丢一种情况,但将数值呈现于数轴上,不仅形象且直观,而且还能促进数和形的有效融合,以深化学生对于知识的印象.
3.2 利用函数图像促进方程、不等式问题解决
平面直角坐标系通常是在数轴后,又一个将代数和几何有效衔接的工具,其扩大为有序实数对与平面中所有点都是一一对应的关系,将点转变为线与面,更为初中时期重要的知识,即函数,提供了有效的生长土壤.而函数能够与许多的知识有效结合,构成具有较强综合性的数学题,如其能与不等式、方程等相联系,通过函数图像对不等式解的取值范围、方程的根等进行解决.此时,教师可引导学生通过函数图像对相关数学问题进行明了、直观的解决,主要有以下形式.
3.2.1 函数与方程、方程组
一次函数y=kx+b(k≠0,k,b是常数)
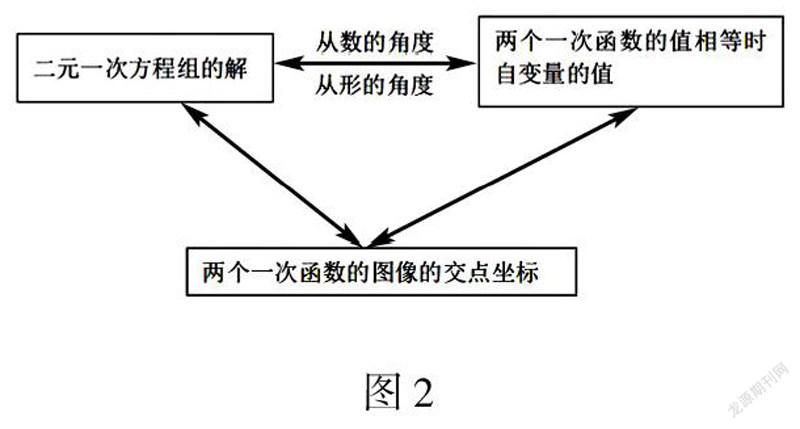
①如果函数y=0的时候,会得出一元一次方程kx+b=0,这个时候,自变量x的值就是方程kx+b=0的解,其表示为图像上则是一次函数图像和x轴交点的横坐标.
②如果x、y是两个变量,因此,一次函数可看作为二元一次的方程kx-y+b=0.
③求取方程组的解通常就是求取两个函数值相等的时候自变量的数值.二元一次方程组和一次函数的关系详见图2.
④二次函数y=ax+bx+c(a、b、c为常数,a≠0)图像和x轴的交点坐标是(x,0)、(x,0),即x、x为方程ax+bx+c=0的实数根,若y=ax+bx+c的图像和x轴无交点,那么,方程ax+bx+c=0没有实数根.二次函数y=ax+bx+c(a、b、c为常数,a≠0)的具体图像位于x轴上方的全部点的横坐标的集合是一元二次不等式ax+bx+c>0的全部解集,而图像位于x轴下方全部点的横坐标集合是一元二次不等式ax+bx+c<0的全部解集.通过图像进行方程解答,可通过二次函数y=ax+bx+c(a、b、c为常数,a≠0)和一元二次方程ax+bx+c=0之间的关系,进行图形绘制,以做出解答.在对ax=bx+c(a≠0)进行求解时,可将y=ax和y=bx+c两个图像分别画出,并找出两个函数图像的交点坐标.
3.2.2 函数和具体应用
具体的应用题一直属于教师头疼、学生害怕的题,但是,学习数学知识的主要目的就是进行实际问题的解决,也就是具体应用.因此,找出准确的方法,多加练习与总结极为重要.最为典型的就是通过平面几何图形,将问题图形化,通过图形进行问题的直观解决,以促使问题的解答更加简单、明了.
例如,某厂销售一种面包,未销售出去的可退回厂家,依据统计表明,单价为7角的时候,每天可售160个,售价每增加1角,每天少售20个,每个面包成本是5角,设面包单价是x角,每天销售利润是y角.
(1)通过x代数表示利润与售卖个数的关系;
(2)求取y与x的函数关系式;
(3)面包单价为多少的时候,利润最大?最大是多少?
分析二次函数主要反映了变量的数量关系与其变化规律的函数形式,基于此,在对具体问题和二次函数的问题进行研究时,可构建数学模型,通过二次函数具备的性质进行问题解决,通过数形结合,则能有效呈现该思想.
综上所述,数形结合属于极其重要的一种数学思想,在数学试题的解决中通常具有无法替代的作用,能够将许多抽象化数学问题通过直观形象的方式展现.因此,初中数学的解题教学中,需注重数形結合思想的运用,将复杂的数学问题简易化,从而使学生的解题效率与准确率得以提高的同时,实现数学教学的整体质量提升.
参考文献:
[1] 李成绪.数形结合思想在初中数学解题教学中的应用分析[J].试题与研究:教学论坛,2020(36):1.
[2] 周宇.浅谈数形结合思想在初中数学解题教学中的应用[J].山海经:教育前沿,2020(7):1.
[3] 罗惠庭.数形结合思想在初中数学解题教学中的渗透策略[J].中学数学研究(下半月),2018(10):17-19.
[4] 赵以顶.数形结合思想在初中数学教学中应用研究[J].数学学习与研究,2018(04):43.
[责任编辑:李璟]
