儿童早期数学能力与学习品质的发展趋势及其关系变化

杨琼 蔡军

［摘 要］ 儿童在学前阶段形成的数学能力与学习品质如果能够在进入小学后继续发展，将不仅有助于巩固学前教育的成果，而且能更有效地预测儿童将来的学业成就。本研究以172名幼儿园大班和小学一年级儿童为研究对象，运用经Rasch模型修订的早期数学能力评估工具和自编的学习品质量表，考察儿童从幼儿园大班到小学一年级的数学能力与学习品质的发展情况及其关系，以验证儿童的早期数学能力与学习品质是否在小学获得了持续发展及其关系是否发生了变化。结果发现，儿童的数学能力表现出显著的年级差异，一年级得分显著高于大班；儿童的学习品质没有随其进入小学而增长，相反呈现出下降趋势；学习品质对大班儿童数学能力的预测作用更强，解释率达71%，对一年级儿童数学能力的预测作用有所减弱，解释率仅为45%；学习品质中的自我调控与解释性维度对大班与一年级儿童的数学能力均有预测作用；對于大班儿童来说，学习品质中的独立性与探究性维度是其数学能力的另一重要预测变量；对于一年级儿童而言，其数学能力的另一重要预测变量是学习品质中的积极性与主动性维度。可见，我们非常有必要关注儿童早期数学能力与学习品质在幼小衔接阶段的持续发展，依循儿童数学学习发展轨迹，建构一条清晰的从幼儿园到小学的数学学习与发展之路，同时通过多方协同促进儿童学习品质的养成与发展，坚持小学阶段也要注重儿童学习品质的培养，以积极发挥学习品质对儿童数学学习的支持作用。

［关键词］ 数学能力；学习品质；幼小衔接；Rasch模型

一、问题提出

儿童早期数学能力为儿童顺利有效完成数学活动所具备的个性心理特征，[1]具体表现为儿童对数、形状/空间、测量、模式知识和技能的理解与运用的能力。[2]早期数学能力不仅能预测其之后的数学学业成就，[3]而且相比早期读写能力和社会情感能力更能预测其未来的阅读成就。[4][5][6]早期数学能力较好的儿童将来也能获得较高的社会经济地位。[7]由此可见，数学思维是一种基础性的认知能力。早期数学能力的重要性引起越来越多研究者和政策制定者对儿童早期数学能力发展过程和轨迹的关注，大量的研究描述了学前儿童在数感、模式等方面的发展特征，[8][9]一些纵向研究也表明，学前儿童数学能力能显著预测小学三年级、五年级和初中的数学成绩。[10][11]有研究进一步指出，儿童在大班到一年级期间增长的数学能力相比其在学前期间的数学能力更能预测儿童小学和高中的数学成就。[12][13]幼儿园大班到小学一年级是儿童发展道路上重要的教育转折期，儿童在这一阶段经历诸多转变：一是从生活化探究性学习到结构化课程学习；二是从关注个体兴趣到注重集体发展；三是从注重儿童过程性评价到以成绩评估儿童能力。两个阶段在教育观念、课程设置和教学方式上存在着诸多不同，这种不同使儿童面临着身体、心理、学习习惯和能力等多方面的挑战。因此，对于儿童来说，从幼儿园到小学的过渡是他们成长过程中的关键一大步（a big step）。研究发现，若儿童能在这个关键阶段获得积极体验，对其未来社会性、情绪情感和学业成就发展都有良好的促进作用。[14][15]为帮助儿童顺利实现从幼儿园到小学的过渡，学前研究者和实践者做了大量的工作，包括重视儿童早期数学能力的发展。[16]然而，若只重视学前期儿童数学能力培养，忽视小学低年级数学教育，那么学前阶段对儿童产生的积极影响也会随着儿童进入小学阶段而逐渐减弱（fade out）。[17]这反映了学前阶段的投入固然重要，但不足以确保儿童能够持续发展。相反，有研究指出，若为幼儿园大班和小学一年级儿童均提供高质量的数学教育，那么儿童的数学能力将会得到持续发展。[18]因此，研究者要尤其关注幼儿园大班和小学一年级儿童早期数学能力的发展，为将来的数学学习打下重要的基础。

要想了解幼儿园大班和小学一年级儿童数学能力的发展规律和差异，就需要一个能够同时适用于大班和小学一年级儿童的数学能力评估工具。目前，国内被广泛使用的工具是由金斯伯格（Ginsburg）等人开发的《早期数学能力测验第三版》（Test of Early Mathematics Ability 3，TEMA 3），主要用于测试3至8岁11个月儿童非正式数学能力和正式数学能力。[19]康丹将其引入国内，但仅考察其在学前儿童中的适用性，[20]且该量表存在的最大弊端是仅侧重对儿童计数与运算能力的考察，忽视对空间、几何、模式等其他方面能力的测评。因此，本研究拟引进由克莱门茨（Clements）等人开发的《基于研究的早期数学能力评估工具》（Research based Early Mathematics Assessment， REMA），该量表具有以下特点：[21]第一，测试对象涵盖学前和小学低年级儿童，能评估3～8岁儿童的数学能力；第二，评估内容不仅包含已被实证证明的早期数学核心内容（数与运算、空间—几何、测量和模式），还关注幼儿解决问题的思考过程，记录解决问题的策略；第三，每个项目是基于儿童学习发展轨迹（learning trajectories）编制的，研究者都是先回顾大量文献，描述儿童在这个项目中的发展轨迹，了解了儿童的思维和概念发展变化后而设计的；第四，项目是通过儿童操作材料来评估其数学表现；第五，已有研究证明REMA评估工具具有良好的内容效度（content validity）、表面效度（face validity）①和同时效度（concurrent validity）②。[22][23]但考虑到中西文化和社会背景的差异，有必要采用科学有效的方法评估REMA量表在我国大班和一年级儿童中的适用性。基于经典测量理论（Classical Test Theory， CTT）检测量表质量的传统方法，无法避免题目难度估计和儿童能力估计的相互干扰，不能实现测量的客观等距目标，[24]而以项目反应理论为基础的Rasch模型，能够同时将项目难度和被试难度放在同一标尺上。因此，本研究试图运用Rasch模型对REMA量表进行修订，以期形成一套适用于评估幼儿园大班和小学一年级儿童早期数学能力的高质量评估工具。

某些认知能力被认为是影响儿童早期数学能力发展的因素，有研究发现执行功能与早期数学能力有着直接或间接的联系，[25]也有研究发现工作记忆对大班和一年级儿童数学发展有直接作用等。[26]梳理已有研究发现研究者更多是关注儿童自身抽象思维能力发展的积极影响，早期数学能力的发展不仅受自身认知能力的影响，还受学习品质的影响。学习品质（Approaches to Learning）即儿童参与学习活动或达成学习目标所表现的一系列行为、认知与态度倾向。[27]尽管不同的研究可能涵盖不同的成分，但一般来说，学习品质包括积极性、主动性、自我调控、独立性、探究性、专注性、坚持性、反思与解释性、问题解决性等方面。[28][29][30]学习品质在儿童早期学习与毕生发展中具有重要的奠基性作用。[31]若儿童对数学活动感兴趣，就会更积极探索具体操作材料，且能长时间地坚持探究，数学能力就会获得持续的发展。越来越多的研究表明，儿童早期学习品质不仅能预测早期数学能力，[32][33][34]而且也能预测三年级、五年级的数学学业成就。[35][36]研究者不仅将学习品质作为一个整体来考察其与儿童早期数学发展的关系，还探讨了各分维度对早期数学能力的影响，如有研究发现学习品质各分维度与数学能力呈现显著正相关，[37][38]其中坚持性最能预测儿童的正式数学能力。[39][40][41]而张莉等人的研究却发现自我控制力才是早期数学能力最有效的预测变量。[42]但是，这些研究关注的是学前阶段或小学一年级，并未对两者进行比较。国外有少量研究分析了儿童从学前到一年级期间学习品质的发展轨迹，其中有研究发现这个阶段的学习品质呈高水平发展且呈略有增长，值得注意的是从大班到一年级这个阶段，学习品质的发展是相对稳定的。且儿童的学习品质表现出显著的个体差异，一些孩子随着年龄的增长，学习品质也在快速增长，相反，一些孩子的学习品质在下降。[43]而吴（Wu）的研究结果却表明从幼儿园到三年级，儿童的学习热情、坚持力、注意力等学习品质均呈下降趋势。[44]鉴于研究结果的不一致，有必要深入探究儿童早期学习品质从幼儿园大班到小学一年级的发展趋势。研究者还进一步发现学习品质对儿童从幼儿园大班过渡到小学一年级期间的数学能力起着积极作用，[45]但是这一研究并未解析学习品质具体维度对大班和一年级儿童的作用。

鉴于此，探析幼儿园大班和小学一年级儿童早期数学能力和学习品质发展趋势，厘清学习品质的具体维度与早期数学能力的关系显得尤为重要。一方面能够对当下学前和小学低年级数学课程设置和学习方式提供可参考意见，建构出一条更为清晰的从幼儿园到小学的儿童数学学习与发展之路。另一方面能帮助广大家长和教师深度理解学习品质对儿童早期数学能力产生影响的机制，从而做好科学的入学准备和入学适应。

二、研究方法

（一）研究对象

本研究选取陕西省西安市两所幼儿园和两所小学作为样本来源学校，分别在幼儿园大班、小学一年级随机抽取被试，共179人，剔除因请假而未完成测验任务的7人，有效被试为172人。其中大班82人（男生42人，女生40人），平均年龄为6.15岁，一年级90人（男生42人，女生48人），平均年龄为7.22岁。实验前研究者与班级教师和家长取得联系，告知研究目的和内容，获得儿童参与研究的许可。本研究采用的是同一批被试分别完成早期数学能力评估工具和学习品质问卷的修订和测评的方式。

（二）研究工具

《基于研究的早期数学能力评估工具》包括两部分：A部分测试儿童数数、认数和加减能力；B部分测试空间—几何、测量和模式能力。[46]所有项目经由2名学前教育专业博士生和4名硕士生共同翻译完成。REMA共有158个项目，其中有142个项目为两点计分，正确计为1分，错误计为0分；有12个项目为三点计分，即正确计1分，部分正确计0.5分，错误计为0分；有4个项目是根据权重计分。评估的实施有与特定年龄相对应的起始点，大班儿童从项目13开始，一年级儿童从项目33开始，儿童连续答错5个项目，则停止评估。合计A部分和B部分分数即为儿童最后数学能力得分，得分越高，表明被试数学能力越强。在不改变原评估工具具体内容基础上，研究者首先根据文化适应性对个别项目的语言进行修正，确保通俗易懂，再使用Rasch模型测量理论中的部分给分模型（Partial Crefit Model）对项目进行初次修订，[47]改进不合理评分标准，删除不符合拟合指标项目，最终形成正式评估工具。

《儿童学习品质评价量表》是在参考徐晶晶的《学前儿童学习品质观察评定表》、王宝华等人的《儿童学习品质观察评定量表》的基础上编制而成的。[48][49]采用Likert 3點计分（0代表“几乎不”，1代表“有时”，2代表“总是”），每个维度相加的得分即总维度得分，得分越高表明学习品质越好。对该量表进行项目分析和因子分析后，构成积极性与主动性、自我调控与解释性、独立性与探究性、专注性与坚持性等4个维度，共计18个项目。其中积极性与主动性是指儿童愿意参与数学学习活动，肯接受数学任务（共4个项目，题目如能够积极参与数学任务，对数学任务和材料感兴趣）；自我调控与反思解释是指个体对认知和情绪的控制以及儿童能够清楚地解释自己的行为（共4个项目，题目如能够自我平复情绪、能够清楚说出自己解决问题的方法以及采用这种方法的原因）；独立性与探究性指儿童能独立完成任务，对新知识表现出强烈的好奇心和探究愿望（共5个项目，题目如能够理解数学任务，并能独立完成数学任务，对有挑战性的数学任务表现出好奇和想探究的欲望）；专注性与坚持性指对数学任务的坚持性以及注意力的维持水平（共5个项目，题目如在做数学任务中不轻易被打扰）。经检验其KMO系数为0.902，累计解释变异量为66.30%，各项目因子载荷量介于0.49～0.85之间，该量表各因子的α系数在0.931以上，说明该量表具有良好的信效度。

（三）研究过程

早期数学能力评估由经过训练的心理学或者学前教育学的硕士生完成。实验前，先由研究者对主试进行培训，讲解评估内容和操作步骤，再让主试两两结对，按照评估指导手册练习，直到熟悉整个评估内容和操作步骤后开展正式测评。学校和幼儿园为主试提供安静的场所，主试按照指导手册的要求，以游戏的形式展开测评，主试提供积木、圆片、卡片、各种几何图形、七巧板等数学材料，儿童根据主试要求完成相应任务，主试记录儿童的反应。早期数学能力评估工具分为A部分和B部分，每部分测评大约需30分钟完成，若幼儿在中途表现出疲惫，则暂停测试，适当休息后再继续。

《儿童学习品质评价量表》由教师填写，研究者首先向各班级教师阐明具体的行为指标和评分规则，再由教师基于对儿童长期在数学任务中的行为表现来评定。量表在学期中由研究者发放下去，学期末统一回收，量表回收率100%。

（四）数据分析

本研究对早期数学能力评估工具修订采用Winsteps软件完成Rasch模型分析，其中主要包括单维性检验、概率曲线图、怀特图、项目拟合情况；对早期数学能力和学习品质发展特征及其关系研究采用SPSS完成描述性分析、差异性分析、相关分析、回归分析。

三、研究结果与分析

（一）《基于研究的早期数学能力评估工具》的质量分析

首先，本研究根据Linacre提出的第一准则，删除反应低于10的项目，[50]共10项。其次，使用概率曲线图（Probability Curves）考察所有项目评分规则的制定情况，将12项评分标准设计不合理的，均改为“0，1”评分标准，调整后的项目评分规则达到理想状态，每一个选项都有一个明显的波峰，且每条曲线都是平直的。[51]第三，经过6次逐步删除项目的迭代分析，删除不符合拟合指标52项，[52]最终保留了106个项目。其中A部分71个项目，B部分35个项目，再次使用Rasch模型进行信效度分析。

本研究使用Rasch模型的残差主成分（Standardized Residual Contrast Plot）分析来检验数据残差中是否存在另一个维度。结果表明，大多数项目在-0.5至0.5之间，符合单维性。[53]只有A和a超出了许可范围，但是仔细检查了这2个项目，它们并不能形成一个有解释意义的因子维度。因此，修订后评估工具具有单维性，能够共同反映出儿童的早期数学能力。

Rasch模型通过对数转换，将数据转换成等距的logit值，把被试的能力与项目难度置于同一量尺中进行比较，直观地展现项目难度与被试能力、项目之间、被试之间的关系。[54]本研究中多数被试都有与之对应的项目，项目与项目之间的难度分布较均匀，被试能力分布也较为理想，中间多，两边少。整体来说，修订后的早期数学能力评估工具的项目水平与其对应的被试能力水平基本一致。

模型拟合度包括标准误（SE）、内外合适度（Infit /Outfit MNSQ）和相关系数（C0RR.），标准误反映项目的稳定性，内外合适度反映评估数据与Rasch模型的拟合度。分析结果表明，该评估工具能较稳定地评估被试的水平，各个项目的内外合适度指标在0.5～1.5之间，符合Rasch模型，[55]所有项目与总分的点二列相关都是正向的。整体而言，修订后的早期数学能力评估工具各项指标均在接受范围内，与模型拟合较好。

测验信度方面主要采用测验项目及被试的分离系数（Separation）和信度（Reliability），分离系数表明项目之间的区分效果。结果如表1所示，项目分离系数为5.30，约等于标准值6，[56]说明项目之间区分效果较好，被试和项目信度均为0.9以上，符合心理测量学的要求。总体而言，修订后的早期数学能力评估工具具有较好的信效度，能够作为测量大班和一年级儿童数学能力的评估工具。

（二）大班和一年级儿童的数学能力与学习品质

1． 大班和一年级儿童数学能力的差异分析

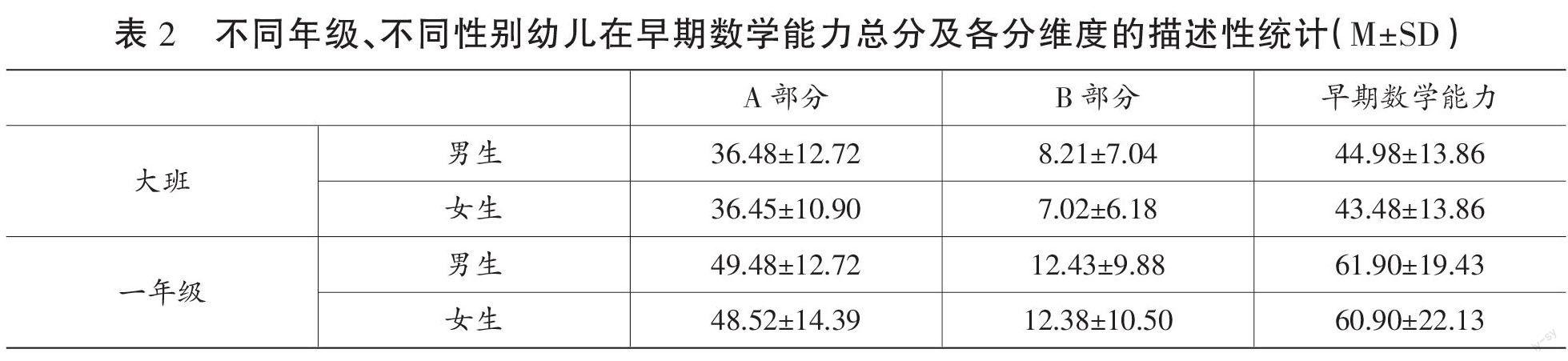
表2呈现了不同年级、不同性别儿童在早期数学能力总分及各分维度上的得分情况，进一步以性别、年级为自变量，早期数学能力总分及各维度得分为因变量进行多因素方差分析。结果表明，性别在A部分（F（1，172）=0.115，p>0.05，ηp2=0.001）、B部分（F（1，172）=0.219，p>0.05，ηp2=0.001）、早期数学能力总分（F（1，172）=0.210，p>0.05，ηp2=0.001）上主效应不显著。年级在A部分（F（1，172）=43.851，p<0.001，ηp2=0.207）、B部分（F（1，172）=12.943，p<0.001，ηp2=0.072）、早期数学能力总分（F（1，172）=39.378，p<0.001，ηp2=0.190）上主效应显著。性别与年级在A部分（F（1，172）=0.030，p>0.05，ηp2=0.000）、B部分（F（1，172）=0.182，p>0.05，ηp2=0.001）、早期数学能力总分（F（1，172）=0.008，p>0.05，ηp2=0.000）上交互作用不显著。事后比较结果显示，一年级得分显著高于大班。

2. 大班和一年级儿童学习品质的差异分析

不同年级、不同性别儿童在学习品质及其四大维度上的得分情况见表3，进一步以性别、年级为自变量，以学习品质及各维度得分为因变量进行多因素方差分析。结果表明，性别在积极性与主动性（F（1，172）=0.953，p>0.05，ηp2=0.006）、自我调控与解释性（F（1，172）=0.019，p>0.05，ηp2=0.000）、独立性与探究性（F（1，172）=0.677，p>0.05，ηp2=0.004）、專注性与坚持性（F（1，172）=0.009，p>0.05，ηp2=0.000）、学习品质（F（1，172）=0.283，p>0.05，ηp2=0.002）上主效应不显著。年级在积极性与主动性（F（1，172）=10.843，p<0.01，ηp2=0.061）、专注性与坚持性（F（1，172）=5.867，p<0.05，ηp2=0.034）、学习品质（F（1，172）=6.327，p<0.05，ηp2=0.036）上主效应显著，在自我调控与解释性（F（1，172）=3.60，p>0.05，ηp2=0.061）、独立性与探究性（F（1，172）=1.133，p>0.05，ηp2=0.007）上主效应不显著。性别与年级在积极性与主动性（F（1，172）=0.026，p>0.05，ηp2=0.002）、自我调控与解释性（F（1，172）=0.122，p>0.05，ηp2=0.001）、独立性与探究性（F（1，172）=0.105，p>0.05，ηp2=0.001）、专注性与坚持性（F（1，172）=0.150，p>0.05，ηp2=0.001）、学习品质（F（1，172）=0.056，p>0.05，ηp2=0.000）上交互作用不显著。事后比较结果显示，在积极性与主动性、专注性与坚持性、学习品质总维度上，大班得分显著高于一年级，在自我调控与解释性、独立性与探究性上，两个年级差异不显著。

3. 大班和一年级儿童的数学能力与学习品质的关系分析

对大班和一年级儿童学习品质的总维度及四个子维度与早期数学能力的总维度及两个子维度进行相关分析，结果如表4。研究发现这两个年龄段早期数学能力总分及子维度与学习品质总分及子维度之间呈显著正相关，相关系数在0.25～0.80之间，表明不论是幼儿园大班还是小学一年级，早期数学能力与学习品质之间都有密切关联。

进一步考察不同阶段儿童学习品质对早期数学能力的预测作用，以学习品质四个维度为自变量，以早期数学能力为因变量进行回归分析，结果见表5。研究发现无论是大班还是一年级，学习品质中自我调控与解释性对早期数学能力均有预测作用。不同的是，对于大班儿童早期数学能力而言，独立性与探究性也是重要的预测变量（β=0.37），而对于一年级儿童早期数学能力而言，另一个重要的预测变量则是积极性与主动性（β=0.36）。从总体来看，学习品质对大班儿童数学能力的预测作用更强，解释率达71%，对一年级儿童数学能力的预测作用则有所减弱，解释率仅为45%，这表明随着年龄增长学习品质对儿童数学能力的积极支持作用在减弱。

四、讨论

（一）《基于研究的早期数学能力评估工具》对大班和一年级儿童的适用性分析

对儿童数学学习与发展的评估与监测是基础教育质量监测中的重要方面，然而我国儿童数学学习和发展监测指标体系的构建和评估工具的开发仍是一项开创性的工作，[57]尤其是缺乏能够同时测查幼儿园大班和小学一年级儿童早期数学能力的工具。REMA的引入不仅能够帮助教师了解儿童早期数学能力在此过渡阶段的发展状况，还能为研究者未来开发本土化评估工具提供借鉴。本研究运用Rasch模型对REMA进行修订，发现修订后的早期数学能力评估工具具有较好的信效度，能够作为测量大班和一年级儿童数学能力的评估工具。

仔细分析每部分删除项，发现A部分删除的项目为口头数数、倒数、数字排序、比较数字大小等内容，这是因为类似项目较多，且这些项目对于儿童来说比较容易，导致这些项目不能区分儿童之间的能力。相较于A部分，B部分删除项目较多，B部分主要测查儿童空间几何、测量和模式等能力。详细分析，发现几何项目中关于认识形状的任务中，儿童能从具有明显区分的图形中找出目标图形，但若这些图形只有细微的变化，他们就很难辨认出来，如认为钝角三角形不是三角形；在图形组合方面，儿童能用小棒拼出三角形、长方形，但对于儿童来说较难的是用积木拼出相应的图案或用不同的方法拼出同一种图案；在图形比较中，对于儿童来说，比较容易的是给他们形状，他们可以移动匹配，但遇到需要旋转或翻转才能匹配的图形时就比较难；在长度测量方面，儿童能运用感官对物体进行比较，但对于儿童来说比较难的是通过与不同对象的量差异比较来推测出物体量的差异。儿童表现最好的项目是模式，如识别模式中缺失成分、复制或拓展模式，但这些模式内容以重复性内容为主，大多数儿童在5～6岁时就能够发现重复性模式“重复”的本质规律。[58]对删除项目的分析一方面验证了儿童发展轨迹，[59][60]另一方面，也说明当前教师及家长的重心仍在儿童数概念及加减运算的教育上，对空间几何、测量和模式方面的关注度明显不够。这是否需要我们反思：虽然在幼儿园和家庭教育中开展了关于空间、几何、测量、模式等方面的活动，但活动水平较低，对数学核心经验深度认识不足，且这些内容在学前与小学阶段的衔接不够，导致儿童在空间、几何、测量、模式等方面的发展“浅尝辄止”。未来要注重这些方面的教育，再依循我国儿童发展规律对量表进行修正。

（二）大班和一年级儿童早期数学能力和学习品质年龄和性别的差异分析

考察大班和一年级儿童早期数学能力的性别及年级差异，发现一年级儿童早期数学能力显著高于大班儿童，验证了以往的研究。[61][62]这是因为儿童数学能力的发展是一个渐进的过程，随着脑系统（如前额叶皮层背外侧）的成熟以及具体生活经验的丰富而发生变化。另一个可能的原因与本次评估采用的任务范式相关，任务采用教师口头布置的方式，儿童在听到任务后，自主完成，这一过程就需要儿童听力和注意力的参与，而听力与注意力随着年龄增长而越强。对于性别的分析结果显示，男女儿童在早期数学能力总分及分维度上差异不显著，这与有些研究结果是一致的。[63]但有些研究却发现在4～7岁这个阶段，女孩的数学能力比男孩优秀，[64]有的研究却发现男生的数学能力显著高于女生。[65]对于早期数学能力性别差异，未来研究还需进一步扩大样本来验证。

对大班和一年级儿童学习品质进行比较研究，发现性别不存在差异，年级存在差异。但并不是随着儿童年级的增长而呈增长趋势，反而呈负增长，且各分维度发展也不均衡。具体表现在积极性与主动性、专注性与坚持性上，大班儿童显著高于一年级儿童，这与吴（Wu）的研究结果是一致的。[66]幼儿园和小学是两个完全不同的阶段，在制度、课程、教学方法、环境布置、家长角色以及儿童的期望值方面有很大的不同。[67]在幼儿园阶段，游戏是儿童发展最主要的源泉，幼儿在游戏中通过与操作材料的互动获得发展，教师会选择或设计有趣的游戏来吸引儿童的兴趣，儿童会积极主动参与游戏。升入小学，教室结构不一样了，教师对幼儿的期望也不一样了，以儿童为主体的开放性的游戏变成了以目标结果为导向的教学活动，练习为主的教学方式自然会挫伤儿童的兴致，降低儿童的专注性。但在自我调控与解释性、独立性与探究性上，大班和一年级不存在显著差异，前人研究也证实儿童学习品质发展在6～8岁期间趋于稳定，[68]但其考察的是学习品质这一整体维度，学习品质的培养还与课堂教育质量紧密相关，[69]说明在实践教学活动中忽视了对儿童自我调控力、反思与解释、独立性与探究性等学习品质的培养。

（三）大班和一年级儿童早期数学能力和学习品质的关系分析

对大班和一年级儿童的学习品质与早期数学能力进行相关分析发现，学习品质总维度及各分维度与早期数学能力呈显著正相关，这与以往研究结果一致。[70][71]早期数学能力包括程序性能力和概念性能力，概念性能力指的是对程序有效性的理解，程序性能力是执行序列动作来解决问题的能力，[72]需要儿童付出大量的努力和长时间的持续投入。儿童若发现数学任务有趣，就会有更强的探究数学任务的欲望，就会更专注于完成数学任务，就能控制自己的注意、情感和行为，就能坚持完成数学任务，从而获得数学能力的发展。[73][74]进一步考察不同阶段儿童学习品质对早期数学能力的预测作用，在控制年级变量后，发现无论是大班还是一年级儿童，学习品质中预测作用最大的是自我调控与解释性，这与以往的研究结论相一致。[75][76]数学问题解决过程往往需要儿童选择合适的规则，灵活变换规则，[77]说出自己的想法。如儿童在拼图过程中，就会思考选择哪几块图形能拼成目标图形，选择好图形后，会考虑是采用旋转的方法还是翻转的方法以匹配，这个过程伴随着自我对话。随着年级的增长，新的复杂的任务更需要儿童具有良好的自我调控与解释性的能力。同时本研究还发现，对于大班儿童早期数学能力而言，独立性与探究性也是重要的预测变量，这也证实了以往研究。[78]与小学教育不同的是，学前数学教育更注重儿童基于物体的操作和表征，让儿童通过充分的操作、体验和建构了解数的相关概念，[79]这个过程需要儿童具备独立探究的能力。而对于一年级儿童早期数学能力而言，另一个重要的预测变量则是积极性与主动性，这也验证了以往的研究。[80]在一年级，儿童面临着系统教学方式和内容的挑战，若他们在一开始就建立了良好的學习品质，则其之后的数学成就会发展得更好。[81]总体而言，学习品质对早期数学能力的预测作用并没有随着年级的增长而增长，反而呈下降趋势。这一方面与学习品质本身没有随着年级增长而增长有关，另一方面，相较于小学有目的有计划的数学教育，在幼儿园“从游戏中学”的学习方式能使学习品质对儿童数学能力产生更积极的影响。

五、教育建议

（一）注重两个阶段数学教育连贯性，依循儿童数学发展轨迹

近年来，国际上一些研究者、政策制定者、实践者都提倡“学前—三年级一致性”理念，旨在使儿童在学前阶段获得的能力能得到持续发展。[82]这就要求幼儿园大班和小学低年级首先要在教学内容、教学方法上保持连贯，如学前期课程设置要依循儿童数与运算、空间/几何、测量和模式的发展规律设计，小学低年级阶段的课程设置需继续在这几个方面上增加其复杂性；教学方法上，学前期儿童数学能力获得主要是通过对具体材料的操作，小学低年级阶段就要为儿童提供适合发展的学习材料和机会。其次，要依循儿童数学发展轨迹设计适宜活动。目前数学教育重视数与计算能力的培养，对空间/几何、测量、模式等能力培养还浮于表面。因此，不管是幼儿园大班还是小学一年级，要全面深入理解儿童在这些方面的学习发展轨迹，只有这样教师才能设计适宜内容，儿童才能在具体领域深耕细作，才能建构出一条更为清晰的从幼儿园到小学低年级儿童数学学习与发展之路。

（二）多方协作促进学习品质养成，坚持有效衔接与精准实施并重

要充分发挥学习品质对早期数学能力的积极作用。首先，要调动多方力量协同促进学习品质养成。学习品质受家庭、学校、社会的共同影响，早期教育工作者可以通过对每一个影响圈的介入而积极地影响儿童的学习品质，如教师可以有目的地设计能够培养儿童兴趣、投入、坚持性等学习品质的数学课程，建立温暖的、支持性的师幼关系，为儿童提供专注、坚持和全身心投入数学学习的机会，帮助家长提升创设有益家庭学习环境的能力，了解和影响公共政策等。其次，要坚持有效衔接与精准实施。学习品质不仅是学前阶段核心内容，小学低年级也要进一步加强学习品质的培养，要将其纳入到基础教育教学目标和内容中，以目标导向凸显学习品质的核心地位，如改革小学一年级教育教学方式，采用游戏化、生活化等方式实施数学课程，让儿童在新异、有趣的任务中获得发展。同时，还要做到精准定向，学习品质是有年级差异的，比较年级差异的目的是关注学习内容的变化，在幼儿园小班和中班重点是培养儿童在教育活动中的好奇心、兴趣以及在活动中的坚持性，但到了大班，要注重培养其在教育过程中的规则意识，对问题的清晰理解、独立探究事物关系等能力，到了一年级，除了要提升儿童自我控制能力外，还需要为儿童提供积极的支持策略，鼓励并激发儿童在活动中的主动性。

注释：

①表面效度（face validity）即从题目表面是否容易看出出题人的意向和答案倾向。

②同时效度（concurrent validity）即测验分数与同时期可采集到的效标分数之间的相关程度。

参考文献：

[1]DOOLEY T， DUNPHY E， SHIEL G， et al. Mathematics in early childhood and primary education （3～8 years）[J]. Teaching and learning，2014（18）：7-13.

[2]李季湄，冯晓霞.3～6岁儿童学习与发展指南解读[M].北京：人民教育出版社，2013：129-130.

[3]DUNCAN G J， DOWSETT C J， CLAESSENS A， et al. School readiness and later achievement[J]. Developmental psychology，2007， 43（6）：1428-1446.

[4]CLAESSENS A， DUNCAN G， ENGEL M. Kindergarten skills and fifth grade achievement： evidence from the ECLS K[J]. Economics of Education Review，2009，28（4）：415-427.

[5]PAGANI L S， FITZPATRICK C， ARCHAMBAULT I， et al. School readiness and later achievement： a French Canadian replication and extension[J]. Developmental psychology，2010，46（5）：984-994.

[6][13]WATTS T W， DUNCAN G J， SIEGLER R S， et al. Whats past is prologue： relations between early mathematics knowledge and high school achievement[J]. Educational Researcher，2014，43（7）：352-360.

[7]DUNCAN G J， MAGNUSON K. The nature and impact of early achievement skills， attention skills and behavior problems[M]. New York： Russell Sage Foundation，2011：47-70.

[8]周欣.兒童数概念早期发展[M].上海：华东师范大学出版社，2003：57-250.

[9][58]田方. 4～6岁儿童模式能力发展及其干预研究[D].上海：华东师范大学，2021：120-179.

[10]BYRNES J P， WASIK B A. Factors predictive of mathematics achievement in kindergarten， first and third grades： an opportunity propensity analysis[J]. Contemporary Educational Psychology，2009，34（2）：167-183.

[11]GEARY D C. Early foundations for mathematics learning and their relations to learning disabilities[J]. Current directions in psychological science，2013，22（1）：23-27.

[12]JORDAN N C， KAPLAN D， RAMINENI C， et al. Early math matters： kindergarten number competence and later mathematics outcomes[J]. Developmental psychology，2009，45（3）：850-867.

[14]PERRY B， DOCKETT S， HARLEY E. Preschool educators sustained professional development in young childrens mathematics learning[J]. Mathematics Teacher Education and Development，2007（08）：117-134.

[15]SAYERS M， WEST S， LORAINS J， et al. Starting school： a pivotal life transition for children and their families[J]. Family Matters，2012（90）：45-56.

[16][35]DIPERNA J C， LEI P W， REID E E. Kindergarten predictors of mathematical growth in the primary grades： an investigation using the Early Childhood Longitudinal Study Kindergarten cohort[J]. Journal of Educational psychology，2007，99（2）：369-379.

[17][82]MCCORMICK M， MATTERA S， HSUEH J A. Preschool to third grade alignment： what do we know and what are we learning？ Policy Brief[J]. MDRC，2019（3）：1-9.

[18]JENKINS J M， WATTS T W， MAGNUSON K， et al. Do high quality kindergarten and first grade classrooms mitigate preschool fadeout？[J]. Journal of Research on Educational Effectiveness，2018， 11（3）：339-374.

[19]GINSBURG H P， BAROODY A J. Test of early mathematics ability： 3rd ed[M]. Austin，TX：PRO ED，2003：1-4.

[20][65]康丹，周欣，田丽丽，等.《早期儿童数学能力测试（中文版）》对上海市5～6岁儿童的适用性研究[J].幼兒教育，2014（18）：39-45.

[21][46][47]CLEMENTS D H， SARAMA J H， LIU X H. Development of a measure of early mathematics achievement using the rasch model： the Research Based Early Maths Assessment[J]. Educational Psychology，2008，28（4）：457-482.

[22]DONG Y， CLEMENTS D H， DAY HESS C A， et al. Measuring early childhood mathematical cognition： validating and equating two forms of the Research based Early Mathematics Assessment[J]. Journal of Psychoeducational Assessment，2021，39（8）：983-998.

[23]WEILAND C， WOLFE C B， HURWITZ M D， et al. Early mathematics assessment： validation of the short form of a prekindergarten and kindergarten mathematics measure[J]. Educational Psychology，2012，32（3）：311-333.

[24]张迪.Rasch模型在八年级数学学业测试卷质量分析中的应用[J].教育测量与评价，2020（08）：34-41.

[25]NG F F Y， TAMIS LeMonda C， YOSHIKAWA H， et al. Inhibitory control in preschool predicts early math skills in first grade： evidence from an ethnically diverse sample[J]. International Journal of Behavioral Development，2015，39（2）：139-149.

[26]LEE K， BULL R. Developmental changes in working memory， updating and math achievement[J]. Journal of Educational Psychology，2016，108（6）：869-882.

[27]KAGAN S L， MOORE E K， BREDEKAMP S. Reconsidering childrens early development and learning： toward common views and vocabulary[R]. Report of the National Education Goals Panel， Goal1 Technical Planning Group. Washington， DC： U.S. Government Printing Office，1995.

[28]FANTUZZO J， BULOTSKY SHEARER R， MCDERMOTT P A， et al. Investigation of dimensions of social emotional classroom behavior and school readiness for low income urban preschool children[J]. School Psychology Review，2007，36（1）：44-62.

[29]MCWAYNE C M， FANTUZZO J W， MCDERMOTT P A. Preschool competency in context： an investigation of the unique contribution of child competencies to early academic success[J]. Developmental psychology，2004，40（4）：633-645.

[30]STIPEK D， NEWTON S， CHUDGAR A. Learning related behaviors and literacy achievement in elementary school aged children[J]. Early Childhood Research Quarterly，2010，25（3）：385-395.

[31]彭杜宏.兒童早期学习品质的本质内涵、因素结构及学习效应[J].学前教育研究，2020（03）：57-71.

[32]WELSH J A， NIX R L， BLAIR C， et al. The development of cognitive skills and gains in academic school readiness for children from low income families[J]. Journal of educational psychology，2010，102（1）：43.

[33][42][75]张莉，周兢.学前儿童学习品质发展及其对早期语言和数学能力的预测作用[J].全球教育展望，2018，47（05）：113-128.

[34][38][41][48][70][78]徐晶晶，李正清，周欣.学习品质对5～6岁儿童早期数学能力的影响研究[J].幼儿教育，2016（Z3）：69-75.

[36]RAZZA R A， MARTIN A， BROOKS GUNN J. Are approaches to learning in kindergarten associated with academic and social competence similarly？[C]//Child & youth care forum. Springer US，2015，44（6）：757-776.

[37][49][71]王宝华，冯晓霞，肖树娟，等.家庭社会经济地位与儿童学习品质及入学认知准备之间的关系[J].学前教育研究，2010（04）：3-9.

[39]MCCLELLAND M M， CAMERON C E， CONNOR C M D， et al. Links between behavioral regulation and preschoolers literacy， vocabulary， and math skills[J]. Developmental psychology，2007，43（4）：947-959.

[40]PONITZ C C， MCCLELLAND M M， MATTHEWS J S， et al. A structured observation of behavioral self regulation and its contribution to kindergarten outcomes[J]. Developmental psychology，2009，45（3）：605-619.

[43][68]SUNG J， WICKRAMA K A S. Longitudinal relationship between early academic achievement and executive function： mediating role of approaches to learning[J]. Contemporary Educational Psychology，2018（54）：171-183.

[44][66]WU C C. Investigating the effect of the state， stability and change in deep approaches to learning from kindergarten to third grade： a multilevel structural equation modeling indicator specific growth model approach[J]. Frontiers in Psychology，2022（13）：1-13.

[45][62]SUNG J， WICKRAMA K A S. Longitudinal relationship between early academic achievement and executive function： mediating role of approaches to learning[J]. Contemporary Educational Psychology，2018（54）：171-183.

[50]LINACRE J M. Optimizing rating scale category effectiveness[J]. Journal of applied measurement，2002，3（1）：85-106.

[51]杨建原，曾薇.Rasch模型在等级量表设计中的应用[J].中国考试，2012（05）：12-18.

[52]LINACRE J M. What do infit and outfit， mean square and standardized mean？[J]. Rasch Measurement Transactions，2002，16（2）：878-880.

[53]刘勇，李俊平.基于Rasch模型的网络教育学位英语考试试题质量分析：以北京地区为例[J]. 北京邮电大学学报（社会科学版），2022，24（1）：113-120.

[54]刘昊，刘肖岑，冯晓霞.应用 Rasch 模型测试和分析儿童入学准备状态[J].心理科学，2013，36（2）：484-488.

[55]WRIGHT B D， LINACRE J M， GUSTAFSON J E， et al. Reasonable mean square fit values. Rasch measurement transactions[J]. Rasch Measurement Transactions，1994，8（3）：370-371.

[56]赵守盈，何妃霞，刘妍.Rasch模型在学绩测验质量分析中的应用[J].教育研究与实验，2013 （01）：87-91.

[57]周欣，黄瑾，郭力平，等.我国学前儿童数学监测指标体系的构建[J].学前教育研究，2018（10）：12-21.

[59]CLEMENTS D H， WILSON D C， SARAMA J. Young childrens composition of geometric figures： a learning trajectory[M]. New York： Routledge，2012：163-184.

[60]SARAMA J， CLEMENTS D H. Building blocks for young childrens mathematical development[J]. Journal of educational computing research，2002，27（1）：93-110.

[61]LEYVA D， YEOMANS MALDONADO G， WEILAND C， et al. Latino kindergarteners math growth， approaches to learning， and home numeracy practices[J]. Journal of Applied Developmental Psychology，2022（80）：1-10.

[63]MCGINNIS A M. Student behaviors as predictors of later academic achievement： school entry through fifth grade[M]. State College： The Pennsylvania State University，2009，44-59.

[64]AUNOLA K， LESKINEN E， LERKKANEN M K， et al. Developmental dynamics of math performance from preschool to grade 2[J]. Journal of educational psychology，2004，96（4）：699-713.

[67]邬春芹.西方发达国家促进幼小衔接的国际经验[J].比较教育研究，2013，35（2）：28-31+37.

[69]HU B Y， TEO T， NIE Y， et al. Classroom quality and chinese preschool childrens approaches to learning[J]. Learning and individual differences，2017（54）：51-59.

[72]安茜，吳念阳.5～7岁儿童数数概念性知识和程序性知识的发展[J].现代基础教育研究，2020，40（4）：200-208.

[73]COOLAHAN K， FANTUZZO J， MENDEZ J， et al. Preschool peer interactions and readiness to learn： Relationships between classroom peer play and learning behaviors and conduct[J]. Journal of educational psychology，2000，92（3）：458-465.

[74]MCCLELLAND M M， ACOCK A C， MORRISON F J. The impact of kindergarten learning related skills on academic trajectories at the end of elementary school[J]. Early childhood research quarterly，2006，21（4）：471-490.

[76]白潔琼，周晶.早期学习品质与入学认知准备的关系及影响因素研究：元分析的证据[J].教育理论与实践，2022，42（10）：58-63.

[77]BLAIR C， URSACHE A， GREENBERG M， et al. Multiple aspects of self regulation uniquely predict mathematics but not letter word knowledge in the early elementary grades[J]. Developmental psychology，2015，51（4）：459-472.

[79]黄瑾，田方.学前儿童数学学习与发展核心经验[M].南京：南京师范大学，2015：241-323.

[80]DOBBS J， DOCTOROFF G L， FISHER P H， et al. The association between preschool childrens socio emotional functioning and their mathematical skills[J]. Journal of Applied Developmental Psychology，2006，27（2）：97-108.

[81]AUNOLA K， LESKINEN E， NURMI J E. Developmental dynamics between mathematical performance， task motivation， and teachers goals during the transition to primary school[J]. British journal of educational psychology，2006，76（1）：21-40.

The Development of and Relationship between Childrens Mathematical Ability and Approaches to Learning from Preschool to First Grade

YANG Qiong， CAI Jun

（School of Preschool Education， Xian College of Arts and Sciences， Xian 710065 China）

Abstract： The continuous development of mathematical ability and approaches to learning during the period from preschool to first grade is very important to childrens academic achievement at present and in future. 172 children from the top class of kindergarten and the first grade of primary school were taken as the research objects in this study. The results showed that there is age difference in early mathematics ability for children from first grade score significantly higher than children from kindergarten. Childrens approaches to learning dont develop with the growth of grades for children from first grade even show poorer performance than children from kindergarten. Self control and explanation are the most important predictors for both kindergarten and first grade children. Its necessary to understand childrens mathematical learning progress along research based trajectories and pay attention to the connection of mathematical education in the bridging phase from preschool to first grade， and at the same time cultivate childrens approaches to learning through multi party cooperation， especially in primary school， so as to give full play to the positive effect of approaches to learning on early mathematical ability.

Key words： mathematical ability， approaches to learning， connection between preschool and primary education， Rasch model