问题背景探索，示例突破思考

章珣

[摘  要] 抛物线与几何综合题是中考重难点题型，问题兼具“数”与“形”双重特性. 对于其中与几何面积结合紧密的问题，要立足面积公式，通过数形结合来转化条件，构建模型. 文章分析了该类问题的知识背景，结合实例具体探究，并开展解后反思，提出相应的教学建议.

[关键词] 抛物线;三角形;面积;平移转化;模型

背景探索

抛物线与几何图形结合是常见的命题形式，是“数”与“形”融合的典型代表，问题的知识点覆盖广，涉及函数与图像、几何图形的性质特征.

抛物线与几何综合题的构建形式多样，主要以抛物线与直线相交为基础，依托交点构建几何图形，设问形式有求交点坐标，分析图形周长，探究图形面积等. 其中以三角形的属性问题尤为常见，也是抛物线与几何结合的考查核心. 问题突破需要采用数形结合法，以点坐标为关联纽带，通过构建模型将周长和面积问题转化为与线段长或关于点坐标参数的问题.

探究示例

2021年江苏省扬州市的函数压轴题为抛物线与几何的综合，依托交点构建了三角形，问题条件与三角形的面积密切相关，下面笔者进行深入探究.

考题：（2021年江苏省扬州市中考卷第26题）如图1所示，在平面直角坐标系中，二次函数y=x2+bx+c的图像与x轴交于点A（-1，0）和点B（3，0），与y轴交于点C.

（1）b=________，c=________;

（2）若点D在该二次函数的图像上，且S△ABD=2S△ABC，试求点D的坐标;

（3）若P是該二次函数图像上位于x轴上的一点，且S△APC=S△APB，直接写出点P的坐标.

突破第（1）问——待定系数法

该问求二次函数的特征参数，采用待定系数法即可. 已知抛物线上A和B的坐标，将点坐标代入解析式中，可得1-b+c=0，

9+3b+c=0，解得b=-2，

c=-3.

另解，抛物线与x轴的交点为A和B，根据方程根与x轴交点坐标的关系，可直接将二次函数解析式表示为y=（x+1）（x-3），整理后可得y=x2-2x-3，显然b=-2，c=-3.

突破第（2）问——构建面积模型

该问设定点D在二次函数的图像上，条件“S△ABD=2S△ABC”涉及两个三角形的面积关系，其中△ABC为定三角形，其面积可求，故可通过设点D的坐标，构建关于△ABD面积的方程，将问题转化为关于点坐标参数的方程，解方程即可.

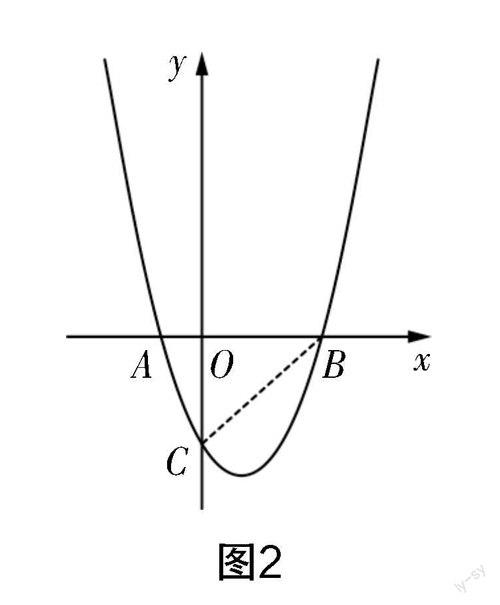
连接BC，如图2所示，由二次函数解析式可求点C（0，-3），则△ABC的面积为S△ABC=×4×3=6，可推得S△ABD=12. 点D位于抛物线上，可设其坐标为（m，m2-2m-3）. 将△ABD视为是以AB为底，D为顶点的三角形，则可将其面积表示为S△ABD=×AB×h，其中h表示点D到AB边的距离，AB=4，所以可将其面积进一步表示为S△ABD=×4×m2-2m-3，则×4×m2-2m-3=12，从而可解得m=1+或m=1-. 当m=1+时，D1（1+，6）;当m=1-时，D2（1-，6）.

突破第（3）问——平行转化建模

该问设定点P在二次函数的图像上，条件“S△APC=S△APB”同样涉及两个三角形的面积关系，属于等面积问题. 不过这两个三角形均含有不确定点P，故无法直接求出其面积. 分析时可将两个三角形视为同底三角形，即△APC和△APB有共同的底AP，结合三角形的面积公式可知，只需确保点B和点C到AP所在直线的距离相等即可. 下面具体推导问题的转化思路，并分析点坐标的位置.

问题转化：“S△APC=S△APB”→点B和C到AP的距离相等→BC∥AP.

位置分析：BC∥AP→点P位于抛物线x轴的上方.

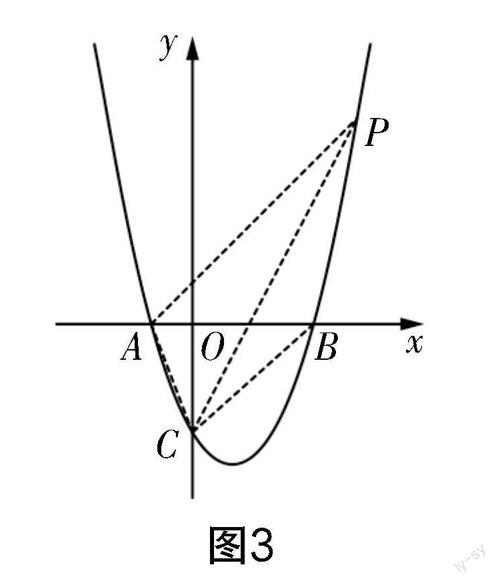
根据上述分析，可知点P位于x轴的上方，可设点P（n，n2-2n-3），故n2-2n-3>0，可解得n<-1或n>3. 当n<-1，此时点P位于点A的左侧，显然无法构建AP，使得BC∥AP，不成立. 当n>3，此时点P位于点B的右侧，如图3所示. 可设直线BC的解析式为y=kx+p，结合点B和C的坐标可得k=1，p= -3，即直线BC的解析式为y=x-3. 设直线AP的解析式为y=k1x+q，因为BC∥AP，则k1=k=1，将点A（-1，0）代入其中，可得y=x+1，将点P（n，n2-2n-3）代入其中，可得n2-2n-3=n+1，可解得n=4或n=-1（舍去），所以可得点P的坐标为（4，5）.

问题思考

上述对考题的思路构建过程进行了深入探究，后两问为核心之问，均与三角形的面积相关. 但从问题的构建思路来看，其转化过程、模型构建等环节有着较大的差异. 下面笔者针对两个核心问题进行深度思考.

问题1  后两问涉及三角形面积关系，思路构建有较大差异的原因是什么？

第（2）问条件“S△ABD=2S△ABC”中，涉及△ABD和△ABC，其中点D的位置不确定，造成△ABC为定三角形，而△ABD为“动三角形”，从而可直接求出三角形的面积. 而第（3）问条件“S△APC=S△APB”中，不确定点P位于两个三角形中，这就造成两三角形的面积不可求，只可结合面积公式来推测顶点的位置关系.

问题2  第（2）问和第（3）问均求顶点坐标，造成解个数不同的原因是什么？

结合“平行线之间的距离相等”可知，在确定三角形的底边和顶点的情形下，理论上满足条件的点有两个，且两点的连线与底边所在直线相平行. 而在第（2）问中，底边BC与x轴重合，故满足条件的顶点D1和D2的连线与x轴平行，即两点的纵坐标相等，由于两点位于抛物线上，则两点关于抛物线的对称轴对称. 在第（3）问中，同样通过平行来确定点坐标，但AP是作为三角形底边来构建的，且点A为定点，位于抛物线上，故通过作平行线只可求得一点.

问题3  对于第（3）问的等面积关系，可从哪些角度来变式？

变式1：若将其中点A的坐标变更为（-2，0），则满足条件的点P有几个？

分析：基于上述问题2的探究，可知满足条件的点P有两个. 从几何视角来看，相當于将原题目中的直线AP向左平移1个单位长度.

变式2：若P是该二次函数图像上位于x轴上的一点，且S△APC=S△APB，是否可求出四边形ACBP的面积？

分析：四边形ACBP为一般的四边形，确定其坐标后，可采用面积割补的方法求其面积，可将其表示为S四边形ACBP =S△ABP +S△ABC=×AB×yP -yC，代入线段长和点坐标即可求解.

教学建议

1. 关注问题考点，探究知识本质

抛物线与几何综合属于重难点题型，问题涵盖了众多的知识考点，问题的构建形式较为复杂，实际突破过程需要学生充分把握知识考点，深入探究问题本质. 以上述第（2）问为例，给出面积关系求点坐标，主要考查面积转化、模型构建，以及函数背景下几何推理. 从问题本质来看，实则为面积方程问题，即根据几何面积构建关于坐标参数的方程. 在实际教学中，建议教师引导学生分步审题：第一步，梳理题干信息，归纳知识考点;第二步，解析问题条件，深度转化思考;第三步，回归教材知识，探究问题本质.

2. 把握核心解法，生成解题策略

从问题属性来看，可将上述问题归为函数图像中的面积关系问题，问题具有“数”“形”融合的特性，故数形结合是该类问题突破的核心解法，该方法体现在读图审题、条件转化、模型构建、推理计算等多个过程中. 以上述考题的第（3）为例，在探究等面积关系条件下顶点坐标时，充分结合数形结合的方法，基于顶点属性构建面积模型，通过平行特性来确定顶点坐标，利用点代法来推理计算. 实际教学中，教师要引导学生深刻理解数形结合的方法内涵，掌握数形结合解析问题的核心步骤，即首先结合图像理解题意，根据图像的特征挖掘隐含条件，然后通过解方程、求函数解、分析函数性质等方法完成推理计算.

3. 深度思考问题，合理变式探究

“解后反思”是解题教学的重要环节，在该环节中教师可以全面审视问题，反思解法，形成类型问题的解析策略. 以上述考题反思为例，笔者对后两问的构建思路、问题的解、变式方向进行了探究，从顶点属性、模型构建、平移转化等视角进行了深入思考，所总结的解题经验对于后续类型题的探究十分有利. 实际上抛物线背景下的几何面积问题十分常见，并形成了面积比值转化、面积存在性、面积最值等多类型问题，但问题突破的方法策略是一致的，故开展解后反思极为重要. 实际教学中，建议教师引导学生立足问题反思解法，利用解析方法探索问题特征，给学生留足思考空间，让学生在思维碰撞中获得能力提升.