基于栈式结构的深度极限学习机

董 帅，申 情，张雄涛

(1.湖州师范学院 信息工程学院，浙江 湖州 313000；2.湖州学院 理工学院，浙江 湖州 313000)

近年来，深度学习在理论研究和实际应用中取得了突破性进展[1].深度网络通过不断堆叠网络单元来模拟大脑的层次化认知规律，具备出色的模型性能.Hinton指出，拥有大量隐层的神经网络具有优异的特征学习能力[2].随着数据计算能力和存储容量的显著提升，深度网络如CNN[3]、DBN[4]在多个应用领域得到广泛运用.但此类深度算法大多为基于梯度的算法，在机器学习任务中往往会受限于冗长的训练过程，也常常涉及复杂的网络结构和繁多的参数设置等一系列问题.而极限学习机(Extreme Learning Machine,ELM)[5-6]因结构简单、学习速度极快、人工代价小和泛化能力良好，在生物医学、计算机视觉、故障诊断等领域得到广泛应用[7].区别于深度网络，ELM只包含单个隐含层，且隐层参数通过随机初始化产生，输出权值由伪逆计算求解得出.但ELM仍然无法规避浅层网络的局限性，难以发掘原始数据中所承载的大量隐含价值，从而导致重要信息流失.

Kasun等将自编码器与极限学习机结合，提出基于ELM自编码器(ELM AutoEncoder,ELM-AE)的深层模型，并在深层架构中引入ELM-AE作为基本构建单元[8].Zhou等针对大规模的复杂数据，提出一种堆叠结构的深度ELM模型，其以串联方式组合多个小规模ELM网络[9].将数据中的有用信息进行有效融合，这对高性能的机器学习模型至关重要[10].但上述深度ELM模型未能充分利用层间所学的知识.与现有的深度集成方法不同[11-12]，本文基于ELM提出一种易于实施、快速训练的深度栈式分类器.

1 基础知识

1.1 极限学习机理论

在ELM中，原始输入被映射到ELM的随机特征空间中，最后通过求解一个线性系统得到输出.相比其他机器学习算法，ELM能以更快的速度、更优的泛化性能、更简洁的网络架构和更少的人工干预完成学习任务.ELM网络结构如图1所示.

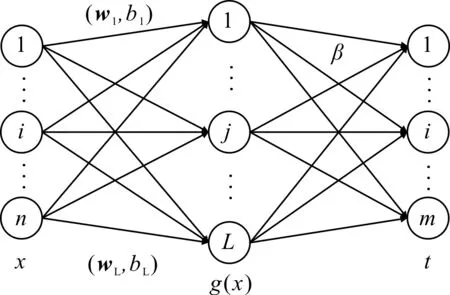
图1 ELM网络结构Fig.1 The network architecture of ELM

对给定的N个不同的输入样本，xi=[xi1,xi2,…,xin]T∈Rn，ti=[ti1,ti2,…,tim]T∈Rm，g(·)为激活函数，n为输入层节点数，L为隐层节点数，m为输出层节点数.ELM网络的数学模型可表示为：

(1)

其中，wi=[wi1,wi2,…,win]T为输入权重，βi=[βi1,βi2,…,βim]T为输出权重，bi为第i个神经元阈值.整个模型可改写为矩阵的紧凑形式：

Hβ=T.

(2)

其中，H为隐含层的输出矩阵，在矩阵中第i列的值为隐含层第i个神经元的对应输出；β和T分别为输出权值矩阵和ELM的期望标签矩阵.

上述线性系统的最小范数最小二乘解为：

(3)

其中，H†为H的广义逆矩阵.

1.2 dropout思想

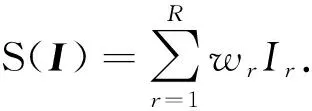
(4)

其中，N为所有子网络的集合.

2 新型深度栈式ELM模型

2.1 FT-DSELM网络结构

本文提出的新型深度栈式网络FT-DSELM，在维持经典ELM分类器优秀特性的基础上，利用堆叠泛化理论[15-17]实现深度学习.栈式结构兼具ELM的实时响应能力和深度网络的深度表征能力，并以ELM分类器作为基础模块，大大缩短了深度网络的训练时间，降低了深度模型的计算复杂度.深度学习理论与极限学习机结合而成的栈式ELM架构，不仅能加快深度模型的学习进程，还能有效探索数据承载的丰富知识，并改善原始特征表达.与现有的基于深层堆叠的ELM方法不同[18-19]，FT-DSELM不仅保持了原始ELM的网络架构，而且在更新数据空间的同时不会使原始数据的结构发生过多改变.

每个子ELM分类器引入dropout思想，降低了隐层规模，加速了训练过程.若ELM的隐节点设置不当，则会导致资源消耗巨大、过拟合等问题.dropout有着强大的理论和生物学基础，在理论上被认为是自适应正则化，已被证明是一种训练神经网络的有效途径.因此，根据dropout理论[20]，可利用防止特征检测器的协同适应来缓解过度拟合问题.首先，初始化一个规模相对较大的ELM网络，通过dropout随机剔除若干个隐层节点，从而在一定程度上减少此类过拟合问题；然后，在构建每个子ELM分类器时，根据均匀分布生成L维的0-1向量，并按照生成的0-1向量对隐层节点进行删除.在集成学习思想中，分类器集成的关键是基础分类器的多样性表现[21].当多个基础分类器在部分样本分类任务上存在误差多样性时，多个基础模块间往往能够优劣互补.经典的ELM隐层参数通过随机初始化生成，而dropout会使每个子ELM分类器的隐层各不相同，从而有效地增强栈式模型的集成多样性.

图2为深度栈式ELM知识增强的总体框架.假定FT-DSELM的最终深度(子模块数目)为D，知识生成过程阐释如下.在起始层的子模块中，样本实际输出矩阵的形式可表示为：

(5)

其中，m为输出节点数，N为样本数.

从起始层的栈层开始，执行ELM的学习流程，生成第一层子模块的决策信息；将该决策信息视作辅助的增强知识，并扩充至原始数据集，从而生成增强数据；融合后的增强数据为更高层子模块提供输入.

图2 深度栈式网络框架Fig.2 The architecture of the deep stacking network

下面阐述第d(1

与首个子分类器中的工作流程相同，求出实际输出矩阵Yd.根据式(3)，该矩阵计算和矩阵可表示为：

(6)

(7)

为方便起见，定义矩阵P1为原始输入，并将其作为起始层的输入数据；Ad为第d个子分类器学习到的增强特征；D为最终栈式结构中子分类器的个数.从起始层的子模块到最终决策级别的子模块，各个栈层输入数据的规则可表示为：

P1=P1,P2=[P1|A1], ⋮Pd=[P1|Ad-1], ⋮

PD=[P1|AD-1].

(8)

考虑到当前子模块的测试效果优于紧邻的前一子模块，在d层后将继续堆叠更多子模块.而第D层子模块的建立，标志着新型深度栈式网络构建的完成.

FT-DSELM是以ELM作为基本模块构建的一种快速训练，且与源数据空间始终保持一致的栈式结构.高层模块将从低层学得的知识作为新的特征，并将其添加到原始特征中，以强化网络的分类性能.传统的深度网络模型，在多重隐含层上所抽象出的中间特征与原始数据的特征并不相同，通常很难去通俗地解释中间特征的意义.但在本文的栈式结构中，每一层栈层的输入都基于原始空间，因此源数据的全部特征信息得以完整保留.栈式结构中的数据空间始终是由原始特征信息和增强特征信息构成的，因而具有明确的物理意义.根据堆叠泛化原理，对任何作用在该增强数据集上的子分类器，其分类性能普遍高于原始数据集的结果.增强特征激发了深度栈式ELM更强的分类潜能.利用更新样本空间方式，前层的学习结果对后续层的学习可起到良好的引导作用.FT-DSELM在后续多模块中将原始输入空间的流形分离，以堆叠的方式更好地实现样本的线性可分.

2.2 算法流程

本文提出的FT-DSELM学习算法见表1.

表1 FT-DSELM学习算法

3 实验与分析

3.1 实验数据集

为验证新型深度栈式ELM的有效性，本文通过数值实验进行算法的性能比较.实验数据集选自加州大学欧文分校的UCI数据库，见表2.表2涵盖了数据集的样本数目、特征维度和类别数.

表2 所用数据集的详细信息

本实验采用的数据集需要归一化处理.在各个数据集中随机选取80%的样本作为训练集，剩余的作为测试集.实验所用的性能评估指标包括分类准确率和执行时间.所有实验均在MATLAB 2019a软件平台上完成，电脑配置为64位的Windows 10操作系统，CPU配置为Intel(R) Core(TM) i5-9400 2.90 GHz，内存为8 GB.

3.2 参数设置

本文选取主流的深度学习算法和集成学习算法作为对比算法，其中包括DBN、SAE、Adaboost和Bagging.两种深度算法都从DeepLearnToolbox工具箱中直接调用，代码通过MATLAB实现.在小规模数据集上，深度算法的隐层单元数取值范围为[10∶10∶40]，Epoch和Batchsize分别在[10∶10∶40]和[20∶10∶50]范围内进行搜索.在大规模数据集上，深度算法的隐层单元数取值范围为[30∶10∶50]，Epoch和Batchsize分别在[40∶10∶60]和[60∶10∶100]范围内寻找最佳参数.两种集成学习算法都需要考虑子分类器的数量.针对前5个数据集通过网格搜索在[2∶1∶6]中选取参数，剩余的数据集通过网格搜索从[10∶1∶20]中确定参数.本文提出的栈式结构深度设置为D=6.

3.3 结果分析

对比经典的深度算法DBN、SAE，集成算法Adaboost、Bagging，以及FT-DSELM的分类精度和标准差，结果见表3.FT-DSELM知识增强后的分类性能见表4.

表3 所有对比算法在UCI数据集上的分类准确率

表4 FT-DSELM知识经增强后的分类性能

实验结果表明：FT-DSELM通过知识增强策略，可在大部分数据集上获得良好的分类表现；在CHE、NUR数据集上，深度栈式ELM的表现不如DBN，这也证实了传统的深度网络之强大.结合表4可知：在NUR数据集上，FT-DSELM具有较强的性能，且很好地提炼了原始数据中的知识；在RIN和ONL数据集上，FT-DSELM的分类表现逊色于深度方法SAE；在ONL和CHE数据集上，相比浅层ELM，FT-DSELM具有显著的改善效果，基本可以获得与传统深度算法持平的性能；在RIN和NUR数据集上，尽管知识的增量学习策略是有效的，但新型的栈式结构与传统的深度算法间仍存在一定的性能差距.

图3为FT-DSELM的训练和测试准确率及隐层单元数目，其中ELM的隐层单元数目通过寻优确定.下面以数据集MON为例，研究FT-DSELM随着增强特征逐级融合而产生的性能变化.

MON是一个包含7个特征的数据集，在第一层子ELM中的输入即为7维的源空间输入.除首个子分类器外，其余所有子分类器的输入构成均基于源输入空间和前一层的增强知识.在MON数据集上，首个子分类器的测试准确率为78.07%，经过多重的知识增强后，之后几层的分类准确率分别为 80.37%、81.42%、81.97%、82.35%、82.60%.在相邻模块间，测试性能的改善程度分别为2.3%、1.05%、0.55%、0.38%、0.25%.可见，在堆叠一定层数后，增益逐渐降低至较低水平.考虑之后堆叠栈层的性能增益明显过低，因此不再执行更多的特征融合操作.FT-DSELM起始层的分类准确率不如Bagging算法，但在经过栈式结构的逐层特征融合和知识增强后，其最终的分类精度优于Bagging集成算法.

图3 深度栈式网络在数据集上的准确率和隐层单元数Fig.3 Comparison of FT-DSELM results for accuracy and hidden units for each dataset

一般而言，FT-DSELM消耗的时间代价会随着栈层数目的增加而不断增加.随着子模块数量的增多，准确率不断提升，但当增强效果相对饱和、准确率非常接近时，再持续引入子模块，性能反而可能下降.由此表明，准确率与时间代价之间需要取得良好的折衷.这也是本文栈式结构设置为6层的原因.

3种深度算法DBN、SAE和FT-DSELM的时间消耗如图4所示.实验结果表明，FT-DSELM为深度学习提供了一种有效的快速训练深度分类器.基于浅层ELM，知识增强策略可充分利用多模块的分类知识，有效地改善FT-DSELM的分类性能.在保证一定准确率的基础上，本文提出的方法有利于缩短算法的执行时间，加快隐含知识的深层学习.因此，FT-DSELM的训练速度远快于传统的基于迭代微调的深度算法，并具有极佳的时间效率.

图4 3种深度算法在时间开销上的对比Fig.4 Comparison of three deep algorithms in time cost

4 结 语

本文提出了一种基于快速训练的深度栈式极限学习机.利用栈式泛化原理深度堆叠多重ELM子分类器，在栈式结构中不断重构输入空间.重构的数据空间由两部分组成：原始特征信息和增强特征信息.两种信息有助于解开源输入空间的流形结构.在每一层栈层中，通过dropout改善栈式架构的集成多样性来降低每个子ELM的隐层规模.基于UCI数据集的实验表明，FT-DSELM是一种高效的深度分类器，其训练速度远快于传统的深度模型，在保证分类精度的基础上，能够以极快的速度挖掘原始数据中的隐含知识，获得较好的分类性能.如何实现FT-DSELM栈式结构的并行化，并将其应用到实际的大规模数据问题中，这是下一步需要研究的重点.