Statistical Properties of Cosine-Gaussian Schell-model Vortex Beams in Free Space and Oceanic Turbulence
2022-05-30KEJiachenWANGMinjieXUZhengkangCHENRuichaoMAOYonghua
KE Jiachen, WANG Minjie, XU Zhengkang, CHEN Ruichao, MAO Yonghua
(School of Science, Huzhou University, Huzhou 313000, China)
Abstract: In this paper, the analytical expressions for the cross-spectral density of Cosine-Gaussian Schell-model Vortex (CGSMV) beams propagating through oceanic turbulence are derived by using the extended Huygens-Fresnel principle. Combined with the spatial power spectrum of oceanic turbulence, the evolution behavior of CGSMV beams through oceanic turbulence is studied in detail by numerical simulation. It is shown that when the beams propagate in free space, the spectral density distribution gradually split into four beams and each individual lobe remains as the dark core at the short propagation distance. With the propagation distance increases, the dark core will gradually disappear. However, when the beams propagate in oceanic turbulence, both spectral density distribution and spectral degree of coherence distribution will be destroyed by turbulence effect.
Keywords: Schell-model beams; vortex beams; oceanic turbulence; propagation characteristics
0 Introduction
Vortex is a special structure widely existing in various physical media. It is found not only in the micro-structure of superfluids and superconductors, but also in natural phenomena such as meteorological vortices and water flow vortices. In the optical field, optical vortices are formed when the phase carries singularities[1-2]. As a unique light field, vortex beams have important potential applications in the fields of free space optical communication[3], optical micro-manipulation[4-5], optical measurement[6-7], super-resolution imaging[8-9]and so on. At present, high-order Laguerre-Gaussian (LG) beams are common and typical vortex beams. In addition, due to the needs of research, scholars have also proposed various specific beam models to describe vortex beams, such as Gaussian-like vortex beams[10], high-order Bessel beams[11], anomalous vortex beams[12]and perfect vortex beams[13-14].
On the other hand, coherence is an extremely important properties which has been widely studied in the past decades[15-16]. Laser beam with low spatial coherence is named partially coherent beam. Partially coherent beams have broad application prospects in many fields because of their rich physical properties, research on it is an important branch in the optical field. In recent years, thanks to the early research work of F. Gori and co-workers[17-18], a large number of partially coherent beam models with non-conventional correlation functions have been proposed[19-20]. Compared with conventional partially coherent beams, the non-conventional partially coherent beams have unique characteristics such as self splitting, self focusing and self shaping.
Since Gori et al used the incoherent superposition of a series of coherent Laguerre Gaussian modes to form a partially coherent vortex beam with helicoidal modes, the research scope of vortex beam has been extended from fully coherent vortex beam to partially coherent vortex beam[21]. Partially coherent vortex beam displays a unique properties, e.g. correlation singularity[22-23]. Previously, scholars were more focused on the conventional partially coherent vortex beams[24-26]. In the past several years, by introducing a vortex phase, partially coherent vortex beams with non-conventional correlation functions have been reported, including multi-Gaussian Schell-model vortex beams[27-29], Laguerre-Gaussian Schell-model vortex beam[30], sinc Schell-model vortex beam[31].
In the paper, we will introduce a new kind of non-conventional partially coherent vortex beam whose correlation function is of cosine-Gaussian distribution named cosine-Gaussian Schell-model vortex (CGSMV) beam. Based on the extended Huygens-Fresnel principle, we will derive the analytical expression for the cross-spectral density function of the CGSMV beams propagating in oceanic turbulence and analyze the evolution properties of the spectral density and the degree of coherence by numerical simulation. Some useful and interesting results in the paper are found.
1 Propagation laws for the CGSMV beams in oceanic turbulence

(1)
whereσ0is the rms source width,δ0is the rms correlation width,nis arbitrary real constants.
In Cartesian coordinates system, the field distribution of a vortex beam at the source planez=0 is expressed as[34]
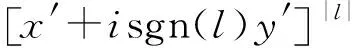
(2)
whereu(ρ′) represents the profile of the background beam envelope, sgn(·) is the sign function, andldenotes the topological charge.
Assumeu(ρ′) takes a cosine-Gaussian Schell-model form, the CSD function of CGSMV beams at the source plane can be expressed as follows
(3)
For simplicity, the topological chargelis adopted ±1 in the following.
By using the extended Huygens-Fresnel principle, the cross-spectral density function of a CGSMV beam through oceanic turbulence at the receiver planezis described as[35],
(4)
whereρ1=(x1,y1) andρ2=(x2,y2) are two arbitrary transverse position vectors at thezplane,k=2π/λis the optical wave number,φdenotes the complex phase perturbation due to the random distribution of the medium’s refractive index, 〈…〉Mdenotes averaging over the ensemble of the turbulent medium. According to [35], the last term in the integrand of Eq. (4) can be shown by the expression
(5)
whereΦn(κ) is the spatial power spectrum of refractive index fluctuations,κis the magnitude of the spatial wave number.
When the eddy thermal diffusivity and the diffusion of salt are assumed to be equal, the power spectrum of the homogeneous and isotropic oceanic water can be given by the expression[36-38]
(6)

On substituting from Eq. (3) and Eq. (5) into Eq. (4) and after straight forward calculations, the cross-spectral density of the CGSMV beam is derived as
(7)
Where
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
Using of the symmetry,by±,dy±andgy±can be obtained frombx±,dx±andgx±by replacingx1andx2withy1andy2, respectively.
Substituting Eq. (6) and parameters ofAT,AS,ATSandδinto Eq. (12), it can be simplified to
(19)
According to Eq. (7), we can investigate the properties of the spectral densitySand the degree of coherenceμof the CGSMV beams on propagation, which are given by [15] and [16]
S(ρ,z)=W(ρ,ρ,z),
(20)
(21)

Fig.1 Evolution of normalized spectral intensity of a CGSMV beam propagating in free space

Fig.2 Evolution of normalized spectral intensity of a CGSMV beam propagating in oceanic turbulence
2 Numerical examples of a CGSMV beam in free space and oceanic turbulence
In this section, we will analyze the evolution properties of CGSMV beams propagating through oceanic turbulence by a set of numerical examples. The numerical calculation parameters of the source beam are set as follows:σ0=5 mm,δ0=2 mm,n=3,λ=632.8 nm,l=+1, unless other values are specified in Figure captions.



Fig.3 The normalized spectral intensity of a CGSMV beam propagating through oceanic turbulence at propagation distance z=40 m with different values of w (ε=10-2, χT=10-8)

Fig.4 The normalized spectral intensity of a CGSMV beam propagating through oceanic turbulence at propagation distance z=40 m with different values of χT (ε=10-2, w=-4)

Fig.5 The normalized spectral intensity of a CGSMV beam propagating through oceanic turbulence at propagation distance z=40 m with different values of ε (w=-4, χT=10-8)

Finally, to investigate the influence of oceanic turbulence parameters on the spectral degree of coherence, we illustrate the absolute value of spectral degree of coherence of the CGSMV beams through oceanic turbulence at propagation distancesz=50 m for different values ofω,χTandεin Fig.7. It can be clear from Fig.7 that the degree of coherence profiles can weaken the oscillations asωandχTincrease orεdecrease.

Fig.6 Modulus of spectral degree of coherence μ of a CGSMV beam propagating in free space (a)~(c) and oceanic turbulence (d)~(f) at several propagation distances z

Fig.7 Evolutions of the degree of coherence for a CGSMV beam propagating in oceanic turbulence at propagation distances z=50 m for different values of turbulent parameters
3 Conclusion
As a summary, we have introduced a new kind of partially coherent vortex beam named CGSMV beam as an extension of CGSM beam. The analytical expression for the CSD function of the CGSMV beams propagating through oceanic turbulence has been derived by using the extended Huygens-Fresnel principle. Then, according to CSD function deduce the expressions for the spectral density and the spectral degree of coherence and analyze the statistical properties by numerical simulation. It is shown that the spectral density distribution of the CGSMV beams propagating in free space gradually split into four beams and each individual lobe remains as the dark core at the short propagation distance. Due to the effect of oceanic turbulence, the lobe has no have dark core, and the lobe gradually will be destroyed and eventually transformed into a Gaussian distribution when it passes at sufficiently large distances or the oceanic turbulence is strong enough. In addition, The spectral degree of coherence is also destroyed by the turbulence. Our work may be useful in some applications, such as the optical micro-manipulation.
