基于复合扰动观测器的自主地面车辆数据驱动轨迹跟踪控制
2022-05-30张鹏飞陈启源杨婷婷
张鹏飞,陈启源,杨婷婷
(湖州师范学院 工学院,浙江 湖州 313000)
0 引 言
随着人们对安全性、准确性和效率需求的提高,自主地面车辆(Autonomous Ground Vehicle, AGV)的轨迹跟踪控制在民用和工业中的作用更加明显,例如自动导引、平台补给、扫雷等[1].轨迹跟踪控制的关键在于其能够精确、可靠地控制车辆,跟踪期望轨.但因其受强非线性、不确定性、扰动和机械结构的限制,轨迹跟踪控制问题具有挑战性.
对轨迹跟踪的研究已有许多成果.文献[2]基于自抗扰非奇异终端滑模策略(Nonsingular Terminal Sliding Mode-Active Disturbance Rejection Control, NTSM-ADRC),设计了一种AGV轨迹跟踪滑模控制器.该控制器虽然能有效解决不确定性系统问题,且易于实现,但观测器误差收敛的截止时间不精确.与上述方法相比,有限时间控制方法不仅具有更快的收敛速度,还具有更好的抗干扰性和对不确定性的鲁棒性[3].该特性在扰动观测器上可反映为对扰动变化较强的适应性[4].进一步地,固定时间方法可保证截止时间与初始条件无关[5].然而,当系统动力学模型完全未知时,系统的控制模型则由模型与数据混合驱动转换为完全数据驱动控制.此时,常规的扰动观测器(如自抗扰、有限时间、固定时间扰动观测器),因未知动态与扰动较大,容易造成观测器失效问题.因此,如何设计数据驱动控制器,以保证AGV固定时间轨迹跟踪控制,仍然需要进一步研究.
本研究设计一种基于复合扰动观测器的数据驱动方法,在动力学模型未知的情况下,保证AGV跟踪参考轨迹运动.其主要贡献有三个方面:
(1)提出一种基于视线法(Line Of Sight, LOS)的新型时变制导方法,通过引入时变参数来处理横向漂移引起的非线性项,从而设计出AGV运动学层面的航向与速度制导方法.
(2)考虑在动力学模型完全未知的情况下,使用扰动观测器等常规估计方法.此法在采样和执行器间隔较大的情况下,由于扰动变化过大,易造成观测器失准问题.为此,在固定时间的观测器估计前做出预补偿,引入时变延时估计方法[7],组成复合扰动观测器.将未知量缩小在相邻采样的差值区间内,以减小初始误差.
(3)结合提出的时变制导律和复合扰动观测器,得到基于复合观测器的轨迹跟踪控制律.
1 系统建模与控制目标
本研究的AGV系统可通过位置与方向来描述.根据文献[2],AGV的动力学模型可描述为:
(1)
其中,vx、vy、wr分别为在惯性坐标下车辆的纵向速度、横向速度与方向角,参数m为车辆质量,Fyf、Fyr分别为前后车轮轴的等效横向力,Lf、Lr分别为车辆重心到前后车轮轴的距离,Iz为转动惯量.在转向角足够小的基础上,前后轮的侧向力被线性化为[2]:
(2)
其中,Cf、Cr为前后车轮轴的等效横向刚度,δf为前轮转向角,af、ar为前后轮侧倾角,β为车辆侧倾角.结合式(1)和式(2),本文考虑的AGV非线性模型可描述为:
(3)
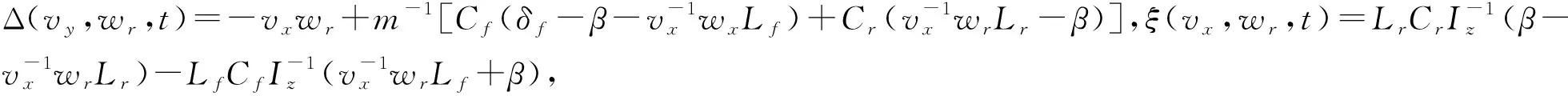
(4)
其中,xref、yref分别为纵向和横向的期望位置,vx,ref、vy,ref分别为纵向和横向的期望速度,φref、wref分别为车辆期望的方向角和方向角速度.分析系统(3),通过构造期望方向角φref,将轨迹跟踪问题转化为方向角跟踪控制问题[2],以满足φ→φref.定义位置误差xe=x-xref、ye=y-yref、φe=φ-φref,从而可得位置误差的导数为:
(5)
本文的目标为:考虑动力学模型Δ(vy,wr,t)与ξ(vx,wr,t)完全未知的情况,设计数据驱动控制律,以实现轨迹跟踪误差系统(5)的镇定控制.
2 制导律设计
通过模型变换方法有效降低控制器设计的复杂性.定义坐标变换为:
z1=xecosφ+yesinφ,z2=-xesinφ+yecosφ.
(6)
状态[z1,z2]的动力学为:
(7)
本文未采用极坐标变换方法.其原因是,在极坐标变换法的坐标变换中存在奇异点问题,即在目标点处具有奇异性.尽管该方法在理论上存在问题,但在实验中效果良好.
引理1[2]系统[z1,z2]的稳定性等价于系统(5)中子系统[xe,ye]的稳定性.

(8)

在实际应用中,纵向速度vx是足够大的,从而导致|vx|>|fz2|.此时,Δ的取值不受限制.将φ-φref代入式(7),解得[z1,z2]的导数为:
(9)
因此,要使车辆严格遵循参考轨迹,只需设计速度vx就可以镇定z1.
引理3若方向角φ与纵向速度vx满足条件:
(10)
其中,参数κu>0,则式(7)中的状态[z1,z2]收敛于零.
证明把式(10)代入式(7),可得z1与z2的动力学状态为:
(11)
显然,当t→∞时,状态z1和z2的收敛为零.
3 控制器与观测器设计
3.1 复合扰动观测器
vx的动力学控制是一阶系统的控制,相对简单.本文假设vx已实现闭环控制,重点研究AGV方向角φ的控制问题.而在无动力学模型信息的情况下设计数据驱动控制律,须使用扰动观测器对不确定性进行估计.由于系统模型完全未知,所以Δ(vy,wr,t)和ξ(vx,wr,t)相对较大,若执行器和采样间隔过大,则对观测器有失准风险,不利于实际使用.本文引入时间延时估计方法[11],对系统误差进行预补偿.当采样时间的间隔L足够小时,可利用上一时刻已知的状态响应和控制输出,估算系统此时刻的状态.对预补偿后的剩余误差,应达到对系统误差的精确估计.
将AGV所需的方向角定义为:
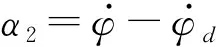
(12)
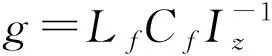
(13)
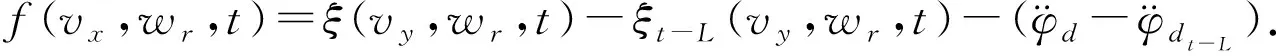
为进一步处理估计误差,假设采样时间L足够小,使得f(vx,wr,t)的变化速度较小,其满足:
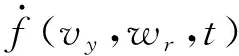
若能引入扰动观测器,就可以对剩余误差进行进一步的精确估计.为方便后续分析,引入固定时间控制定义[12].
定义1考虑系统
(14)
其中,x∈Rn为系统状态变量,g:R+×Rn为非线性函数.如果系统是全局渐近稳定的,且任意解x(t,x0)在某个固定时间到达平衡,则系统(14)被称为在固定时间内是稳定的,即x(t,x0)=0,∀t≥T(x0),其中T:Rn→R+∪{0}为截止时间.
(15)

引理4系统(12)在假设1的前提下,通过观测器(15)可以在固定的时间内估计f(vx,wr,t).
证明证明过程参考文献[8]的定理3.
3.2 控制律设计
基于固定时间观测器设计轨迹跟踪控制策略,考虑上述扰动观测器(15),系统(12)可描述为二阶非线性形式:
(16)

(17)
其中,κ1、κ2为可选择的正常数.将式(17)代入式(16),可得:
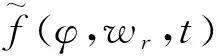
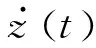
定理1考虑系统(3),在假设1成立且vx满足式(15)的情况下,控制律(17)可保证AGV在动力学模型和外部扰动未知的条件下实现轨迹跟踪控制.
证明由引理4可知,控制律(17)可保证系统(16)的固定时间稳定.由引理3可知,控制律(17)可保证AGV实现轨迹跟踪控制.
根据定理1,控制律(17)可在模型未知和外部扰动不确定的条件下,实现自主车辆数据驱动轨迹跟踪控制.
4 仿 真
为验证该方法的有效性,采用Matlab平台模拟轨迹跟踪模型,其模型是由文献[2]给出的一般AGV模型.在模拟仿真中,应用制导律(8)、复合扰动观测器(15)和控制律(17).设定AGV的初始条件为:
[x(0),y(0),φ(0),vx(0),vy(0),wr(0)]=[4.97/m,6.8/m,0/rad,0/m·s-1,0/m·s-1,0/rad·s-1],
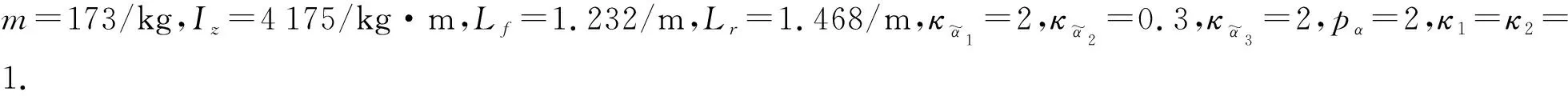
为比较本文提出的方法的有效性,分别将跟踪性能、控制信号输入情况与文献[4]提出的方法进行比较.图1选择的参考轨迹Ⅰ为:
vx=3/m,φd=0.3sin(0.1×t)/rad.
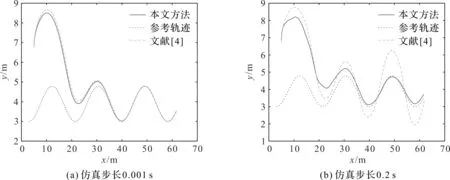
图1 参考轨迹Ⅰ跟踪的比较Fig.1 Reference trajectory tracking comparison Ⅰ
实验结果显示,尽管在步长为 0.01 s 时,二者的跟踪性能相似,但为更加真实地展现控制方法在实际中的表现,选取输入步长为0.2 s,更符合一般车载电机的上升时间.由实验可知,在选取步长为 0.2 s的情况下,由于扰动变化过快,若采用文献[4]的控制方法无法正确地估计扰动,而本文提出的轨迹跟踪方法,其跟踪性能明显优于文献[4]提出的控制方法.
图2选取vx=3/m、φd=2π/20/rad作为参考轨迹Ⅱ.显然,在更符合实际场景0.2 s步长的情况下,本文提出的轨迹跟踪方法,其性能更好.
图3显示了控制信号变化率的性能差异.由图3可知,本研究所采取的方法,其控制信号的输入峰值更低;与文献[4]相比,本研究的控制器在运动过程中显得更加平稳,其控制方法不仅对外界环境的变化具有很强的鲁棒性,而且在固定时间内,对动态估计和补偿系统的总扰动,也具有较快的估计误差收敛性和良好的干扰估计性能.
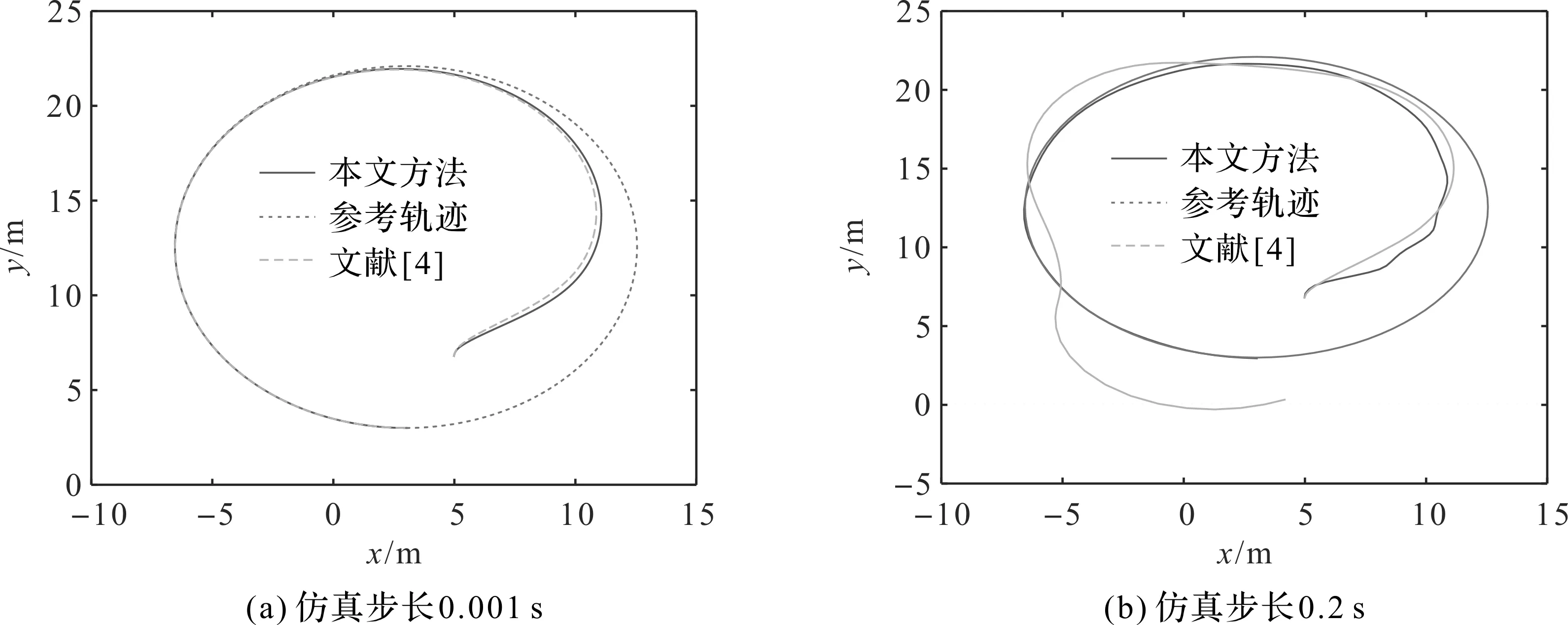
图2 参考轨迹Ⅱ跟踪的比较Fig.2 Reference trajectory tracking comparison Ⅱ
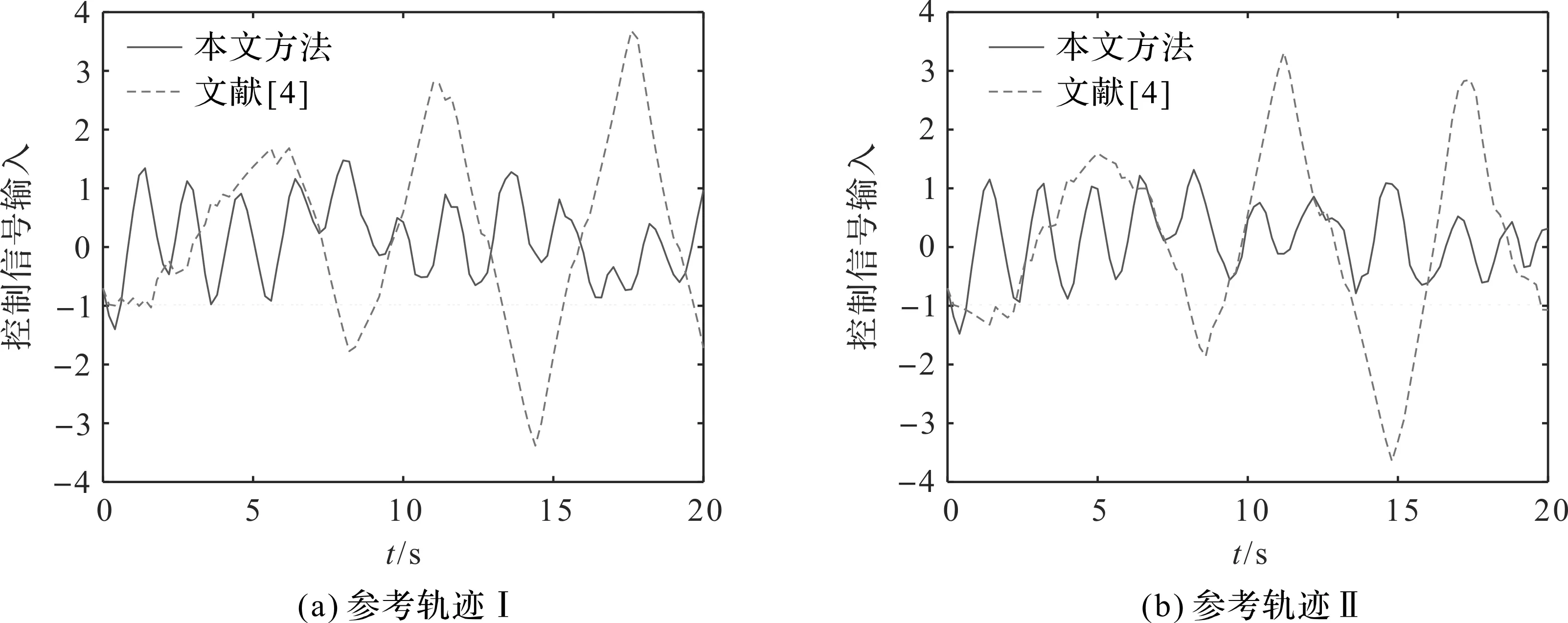
图3 控制信号输入比较(步长0.2 s)Fig.3 Comparisons of control signal inputs (step size is 0.2 s)
5 结 论
本文针对AGV系统轨迹跟踪问题,提出一种采用数据驱动型复合扰动观测器的控制方法,通过改进LOS制导策略、设计时变制导参数来处理误差系统的非线性项;针对动力学模型完全未知的情况,通过引入时变延时估计来提供预先补偿,再结合固定时间观测器,组成数据驱动型复合扰动观测器,以实现精准的扰动估计.基于上述工作,提出新的轨迹跟踪控制律,以实现高效精准的轨迹跟踪控制.由于受车辆本身的机械限制,执行器通常存在死区特性,当控制信号处于死区区间时,执行器无输出信号,从而增加了对未知动态与扰动的估计难度,使得系统稳态误差和性能下降.因此,受执行器死区影响的AGV轨迹跟踪仍然是一个有待解决的问题.而将一些非线性系统的样本数据控制方法[13-14]应用于AGV是一个值得探究的问题.此外,AGV技术已广泛用于物流分拣[15],但在分拣过程中若能考虑能耗优化控制,则是另一个值得研究的课题.
