亥姆霍兹共振式声电换能系统研究

2022-05-30马智宇吕海峰叶俊杰张文辉

振动与冲击 2022年10期

马智宇，吕海峰，叶俊杰，张文辉

(中北大学机械工程学院，太原 030051)

噪声污染是环境中常见的一种污染，长期处于噪声污染环境中，给人的生活质量以及身体健康带来恶劣影响。同时，噪声能量作为一种可再生能源，蕴含着巨大的能量。如何利用噪声能源，成为世界各国研究的热点问题。随着微机电系统的快速发展，如何实现微机电器件的能源供给成为研究的关键问题，为此魏娴等[1]提出利用声能回收技术实现对微机电系统的能量自供给，表现出巨大的应用前景。

Faturrochman等[2]构建了一个双面光伏噪声屏障的原型，提出了能量转化技术与噪声消除结构结合的原理。Gu等[3]完整构建了光伏发电噪声屏障将噪声转化为电压，实现噪声发电约570 W。

中科院的罗二仓等[4]研发了行波热发电机，以热声振荡理论为基础，实现声波发电。Liu等[5]研发了基于机电(electromechanical Helmholtz resonator，EMHR)的声能发电机，该声能发电机由EMHR收集声能，由压电材料实现声能转化，简化了声能发电方法，在160 dB的声压环境下，收集到30 mW的输出功率。为提高声能发电机的输出电量，Yuan等[6]提出一种声能发电机的特殊结构设计，通过控制结构的质量改变共振频率，利用机电转化效应在共振频率下上升的特性，提高声能的收集效率。Noh等[7]提出了一种基于悬臂梁的声能发电机，实现机械谐振来最大化压电悬臂梁的能量输出，但发电机依靠单一悬臂梁发电，能量转化效率低。美国南卫理公会大学的Li等[8]提出了一种直管谐振器收集低频声波能量，采用单结构多悬臂梁发电，提高了能量转化效率，但获得谐振发电量需要110 dB的声压。西北工业大学的Zhou等[9]提出了一种双稳态声能收集器，通过谐振来收集噪声能量，可在相对较低的声压下也能达到谐振。

以上研究提出的一些声能采集的方法中，所使用压电材料进行声能转化时发电量低，难以利用；采用悬臂梁谐振收集声能吸声结构体积较大，发电功率密度低；声能转化的条件仍较为苛刻。

为解决以上声能发电机存在的问题，本文提出了一种亥姆霍兹共振效应与压电效应相结合的声电换能方法，从低频噪声回收声能。

1 声电换能系统工作原理

所提出的亥姆霍兹共振式的压电陶瓷声电换能系统由吸声结构、能量转化、能量存储三部分构成。其声电换能系统框架图如图1所示。环境噪声通过声电换能屏障聚集进入平波管的多亥姆霍兹共振器串联阵列中，串联的多亥姆霍兹共振腔增大了与环境噪声的接触面积，提升了腔内声能吸收量。这一部分为吸声结构的功能是：采集的噪声引发系统共振，一方面使环境噪声降低，另一方面导致固定于腔体表面的压电陶瓷片变形发电，形成声电能量转化；转化的电能通过电路储存在超级电容中，这一部分作为能量存储。收集到的电能可为无线传感器节点、低压电器等低功耗元件提供能量[10]。

图1 声电换能系统框架图Fig.1 Acousto-electric transducer system frame diagram

2 声电换能系统设计

2.1 吸声结构设计

亥姆霍兹共振器是声学领域经典的吸声结构。其声学振荡规律与弹簧-振子系统相同[11]，集总参数模型如图2所示。图2中：R为亥姆霍兹腔体半径；L为腔体高度；t为颈部高度；r为颈部截面半径；k为弹性质量系统的弹性系数；c为阻尼系数；m为质量。

根据弹簧-振子力学模型，亥姆霍兹共振腔的共振频率f0为

(1)

式中：c0为介质声速；V为空腔体积；Δt声学末端修正系数，其表达式为[12]

(2)

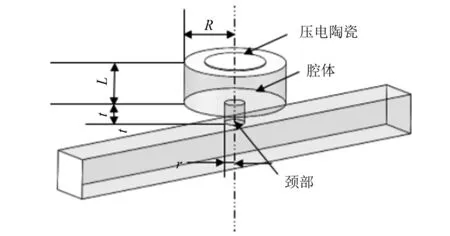
图2 亥姆霍兹共振器结构Fig.2 Helmholtz resonator structure

传递损失是结构输入端的声功率级与输出端声功率级之差[13]，它表征了结构自身的消声性能与共振频率的关系，是一种能准确地评价结构声学性能的声学参量。因此，采用传递损失作为评价声电换能结构声学性能及确定共振频率的方法。

计算常用声压为有效声压，用pe表示

(3)

式中，pA为声压幅值。

设置声电换能结构左端面为传声入口，右端面为传声出口。

矩形声波导管的简正频率为[14]

(4)

式中：lx为宽度；ly为高度；co为空气声速。对于一组不同的(nx,ny)数值将得到不同的简正模式的波。设计的声电换能结构宽度与高度相同，因此取(0,1)次波为声电换能结构的截止频率

(5)

将ny=1，ly=0.05 m，co=343 m/s代入，计算得fc=3 430 Hz。当声源频率低于截止频率3 430 Hz时，所设计的声电换能结构仅能传播平面波的管，简称平波管。

在平波管中，进出口声波均为平面波，传递损失(transfer loss ,TL)为

(6)

式中：Win为入射声功率；Wout为出射声功率。声功率W为

(7)

式中：S为截面积；ρ0为介质密度。

噪声通过颈部进入亥姆霍兹腔体后引起空气振动，当入射噪声频率与亥姆霍兹共振频率相同时，产生亥姆霍兹共振效应，腔体内声压放大，形成声波聚集。

集总参数模型如图2所示。换能单元由颈部，共振腔体与压电片组成[15]。颈部联通长方体平波管，与共振腔体形成亥姆霍兹共振器吸收外界噪声。进入颈部的空气振动使得压电片受力形变，从而产生电能[16]。

吸声结构设计用于接收来自外界的环境噪声，经平波管进入亥姆霍兹共振腔内形成声波聚集。将吸声结构单元在长方体平波管四周串联阵列分布，多个腔体及颈部有效吸收来自平波管的噪声[17]，扩大噪声吸收范围。吸声结构设计为宽为50 mm，高为50 mm，长为300 mm，厚度4 mm，截止频率为3 430 Hz的矩形平波管，材料为有机玻璃。在平波管表面分布半径为15 mm的换能单元，换能单元之间间隔40 mm。换能单元腔体厚度为1 mm，颈部半径0.5 mm厚度2 mm。

2.2 能量转化结构设计

亥姆霍兹共振器能够在声波的激励下发生共振，从而将声能耗散，达到噪声控制的目的。将压电片作为共振腔的基底，系统共振时压电片剧烈振动，由于压电效应会产生交变电荷，将电能收集起来加以利用便可以在噪声控制的同时，将声能转化为电能，实现能量的转换。压电陶瓷是声电换能的关键部件。研究过程选用压电陶瓷片PZT-5H，材料压电系数d33=640，d32=-283，机电耦合系数为3 400，相对介电常数为0.39[18]。

单片压电陶瓷片所产生的电量微弱，不足以驱动负载[19]。为使声电换能系统获得足够的电压，以满足用电器及电容充电条件，采用压电陶瓷片串联的方式提高系统的输出电压。

2.3 能量收集电路设计

声电换能结构产生的电能是交流电，无法直接为直流用电器使用或者进行储存。为了实现声电换能系统输出连续稳定的直流电，便于负载使用，设计了一种整流储能电路，其电路图如图3所示。声电换能器产生的交流电能由J1输入后，经整流桥D1GBJ2510进行交直流转化，直流电能储存于超级电容C1中。超级电容储存电量至一定值，可点亮LED灯D4，此时J2输出可为小型用电器供电。

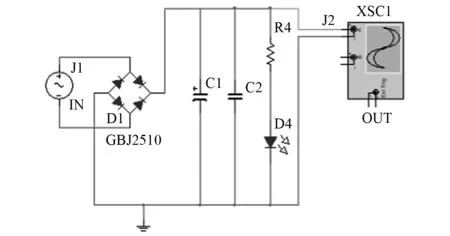
图3 整流储能电路图Fig.3 Rectifier energy storage circuit diagra

超级电容作为一种新型的储能元件，其电能储存量介于普通电容与电池之间[20]。超级电容与普通电容比较，电能储存量高于普通电容，且充放电时间更快，循环寿命更长；超级电容与电池比较，超级电容充放电迅速，可以大功率放电，不需要外接充放电控制电路，且使用寿命更长[21]。综合以上考虑，选用超级电容作为电能储能元件，对转化能量进行储存。

采用电路仿真软件multisim14.0对本文所提出的整流电路进行分析，验证采集电路采集交流电能的可能性，并进行交直流转化。使用2.6 V，380 Hz的交流电源等效J1输入，由示波器等效J2输出，接口A与输出端相连，接口B与输入端相连。

整流采集电路的仿真结果如图4所示，正弦波形为输入交流电压波形，趋于直线波形为输出直流电压波形。输入端电压始终交流变化，输出端电压由0增长至1.438 V后趋于稳定，以1.438 V的直流电压输出。仿真结果表明所设计的能量采集电路能够采集输入端的交流电能，并进行交直流转化。

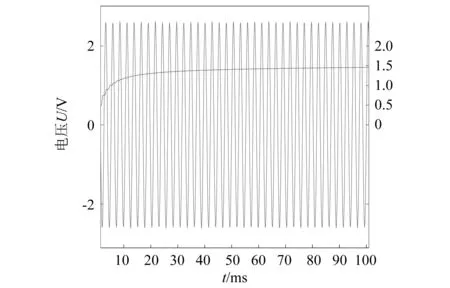
图4 仿真结果图Fig.4 Simulation results

2.4 声电换能结构的有限元仿真

采用有限元仿真软件COMSOL Muitiphysics 5.3a对所设计声电换能结构的机械性能进行仿真分析。

图5为声电换能结构的网格划分示意图，导入声电换能结构的几何参数。在压电片周围使用边缘固定约束，密度为1 300 kg/m3，弹性模量为2.6 GPa泊松比为0.47。设置压电片为固体力学物理场，并设置压电片中的压电材料为静电物理学场，压电片的上表面设置为电势平面，与铜片相接的下表面为接地，压电材料电荷守恒，初始电压为0[22]。设置空气腔体部分为声学物理场，分别设置声波进口和出口，利用声固物理场耦合，压电效应求解模型的传递损失及产生的电能。

图5 声电换能结构网格划分图Fig.5 Grid division diagram of acoustic and electrical energy exchange structure

声电换能结构仿真计算的声压云图如图6所示，入射声波为仿真共振频率400 Hz时，左端入射声波被聚集至各个亥姆霍兹腔体中，至右端出口时，声波出现明显损耗，声压级明显降低。

图6 声电换能结构400 Hz声压云图Fig.6 Acoustic and electrical energy exchange structure 400 Hz sound pressure cloud diagram

将声电换能结构在不同频率下的传递损失计算结果与压电效应产生的电能计算结果绘制于图7，虚线为声电换能结构的传递损失，左侧Y轴数据表示传递损失，实线为声电换能结构的总电能，右侧Y轴数据表示总电能。

声电换能结构的TL曲线在400 Hz处达到峰值，声波入口与声波出口的传递损失为10.47 dB。系统总电能亦在400 Hz处达到最大值，说明该频率为系统的共振频率，是由亥姆霍兹共振腔的存在而出现的，因而具有明显的窄带特性。因此声电换能结构在亥姆霍兹共振频带处的转换效率最高，同时产生的传递损失最大，在对噪声控制的同时，实现了声能到电能的转换。

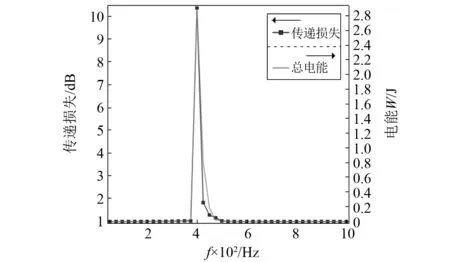
图7 传递损失-总电能曲线图Fig.7 Transfer loss- total power curve

3 声电换能系统性能测试

3.1 声学性能测试

为了研究所设计系统的声学性能，采用双负载法对声电换能装置的声压进行测量。图8为声压测量装置，主要由扬声器、功率放大器、信号采集卡、计算机和传声器组成。由计算机控制功率放大器和扬声器输出平面波信号向声电换能系统传播，利用传声器测量出声电换能系统入口处和出口处的声压，计算出声电换能系统的噪声控制效果。

图8 声学性能测试图Fig.8 Acoustic performance test diagram

设测量的声压为p，pA为有效声压，由于输入声波为正弦波，因此有效声压的计算式为

(8)

式中，pm为声波峰值。有效声压可用于声强计算，声强的计算式为

(9)

式中：ρ为空气密度；c为空气中的声速。声强可用于计算声功率，声功率的计算式为

W=I×S

(10)

将入口声压峰值pm0为5.008 Pa代入式(8)、再将算得入口声压pA0代入式(9)、计算得到的入口声强I0代入式(10)，得到声功率

W0=7.14×10-3W

(11)

同样：将出口声压峰值pm1为3.02 Pa代入式(8)～式(10)分别计算得入口声强pA1、出口声强I1和声功率

W1=2.51×10-3W

(12)

声电换能系统入口声功率与出口声功率元件的差值即为声电换能系统的噪声控制声功率We

We=W0-W1=4.63×10-3W

(13)

将入口的声功率与噪声控制声功率代入，计算噪声控制效率ε

(14)

由上述计算得到声电换能系统的噪声控制效率ε为64.8%，验证了该声电换能系统的吸声效果良好。

3.2 电学性能测试

为了验证所设计系统的电学性能，建立了图9中的试验装置测试系统的负载驱动能力。

试验过程中使用功率放大器及扬声器模拟外界噪声，通过传声器测量得到的噪声声压级为90 dB。通过PC机正弦脉冲软件调节噪声频率。将两个相互串联的声电换能系统安装于试验段，吸收来自扬声器的声波，采用10 k定值电阻作为负载。采集卡与10 k电阻两端相连，采集声电换能系统产生的电压信号,通过调节入射噪声频率从25 Hz上升至900 Hz，步长为5 Hz，采集不同噪声频率下声电换能结构产生的电压，测试结果如图10所示。

图9 声电换能装置图Fig.9 Diagram of acoustoelectric energy exchanger

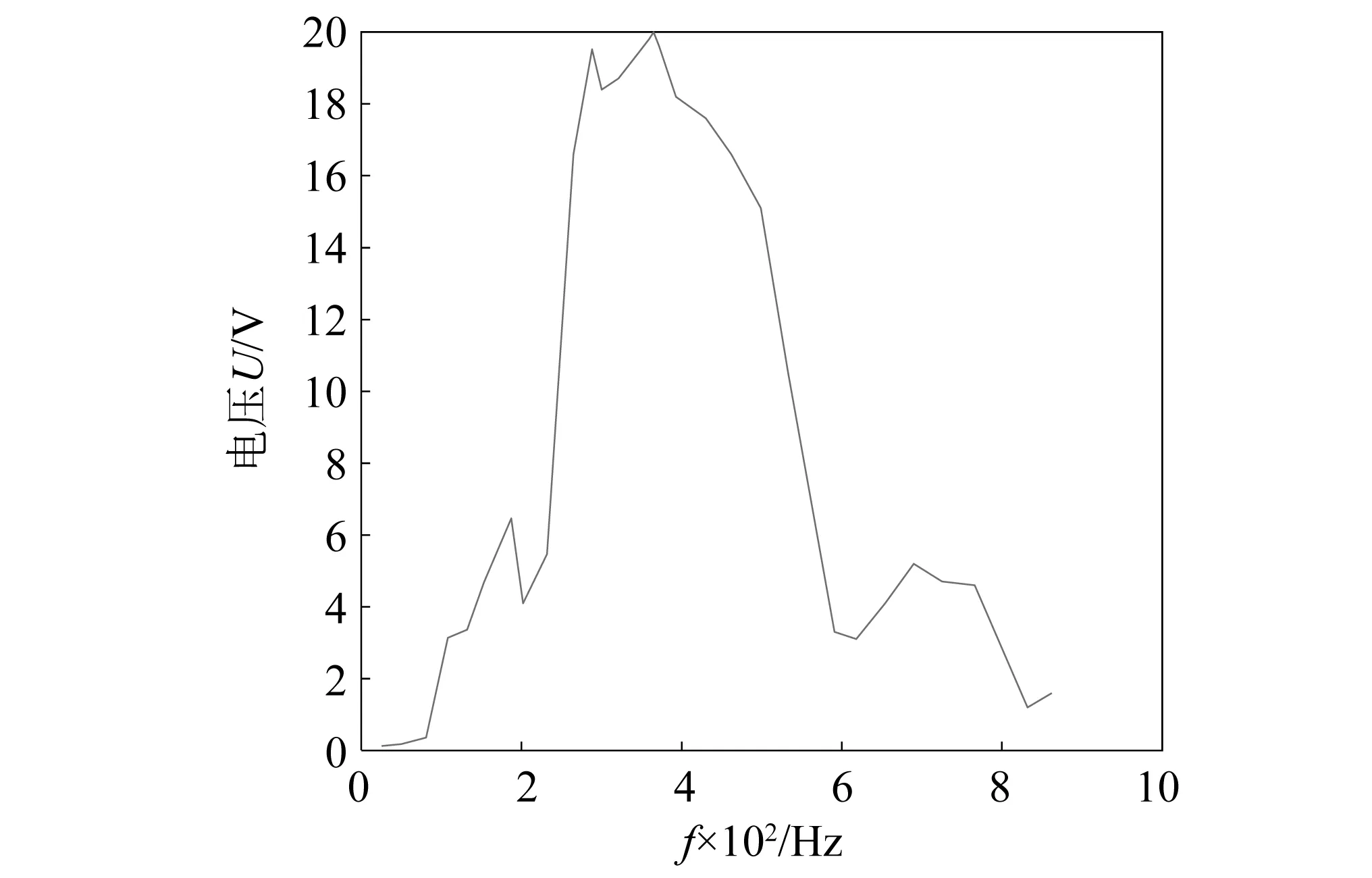
图10 不同频率下的电压Fig.10 Voltage generated by noise at different frequencies

结果表明，当噪声在结构的最佳谐振频率365 Hz附近，声电换能系统达到峰值电压20 V。当噪声的频率处于低频段0～100 Hz，噪声频率远离共振频率，声电换能系统产生电压极小，低于2 V。当噪声大于100 Hz时，噪声频率逐渐趋于共振频率，因此产生的电压升高。当噪声大于225 Hz时，声电换能系统所产生的电压立即突增，增至18 V左右，当噪声达到365 Hz时，声电换能系统所产生电压也达到了20 V。当噪声频率大于530 Hz时，噪声频率远离共振频率，共振效应基本消失，噪声共振产生电压也随之下降。

声电换能系统在最佳谐振频率下，输出电压20 V，测得输出电流为0.15 mA，此时声电换能系统的发电功率用Wm表示

Wm=ue×ie

(15)

式中：ue为声电换能装置的输出电压有效值；ie为输出电流有效值。

平均功率密度用E表示

(16)

式中：Wm为发电功率；V为声电换能结构的体积。声电换能结构体积为

V=lx×ly×h-(lx-2t)×(ly-2t)×h

(17)

式中：lx为宽度；ly为高度；h为长；t为厚度。将声电换能系统几何参数、试验测得输出电压及输出电流代入式(15)～式(17)分别计算得发电功率为3 mW，声电换能结构体积为220.8 cm3，平均功率密度为13.58 μW/cm3。

该系统入口接收到的声功率为W0，发电功率为Wm，噪声转化效率η

(18)

式中：入口接收的声功率W0为7.14 mW；发电功率Wm为3 mW。计算得，声电换能装置的噪声转化效率η为42.01%。

将获得的试验结果与已有的声能采集研究进行比较，由于各研究采用的激励条件不同，各研究采用的声压级不同，因此将噪声转化效率作为评价标准，对比结果如表1所示。表1表明：相对现有的研究结果，本文设计的声电换能装置在较低的噪声级激励下，仍保持较高能量转化效率。

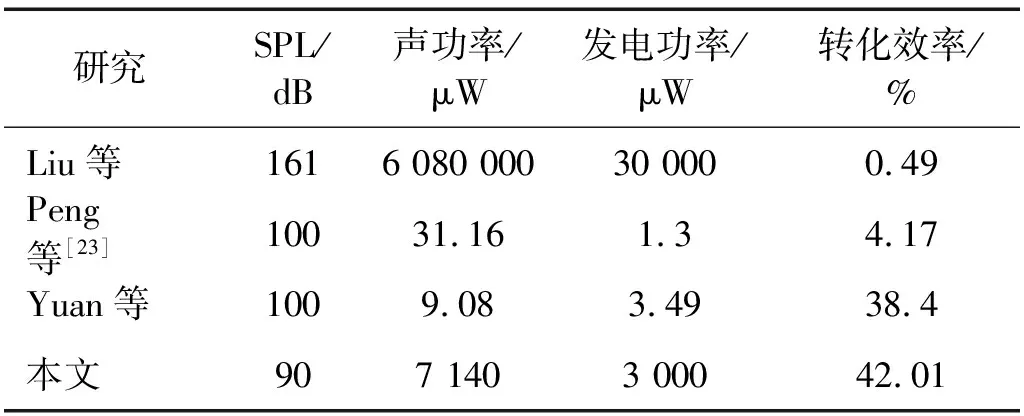
表1 声能采集研究发电性能比较Tab.1 Comparison of power generation performance in acoustic energy collection research

3.3 驱动能力测试

不同声波频率下二极管组板发光情况的对比结果，如图11所示。当噪声频率低于200 Hz时，发光二极管组板几乎不发光。当噪声频率大于500 Hz时，发光二极管组板发光微弱。

图11 不同频率二极管组板发光情况对比Fig.11 Comparison of light emitting from diode panels at different frequencies

比较不同频率声波激励时的发光二极管发光效果可知，在0～230 Hz低频段，声电换能结构供电量小，不适合给用电器供电。在230～500 Hz共振频带附近，适合给用电器供电。当噪声频率大于500 Hz时，声电换能结构供电量较小且供电量不稳定，不适合给用电器供电。在365 Hz共振频率下，二级管组板发光效果最好，此时声电换能结构的发电功率最大。因此，当系统工作于共振频率时，所产生的电能相对较大，可以为低压用电器提供能量供给，实现低频段噪声控制。