转动地震动对隔震结构动力响应的影响分析

韩 淼， 王延森， 杜红凯， 孙 猛， 刘永波

(北京建筑大学 北京未来城市设计高精尖创新中心，北京 100044)

Rosenblueth[1]于1957年首次提出了地震动不仅存在平动分量，同时也存在转动分量。观测到的地震震害现象亦表明地震动存在转动分量，尤其是在震源附近区域表现的更加显著。目前，关于地震动平动分量的研究已形成比较完善的理论，并广泛应用到工程实践中，但转动分量对结构地震响应产生的影响并未被充分认识，主要原因是受限于现有的转动加速度测量仪器还不足以在工程中实际应用，缺少通过设备直接测量的转动加速度数据。相关研究[2]所使用的地震动转动分量数据，基本上均是通过理论分析等方法间接得到，获取方法主要有基于弹性波动理论的行波法、频域法，以及两点差法等。

Newmark[3]最早利用行波法得到地震动扭转分量，并用于一个单层对称结构的地震响应分析，发现扭转分量作用会使角柱和端部剪力墙的应力增大，且对扭转刚度越大的结构影响也越大。Hart等[4]通过对平动加速度时程进行微分获得转动加速度，分析在加利福尼亚南部的几座高层建筑中获得的环境和地震响应记录，发现扭转分量对结构的扭转地震响应有较大影响。Nathan等[5]用地基两侧相对位移的差值与相对距离的比值作为自由场地扭转分量的平均估计值，对RC框架结构仅在水平地震作用下和考虑扭转地震动时的地震响应进行分析，得出考虑地震动扭转分量后会使对称和非对称结构的角柱弯矩分别增大14%和35%。Ghafory-Ashtiany等[6]采用行波法的假定，考察地震动六分量沿结构主轴作用对结构内力响应的影响，结果显示随着结构尺寸增大，扭转分量对结构响应贡献会增大。

陈向上等[7]建立框架结构有限元分析模型，输入平动与转动地震加速度研究表明，输入双向平动地震动及扭转地震动相比于仅输入单向平动地震动会增大框架结构各层的位移反应13%以上。楼梦麟等[8]建立超高层结构的三维有限元模型，分别计算在地震动平动分量和转动分量作用下结构地震响应，得出考虑转动分量时结构顶层加速度增加35%，楼层层间位移均有所增大。陆铁坚等[9]对剪切型高层建筑在地震动水平和摇摆分量共同作用下的随机反应进行研究，表明地震动摇摆分量对上部结构的位移响应影响较大。李宏男等[10]对地震动水平与摇摆分量共同作用下的输电塔-电缆体系的地震响应进行分析，发现不论是在横向还是在纵向，摇摆分量对塔横档以下附近的剪力影响最大，摇摆分量对输电塔这类高耸结构有较大影响，不应忽视。陈国兴等[11]建立六维地震动运动方程，探讨地震动转动分量对于对称框架结构的影响，得出地震动扭转分量对角部构件的地震响应影响随着长宽比的增大而增大，摇摆分量对高频结构地震响应的影响比低频结构大。王君杰等[12]研究地震动扭转分量对薄壁圆柱壳结构的影响，表明转动分量对安全壳和储油罐等结构的基底剪应力的贡献可达到平动分量的30%以上。张杰等[13]对大跨非对称空间结构在多维地震动作用下的结构响应进行研究，显示地震动扭转分量对于结构基底外围及拐角处的支柱内力峰值有较大影响。魏文晖等[14]对地震动水平、竖向和摇摆分量共同作用下高柔结构的动力响应进行理论推导和缩尺模型振动台试验研究，表明摇摆分量导致结构水平位移幅值大幅增加。王昌盛等[15]对考虑扭转分量的双向偏心隔震结构的减震效果进行分析，表明隔震装置对偏心结构的平动位移和扭转响应的控制效果显著，而且在地震动扭转分量作用下的结构扭转响应会减小。

地震动转动分量对抗震结构动力响应影响的研究已取得一定成果，但对隔震结构动力响应影响的研究较少。本文将建立对称钢筋混凝土框架结构的抗震和隔震结构模型，计算三向平动分量、三向转动分量和平动与转动耦合六分量地震动作用下的结构响应，分析地震动转动分量作用对结构动力响应的影响。

1 地震动转动分量

1.1 转动分量获取的频域法

实际地震动是由地震波的振幅、频率和相位等共同决定的复杂运动，对于某一特定的地震动时程记录，可由数条简谐波的叠加来表示。基于弹性半空间理论，假定地震波的传播介质是均匀弹性的，采用频域法可由实际记录到的地震动平动分量来获得转动分量，计算公式为

(1)

(2)

(3)

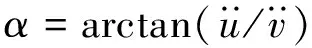
(4)

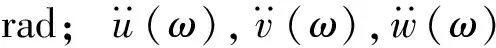
由式(1)～式(3)得到转动分量的傅里叶谱后，再对其进行傅里叶逆变换，即可得到转动分量的加速度时程。

1.2 平动地震波的选取

从PEER地震波数据库选取震中距20 km以内的近断层地震波，共选取4条1999年中国台湾集集地震的地震记录，其中含有速度脉冲2条，记为 Ⅰ 组，不含速度脉冲2条，记为 Ⅱ 组。地震波的相关信息见表1。地震记录的EW向、NS向和V向依次记为x向、y向和z向。

表1 地震波基本信息Tab.1 Basic information of seismic waves

1.3 地震动转动分量的合成

由频域法计算可得到4条地震波的三向转动分量角加速度时程，单位为rad/s2，绕x，y，z轴转动的三个转动分量依次记为Rx，Ry，Rz。

图1和图2绘出波1和波3的z向平动分量与合成的Rx向转动分量速度时程，可以看到，含有速度脉冲平动分量合成的转动分量也含有速度脉冲，无速度脉冲平动分量合成的转动分量没有明显的速度脉冲。

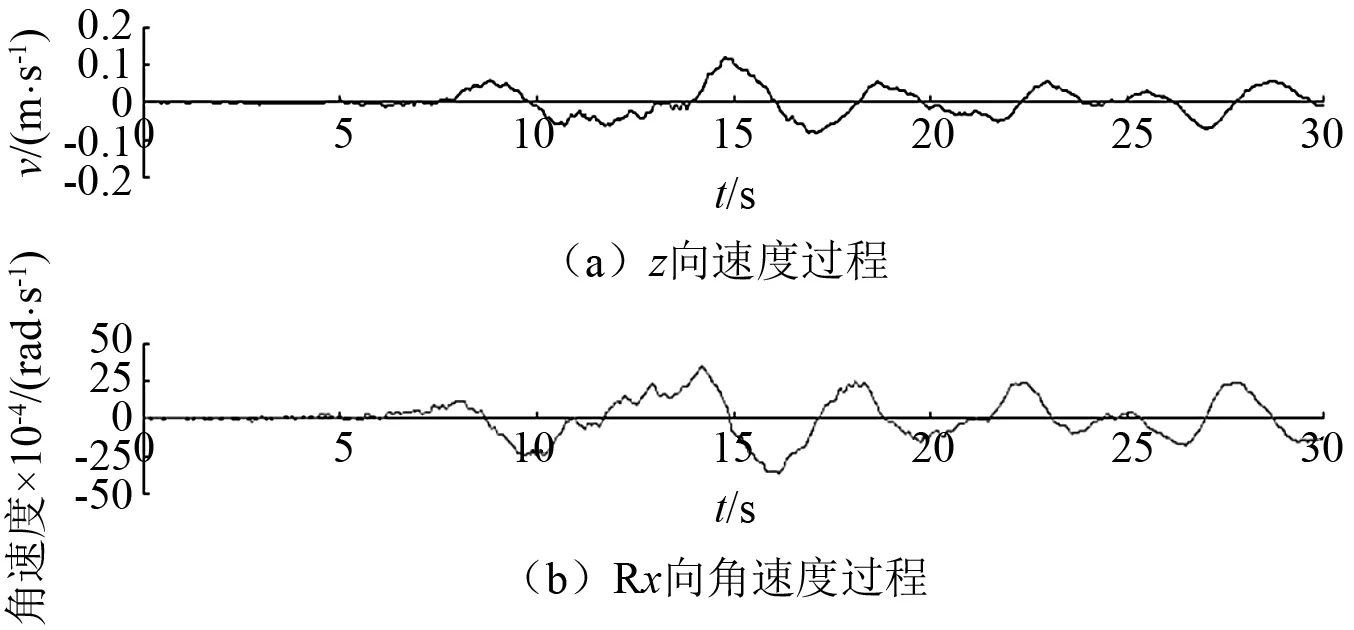
图1 波1的平动分量与转动分量速度时程对比Fig.1 Comparison of the velocity time history of the translational and rotational components of wave 1

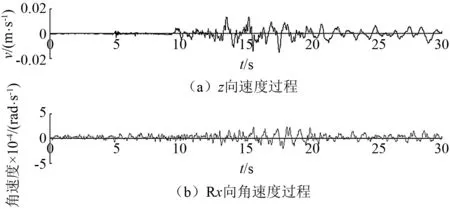
图2 波3的平动分量与转动分量速度时程对比Fig.2 Comparison of the velocity time history of the translational and rotational components of wave 3

2 结构分析模型

2.1 抗震结构模型

设计一个6层钢筋混凝土框架结构模型，设防类别为丙类，设防烈度为8度(0.2g)，场地类别为Ⅱ类，设计地震分组第二组。标准层平面如图3所示，长×宽为18 m×18 m，层高均为3.6 m，建筑总高为21.6 m；框架柱截面600 mm×600 mm，框架梁截面300 mm×700 mm，楼板厚120 mm；受力纵筋采用HRB400钢筋，混凝土采用C30。

利用ABAQUS软件建模，梁柱采用B31梁单元，楼板采用S4R壳单元，结构模型的三维空间视图，如图4所示。

图3 标准层平面图Fig.3 Plane figure of standard floor

图4 三维空间视图Fig.4 Three-dimensional view

表2给出由ABAQUS软件建模计算得到的结构前3阶振型自振周期T，与SAP2000软件计算周期T′对比，误差在3.4%以内。

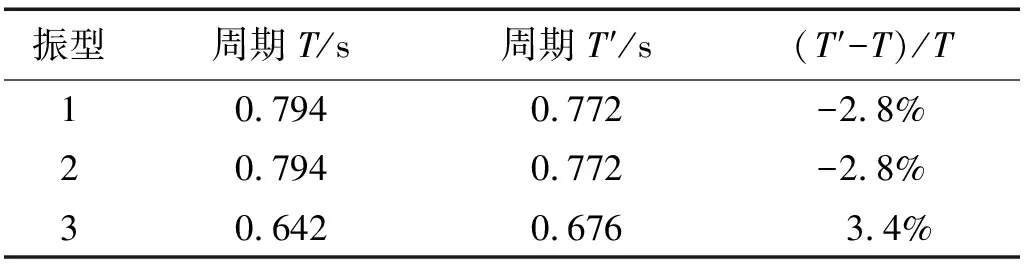
表2 抗震结构自振周期Tab.2 Natural vibration period of frame structure

2.2 隔震结构分析模型

在抗震结构模型的基础和上部结构之间设置隔震层，得到隔震结构分析模型。考虑隔震支座宜对称分散布置，将铅芯橡胶支座LRB500沿结构周边布置，以减少扭转效应，同时充分发挥铅芯的耗能能力；在结构平面的中部布置天然橡胶支座LNR500，隔震支座的平面布置如图5所示。隔震支座性能参数如表3所示。

图5 隔震支座LRB500和LNR500的布置Fig.5 The arrangement of isolated bearings LRB500 and LNR500

表3 隔震支座性能参数Tab.3 Performance parameters of isolated bearings

表4给出由ABAQUS软件建模计算得到的隔震结构前3阶振型自振周期T，与SAP2000软件计算周期T′对比，误差在8.3%以内。

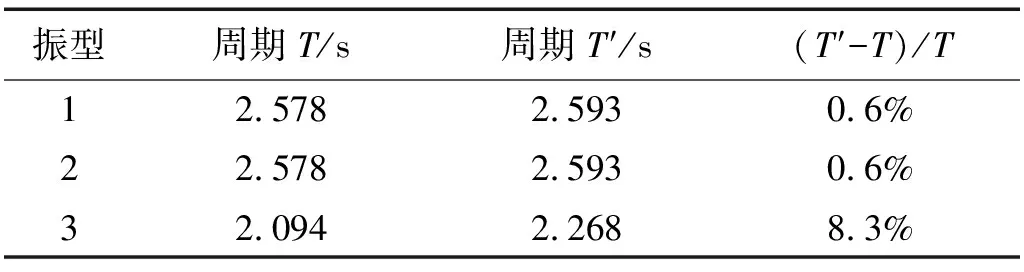
表4 隔震结构自振周期Tab.4 Natural vibration period of isolated structure

3 地震动输入工况

结构模型动力响应分析，考虑三种地震动分量的输入工况：

工况一仅输入地震动平动分量，x，y，z三个方向的平动分量同时输入，记为工况T；

工况二仅输入地震动转动分量，Rx，Ry，Rz三个方向的转动分量同时输入，记为工况R；

工况三同时输入平动分量和转动分量，x，y，z三向平动分量和Rx，Ry，Rz三向转动分量同时输入，记为工况TR；

4 结构模型动力响应分析

结构设防烈度为8度(0.2g)，将地震动平动分量的加速度峰值调幅为8度罕遇地震峰值400 cm/s2，转动分量也相应调幅。按照三种工况，将三向平动分量、三向转动分量和平动与转动耦合六分量地震动分别输入抗震和隔震结构模型，计算结构动力响应。考虑结构模型平面对称，选取角柱在各楼面处的加速度、柱端剪力，以及楼层位移响应(包含平动位移和楼层扭转角)，作为结构动力响应的评价指标。

4.1 水平方向加速度响应分析

图6绘出隔震结构各楼层x向、y向最大加速度响应沿楼层的分布曲线，从图6可知:

(1) 转动分量单独作用工况R在x向、y向的最大加速度大小不同，这是由转动分量中摇摆分量的大小不同决定的。结构顶层最大加速度响应，工况R与工况T的比值R/T在不同地震动作用下为0.28～2.00，最大值达到2.00，表明转动分量可能会对结构的最大加速度响应产生较大影响，某些情况下甚至达到平动分量作用下加速度响应的2倍。

(2) 工况TR与工况T的结构x和y向顶层加速度响应比值TR/T，含有速度脉冲的Ⅰ组地震动作用下为0.9～2.0，无速度脉冲的Ⅱ组为1.0～2.3，Ⅱ组比值较大的原因，是其工况T加速度响应相对较小。最不利情况下，转动分量与平动分量耦合作用下，隔震结构y向顶层加速度响应会增大100%以上。

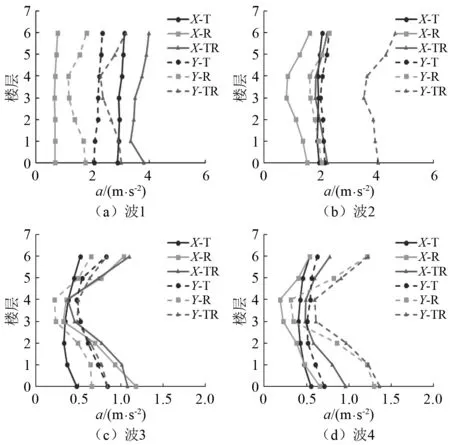
图6 不同地震动作用隔震结构楼层最大加速度比较Fig.6 Comparison of the maximum acceleration of each layer of the isolated structure under various seismic waves

表5给出了抗震结构与隔震结构的x向顶层最大加速度响应，其中减震比表示隔震与抗震结构的动力响应之比，比值越小，说明隔震结构的减震效果越好。从表5可知：

(1) 隔震对工况T的结构响应减震效果最好，减震比为4%～27%；对于工况TR的减震效果次之，减震比为6%～29%；对于工况R的减震效果最差，减震比为29%～81%。橡胶支座隔震对转动分量产生的顶层加速度的减震效果，相比平动分量较差。

(2) Ⅰ组、Ⅱ组地震动作用下工况TR减震比分别在25%、10%左右，隔震对含有速度脉冲的Ⅰ组地震动作用的减震效果比无速度脉冲的Ⅱ组地震动的差。

表5 抗震结构与隔震结构x向顶层最大加速度响应对比Tab.5 Comparison of the x-direction maximum acceleration response of frame structure and isolated structure

4.2 水平方向层间位移响应分析

图7绘出隔震结构各楼层x向、y向最大层间位移响应沿楼层的分布曲线，从图7可知：

(1) 楼层最大层间位移沿高度分布呈现为反C形。有速度脉冲的Ⅰ组地震动作用下，含有平动分量的2个工况(T、TR)的最大层间位移均大于弹性层间位移限值3 600/550=6.5 mm，表明结构进入弹塑性状态，最大层间位移出现在第2层，在结构设计时应注意加强；工况R作用的结构处于弹性状态。无速度脉冲的Ⅱ组地震动作用下，结构处于弹性状态。

(2) 在工况T层间位移响应较大方向，工况R与相应工况T的比值R/T为0.20～0.52，其中，Ⅰ组地震动作用x方向的R/T为0.20～0.30，Ⅱ组地震动作用y方向的R/T为0.43～0.52，表明转动分量会对结构的最大层间位移响应产生影响。

(3) 在工况T层间位移响应较大方向，TR/T的比值，Ⅰ组地震动作用的x向为0.83～1.17，Ⅱ组地震动作用的y向为1.03～1.25。表明转动分量与平动分量耦合作用的最大层间位移响应，相比于仅平动分量作用，最不利时，y向增幅可达25%。

图7 不同地震动作用隔震结构各层最大层间位移比较Fig.7 Comparison of the maximum story drift of each layer of the isolated structure under various seismic waves

表6给出抗震结构与隔震结构沿x向的最大层间位移响应，从表6可知：

(1) 隔震对于含有平动分量的2个工况(T、TR)减震效果相当，减震比为6.1%～26.9%，对于工况R的减震比为24.2%～59.3%，表明隔震对转动分量作用下层间位移响应的减震效果比对平动分量差。

(2) Ⅰ组、Ⅱ组地震动作用下工况TR的减震比分别在26%、8%左右，隔震对含有速度脉冲的Ⅰ组地震动作用的减震效果比无速度脉冲的Ⅱ组地震动的差。

表6 抗震结构与隔震结构x向最大层间位移响应对比Tab.6 Comparison of the x-direction maximum story drift response of frame structure and isolated structure

4.3 层间扭转角响应分析

图8绘出隔震结构各楼层最大扭转角沿楼层分布曲线，从图8可看出：

(1) 工况T下扭转角底层最大，从1层～2层减小明显，2层以上楼层几乎相同，总体分布呈现L形。

(2) R、TR两个含有转动分量工况的楼层扭转角，沿楼层的分布曲线具有很高的重合度，总体呈现反C形，最大扭转角几乎均出现在第2层。TR/T的比值，Ⅰ组和Ⅱ组地震动作用分别为10.1～20.1和18.6～18.7，转动分量与平动分量耦合作用，相比于仅平动分量作用的增幅可达10倍以上，说明结构各楼层扭转角主要由转动分量贡献。转动分量作用会大幅增加结构的扭转效应，尤其对中下部楼层的影响更大，将会使角柱内力响应加剧，隔震设计时应考虑地震动转动分量的影响。

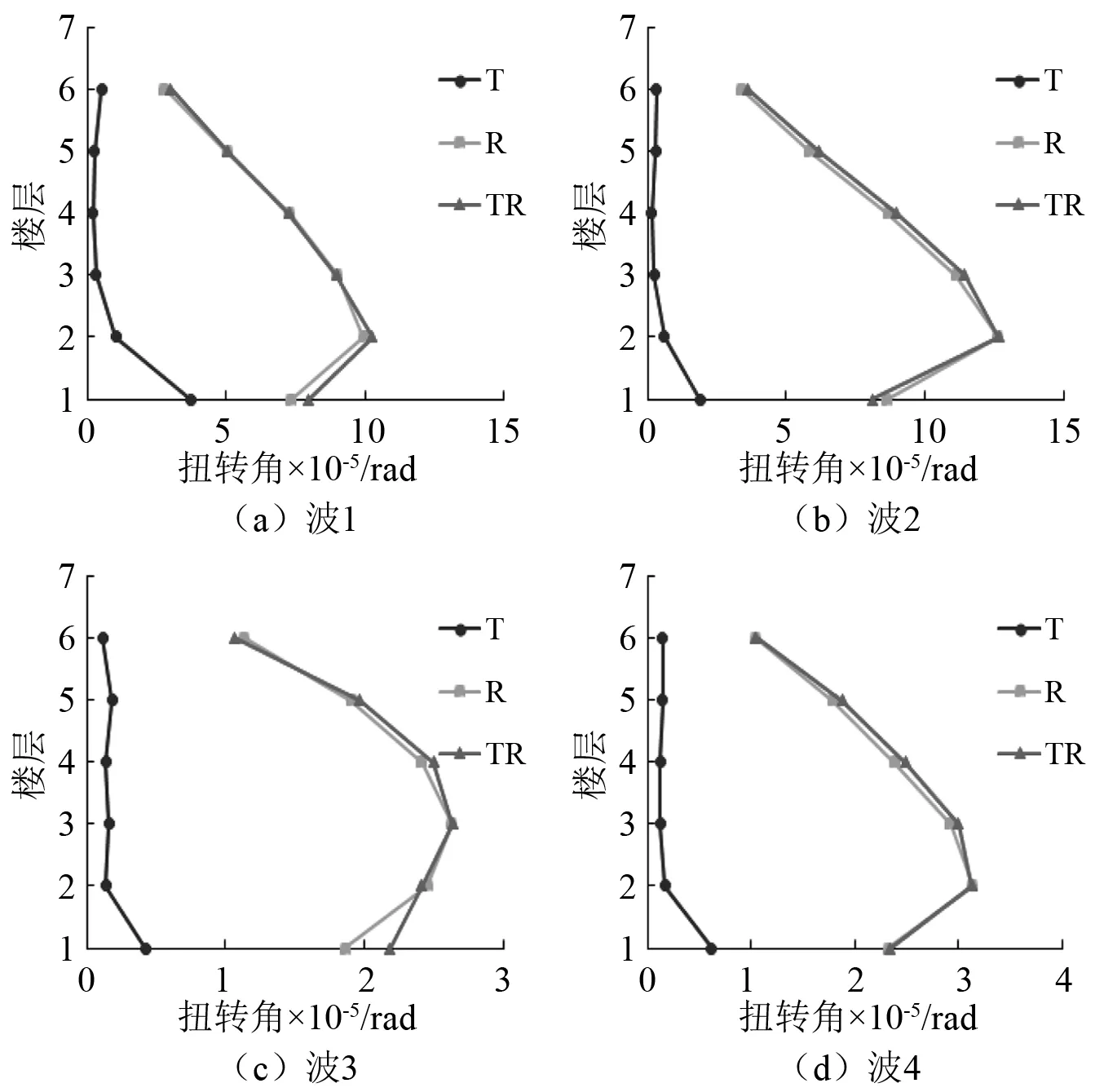
图8 不同地震动作用隔震结构各层最大扭转角比较Fig.8 Comparison of the maximum distortion angle of each layer of the isolated structure under various seismic waves

表7给出抗震结构与隔震结构的楼层最大扭转角响应，由表7可知：

(1) 隔震对工况T的楼层最大扭转角具有很好的减震效果，减震比为1%～2%，对于工况TR的隔震效果次之，减震比为5%～12%，对于工况R的减震效果稍差，减震比为11%～29%，表明隔震对于平动分量作用下的楼层扭转角具有很好的减震效果，对于转动分量作用也有较好的减震效果。

(2) Ⅰ组、Ⅱ组地震动作用下工况TR的减震比分别在10%、6%左右，隔震对含有速度脉冲的I组地震动作用的减震效果比无速度脉冲的II组地震动的差。

表7 结构与隔震结构最大扭转角响应对比(1/1 000 rad)Tab.7 Comparison of the maximum distortion angle response of frame structure and isolated structure

4.4 柱端剪力响应分析

图9绘出隔震结构的上部结构角柱最大柱端剪力沿楼层的分布曲线，从图9可知：

(1) 上部结构角柱最大柱端剪力沿楼层主要呈现出向右下倾斜的斜线或竖直线的形态。

(2) 工况T柱端剪力响应较大方向，Ⅰ组地震动作用的x向R/T比值为0.26～0.29，TR/T的比值为0.92～1.18；Ⅱ组地震动作用的y向R/T比值为0.42，TR/T比值为1.04～1.15，表明转动分量与平动分量耦合作用下，相比于平动分量单独作用的最大柱端剪力的增幅可达18%。

图9 不同地震动作用隔震结构各层最大柱端剪力比较Fig.9 Comparison of the maximum shear force of corner column of each layer of the isolated structure under various seismic waves

表8给出抗震结构与隔震结构沿x向的角柱最大柱端剪力响应，由表8可知：

(1) 隔震对于2个含有平动分量的工况(T、TR)减震效果相当，减震比为12%～80%，对于工况R的减震效果相对较差，减震比为29%～83%，表明隔震对于转动分量作用下角柱剪力的减震效果相对于平动分量较差。

(2) Ⅰ组地震动作用下工况TR的减震比分别为80%、55%左右，而Ⅱ组地震动此值只有12%、15%。表明隔震对含有速度脉冲的Ⅰ组地震动作用的减震效果比无速度脉冲的Ⅱ组地震动明显较差。

表8 抗震结构与隔震结构x向角柱最大剪力响应对比Tab.8 Comparison of the x-direction maximum shear force response of frame structure and isolated structure

5 结 论

建立抗震与隔震结构的有限元分析模型，计算三向平动分量、三向转动分量和平动与转动耦合六分量地震动作用的结构响应，选取楼层加速度、层间位移、楼层扭转角和柱端剪力进行分析，评价转动分量对结构动力响应的影响，以及隔震的减震效果。

(1) 转动分量会对隔震结构的动力响应产生重要影响。转动分量与平动分量耦合作用相比于仅平动分量作用的结构响应，楼层y向最大加速度增幅可达100%以上，层间最大水平位移增幅可达25%，x向最大柱端剪力增幅可达18%，而楼层扭转角增幅可达10倍以上，这是因为结构楼层扭转角主要由转动分量贡献，转动分量作用会大幅增加中下部结构的扭转效应。

(2) 含有速度脉冲的Ⅰ组地震动作用的隔震结构动力响应，相比无速度脉冲的Ⅱ组地震动，明显增大，表明地震动速度脉冲对隔震结构动力响应具有不利影响。

(3) 隔震对转动分量作用的结构响应的减震效果，比对平动分量作用的减震效果差。隔震对于有速度脉冲地震动的减震效果，比对无速度脉冲地震动的减震效果差。