基于Grünwald-Letnikov定义改进的短记忆原理方法
2022-05-30马瑞群员海玮韩景龙
马瑞群, 张 波, 员海玮, 韩景龙
(南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016)
分数阶导数的概念可以追溯到微分学开始的时候,1695年,Leibniz[1]和L′Hpital在往来书信中开始讨论分数阶导数。随后,通过Euler、Liouville、Riemann、Letnikov和Coputo等伟大数学家的共同努力,奠定了分数导数的数学基础。然而,直到最近,分数阶导数在科学和工程的各个分支中的重要应用才得以确立。分数阶微分方程在物理学[2-5]、化学[6-7]和工程学[8-10]中扮演着越来越重要的角色。从时间上而言,整数阶导数所表征的是物理过程某时刻的物理量的变化,而分数阶导数所表征的性质则与该现象的整个发展历史有关。整数阶空间导数描述的是一个物理过程在空间中某一确定位置的局部性质,而分数阶导数所描述的性质则与物理过程所涉及的整个空间有关。尽管分数阶导数有很多种定义,但最常用的定义是Grünwald-Letnikov、Riemann-Liouville和Caputo分数导数。
由于时间分数阶导数具有的时间记忆性,其在数值求解过程中为了得到更加精确的结果会有大量的数据参与计算。分数阶微分方程数值近似解的方法已经被广泛研究[11-17],但是通常在计算效率、复杂性和结果近似的精度之间总是存在权衡。文献[18]提出了一种没有记忆效应的高效仿真方法。文献[19]提出短记忆原理(short memory principle,SMP),是指截取最近的一个时间段,而对影响比较小且较远的时刻选择忽略。文献[20]利用短记忆原理验证了周期函数的分数阶导数依然是周期函数。文献[21]结合短记忆原理和Grünwald-Letnikov定义,研究了分数阶系统的模型参考自适应控制。Wei等[22]根据Grünwald-Letnikov定义下的经典短记忆原理,提出并研究了几种新颖的短时记忆原理。传统的短记忆原理可能会带来较大的误差,例如自由振动不能回到平衡位置。尤其当分数阶数α趋于0时,为了保证计算精度用短记忆原理截取的记忆时间可能极其巨大。文献[23-25]提到用嵌套网格方法解决长时记忆,其中:Ford等提出在时间段的两端用小步长,但是随着时间推进,初始时刻附近的系数将变得很小且每一步都需要重新计算;Diethelm等所提方法则同样需要每一步重新计算系数。
本文提出一种基于Grünwald-Letnikov定义改进的短记忆原理。这种改进是把对记忆时间的截断调整为对二项式系数的截断。为了保证计算的精度,初始采用小步长。如果计算过的数据点数超过二项式系数的项数,则增大步长使有限的二项式系数能覆盖更大的时间区域。这种改进的目的是用尽量少的数据量求得比较精确的结果。文章中用单自由度分数阶阻尼受迫振动算例验证了方法的准确性和可靠性。
1 分数阶导数的记忆性
Grünwald-Letnikov定义为
(1)
式中,h为计算步长。如果选择的计算步长足够小,则求极限操作可以忽略,变为
(2)
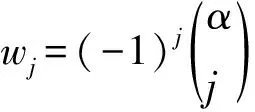
(3)
为了避免Gamma函数的计算,采用递推形式
(4)

wj是从当前时刻往前数j个步长间隔的时刻的函数值的加权系数,也即二项式系数。从递推公式的等号左边的系数小于1可知这个加权系数随着时间间隔的增大而减小。表1给出了当α=0.5时的部分二项式系数。可以看到加权系数的绝对值在开始阶段迅速减小,随后减小的速度越来越慢。从1~-0.01只计算了9项,后面依次减小10倍的项分别为w43,w200,w926,w4301,w19965,w92668和w430126。从-1.00×10-8~-1.00×10-9需要经历将近34万项,虽然每一个时刻对当前时刻影响很小,但是项数如此之多依然会带来很大的误差。
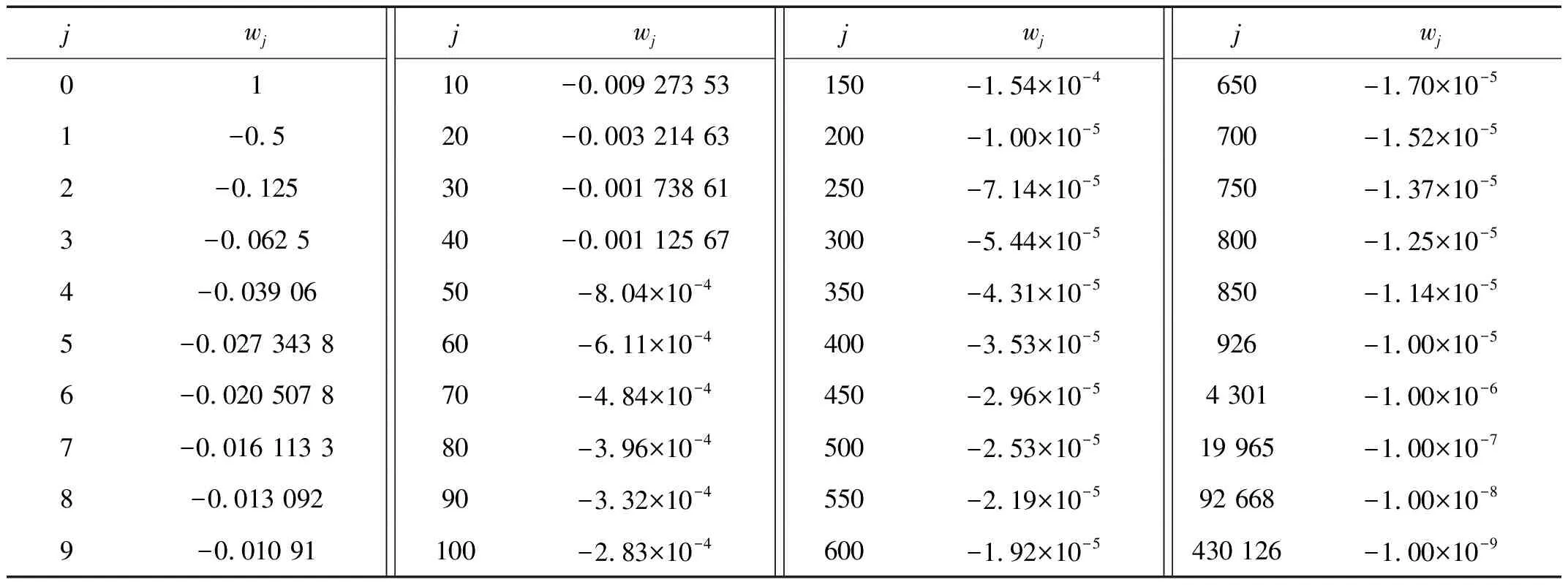
表1 当α=0.5时的部分二项式系数Tab.1 Partial binomial coefficient at α=0.5
2 改进的短记忆原理
Grünwald-Letnikov定义下分数阶导数计算时取值如图1所示。计算第k个时间步时,需要考虑前面所有时刻的影响。如果需要计算的时间步很多时,计算量将是非常庞大。此外为了获得较为精确的数值解,通常以减小时间步长为手段,这是计算量增大另一个因素。因此有了短记忆原理的提出,如图2所示。L为截取的记忆时间,反映在公式上是截断Nt项。如果步长为h,则L=Nt×h。短记忆原理公式为
(5)

图1 Grünwald-Letnikov原始定义示意图Fig.1 Grünwald-Letnikov original definition diagram

图2 短记忆原理示意图Fig.2 Schematic diagram of short memory
短记忆原理的提出的根据是,随着时间的推移,久远的时刻对当前时刻的影响越来越小,因此就进行有效截断处理。但是这种截断往往会带来不可忽视的误差。所以对短记忆原理进行改进。改进的思路是把短记忆原理对时间的截断替换为对二项式系数项数的截断。当计算时间超过L时,则把超出的部分时刻取值步长调整为初始步长的倍数。调整步长后,用小步长计算的时刻不用再次计算,只计算小步长范围外的部分,如图3、图4和图5所示。图中二项式截断项数为Nt=10,步长增大倍数为n=2。

图3 计算时间步数k≤NtFig.3 Calculation time steps k≤Nt

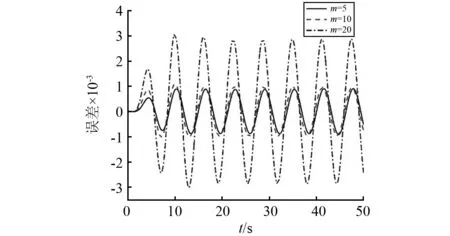
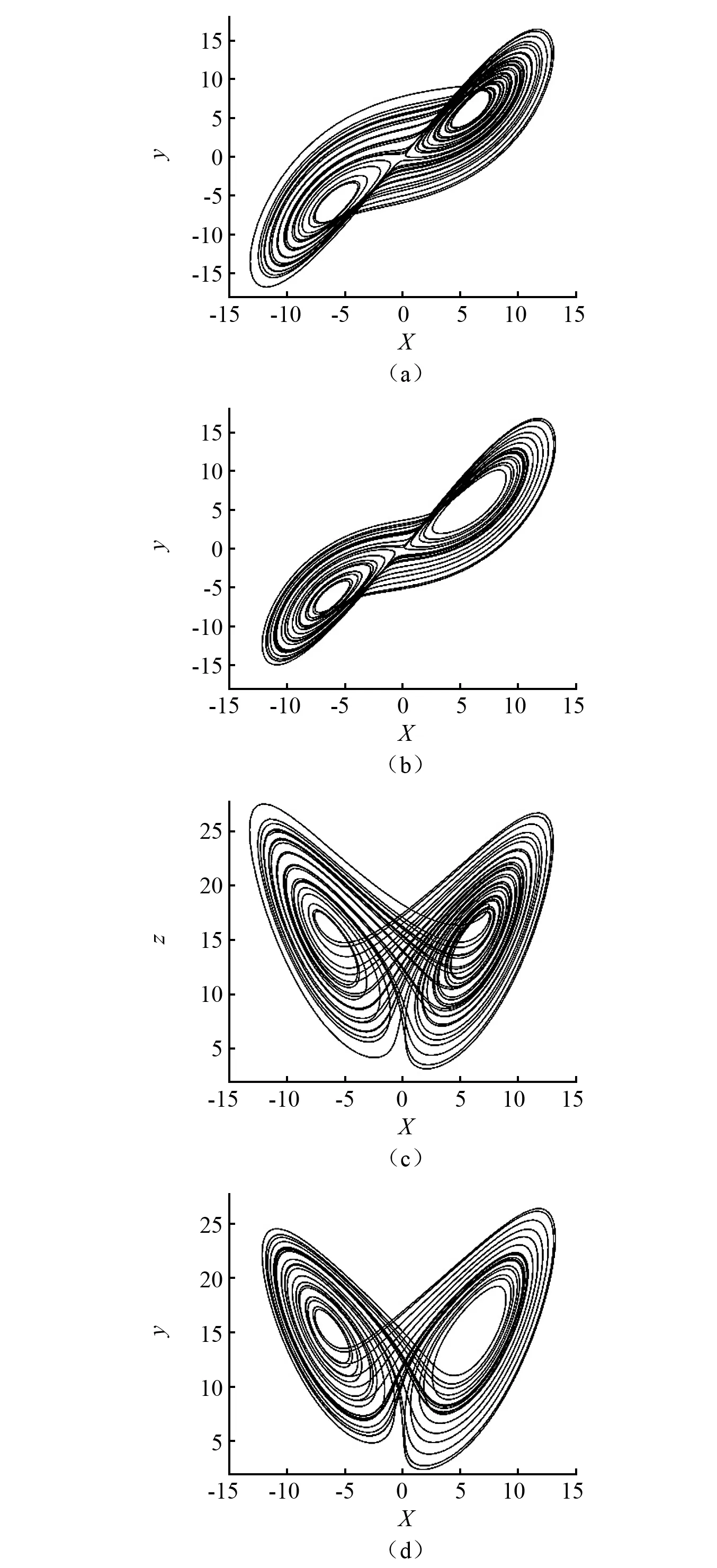
图4 计算时间步数Nt 图5 计算时间步数nNt 图3中计算步数k≤Nt,未到截断条件,则按照原始定义计算。表达式为 (6) 图4中计算步数Nt (7) 式中:a,b分别为[Nt/n]+1,[k/n];[·]为取整。步数nNt (8) 式中,d为[k/n2]。以此类推,可以得到更多的步长表达式。 理论上,初始截断项数Nt越大,所取得的结果越精确。但是考虑计算成本,会选择一个比较合适的值。至于步长放大倍数,换一个角度考虑。步长放大后,所取函数值可以看作为该间隔的代表。式(7)等号右边可以把公因子1/h1α提出来,则第二项包含二项式系数的第i项影响系数为(1/nα)wi,其与未放大步长时该函数值的影响系数比值几乎等于放大倍数n。以截断项数Nt=100,放大倍数分别为n=5,n=10,n=20为例,α=0.5部分比值如表2所示。 表2 当α=0.5时的部分影响系数Tab.2 Partial influence coefficient at α=0.5 可以看到第一次放大后,影响系数随着步数递增逐渐减小,越来越接近放大倍数n。随着放大倍数的增大,第一个影响系数变大,尤其当n=20时,大过该步长内初始步长的个数,因此会带来较大误差。另外所取时刻的函数值在该间隔内是否具有代表性,即所取函数值是否更接近该间隔内函数值的平均值。因为扩大步长取函数值是一个动态的遍历过程,所以在长时计算中引起的误差也有限。综上所述,在计算条件允许下尽量截取更多的二项式系数,以及选取较小的步长放大倍数,才能获得更为精确的数值解。 采用带有分数阶阻尼的振动微分方程为例,方程形式为 (9) 接下来考虑不同截断项数的情况。设置所有的基础步长h=0.000 1,所有步长放大倍数为n=10。断项数分别为Nt=3 000,Nt=10 000,Nt=30 000,所对应的初始记忆时间为0.3 s、1 s和3 s。具体数值结果与图6无异,由于误差量级较小,看不到区别。其误差结果如图8所示。黑色实线为Nt=3 000时与原始定义数值解之间的误差,与另外两条线相比幅值比较大,是因为初始记忆时间较短造成的。虚线Nt=10 000与点划线Nt=30 000能很好地逼近原始定义数值解。这说明初始记忆时间越长所取得的数值解越精确。从计算量上来看,Nt=3 000,Nt=10 000,Nt=30 000时,最后一步参与计算的时刻点数分别为8 600项、23 000项和59 000项。可以看到三种情况计算量均比原始定义方法少得多,另外也可以得到初始记忆时间越长所得结果越精确的结论。 图6 三种数值解(原始定义、短记忆原理和改进的短记忆原理)Fig.6 Three numerical solutions (original definition, short memory principle and improved short memory principle) 图7 两种短记忆原理方法与原始定义方法间的误差Fig.7 The error between the two short memory principle methods and the original definition method 图9给出了相同的步长和截断项数,不同的的步长放大倍数下,数值解与原始定义之间的误差情况。其中实线、虚线和点划线分别为放大5倍、10倍和20倍的结果与原始定义数值解的误差。可以看到在放大20倍时误差较大,这与表二的结果吻合。另外,放大5倍与放大10倍时相比,误差并没有相应的减少太多。这从表二中也能看出来,两次放大的影响系数与各自对应的放大倍数都很接近。计算量上,n=5,n=10,n=20时最后一个时间步参与计算的时刻点数分别为10 400项、8 600项以及6 950项。放大5倍的计算量比放大10倍大了不少,但是精度却并没有提升太多。但是放大10倍与放大20倍相比,其所增加的计算量和误差的减小是符合我们期望的。 图8 改进的短记忆原理方法(步长同为h=0.000 1,放大倍数同为n=10,不同的截断项数Nt)与原始定义方法间数值解的误差Fig.8 The error of the numerical solution between the improvedshort memory principle method (the step size h=0.000 1 and magnification factor n=10 are the same, and the number of truncation items Nt are different) and the original definition method 图9 改进的短记忆原理方法(步长同为h=0.000 1,截断项数Nt=3 000,不同的放大倍数n)与原始定义方法间数值解的误差Fig.9 The error between the improved short memory principle method (the step size h=0.000 1 and the number of truncation items Nt=3 000 are the same,and magnification factors n are different) and the original definition method 工程中的真实动力系统几乎总是含有各种各样的非线性因素。Duffing方程是机械振动学、物理学、生物学和神经学等领域广泛应用的数学模型。具有分数阶阻尼的Duffing系统为 (10) 分数阶数α=0.5,时间步长均取h=0.001,计算1 000 s,截取后700 s。式(10)分别采用4阶龙格库塔法和改进的短记忆原理方法进行求解。龙格库塔法的位移曲线如图10(a)所示。短记忆原理方法的截断项数为Nt=10 000,步长放大倍数为n=5。计算结果的位移曲线如图10(b)所示。从位移图上看两者的结果很相似,然后再看两种方法的系统相图,如图10(c)和图10(d)所示。从位移图和相图上看,该改进的短记忆原理方法能很好的模拟分数阶非线性系统。 图10 分数阶Duffing方程的位移图和相图分别用龙格库塔法和改进的短记忆原理方法Fig.10 The displacement diagram and phase diagram of the fractional Duffing equation use Runge-Kutta method and improved short memory principle method respectively 分数阶Lorenz系统是一个典型的多自由度混沌系统。简化的Lorenz系统只含一个系统参数,其方程为 (11) 系统参数设定为c=10。分数阶数α,β,γ均取0.98。用预估校正法与改进的短记忆原理方法计算50 s,时间步长均取h=0.001,取后40 s数值结果进行比较,如图11所示。可以看到,改进的短记忆原理方法能很好地模拟多自由度系统。 图11 分数阶Lorenz混沌吸引子部分相图预估校正法和改进的短记忆原理方法Fig.11 Fractional Lorenz chaotic attractor partial phase diagram prediction correction method and improved short memory principle method 在数值计算中通常采取减小步长来获取高精度数值解,而分数阶导数具有记忆性,每一个时刻都与前面所有时刻相关,所以减小步长的同时会带来巨大的计算量。经典的短记忆原理,在减少计算量上有很大贡献,但是造成的误差不可忽视。本文提出一种基于Grünwald-Letnikov定义的改进的短记忆原理方法,并应用于分数阶阻尼振动方程、分数阶非线性Duffing方程和分数阶Lorenz混沌系统。分数阶阻尼振动方程的解通过与经典的短记忆原理方法相比,改进的短记忆原理方法能极大的减小误差,并且没有增加计算量。通过分数阶非线性Duffing方程的算例,说明该方法也适用于模拟非线性系统。改进的短记忆原理方法应用于Lorenz混沌系统也有很好的数值结果。在改进的短记忆原理方法中,即使减小步长提高精度,也不会带来很大的计算量的变化。在使用改进的短记忆原理方法时,截断项数在计算机和时间允许的情况下尽可能取得更大,而放大倍数的选取可通过计算得到的影响系数与放大倍数匹配。

3 算例分析
3.1 分数阶阻尼受迫振动

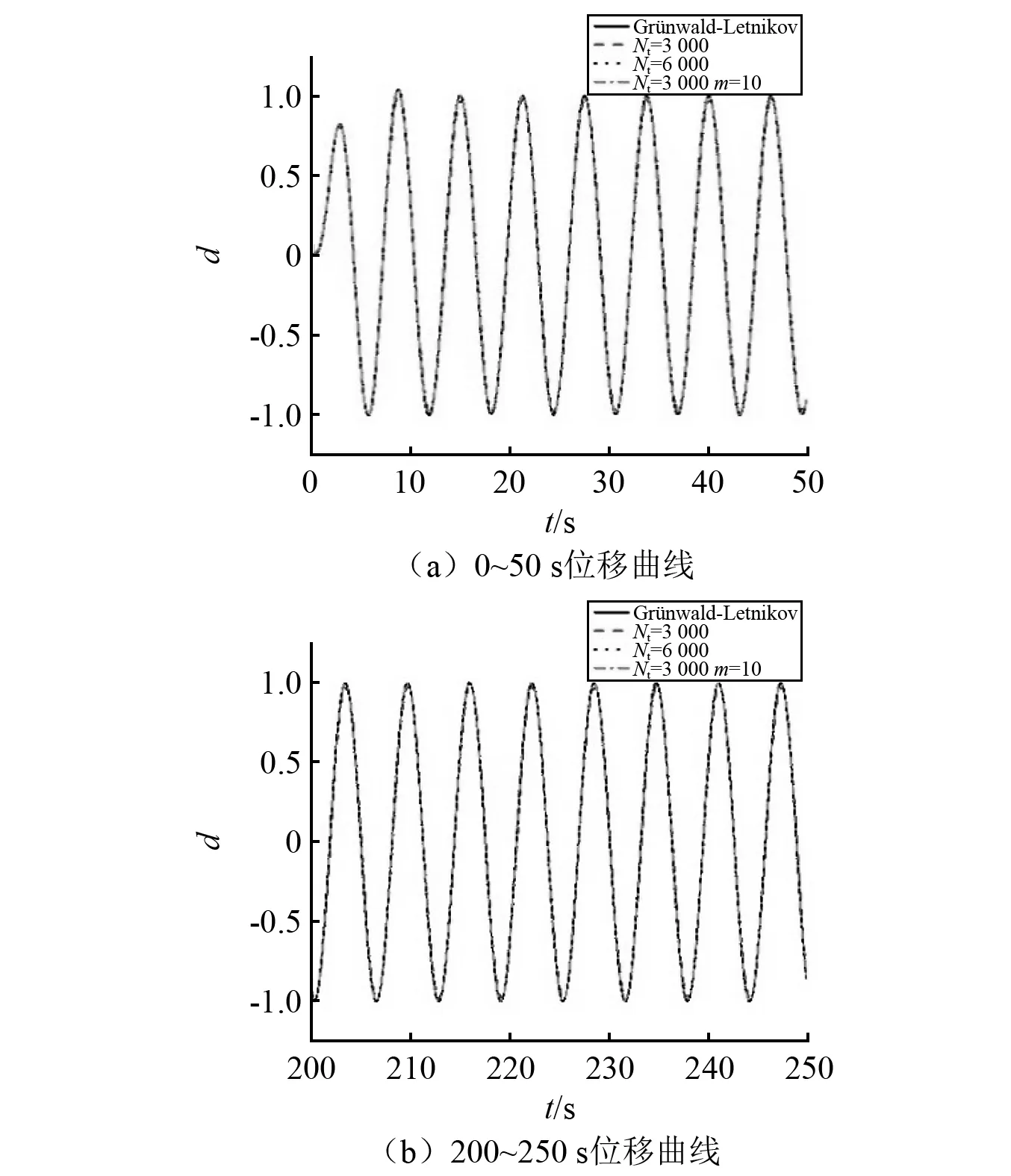
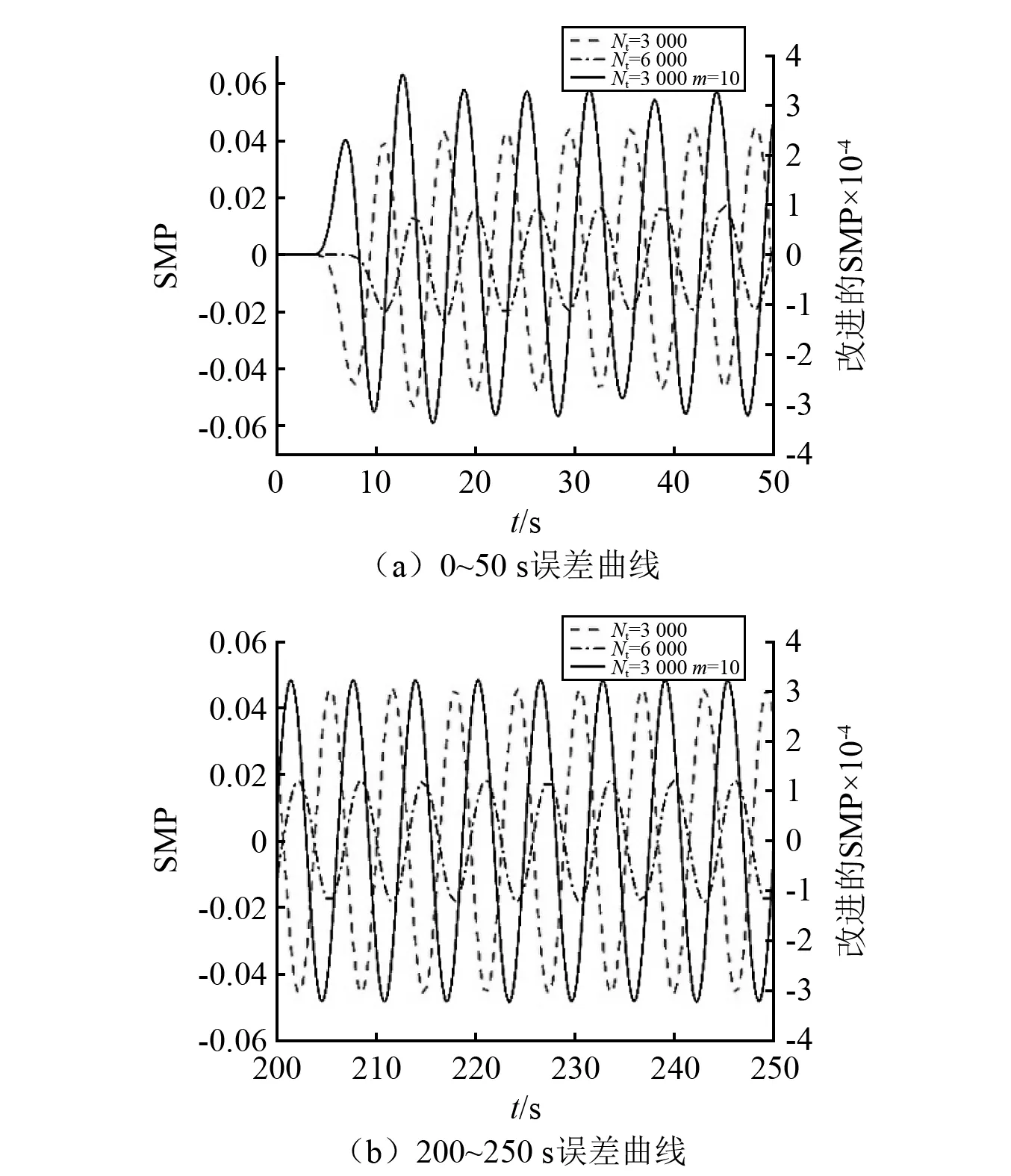

3.2 分数阶非线性Duffing方程

3.3 分数阶Lorenz混沌系统
4 结 论
