以概念构图促进深层理解——《圆的认识》一课教学实践与思考

□ 胡佳萍 韦 丹

《圆的认识》是一节概念课，这节课中涉及的概念比较多。教学中教师要关注学生学习后能否主动建立起这些概念之间的联系。指向理解进阶的概念构图教学，可以充分把原本不可见的学生的理解状态、思考路径、思维方法呈现出来，促进学生的数学理解，帮助他们形成新的认知结构。基于上述思考，我们设计了如下教学路径（如图1）。

图1

一、自学教材，初学构图，呈现经验性理解

学生通过自学，对“圆”会形成一种个性化的理解，有了初步的认识。这时可请学生基于经验性理解进行初步概念构图。教师分析这些作品，按“概念缺失化呈现”“概念零散化呈现”“部分概念联结化呈现”这三种情况进行分类整理（如表1）。

表1 学生经验性理解的不同类型

续表

从表1可以发现，学生的概念理解水平呈现散点形态，缺乏内在关联的理解。由此确定本节课的重点：借助概念构图帮助学生建立概念联结，提高学生的概念理解层次。

二、借助材料，互学论图，形成衍生性理解

在学生已有经验的基础上，针对性地设计了两个活动。一是画圆操作，促进学生理解概念之间的关系；二是比较史料，揭示圆的本质。这两个活动能帮助学生逐步感悟圆的本质，达到“明晰联系、抽象本质”的目标。

（一）操作中明晰联系

师：每位同学都准备了圆规，你能用圆规在纸上画一个圆吗？你能在圆中标出一条半径和一条直径吗？大家先自己试试看。

（学生动手操作）

生：我按牢针尖，旋转铅笔就画出了一个圆。圆心到圆上的距离就是一条半径，再延伸下去就是一条直径。

生：我先确定一个点作为圆心，再把圆规两脚间的距离作为半径，针尖不动，铅笔旋转一圈。直径是两端都在圆上的，所以穿过圆心再画一条线段就是直径。

师（小结）：连接圆心和圆上任意一点的线段叫作半径，一般用字母r表示；通过圆心并且两端都在圆上的线段叫作直径，一般用字母d表示。

师：刚才同学们介绍的画圆方法，有什么相同的地方？

生：都是绕着圆心画一条曲线。

生：曲线离圆心的距离不能变（也就是曲线上的点离圆心的距离不能变）。

师（小结）：圆上任意一点到圆心的距离都不变。

师：你还有别的发现吗？

生：半径可以画无数条，同一个圆里半径都相等。

生：一条直径由两条半径组成，所以直径是半径的2倍。

生：圆规两脚间的距离越大画出的圆越大，圆规两脚间的距离越小画出的圆越小，因此半径决定圆的大小。

生：圆心的位置不同，圆的位置就不同，因此圆心决定圆的位置。

师（小结）：通过刚才的活动和讨论，我们知道了因为圆心决定圆的位置，所以在画圆时针尖不能动；因为半径决定圆的大小，所以画圆时圆规两脚间的距离不能变。

师：通过刚才的学习交流，你对原来的构图有什么修改或补充？

生：我把图（如图2）画得太简单了，我可以再补充直径、半径和圆心的字母式以及它们的特征。

图2

生：在我的图（如图3）中，我把书本上讲到的所有知识都像一个圆圈一样发散开。自己动手画圆之后，我发现圆心决定位置，半径和直径决定圆的大小，因此我会再调整这个概念图的位置和顺序。

图3

生：通过自学书本，我知道了圆心、半径和直径分别用什么字母表示，通过画圆，我了解了这三者的数量以及它们的特征，接下去我会对作品（如图4）做一些修改，把概念间的关系表达得更加清晰。

图4

借助画圆的过程，学生完善了脑海中缺失的概念，深刻体会到各概念之间的关系，让概念构图从“原来的零散概念”走向了“概念之间的联结”。例如，从“半径”这个概念走向“半径的定义（半径是连接圆心和圆上任意一点的线段）”“半径的特征（半径有无数条，并且半径决定圆的大小）”“半径与直径的关系（在同圆或等圆中，直径是半径的2倍）”。学生自主修正和完善概念之间关系的过程，就是慢慢走向深度理解的过程。

同时，在这个过程中，学生也更加深刻地感悟到“圆是一条曲线”的本质属性，明白“定点”和“定长”是圆的特别之处。但这时让学生来描述什么是圆，无疑是较烦琐的或者是不精准的，因此，引入史料进行对比学习是帮助学生建立知识联结的助推器。

（二）比较中抽象本质

教师呈现我国古代名著《墨经》中的这样一句话：圆，一中同长也。

师：怎么理解这句话呢？

生：一中指的是“一个圆心”，同长指的是“半径有无数条且相等”和“直径有无数条且都相等”。

生：其实用圆规画圆也是遵循“一中同长”的原理，一中指的是针尖，同长指的是圆规两脚间叉开的距离都相等。

生：圆是一条曲线，曲线上的每一个点与圆心都保持相等的长度。

师：把《墨经》中的“圆，一中同长也”放到我们的概念图里，可以吗？你会怎么完善概念图？

对史料的解读和比较，可以让学生更深刻地体会到圆的本质，即圆是一条“一中同长”的曲线。由此学生将用圆规画圆的动作、圆的三要素特征、《墨经》中“一中同长”这三种不同的表征方式有效关联起来，形成丰富、深入、抽象的概念理解。

三、把握整体，合学正图，完善结构化理解

学生在弄清了各概念之间的联系、明晰了圆的本质后，依旧不一定能将其理解清晰、有序地表示出来。这时，教学进入“合学正图”阶段，即让学生通过讨论、合作等方式来完善理解，对已有概念图进行修正或重构，如补充、关联、提炼等。学生在这个过程中会呈现出不同的理解成果，不断地深化理解。

师：现在请你带着自己的理解与小组成员一起讨论如何修改概念图。可以在原来构图的基础上修改，也可以重新构图。

（小组讨论后合作构图）

生：我来解释一下我们小组的作品（如图5）。我们认为圆有圆心、半径和直径三要素，所以把这三者放在圆的后面，加上连接词就能把这些概念之间的关系说得更清楚了。它们都有自己的特征，如圆心用字母O表示，只有1 个，它决定圆的位置。半径和直径也有自己的特点。

图5

生：我们组认为应该把“直径”和“半径”放在同一边，“圆心”放在另一边（如图6）。因为它们的特点完全不同，也没有联系。同时，把无数条且都相等和半径、直径决定圆的大小这两个共同特征，放在“直径”和“半径”这一边。

图6

生：听了前面同学的讨论，我认为在构图的过程中还可以增加一些东西，比如直径与半径的联系、画圆的方法等。我还想到，圆心是直径的中点，也是半径的端点，因此还可以继续深挖这些概念间的联系。

“正图”这个动态修正的过程可以促使学生不断自主学习、深入思考、求联求通。概念构图以图促思，其实质是把理解外化，这有利于学生完善认知结构，发展元认知，形成具有一定层级关联的数学理解。

四、联系生活，拓学用图，促进抽象性理解

拓学用图是学生在理解了圆的本质、形成了结构化理解之后，检验自己能否自觉运用这些理解来解释生活中的现象或概念的过程，是教学时不可忽视的环节。在此环节中设计了两个研究任务（如图7），以帮助学生应用和拓展，进一步强化理解，从而形成抽象、精练的认知。

图7

师：我们先来看任务1，你能解释它们为什么都是圆的吗？

生：圆形车轮滚动时，车轴离地面的距离始终相等，更平稳。

生：围着圆桌吃火锅，所有人与火锅的距离都相等，更方便。

生：围成圆形的套圈游戏，所有人离红旗的距离都相等，更公平。

师：这些现象中体现了圆的什么知识？

生：同一个圆里所有的半径都相等。

生：圆上任意一点到圆心的距离都相等。

师：我们再来看任务2，“生活中我们经常这样描述圆”，你觉得这些描述都准确吗？

生：硬币的形状或者说轮廓是圆的。

生：没有角的图形不一定是圆。

生：前面我们已经学过，圆的本质是一条“一中同长”的曲线，在概念构图上也清晰地体现了这一点，而球是立体图形，所以不能说球是圆形的。

师：通过刚才的研究，你能根据自己的收获进一步修改构图吗？

（学生第三次修改构图，教师呈现学生作品，如图8和图9）

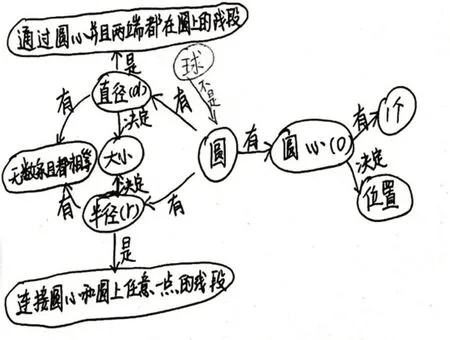
图9

以上，学生借助解释和应用的过程，深化对圆的本质的理解，以完善知识结构。在这个过程中，思辨贯穿始终，突出体现了学以致用和以用促学的教学理念，学生在概念理解和数学思维方面都得到了很好的发展。

总之，概念课的学习要理解概念的本质，要重视概念间的联结。概念构图很好地把学习主动权还给了学生，使学生从“被动、接受、操练”转变为“主动、探究、思辨”，让思维可视化、概念具象化、知识结构化。