借概念构图 促整体建构——以《因数与倍数》整理与复习课为例

□ 何叶飘 黄鼎滴

整理与复习课主要有两个目标，即知识整理和巩固提升。在整理与复习课上，要通过对知识间关系的梳理，点串成线，线连成面，帮助学生实现知识结构化、系统化。以往教师在进行“因数与倍数”单元的整理与复习时，通常先引导学生梳理归纳知识点，形成结构，然后以不同类型、不同层次的练习为载体，通过训练、讲评来检测学生对知识的掌握情况。但这一单元教学内容中，涉及的概念数量多，概念比较抽象，概念间的关系复杂，导致学生整理时容易出现混乱现象。针对这种现状，笔者尝试以“概念构图”为教学途径，引导学生在合作构图中不断修正、完善概念理解，进一步明晰概念之间的内在关系，提高理解水平和应用能力，实现深度学习。

一、初构概念图，呈现已有经验

为更好地了解学生对于因数、倍数知识掌握的情况，教师请学生回忆“关于因数和倍数，你能想起哪些知识点”，思考“这些知识点之间有什么联系”，并在导学单上绘制概念图。学生在这一过程中，会充分暴露已有的认知状态。教师通过整理学生的作品（如图1~图4）发现，学生的理解水平存在很大的差异。

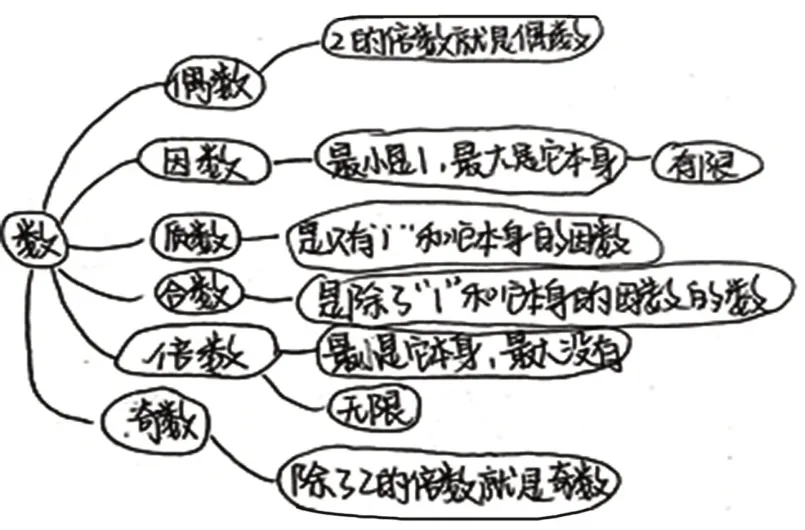
图1 作品1

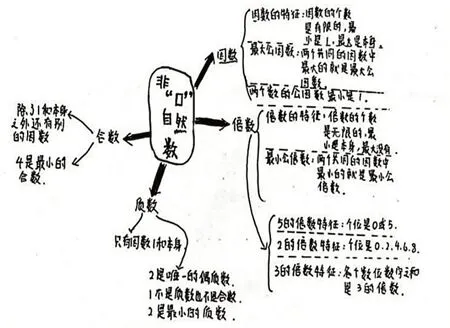
图2 作品2

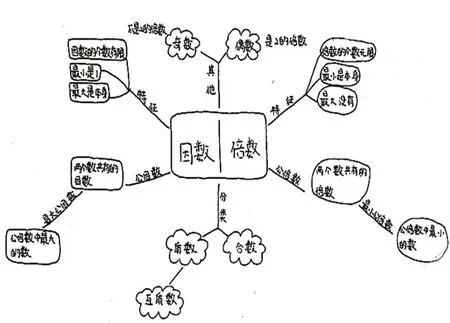
图3 作品3

图4 作品4

从以上作品中可以看出学生的三个理解水平层次。

理解水平1：作品1 和作品2 都是从“数”这个主干生长出“奇数、偶数”“质数、合数”“公因数”“公倍数”和“互质数”等分支。这部分学生只是对知识点进行了简单的罗列，层级关系不清晰，知识结构较低。因此我们把它们定位为理解水平1。处于这一水平层次的学生占全班总人数的22.2%。

理解水平2：从作品3 可以清晰地看出“因数、倍数”是一级概念，“奇数、偶数”“质数、合数”是从属于“因数、倍数”的二级概念，有一定的层级关系。虽然有些层级关系表达得还不够清晰，但对比作品1和作品2，已经高了一个水平，我们把它定位为理解水平2。处于这一水平层次的学生占全班总人数的71.1%。

理解水平3：作品4 不仅能清晰地表达不同维度的知识，而且有序地建构了各个概念之间的层级关系，并能准确地表达“因数和倍数”是相互依存的关系。处于这一水平层次的学生较少，只占全班总人数的6%。

由此可以看出，学生对“因数与倍数”单元中涉及的知识点都能一一罗列，但缺乏概念间的内在关系的梳理，只有小部分学生能厘清概念间的层级关系。因此在教学中教师要对学生已有认知进行深度剖析，强化对零碎概念的整理与关联。

二、评论概念图，经历深度辨析

教师选择作品3作为主要讨论对象，引导学生进行论图辨析。

1.教师出示问题一：你能看明白作品3吗？你看明白了什么？请学生讨论。

生：我能清晰地看到因数和倍数的特征，最大的因数是其本身，最小的倍数也是其本身。

生：我发现在“因数与倍数”的相关知识中有很多概念，这些概念存在着一定的联系。

2.教师出示问题二：这些概念之间的层级关系是否合适？如果不合适，你会怎么调整？请学生讨论。

生：我觉得质数和合数应该放在因数的层级之下，因为根据因数的个数，可以把非零自然数分成质数、合数和1，作品3的作者把1漏了。

生：我还有补充，质数和互质数是不一样的，质数是根据因数的个数来判定的，它是一个数。互质数是根据公因数的个数来判定的，它是两个数之间的一种关系。所以，互质数应该在公因数的层级之下。

生：我还有点想法，我觉得奇数和偶数应该放在倍数的层级之下，因为奇数和偶数是根据“2 的倍数特征”来判定的。

生：我有不同意见，奇数和偶数也可以放在因数的层级之下，因为可以根据有没有因数2来判定奇数和偶数。

……

之所以选择作品3展开讨论，首先是因为它代表着大部分学生的理解水平。用它来引导学生展开讨论和思辨，具有一定的普适性，容易激发学生的学习积极性和主动性。其次是因为作品3 里有比较适合激发学生思辨的切入点，学生思维生长的空间比较大。比如“奇数、偶数”这两个概念，学生把它们放在“因数与倍数”总概念之下，连接词是“其他”，就说明他对“奇数、偶数”应该放在哪个层级之下并不清楚。因此在课堂中，应紧扣学生的认知困惑点，让学生在交流、辨析、调整的过程中，不断理解“奇数、偶数”与“因数、倍数”概念之间的关系。厘清了这些概念之间的层级，也就厘清了各个概念之间的区别与联系。另外，我们也从作品3中发现，学生对“质数”和“互质数”这两个概念的理解比较模糊。“质数”与“互质数”之间的辨析，需要透过表象看本质，因此可以通过质疑与释疑来促进学生深入理解它们的意义。

在交流过程中，学生以图为介，边观察边思辨，在思维碰撞中形成深度的理解。学生有的从概念定义的角度对“质数”和“互质数”进行了辨析；有的拓宽了对“奇数、偶数”由来的再认知，启发其他同学感悟“如何从不同视角把握知识间的关系”。通过这样的过程，学生不再简单地从字面上理解数学概念，而学会进一步沟通概念之间的联系，以此来深入理解概念的意义。

三、重构概念图，完善认知建构

学生掌握了“因数与倍数”的相关知识及内在关系后，还需要在理解的基础上通过反思进行重构，以达到内化提升的目的。因此在这个环节安排了两个学习任务：（1）在小组内交流各自的收获和思考。（2）以小组为单位重构“概念图”。

在小组合作中，学生可以从构图的形式和理解的内容两个维度出发，通过比较、思辨、修正、完善等数学活动，达成共识，形成层级关联清晰的知识结构。这是数学内化的最好表现，也是学生学会表达、强化理解的有效途径。

通过这样一个重构的过程，学生对奇数与偶数的处理进入“柳暗花明又一村”的境界。有些学生把质数和合数放在了因数个数有限的特征之下，可见他们对质数和合数已经有了正确的个性化理解。这个过程让学生不再把这些概念理解成“数”，而是明白了它们的本质意义，并建立了符合自己认知特点的层级关系。学生的理解从“散乱”走向了“结构”，从“表层”走向了“深刻”。

实践证明，学生经历了“初构概念图—评论概念图—重构概念图”的过程，就会自主产生很多新的感悟，形成一些更深刻的数学理解。可见，概念构图在整理与复习课中的运用是有效的，值得应用推广。但需要强调的是，教师在组织教学时至少要做到以下三点：一是遵循学生“从发散思维到结构思维”的学习导向来进行教学；二是加强“思维可视”为“理解进阶”服务的意识；三是把握“求同存异”与“深层关联”的教学价值。相信唯有如此，概念构图在整理与复习课中的运用才会唤醒学生的数学思维活力，有效提升他们的数学理解水平，为实现“轻负高质”提供可行路径。