基于改进粒子群算法的机器人时间最优轨迹规划

程浩田 ，祝锡晶 ，黎相孟 ，赵 晶 ，冯琪渊 ，丁帅帅

（1.中北大学 机械工程学院，太原 030051；2.先进制造技术山西省重点实验室，太原 030051）

0 引言

随着企业生产规模的扩大和自动化水平的提高，人类对机器人的工作效率提出更高的要求，并且要求机器人能够按照预定的轨迹平稳运行，因此机器人轨迹规划的好坏对其能否稳定高效的运行起着至关重要的作用。于是，轨迹优化应运而生。轨迹优化通常可以分为2种：一种是时间优化；另一种是能耗优化［1］。其中，时间最优轨迹规划在提高机器人的工作效率和增加产能输出等方面有着重要的实际意义，一度成为了研究热点。

国内外学者做了大量深入的研究，李国洪等［2］提出一种改进遗传算法与7次B样条曲线相结合的轨迹优化算法；李林升［3］运用惩罚函数法对关节运行轨迹进行了时间优化；陶庆等［4］提出一种新型烟花算法用于求解不同速度约束条件下机械臂轨迹运行的最短时间；XU等［5］利用神经网络算法和模糊控制算法对轨迹进行了时间优化；HE等［6］利用免疫算法同时对时间和能耗进行了优化。虽然其中一些方法被证明具有一定的实际应用价值，但是仍然存在诸多问题需要解决，如求解困难、计算量大以及局部最优。粒子群算法作为一种新兴的群体智能算法［7］，因其具有强大的全局搜索能力、较少且易调整的参数以及简单的速度—位移模型等优点，被广泛应用于寻优问题。

在对机器人进行轨迹规划时，传统的三次、五次多项式插值函数已经无法满足要求，所以将其结合起来组成“3-5-3”混合多项式插值函数，该函数可以弥补三次多项式插值规划时角加速度突变和五次多项式插值规划时角速度较大的问题。本文综合考虑机械臂各关节角速度、角加速度以及动力学等约束条件，首先采用动态变化学习因子策略对粒子群算法进行改进；然后在此基础上选择“3-5-3”混合多项式轨迹规划的总时间t作为单目标进行优化；最后在MATLAB仿真环境下验证改进算法的优越性和有效性，以达到时间优化的预期目标。

1 混合多项式插值函数的构造

本文采用“3-5-3”混合多项式插值函数进行机器人关节空间轨迹规划。该方法将预先设置的4个路径点分成3段，每段均由相邻的2个路径点组成，且第1段和第3段采用三次多项式插值函数进行规划，第2段采用五次多项式插值函数进行规划。机器人末端执行器在经过3个区间时，所花费时间分别为t1、t2、t3，其函数表达式：

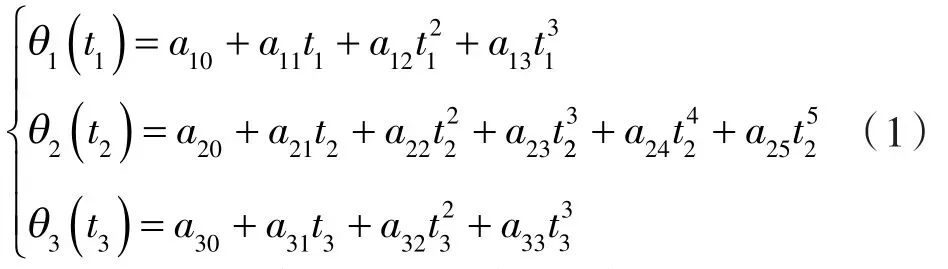
对式（1）求导，可分别得到各段角速度、角加速度表达式，根据每段起始点和终止点的约束条件，分别求得混合多项式共14个系数。

2 改进粒子群算法的设计

粒子群算法起源于鸟类的捕食行为，其原理：首先将粒子群初始化；然后使粒子通过追踪2个极值而不断更新自己，一个是个体极值，它是粒子本身当前所能找到的最优解，另一个是群体极值，它是整个粒子群体当前所能找到的最优解［8］；最后让粒子群迭代，重复上述过程，直到达到终止条件。其速度和位置更新公式如下：

式中 ω ——惯性权重；

c1、c2——学习因子；

r1、r2——随机常数，变化区间为［0，1］；

pid—— 粒子i最优位置pi在第d维中的分量［9］；

pgd—— 粒子群最优位置pg在第d维中的分量。

本文引入动态学习因子c1、c2，预先设定c1、c2最大值相等，然后使c1值随着搜索次数的增加慢慢减小，c2值随着搜索次数的增加慢慢变大，保证粒子群算法在运行初期具备较强的全局搜索能力，维持种群的多样性。而在算法运行后期则强化粒子局部搜索的能力，从而提高搜索精度，并加快粒子的收敛，便于其在短时间内找到全局最优。其表达式：

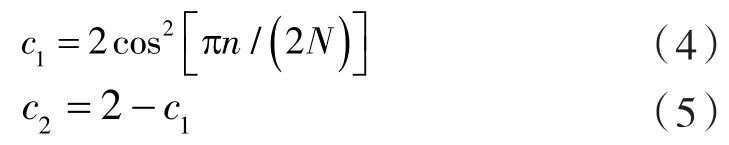
式中 n ——当前迭代次数；

N ——总迭代次数。

因为是针对机器人进行时间最优轨迹规划，所以在进行轨迹优化之前确立时间为优化目标，其适应度函数如下［10］：

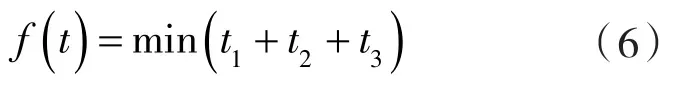
3 MATLAB仿真验证

规划机械臂末端执行器从初始点A经过中间点B、C到达终止点D的时间最短运行轨迹。各路径点分别对应各关节角度如表1所示。

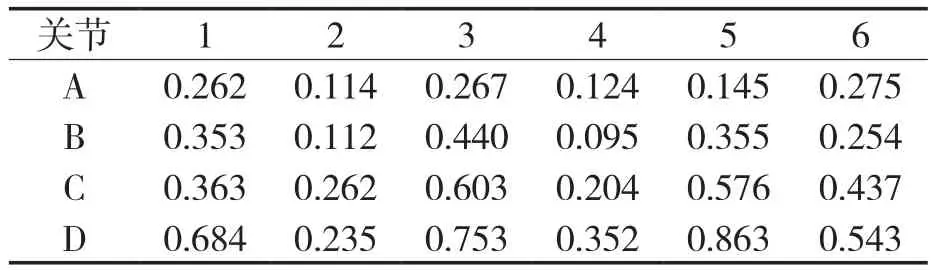
表1 路径点A、B、C以及D所对应的各关节角度Tab.1 Joint angles corresponding to path points A，B，C and D （单位：rad）

在进行优化时，考虑机器人实际工作条件，粒子的速度和加速度不得超过机器人的正常工作范围，约束条件如式（7）所示［11］：

预先设置粒子种群m为30，初始位置为［0，10］，各个关节最大转动速度 Vmax分别为 4，4，5，7，6，11 rad/s，最大加速度 amax为 10.0 rad/s2，各个阶段时间的迭代初始值为2 s，迭代次数N为500。分别采用标准粒子群算法与改进粒子群算法进行规划［12］。经过MATLAB仿真，具体收敛次数和完成时间如表2所示，改进粒子群算法优化后的“3-5-3”混合多项式各个阶段时间如表3所示。

表2 不同学习因子下各关节收敛次数、时间对比结果Tab.2 Comparison of convergence times and convergence time of each joint under different learning factors

表3 改进粒子群算法优化后的各个关节轨迹分段运行时间Tab.3 The segmented running time of each joint trajectory optimized by improved particle swarm optimization algorithm （单位：s）

由表2可以得出，经过改进粒子群算法优化后的各关节局部收敛时间和全局收敛时间均优于标准粒子群算法，局部收敛速度大大提高［13-16］，并且在运行初期维持了种群多样性。由此可以验证改进粒子群算法良好的优越性［17］。

为保证机器人各个关节的粒子在优化过程中全部完成迭代，达到终止条件，需要选取不同关节在3个阶段中分别所耗费的最大时间。通过分析表3，可得到各个阶段运行时间最大值：t1=1.319 6 s，t2=1.994 0 s，t3=1.164 s，总时间为 4.42 s，与未经优化单纯利用的“3-5-3”混合多项式进行轨迹规划的迭代初始值相比，缩短了1.58 s，证明了改进粒子群算法的有效性。

为验证优化后得到的各个阶段时间是否满足机器人轨迹规划的基本要求，通过t1、t2、t3对机器人再次进行“3-5-3”混合多项式关节空间轨迹规划，得到各关节角位移、角速度以及角加速度随时间变化的曲线分别如图1～3所示，运行过程中角位移、角速度、角加速度最大值如表4所示。

图1 各关节角位移曲线Fig.1 Angular displacement curve of each joint

图2 各关节角速度曲线Fig.2 Angular velocity curve of each joint

图3 各关节角加速度曲线Fig.3 Angular acceleration curve of each joint

表4 运行过程中产生的最大值Tab.4 Maximum value generated during operation

由图1～3分析得出，机器人各关节角位移、角速度以及角加速度曲线平稳连续且无突变，说明优化方案可以保证机器人在整个运行过程中维持平稳的状态，能很好地通过每一个路径点，发挥其良好的工作性能。由表4可以得出机器人在运行过程中产生的最大值均满足速度和加速度约束条件，验证了改进算法的可行性。

4 结语

本文以六自由度工业机器人为研究对象，针对其时间最优轨迹规划问题，提出一种采用动态学习因子策略的改进算法。仿真结果表明，改进算法全局收敛速度和局部收敛速度均优于标准粒子群算法，且与未优化的“3-5-3”混合多项式轨迹运行时间相比缩短了26%，优化后的轨迹同时满足机器人的关节位置、速度以及加速度约束，验证了改进粒子群算法的优越性、有效性以及可行性。