不可压磁流体力学方程的整体解与衰减估计
2022-05-20王朋杰
张 洁,王朋杰
(贵州师范大学 数学科学学院,贵阳 550025)
0 引 言
考虑下面的三维不可压磁流体力学方程组:
(1)
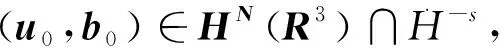

a.∇kf表示k阶空间导数, 定义为:
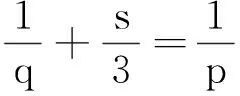
证明参考文献[9]。
主要结果如下:
定理1令(u0,b0)∈HN,N≥2,并且存在一个常数 δ,有
‖u0‖H2+‖b0‖H2≤δ
则柯西问题方程组(1)存在唯一的整体解(u,b),使得∀t≥0,有
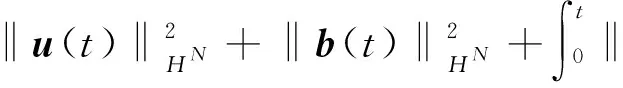
并且对于l=0,1,…,N有以下的衰减结果:
(2)
注1将如上衰减与文献[8-10]比较时, 容易知道在证明整体解存在性时只要求(u0,b0)的H2范数小, 但不需要H3范数足够小。与此同时在证(2)和(3)时, 也不要求(u,b) 的高阶导数估计。
1 能量估计
在这一节中, 将推导出 (u,b)的低阶和高阶的能量估计。
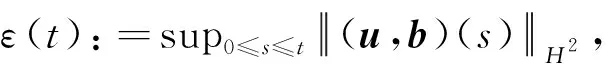
引理1令(u0,b0)∈HN,N≥2, 且(u,b)为柯西问题方程组(1)的解, 则
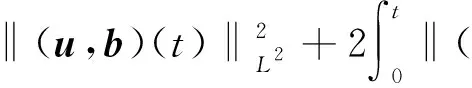
(3)
证明将方程组(1)的第1,2两个式子分别乘上u和b,然后加起来并且运用分部积分即得.
引理2令(u0,b0)εHN,N≥2, 且(u,b)为柯西问题方程组(1)的解, 有
(4)
证明将∇k作用在方程组(1)上, 然后在所得等式两边乘上(∇ku,∇kb)并在R3上运用分部积分, 有
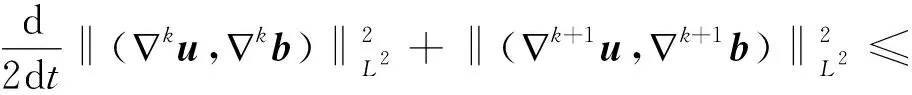
‖∇k(u·∇u,b·∇b)∇ku‖L1+‖∇k(u·∇b)∇kb‖L1+‖∇k(b·∇u)∇kb‖L1=M1+M2+M3
(5)
接下来将对上述M1~M3项进行估计。对于M1项,因u·∇u与b·∇b的形式相同,所以只需估计 ‖∇k(u·∇u)∇ku‖L1。
‖∇k(u·∇u)∇ku‖L2≤C‖∇k(u·∇u)∇ku‖L6/5‖∇k+1u‖L2
(6)
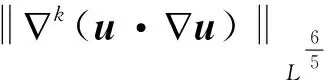
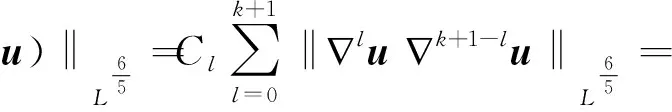
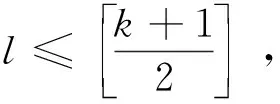
(7)
这里α,θ需满足条件:
(8)
使用类似的方法, 有估计
(9)
所以, 由(7)式和(9)式, 有
(10)
再结合(6)与(10)有
(11)
类比于(11)式, 对‖∇k(b·∇b)∇ku‖L1这一项, 有
(12)
联合(11)和(12)式, 有
(13)
注意到在(7)式后面的两个估计中,若将u替换为b其结论自然是成立的,有
(14)
(15)
再根据(13)-(15),即得(4),即完成引理2的证明.关于解的全局性,令
T*=sup{T:‖(u,b)(t)‖H2≤2‖(u0,b0)‖H2},可以断言,如果‖(u0,b0)‖H2小的话,那么对∀t<+∞,有 ‖(u,b)(t)‖H2≤2‖(u0,b0)‖H2否则, 取‖(u0,b0)‖H2=ε,使得1-4C(ε2+ε)>a>0, 由T*的定义,它大于零.然后根据引理2, 将(5)式从0到T*积分,有‖(u,b)(T*)‖H2≤‖(u0,b0)‖H2,显然矛盾。进一步,如果‖(u0,b0)‖H2≤ε,同时∇k(u0,b0)εL2,那么对于kεN+,有
(16)
对∀t>0,将(16)从 0 到t积分, 有
‖∇k(u,b)(t)‖L2+‖∇k+1(u,b)‖L2((0,t)×3)≤C‖∇k(u0,b0))‖L2。
(17)
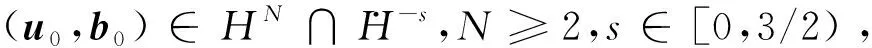
‖(Λ-su,Λ-sb)(t)‖L2≤C0
证明将Λ-s作用在方程组(1)上,把所得的结果乘以 (Λ-su,Λ-sb),然后在R3上积分,有
‖Λ-s(u·∇b)Λ-sb‖L1+‖Λ-s(b·∇u)Λ-sb‖L1=
T1+T2+T3+T4
(18)
接下来估计T1~T4,对于T1
|T1|≤‖∇-s(u,∇u)∇-su‖L1≤
C‖∇(u,∇u)(t)‖L1/2+s/3‖∇-su‖L2≤
C‖u‖L3/s‖∇u‖L2‖∇-su‖L2
(19)
类似有

(20)
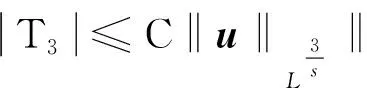
(21)
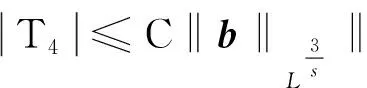
(22)
根据(18-22)式,再结合估计b式, 有
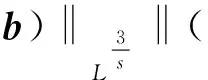
(23)
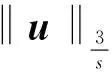
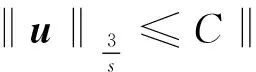
C(‖∇u‖L2+‖∇2u‖L2),s∈[0,1/2)
联合(23)式, 有
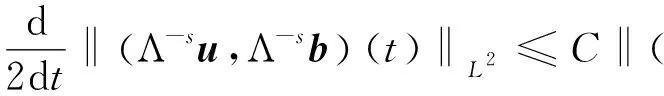
再结合(17)式, 最后有
‖(Λ-su,Λ-sb)(t)‖L2≤C,s∈[0,1/2)
(24)
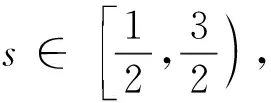
(25)
根据(24)和(18)式,有
(26)
解这个微分不等式,有
(27)
(28)
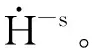
‖(u,b)‖L2≤(1+t)-1/4
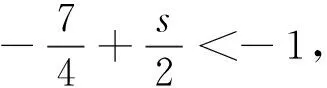
证完。
3 证明定理1