基于半随机滤波的线性退化设备剩余寿命预测

朱 旭，司小胜，胡昌华，莫仁鹏

(火箭军工程大学，西安 710000)

0 引言

随着工程实际中设备复杂度的不断增高，系统因故障失效导致的损失也变得愈发不可承受，严重的设备故障不仅会造成经济损失，甚至会产生人员伤亡。因此，追求更高精度的设备剩余寿命预测，成为提高设备可靠性和安全性、进行合理的视情维修的关键。

现有的剩余寿命(RUL)预测研究，主要针对军事装备[1]、锂电池[2]、大型民用机械(如船舶柴油机)[3]等设备，由此发展出了基于机理模型的方法、基于机器学习的方法和统计数据驱动的方法。其中，统计数据驱动的设备剩余寿命预测方法中研究最多的是基于随机退化过程建模的方法，这类方法由于基于概率论和随机过程理论，通过预测设备性能退化变量到达失效阈值的时间实现剩余寿命的预测，具有良好的数学性质和统计特性，能够较准确地描述设备退化和寿命分布的数学特征，因而得到了广泛的应用。在最新的研究中，针对随机退化设备剩余寿命预测问题已经拓展到两阶段[4]、非线性[5]、多重不确定性[6]和多源信息融合[7]等情形。然而，当前的研究普遍未能解决失效阈值如何确定的问题。尽管最近的研究中提出了随机失效阈值[8]和多环境实验[9]等方法，但对失效阈值的确定仍然依赖退化实验，并且这些方法通常只考虑了历史监测信息，难以将失效数据有效地应用于剩余寿命预测模型的建立。

在统计数据驱动的剩余寿命预测方法之中，文献[10]提出的半随机滤波方法不需要失效阈值的相关信息，可以充分利用失效数据，并基于贝叶斯滤波理论将历史监测信息应用于剩余寿命预测模型的建立，因此在应用中具有明显的优势。然而，该方法预测精度受制于半随机滤波模型状态变量的初始分布，即寿命分布。现有的半随机滤波相关研究中，普遍缺乏对寿命分布进行估计的理论依据，没有充分利用设备退化先验知识。在随后对轴承等的研究[11]当中，采用了数据拟合的方法对寿命分布进行估计；随后，文献[12]在对风电机组齿轮箱的剩余寿命预测中运用核密度估计的方法提高了寿命分布的拟合精度，但该方法计算量较大且只能数值求解。

可以看出，基于随机退化过程建模的方法与半随机滤波方法互有优势，若能结合两类方法的优势，将有望提高对设备剩余寿命的预测精度。为此，本文提出了一种考虑设备退化先验知识的基于半随机滤波的线性随机退化设备剩余寿命预测方法，该方法依据线性随机退化设备的退化失效特点，将描述线性随机退化设备寿命的逆高斯分布作为半随机滤波模型的初始分布，然后利用半随机滤波技术预测设备的剩余寿命。利用历史监测数据和寿命数据通过极大似然方法估计确定模型参数。最后，基于疲劳裂纹增长数据进行了验证和对比，结果表明所提方法能够有效提高剩余寿命预测精度。

1 符号定义与模型假设

为便于描述半随机滤波方法的相关理论，将本文所使用的半随机滤波方法预测模型的符号及其定义描述如下：tk为第k个监测点的时间，称为tk时刻；xk为tk时刻的设备条件剩余寿命；yk为tk时刻获得的设备监测信息；Y1:k为从初始时刻到tk时刻的设备历史监测信息，Y1:k={y1,y2,…,yk}；p0(x0)为设备在t0时刻的剩余寿命概率密度函数，即设备寿命的概率密度函数；p(yk|xk)为tk时刻xk条件下yk的条件概率密度；p(xk|Y1:k)为tk时刻在历史监测信息Y1:k的条件下设备剩余寿命xk的条件概率密度。

根据工程实践中的经验和本文建模的需要，提出以下假设：1)对设备的监测是在离散时间上进行的；2)tk时刻的条件剩余寿命xk是一个随机变量，以概率密度函数描述tk时刻的监测信息yk与xk的关系，其仅与xk有关；3)相邻两次监测期间，不会发生设备维修、替换等操作。

对于假设1)，对设备健康状态的监测是在离散时间上进行的，该假设与监测设备以及工程实际有关，也是工程实际中普遍的情况;对于假设2)，条件剩余寿命的随机性和监测信息与条件剩余寿命之间的随机关系是符合先验知识的，只有存在随机关系才能通过监测数据预测设备的剩余寿命;对于假设3)，设备维修和备件替换会使得当前时刻为止的历史信息与替换维修后的设备无相关性，因此假定为无维修替换。综上所述，本文的假设是合理有依据的，并且将在后续的模型建立中得到使用。

2 半随机滤波模型的建立

在文献[10]模型中，在tk-1到tk时刻的时间间隔内，假如设备未失效，基于假设相邻监测期间未发生维修，则将相邻时刻的剩余寿命关系描述为

(1)

由此可知，xk的存在性仅依赖于xk-1≥tk-tk-1。将剩余寿命减少量直接描述为监测时间间隔，并将剩余寿命视作状态量，xk和xk-1之间所满足的确定性关系即该方法被称为半随机滤波的原因。

为估计tk时刻的剩余寿命xk，求得p(xk|Y1:k)是本文的核心目的。可将表达条件剩余寿命的概率密度函数p(xk|Y1:k)描述为

(2)

通过式(2)可见，为求得给定到当前时刻tk的历史信息Y1:k的条件下设备剩余寿命xk的概率密度函数，需要p(xk,yk|Y1:k-1)和p(yk|Y1:k-1)的函数。基于假设2)所提的条件，可得

p(xk,yk|Y1:k-1)=p(yk|xk,Y1:k-1)pk(xk|Y1:k-1)=p(yk|xk)pk(xk|Y1:k-1)

(3)

通过积分可推导出

(4)

由此，根据式(1)可得

(5)

将式(3)～(5)代入式(2)可得

(6)

即给定历史信息条件下设备剩余寿命的概率密度函数式，式(1)～(6)构成了基于半随机滤波方法进行设备剩余寿命预测的过程。

依据上述的半随机滤波预测模型，通过初始时刻的寿命分布p0(x0)和所有的历史监测信息Y1:k，可迭代得到当前时刻的条件剩余寿命分布的表达式。

3 模型与数据拟合

在基于半随机滤波方法的设备剩余寿命预测中，需要寿命分布p0(x0)和后验概率p(yk|xk)的分布形式。布朗运动驱动的线性漂移过程被称为维纳(Wiener)过程，该过程因具有良好的数学性质而被广泛应用于线性随机退化设备的可靠性分析和剩余寿命预测领域[1]。工程中存在一类线性退化设备，其退化过程可以用线性Wiener过程描述，那么它达到失效阈值的时间服从逆高斯分布，即寿命分布为逆高斯分布。经过国内外学者的广泛研究，逆高斯分布描述的设备寿命分布已具有很广泛的适用性。传统的半随机滤波方法中，受限于设备先验知识的缺乏，半随机滤波方法预测精度又依赖于初始分布的准确性，因此，选取了拟合性较好的威布尔分布以进行具有一般性的数据寿命分布描述。然而，该方法对于这类具有一定的退化过程先验知识的数据仍使用威布尔分布描述寿命分布，使得寿命分布的描述不够准确，进而影响半随机滤波方法的剩余寿命预测结果精度。

为解决该问题，本文首先解决影响预测结果精度的寿命分布即初始分布的确定问题。在Wiener过程中，设备的寿命分布被描述为服从参数为ω，λ和σ的逆高斯分布，然而，由于现实中存在设备失效阈值往往难以确定的问题，在本文中将设备寿命分布描述为两参数的逆高斯分布，即

(7)

式中：x0为初始时刻设备的剩余寿命，即设备寿命；λ和μ为描述分布的参数，两参数的逆高斯分布描述形式规避了对失效阈值的依赖。

其次，半随机滤波方法所需的后验概率密度p(yk|xk)是获得条件剩余寿命分布的必要条件。由于威布尔分布具有良好的拟合特性，为不失一般性，在本文中将后验概率密度p(yk|xk)描述为两参数的威布尔分布，即

p(yk|xk)=ρη(ρη)η-1exp{-(ρη)η}

(8)

在实际中，退化越严重，设备的剩余寿命越小。因此，设备的退化量和剩余寿命间存在反比关系。为描述这一反比关系，本文中选取ρ=1/(A+Be-Cxk)，使得监测信息和剩余寿命之间满足E(yk)∝(A+Be-Cxk)。

最后，根据以上模型设置与描述，线性随机退化设备tk时刻的条件剩余寿命概率密度函数可以表示为

(9)

4 参数估计

为了实现剩余寿命预测方法，需要根据设备的历史监测数据对寿命分布p0(x0)的参数λ和μ以及后验概率p(yk|xk)中参数A，B，C和η进行估计。为此，本文基于极大似然估计方法分别对这类参数分布进行估计。

4.1 p0(x0)的参数估计

根据设备历史监测数据，利用完整寿命数据tj f和截断寿命数据tl可以依据p0(x0)构建似然函数，本文由于采用逆高斯分布描述p0(x0)，因此似然函数可表示为

(10)

式中：参数n为完整寿命数据的组数；m为截断寿命数据的组数；tj f为第j组数据的失效时间；tl为第i组数据的最后监测时间。然后，通过使式(10)最大化来确定模型参数λ和μ。

4.2 p(yk|xk)的参数估计

对于后验概率密度p(yk|xk)中的参数，可以根据设备的历史监测信息数据构建似然函数，即

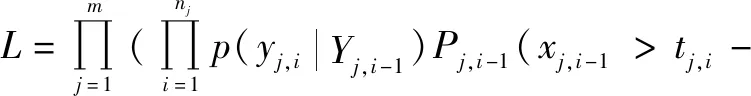
(11)

式中:j为数据组数;nj为第j组数据的监测点个数；假如失效时间存在的话，则tj f表示第j组的失效时间。然后，通过最大化式(11)中的似然函数，可得到A,B,C和η的极大似然估计。

5 实例验证

为验证本文提出的方法，以文献[13]提供的疲劳裂纹数据为依托进行验证研究，该退化数据共有21组，在间隔相同的12个监测时间获取了监测信息，监测时间的单位为百万周期，退化数据的单位为m。选取其中一组数据用于检验剩余寿命预测模型的准确性，其余的数据用于第4章的参数估计。图1所示为疲劳裂纹数据随时间变化的曲线。

图1 疲劳裂纹增长数据Fig.1 Fatigue crack growth data

由图1所示的数据随时间变化的特点可以看出，其退化趋势具有明显的线性规律。因此，若采用线性Wiener过程建模疲劳裂纹数据，对应的寿命分布即为逆高斯分布。因此，采用现有的半随机滤波方法进行剩余寿命预测时，文献[10]模型方法使用威布尔分布拟合寿命分布时就会因为没有充分利用先验知识而导致拟合结果不精确，进而导致预测结果误差较大的问题。为克服这一问题，本文将半随机滤波模型中的初始寿命分布用逆高斯分布描述，使用疲劳裂纹增长数据以验证模型的有效性，并与传统的半随机模型预测结果进行比较。在本文后续的描述当中，将文献[10]模型方法描述为M1，将本文的改进模型方法描述为M2。

5.1 参数估计

为了应用半随机模型，首先估计模型参数。依据先验知识，当疲劳裂纹长度增长到0.040 64 m时就停止了后续监测，认为设备失效。因此，基于这一失效阈值，可以得到数据集中各个设备的失效时间，将其视为设备的寿命数据。具体地，将11组完整寿命数据和9组截断数据代入式(10)，极大化后求得参数的估计值为λ=18.195 9，μ=0.116 3。再对后验概率的参数进行估计，应用式(11)，通过Matlab的多维搜索，即可得出后验概率p(yk|xk)中的参数估计值：A=-0.629 6，B=2.284 1，C=3.636 1，η=24.363 8。

5.2 方法比较

为了验证模型方法(M1)和本文方法(M2)在改进后对寿命分布描述的准确性，将参数估计得到的结果代回两种模型方法中进行对比。图2所示为两种模型方法下设备寿命分布概率密度函数曲线。由于半随机滤波将剩余寿命减少量描述为监测时间间隔，因此依据式(1)可知，检验数据对应的设备寿命为0.12个百万周期。

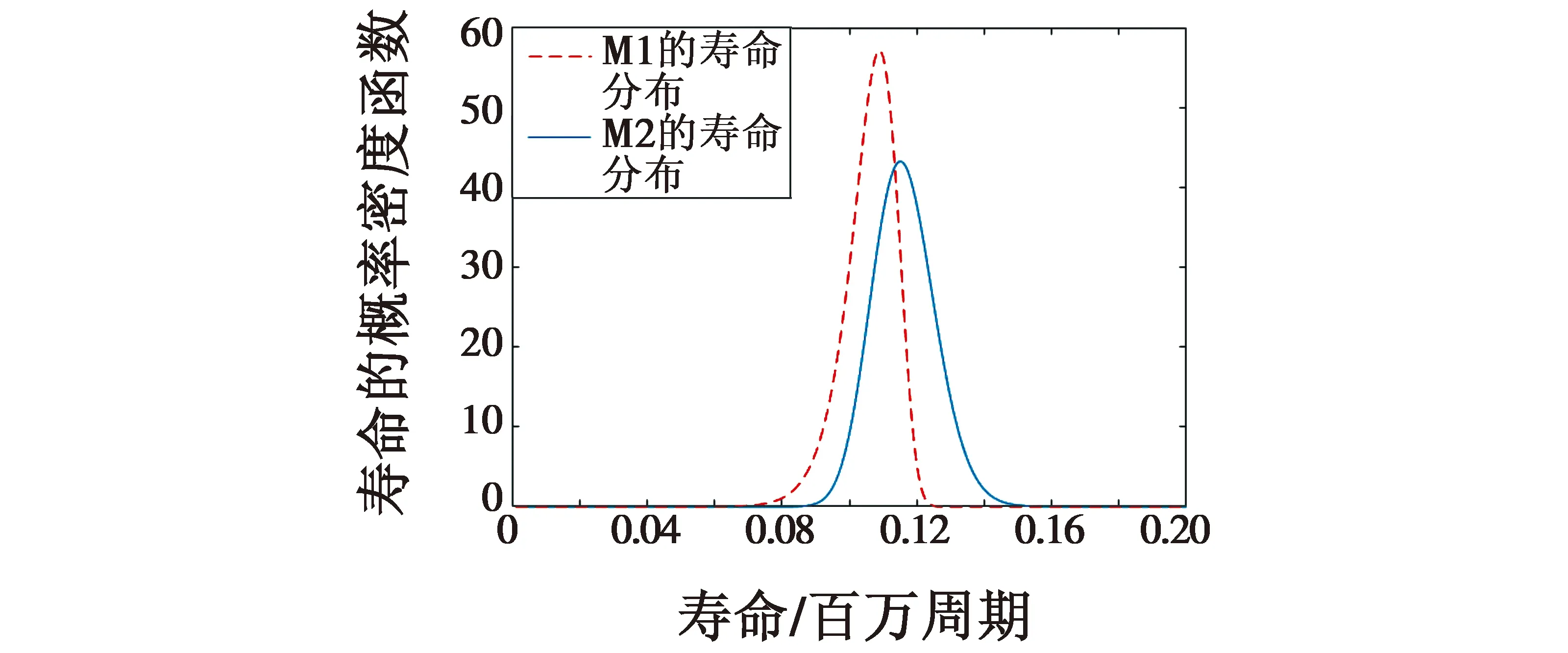
图2 寿命分布概率密度函数Fig.2 PDF of life distribution

由图2可以看出，模型方法(M1)的预测结果在对寿命分布的拟合上是不够准确的，比本文方法(M2)的预测结果要差一些，说明了其精度不足，也体现出了传统模型中寿命分布选择不准确问题。

图3所示为两种模型方法预测的剩余寿命的条件概率密度p(xk|Y1:k)。

图3 剩余寿命的条件概率密度函数Fig.3 PDF of the remaining useful life

由图3可以看出，改进模型方法的概率密度函数方差要小于传统方法，说明本文提出方法的预测不确定性要明显好于传统方法。

图4所示为两种模型方法在各个时刻的剩余寿命预测值的对比。

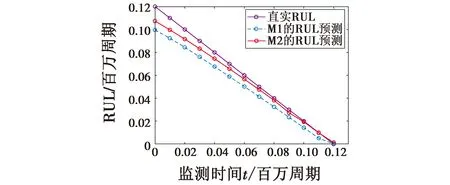
图4 剩余寿命的均值Fig.4 Mean value of the remaining useful life

由图4可知，本文改进方法(M2)的预测结果优于已有的模型方法(M1)，可以看出,改进方法的预测结果与真实值之间更为接近。并且，随着时间推移，新的监测信息对预测结果修正以后，预测值愈发贴近真实值。

图5所示为剩余寿命预测的均方误差(MSE),本文采用MSE描述改进方法和传统方法预测剩余寿命的精度。

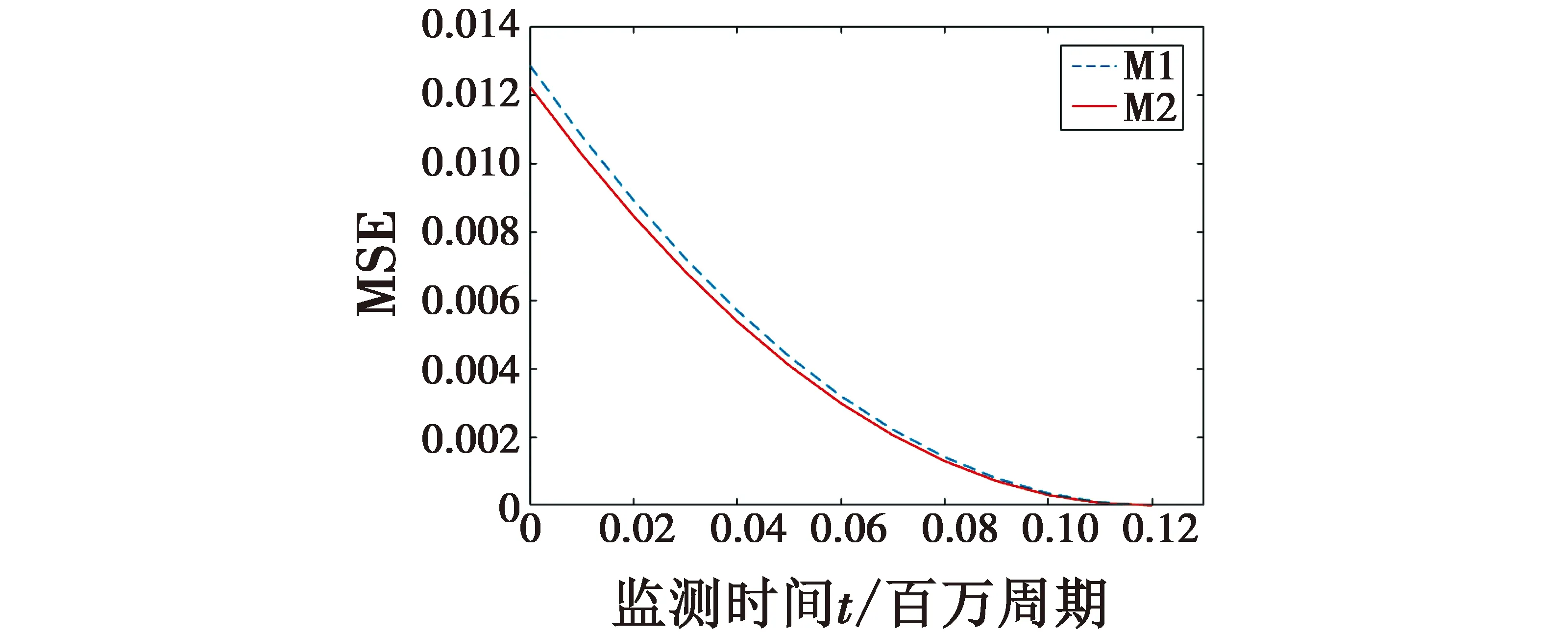
图5 剩余寿命预测的MSEFig.5 MSE of the predicted remaining useful life

由图5可知，本文提出的模型方法(M2)预测误差要小于传统模型方法(M1)。

6 结束语

本文针对工程中随机退化方法中失效阈值难以确定且无法兼顾失效数据和退化数据、半随机滤波方法中初始分布选择缺乏理论依据等问题，在文献[10]预测模型的基础上对其进行改进，将描述线性随机退化设备寿命的逆高斯分布作为半随机滤波模型的初始分布，然后利用半随机滤波技术预测设备的剩余寿命，并给出了模型参数的极大似然估计方法，最后，基于疲劳裂纹增长数据对本文提出的方法进行了验证。结果表明：相比于文献[10]的半随机预测模型，本文所提方法能够更有效地提高剩余寿命预测精度。