基于正六面体测量阵列的磁性目标定位方法

迟 铖，于振涛，王 丹，陶荣华，吕俊伟

(1.海军潜艇学院遥感所，山东 青岛 266000；2.海军航空大学，山东 烟台 264000)

0 引言

近几年，磁梯度张量探测[1-3]作为一种新兴的磁性目标探测技术而受到广泛的关注，其在矿藏资源的勘探、潜艇及未爆弹 (Unexploded Ordnance，UXO)的定位等领域都有重要的应用价值。与传统的磁场总场及矢量场探测相比，磁梯度张量探测具有可以消除地磁背景场干扰的优点，实现对磁性目标的高精度定位。

早在1975年，WYNN[4]就提出了利用磁梯度张量测量信息对目标定位的方法，但是该方法反演得到关于目标位置的4个解，存在单测量点无法确定唯一解的问题，因此需要借助其他信息去除虚假解[5]。2006年，TAKAAKI等[6]提出了利用磁梯度张量和磁场矢量信息的磁性目标单点线性反演定位算法，该定位算法可以实现对目标的单点实时定位，但是该定位算法利用了磁场矢量的测量信息，不可避免地会受到地磁场的估计误差的影响，进而对定位结果带来较大误差;张朝阳等[7]采用平面磁梯度张量系统对单点线性反演定位算法进行了仿真验证;与此同时，利用磁梯度张量测量信息对目标进行定位的非线性优化算法[8-10]也得到了研究，但是存在算法的收敛效率较低以及无法实时定位的问题。

针对目前基于磁梯度张量的单点线性反演定位算法中受地磁场的估计误差影响较大的问题，本文对单点线性反演定位算法进行改进，提出了一种基于正六面体测量阵列的磁性目标定位方法，该方法通过对磁场矢量项做差来消除地磁场估计误差的影响，仿真实验验证了该方法的有效性，并分析得出了磁力仪的精度、系统基线的长度和系统误差参数的校正精度是影响定位精度主要因素的结论。

1 基于磁梯度张量的单点定位方法

1.1 磁梯度张量

当探测系统离磁性目标的距离较远时，可将磁性目标简化为磁偶极子，磁矩为m的磁偶极子在距离r处产生的磁场可以表示为

(1)

式中，μ为真空磁导率，其值为4π×10-7Tm/A。

磁梯度张量是磁场三分量在空间3个方向的变化率，共有9个分量，表达式为

(2)

式中，磁梯度张量的各个分量的表达式为

(3)

式中:下标i,j可分别取笛卡尔坐标系下x,y,z这3个分量中任一个，当i=j时，δi j=1，当i≠j时，δi j=0。由式(3)可得磁梯度张量G具有对称性，且主对角线上的3个分量和为零，因此,9个分量中只有5个是独立的。

1.2 单点线性反演定位算法

TAKAAKI通过对式(1)中的磁偶极子模型推导得到磁场矢量、磁梯度张量和距离矢量之间存在如下关系

(4)

由式(4)可得出磁性目标到测量点的距离矢量表示为

(5)

由式(5)可得，利用单个测量点的磁梯度张量和磁场矢量信息可以直接求得磁性目标的位置坐标，但是式(5)中利用了磁场矢量信息，在实际的磁性目标探测中，磁力仪的测量值是目标磁场和地磁场的矢量合成，因此，需要通过估计地磁场三分量的大小来得到目标的磁场矢量，目标磁场的大小一般为几十nT，而地磁总场的大小在30 000～70 000 nT之间，较小的估计误差就会给目标的定位带来较大的误差。

2 改进方法

由于单点线性反演定位算法中对磁性目标位置坐标的求解利用了磁场矢量，不可避免地会受到地磁场估计误差的干扰，影响定位精度，而地磁场的梯度相对较小，一般小于0.02 nT/m，本文利用地磁场梯度较小的特性，通过正六面体测量阵列上、下两个平面中心点处磁场矢量的差值和磁梯度张量测量信息来计算目标的位置坐标，从而消除地磁场估计误差的影响，具体的计算过程如下所述。

2.1 正六面体测量阵列

本文采用正六面体测量阵列对目标进行定位，正六面体测量阵列[11-13]已被应用于手持式定位，该测量系统由8个磁通门磁力仪组成，可以同时测量正六面体6个平面中心点处的磁梯度张量信息，具体结构如图1所示。

图1 正六面体测量阵列结构图Fig.1 Structure diagram of cube measurement array

由图1可得，以正六面体中心点为坐标原点建立直角坐标系，在正六面体8个顶点位置处分别布控8个磁通门磁力仪(标号为1～8)，磁力仪的坐标系与测量系统坐标系保持一致。测量系统的基线长度定义为相邻2个磁通门磁力仪之间的距离，即正六面体的边长d。

设磁通门磁力仪的测量值为T，表达式为

T=Be+B

(6)

式中:Be为地磁场;B为磁性目标产生的磁场。

通过对磁力仪的测量值进行差分可以近似求得正六面体6个平面中心点处的磁梯度张量，以z轴对应的上、下平面中心点处的磁梯度张量G+和G-为例，表达式分别为

(7)

(8)

式中:Tx1代表编号为1的磁力仪的x分量测量值;⊗代表的分量可由磁梯度张量自身的对称性求得。z轴对应的上、下平面中心点处的磁场值T+和T-分别采用对应平面上4个磁力仪的测量值的平均，表达式分别为

(9)

(10)

式中，T1代表编号为1的磁力仪测量的磁场值。

2.2 基于正六面体测量阵列的目标定位原理

由式(4)可得，利用正六面体测量阵列z轴对应的上、下平面中心点处的磁梯度张量测量信息G+和G-，建立关于目标位置的方程组为

(11)

式中，B+和B-分别为磁性目标在正六面体测量阵列z轴对应的上、下平面中心点处产生的磁场值，磁性目标与测量点间的分布如图2所示。

图2 磁性目标与测量点间的分布示意图Fig.2 Distribution between a magnetic target and the measurement point

由图2可得

(12)

将式(12)代入式(11)，可得

(13)

通过对式(13)中的两个方程做差可得

(14)

由于地磁场的梯度一般小于0.02 nT/m，因此当d*较小时(一般小于1 m)，可以认为图1中z轴对应的上、下平面中心点处的地磁场Be+和Be-近似相等，于是有

T+-T-=Be+-Be-+B+-B-≈B+-B-

(15)

则式(14)可变为

(16)

由上式可求得

(17)

则由式(17)可以直接求得磁性目标的位置，实现对磁性目标的单点实时定位。改进方法利用磁场矢量的差值及磁梯度张量的测量信息进行定位，不需要估计地磁场的大小，且地磁场的梯度很小，对改进定位方法中目标位置计算的影响也很小，因此，改进定位方法可以消除地磁场的干扰。

3 仿真实验

本文设计仿真实验对改进方法的定位效果进行验证，初始仿真条件设定如下：采用如图1所示的坐标系，磁力仪精度为0.01 nT，系统基线长度为0.5 m，假设磁性目标由点(10 m,10 m,10 m)位置处沿着向量(1,1,1)的方向向外移动，磁性目标的磁矩为(5 000 000 Am2,200 000 Am2,200 000 Am2)，测量区域的地磁场为(29 339 nT,2741 nT,42 323 nT)，地磁场测量的相对误差为0.5%。

仿真流程如下：首先根据磁偶极子模型，仿真计算磁性目标在8个磁力仪位置处产生的磁场值，叠加地磁场之后便是磁力仪的测量值，通过式(7)和式(8)计算z轴对应的上、下平面中心点处的磁梯度张量值，同时根据式(9)和式(10)计算z轴对应的上、下平面中心点处的磁场值；代入式(17)计算得到磁性目标的位置坐标。

图3所示为初始仿真条件下现有定位方法与本文提出的改进定位方法在不同探测距离处对磁性目标的定位结果对比。

图3 现有方法与改进方法定位结果对比图Fig.3 Localization results of the original method and the proposed method

由图3可得，本文所提改进方法的定位效果优于现有方法，随着定位距离的增加，现有方法的定位误差不断增大，当磁性目标距离测量系统86.6 m时定位误差大于30 m，而改进方法的定位误差一直较小，当目标距离测量系统86.6 m时定位误差在5 m以内。

分析影响改进方法定位误差的因素可能有：1)磁力仪的精度；2)正六面体测量系统基线的长度；3)正六面体测量系统误差参数的校正精度。

1)不同磁力仪精度下改进方法的定位误差。

首先仿真分析当测量系统中磁力仪的精度分别为0.1 nT，0.01 nT，0.001 nT时，利用改进方法进行定位的误差结果，如图4所示。

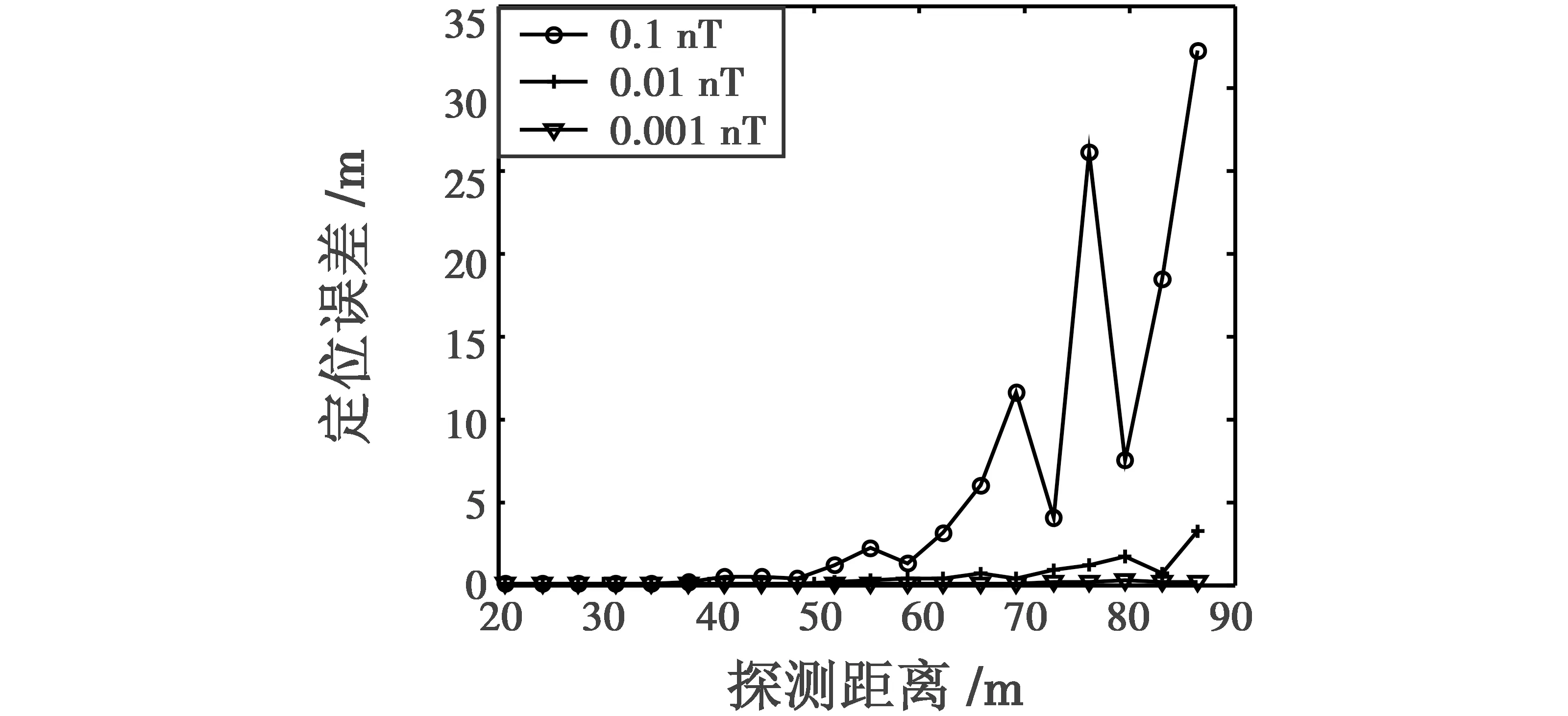
图4 不同磁力仪精度下定位误差随探测距离的变化Fig.4 Variation of locating error with detection range under different magnetometer precisions

由图4可得，当磁性目标距离测量系统较近时，磁力仪精度为0.1 nT与0.001 nT的定位误差都较小，定位误差小于1 m，随着探测距离的增加，不同磁力仪精度的定位误差都增加，对于远距离目标，磁力仪精度为0.1 nT的定位误差较大，当距离为86.6 m时的定位误差为32.3 m，当磁力仪精度为0.001 nT时，对远距离目标的定位误差较小，对距离86.6 m目标的定位误差仅为0.2 m。

2)不同基线长度下改进方法的定位误差。

仿真分析当正六面体测量系统的基线分别为0.3 m,0.5 m,0.8 m时，不同的探测距离下改进方法对磁性目标的定位误差结果,如图5所示。

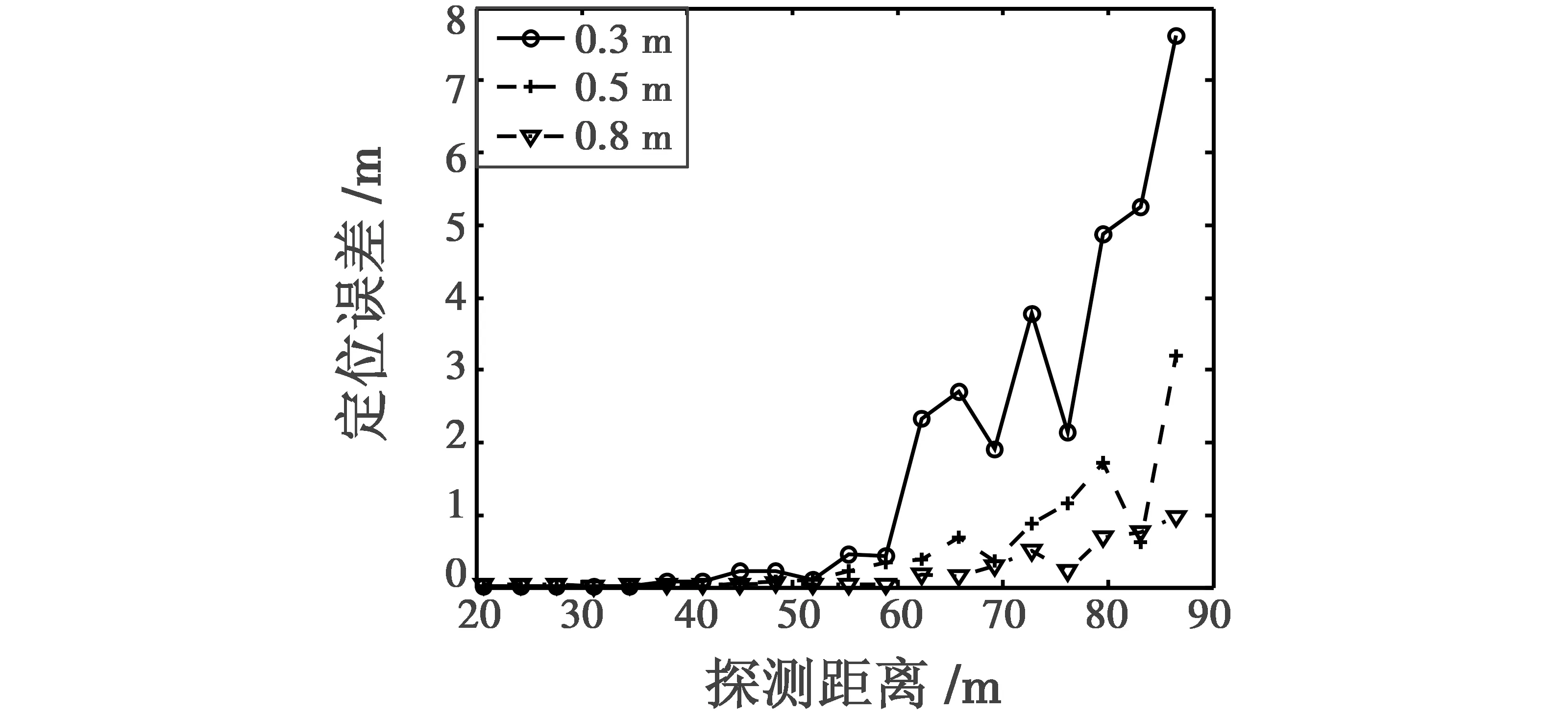
图5 不同基线长度下定位误差随探测距离的变化Fig.5 Variation of locating error with detection range under different baseline distance

由图5可得，对于近距离目标，不同基线长度的定位误差都较小(1 m以内)，随着探测距离的增加，不同基线长度的定位误差也在增加，当探测距离一定时，定位误差随着基线长度的增大而减小。

3)系统误差参数校正精度对定位误差的影响。

正六面体测量阵列中单个磁力仪存在三轴非正交、灵敏度不一致、零点偏置等误差，同时磁力仪之间也存在不对正误差[14]，上述误差均会对定位结果产生影响，文献[14]提出一种基于线性误差模型的校正方法，但是该方法对误差模型进行简化，导致校正精度不高。

仿真分析,当存在系统误差时、利用文献[14]的线性误差模型对系统误差进行校正后以及理想无系统误差的情况下，正六面体测量系统对磁性目标的定位误差结果,如图6所示。

图6 不同系统误差条件下定位误差随探测距离的变化Fig.6 Variation of locating error with detection range under different system errors

由图6可得:当存在系统误差时，定位误差很大，直接导致定位结果不能使用，因此,在定位前应首先对测量系统的误差进行校正；当使用文献[14]的线性化误差校正方法校正后，定位误差略有减小，但是远大于理想无误差情况，定位误差随着探测距离的增加而增大，当探测距离为86.6 m时,定位误差为67.98 m，因此,可以得出，线性化误差校正方法对系统误差的校正精度不高，导致定位误差较大。

4 结论

本文通过对单点线性反演定位算法进行改进，提出了一种基于正六面体测量阵列的磁性目标定位方法，该方法可以克服目前单点线性反演定位算法中受地磁场干扰影响较大的问题。通过仿真实验分析可得，改进方法对磁性目标的定位效果较好，定位误差明显小于现有方法。改进方法对磁性目标定位精度的主要影响因素有磁力仪的精度、系统基线的长度和系统误差参数校正精度，因此,在实际的磁性目标定位时，可以通过提高磁力仪的精度、增加系统基线的长度和提高系统误差参数校正精度来减小磁性目标的定位误差，基于正六面体测量阵列的磁性目标定位方法可以加载于运动载体平台上实现对磁性目标的单点实时定位，不足之处在于，正六面体测量阵列需要校正的误差参数较多，在下一步的工作中应该研究正六面体测量阵列的误差校正方法。