基于非均匀采样系统的无模型自适应控制

叶金鑫，谢丽蓉，王宏伟

(1.新疆大学，乌鲁木齐 830000;2.大连理工大学,辽宁 大连 116000)

0 引言

随着现代工业的飞速发展，非线性系统也变得越来越复杂，然而由于不同条件的限制，系统采用不同的频率进行工作，因而形成了多率采样数据系统(简称多率系统)，因此想要建立系统精确的数学模型，并对其模型进行控制相当困难[1]。

在输入非均匀刷新和输出周期采样系统中，许多学者进行了系统辨识[1-3]和控制[4-9]方面的研究，虽然在非均匀系统控制方面取得了很多成果，但大多数仍集中在线性系统上。近年来，对于非均匀采样的非线性系统辨识[10-13]已经获得许多研究成果，但是对于非线性系统的控制方法却并不多。在现实生活中，大多数系统具备非线性、大时滞强耦合特性，且存在建模困难、难以设计高精度的控制器等问题。侯忠生等[14-15]针对这类系统问题，提出了一类无模型自适应控制，该方法的特点是：一种通过线性化设计的控制器，在离散非线性系统的等效数据点上使用了一种新的动态方法，该方法设计简单，易于实现。在设计控制器时，不需知道系统的确切模型，只需知道系统的输入和输出数据即可。对于非线性系统的无模型自适应控制有很多研究成果，包括无模型自适应鲁棒控制[16-17]、无模型自适应积分终端滑模控制[18]、自适应积分滑模控制[19-20]、无模型自适应预测控制[21-22]、无模型自适应滑模矢量控制[23-24]、无模型自适应迭代控制[25]及无模型参数迭代寻优控制[26-27]。但对于非均匀采样非线性系统，文献[28]提出了一种利用支持向量回归建模，设计了预测控制算法；文献[29]利用在当前输入输出数据平衡点处建立线性化数据模型，在投影算法计算下，对伪雅可比矩阵(Pseudo Jacobian Matrix，PJM)在线实时估计，设计出了无模型自适应控制器，并取得了很好的控制效果；文献[30]对非均匀采样系统利用余弦项展开，提出了一种采用非线性模型预测控制，取得了较好的效果。综上所述，常规的非均匀采样非线性离散系统的无模型自适应控制中存在着两个问题：其一，未考虑输出采集数据受扰动误差带来的影响，所设计的控制器控制精度会受到影响；其二，惩罚因子主要根据经验来选择，并且不能自动将其调整为最佳值，惩罚因子会影响系统的收敛速度、超调量等整体系统的性能。

本文主要创新点为：采用跟踪-微分器[31-32]对输出数据进行滤波，利用输入数据和输出滤波数据在等价动态平衡点处建立动态化模型，并设计一种新的无模型自适应控制器；利用最速下降法对控制律和PJM估计公式中的惩罚系数迭代优化，并对该控制方法稳定性进行分析。

1 非均匀采样系统问题的描述

1.1 非均匀采样非线性模型

考虑如下连续非线性系统[29]

(1)

式中，y(t)∈R1,u*(t)∈R1,x(t)∈Rn,Γ(·)分别为系统输出、输入、状态向量和非线性函数，R表示实数集。式(1)中的系统输入信号u*(t)满足

(2)

(3)

采用提升技术，提升变量构造如下

(4)

此时，可将系统式(3)转换成如下离散系统，即

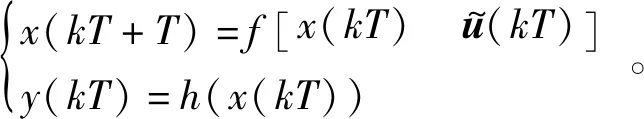
(5)

1.2 线性模型与非线性模型的关系

设连续过程的线性状态空间模型为

(6)

式中，Ac,Bc,C为适当维数的矩阵,Ac∈Rn×n,Bc∈Rn×p。

由1.1节可知，非均匀采样输入数据和均匀采样输出数据分别为u*(kT+ti)，y(kT)，并且i=1,2,…,p-1。所以对一个帧周期T内离散化系统式(6)，即

(7)

将式(6)～(7)整理得到如下离散状态空间模型

(8)

(9)

令In是n阶单位矩阵，系统式(8)可等价为

(10)

也可表示为一般形式

(11)

式中，

{

a(z-1)=z-ndet[zIn-Α]=1+a1z-1+a2z-2+…+anz-n

b0(z-1)=b00z0+b01z-1+b02z-2+…+b0nz-n

⋮

bi(z-1)=bi1z-1+bi2z-2+…+binz-n,

i=1,2,…,n。

在文献[29]中，非线性系统式(5)与线性系统式(8)的关系是：非线性系统Sp可以看作是在多个工作点的局部线性模型式(11)经过非线性加权组合得到，即

(12)

式中，φ(kT)=[y(kT-T),…,y(kT-nT),u*(kT-T),…,u*(kT-nT),u*(kT+t1-T),…，u*(kT+t1-nT),u*(kT+tp-1-T),…,u*(kT+tp-1-nT)]T。

模型式(12)是fl[φ(kT)]在第l个非线性加权函数和gl[φ(kT)]在第l个工作点处的局部线性函数。因此模型式(12)进一步表示为

y(kT)=f(φ(kT))。

(13)

2 改进的无模型自适应控制

可将系统式(13)看作是多输入单输出(MISO)系统，表示为

y(kT+T)=f(y(kT),…,y(kT-nyT),u(kT),…,u(kT-nuT))

(14)

式中:

(15)

假设 1[14-15]函数f(·)是关于系统控制输入信号u(kT)的偏导数,是连续的。

假设 2[14-15]非线性函数式(14)满足广义Lipschitz条件，即对于任意时刻k1≠k2，k1≥0,k2≥0和u(k1T)≠u(k2T)，均有

||
y(k1T+T)-y(k2T+T)||
≤a||
u(k1T)-u(k2T)||

(16)

式中:y(kiT+T)=f(y(kiT),…,y(kiT-nyT);u(kiT),…,u(kiT-nuT)),i=1,2;常数a>0。

定理1[14-15]若非线性系统泛模型式(14)满足假设1和假设2，且对所有时刻kT，有||

Δu(kT)||

=||

u(kT)-

u(kT-T)||≠0，一定存在一个被称为PJM的时变参数Φ(kT)∈Rp×1，使得泛模型系统式(14)等价于如下紧格式动态线性化(CDFL)的一类泛模型

Δy(kT+T)=ΦT(kT)Δu(kT)

(17)

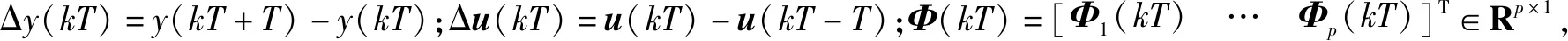
Φ(kT)||

≤b，常数b>0。

2.1 跟踪-微分器

本文算法中加入跟踪-微分器[31-32]，目的是对非均匀采样非线性系统输出数据y(kT)进行滤波，提高算法对系统的扰动或噪声的抗干扰能力。跟踪-微分器原理是：对于一个跟踪微分系统，给定一个非均匀采样系统的输出信号v(t)，它将会输出产生两个信号x1和x2，其中，x1是v(t)所要的输出跟踪信号，x2是v(t)的近似输出微分信号。

二阶离散的跟踪-微分器公式为

(18)

式中：p为离散化采样步长；h和r分别为滤波因子和速度因子。定义非线性函数f(·)为

{f(x1(kT),x2(kT),v(kT),r,h)=-rsat(g(kT),δ)y(kT)=x1(kT)-v(kT)+hx2(kT)δ=hr,δ1=hδ

(19)

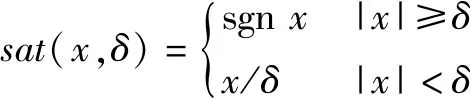
(20)

(21)

2.2 无模型自适应控制器设计

考虑如下控制准则函数

(22)

式中，惩罚因子λ>0，用于调节输入量过大的变化。将式(17)代入准则函数，并对其极小化，即

(u(kT)-u(kT-T)))+2λ(u(kT)-u(kT-T))=0

(23)

求得控制器

u(kT)=u(kT-T)+(λI+Φ(kT)ΦT(kT))-1·

Φ(kT)(y*(kT+T)-y(kT))

(24)

式中，I为单位矩阵。

由于每次实施控制算法计算时，矩阵都要求逆运算，当系统输入信号的维数很大时，求逆非常耗时间，不利于现实中的运用,因此对控制算法进行简化，得到不含求逆的改进控制算法

(25)

式中，步长因子ρ∈(0,1]，它的加入使算法更具灵活性，且将在稳定性和收敛性分析中用到。

对于一般系统来说，即使是简单的线性系统，伪偏导数Φ(kT)一般也是未知的、时变的。因此，为实施控制算法式(25)，采用如下性能指标在线估计伪偏导数Φ(kT)的值

(26)

式中，惩罚因子μ>0，它的加入是为了限制PJM的估计值产生过大的变化。

对准则函数进行求偏导，令其导数等于零，得

(27)

由于PJM辨识算法需要求逆运算，当系统输入维数很大时，求逆是非常麻烦的，不利于实际运用，因此对辨识算法进行简化得

。

(28)

2.3 对惩罚因子进行改进

惩罚因子λ和μ具有两个主要功能：1)限制控制量和PJM输入变化，这些变化会影响系统响应速度和超调量，同时减少系统稳态误差并确保控制输入信号的平滑性；2)防止式(25)和式(28)出现分母为零的特殊情况，选择合适的λ和μ值可确保系统稳定性，并在闭环系统中优化响应速度和超调量之间的平衡。现有方法主要根据经验来选择λ和μ，并且不能自动将其调整为最佳值。本文采用最速下降法进行优化，提出了惩罚因子在线迭代自适应的改进方法，迭代寻找能使控制律和伪偏导数达到最优的惩罚因子值。

1)对控制律中的惩罚因子改进。

对式(25)的惩罚因子做迭代改进，即

λ(kT+T)=λ(kT)-β1▽J(u(kT))

(29)

式中,β1为学习率。

(30)

2)对PJM中的惩罚因子改进。

对式(28)的惩罚因子做迭代改进，即

(31)

式中,β2为学习率。

(32)

因此就有PJM辨识算法

(33)

对于式(33)引入如下参数重置机制

(34)

Δu(kT-T)||

式中，ε是一个充分小的正数。参数重置机制的引入是为了使PJM辨识算法具有更强大的功能来跟踪时变参数。

得到控制器算法为

(35)

最后，将整个改进无模型自适应控制算法总结如下：

1)设置系统输入、输出初值和PJM初值，以及参数η∈(0,2]，μ(1)>0，ρ∈(0,1]，λ(1)>0;

2)采集非均匀采样非线性系统当前实际输出y(kT)和期望输出yr(kT+T);

3)设置参数离散化采样步长p、滤波因子h、速度因子r,由式(18)～(21)得到输出数据y(kT)的跟踪数据x1(kT);

5)利用式(35)计算并实施u(kT)；

6)设置参数学习率β1,β2，根据式(29)和式(31)分别对λ(kT),μ(kT)进行迭代更新;

7)返回2)，k=k+1，继续循环。

3 性能分析

为了分析所得新设计的MFAC闭环系统收敛性，做如下引理。

限于篇幅，证明略。

引理2定义

(36)

限于篇幅，证明略。

定理2对于非均匀采样非线性系统(14)，在假设1和假设2满足的条件下，MFAC方案式(33)～(35)具有如下性质：当y*(kT+T)=y*，为常数时，存在一个正数λmin>0，使得当λ*(kT)>λmin时有：

2)闭环系统是BIBO稳定收敛的，即输出序列{y(kT)}和输入序列{u(kT)}是有界的。

限于篇幅，证明略。

4 仿真实例

4.1 仿真1

考虑如下非均匀非线性非仿射离散系统

y(kT+T)=[y(kT)y(kT-T)y(kT-2T)·
(u*(kT+t1-T)(y(kT)-1)+u*(kT))]/
[1+y2(kT)+y2(kT-T)+y2(kT-2T)]

(37)

该非均匀采样非线性系统的采样方案为：帧周期T=1 s，p=2，t1=0.4 s，被控系统的参数、阶数都是时变的。

期望输出信号yr(kT+T)=0.5×(-1)round(kT/50)。

为了验证本文控制方法的优越性，使用本文控制方法与MFAC方法分别对输入刷新和输出周期采样非线性系统的控制仿真图进行比较。MFAC方法的惩罚因子选取为λ=1，μ=1；本文控制方法的惩罚因子λ(1)=1,μ(1)=1，步长因子选为β1=0.01，β2=0.5，仿真结果见图1-图3。

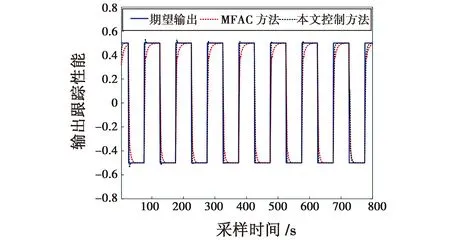
图1 非均匀采样系统的跟踪曲线对比图(仿真1)Fig.1 Comparison of tracking curves of non-uniform sampling system(Simulation 1)

图2 控制输入曲线对比图(仿真1)Fig.2 Comparison of control input curves(Simulation 1)

图3 绝对值误差曲线对比图(仿真1)Fig.3 Comparison of absolute value error curves(Simulation 1)

由图1可知，本文提出的控制方法明显优于MFAC方法，该方法虽然有超调量，但是超调过后能够很好地贴近跟踪曲线，收敛速度快。由图2可知，本文的控制输入量波动小。

此外,通过绝对值误差曲线对本文所设计的控制方法与MFAC方法进行仿真以及性能对比。平均绝对值误差为

(38)

均方根误差为

(39)

由图3可知，本文控制方法的绝对值误差明显小于MFAC方法的绝对值误差。

表1所示为仿真1中2种方法性能指标比较。

表1 2种方法性能指标比较(仿真1)Table 1 Comparison of performance indexes of two methods(Simulation 1)

由表1可知，性能指标明显增大，综合而言，本文控制方法具有更优的控制性能。

4.2 仿真2

为了进一步说明本文方法的有效性，采用非均匀非线性非仿射离散系统[29]，即

(40)

期望输出信号

(41)

该非均匀采样非线性系统是由两个子系统组成，采样方案为：帧周期T=1 s，p=2，t1=0.6 s，被控系统的参数、阶数都是时变的。

文献[29]控制方法的惩罚因子选取为λ=0.6,μ=0.5，本文控制方法的惩罚因子选取为λ(1)=0.6,μ(1)=0.5，步长因子选取为β1=0.05，β2=0.1，仿真结果见图4-图6。

图4 非均匀采样系统的跟踪曲线对比图(仿真2)Fig.4 Comparison of tracking curves of non-uniform sampling system(Simulation 2)

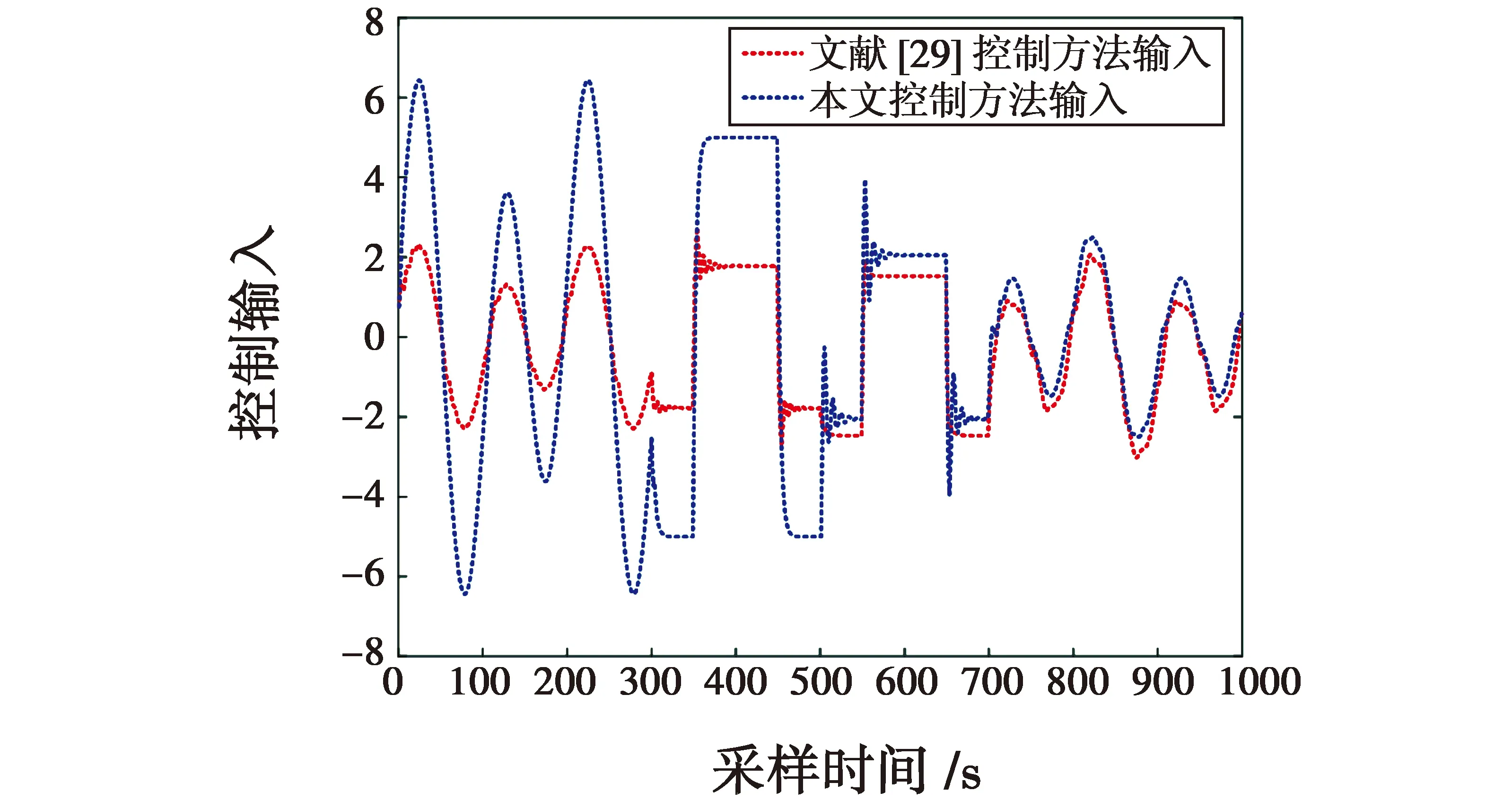
图5 控制输入曲线对比图(仿真2)Fig.5 Comparison of control input curves(Simulation 2)

图6 绝对值误差曲线对比图(仿真2)Fig.6 Comparison of absolute value error curves(Simulation 2)

通过与文献[29]仿真对比，由图4可知，本文控制方法跟踪曲线超调量小、波动小，能够很好地贴近曲线。由图5可知，本文控制输入曲线波动大，但能够很好地跟踪系统输出。由图6可知，本文控制方法的绝对值误差小于文献[29]控制方法的绝对值误差。

表2所示为仿真2中2种方法性能指标比较。

表2 2种方法性能指标比较(仿真2)Table 2 Comparison of performance indexes of two methods(Simulation 2)

由表2可知，无论是平均绝对值误差还是均方根误差，本文控制方法都比文献[29]控制方法要小，因此，本文控制方法具有更好的控制性能。

5 结论

对于非均匀采样离散时间非线性系统，本文提出一种新的无模型自适应控制方法。该方法利用跟踪-微分器对系统的输出数据进行滤波，设计无模型自适应控制器，并且使用最速下降法对控制律和PJM估计中的惩罚系数进行迭代优化。仿真结果表明：实际曲线能够很好地贴近期望曲线，减少扰动误差带来的影响，控制精度高，说明了本文所设计控制方法的可行性和有效性。对于输入非均匀周期刷新和输出非均匀周期采样非线性系统，下一步工作对其进行探讨和研究。