基于全极化信息融合的海杂波中漂浮小目标检测算法

夏 鄂，尹鹏智

(中南大学自动化学院，长沙 410000)

0 引言

海杂波特性研究对于海面监视雷达研究而言是一个极重要的难点[1]，雷达目标检测的性能会受到海况、目标尺寸以及雷达的擦地角等参数的影响。实际雷达回波中的海杂波信号常常会淹没目标回波信号，海面环境恶劣多变，雷达检测性能通常会受到海况的影响。科研人员在近60年的研究过程中，深入开展了海杂波的特征[2]的研究，基于这些特征提出的众多目标检测算法均可看作单一特征检测，但是算法的性能难以尽如人意，在工程应用中有较大的难度[3-4]。

目前主流的检测算法之一是多特征的检测算法，并且研究人员结合不同的检测器算法已经取得了众多成果。SHUI等[5]提出了一种3特征海面小目标检测算法；LI等[6]提出了基于SVM模型的虚警率可控的检测算法；GU等[7-8]在传统PCA降维算法基础上提出了基于PCA异常检测器。以上算法均是在单一极化模式下讨论算法检测性能，但是在实际应用中，只能选取一种极化的雷达信息进行目标检测，而一种算法在不同极化模式下的雷达目标检测性能不尽相同。实际工程中更希望能够利用雷达回波的所有信息，这样更有助于目标检测。本文对此提出了基于全极化信息的6特征融合的检测算法在海杂波中检测目标。

1 检测问题与数据分析

1.1 检测问题分析

海面漂浮小目标的检测问题可被总结为一种二元假设检验，其数学表达式为

(1)

s.t.n=1,2,…,N;J∈{HH,HV,VV,VH};p=1,2,…,P

式中：H0表示无目标的检测单元;H1表示检测单元内存在目标;J表示极化模式，共有 HH，HV，VV，VH 4种；xJ(n),sJ(n),cJ(n)分别表示J极化模式下的接收向量、目标回波和检测单元中的海杂波回波；N为脉冲数目；P为参考单元编号。

1.2 IPIX雷达实测数据描述

本文使用1993年的IPIX实测数据，每个数据集包含14个目标单元(分别组成1个主目标单元以及2～3个次目标单元)，各距离单元有217个脉冲。各数据集包含4种极化(HH，HV，VV，VH)模式下的雷达回波脉冲，取其中10组数据进行算法分析。各数据集的具体信息如表1所示。

表1 数据集描述Table 1 Data set description

2 检测算法设计

2.1 基于全极化信息的特征

海杂波目标检测在时域和多普勒域均取得了较多研究成果，因此，本文从这两个域出发进行特征提取。在时域选取的特征有相对幅度标准差(RSD)、相对平均振幅(RAA)以及相对平均功率(RAP)。在多普勒域选取的则是相对多普勒向量熵(RVE)、相对多普勒峰高(RPH)[9]以及相对多普勒谱峭度(RDK)。下文将详细介绍特征定义，以及基于全极化信息的6特征基于全极化信息的相对平均振幅(PRAA)、基于全极化信息的相对平均功率(PRAP)、基于全极化信息的相对幅度标准差(PRSD)、基于全极化信息的相对多普勒向量熵(PRVE)、基于全极化信息的相对多普勒峰高(PRPH)、基于全极化信息的相对多普勒谱峭度(PRDK)提取算法[10-11]。

2.2 基于全极化信息的时域3特征

2.2.1 基于全极化信息的相对幅度标准差(PRSD)

受海浪周期性起伏的影响，海杂波幅度出现周期性变化，目标单元回波幅度的起伏要大于杂波单元，因此可以通过信号幅度标准差区分杂波与目标。在设计假设检测量时，参考似然比函数的设计思想，将二元假设的两个检测量相除来消去单位，此时检测量变为相对值，即检测门限变成了无量纲相对值。定义待检测单元的回波幅度标准差与参考距离单元的回波幅度标准差的比值为RSD,即

(2)

式中：std(·)表示求标准差；xJ和xp,J分别为待测单元与参考杂波单元的回波幅度。

将4种极化模式的相对幅度标准差做几何平均即可得到PRSD，即

2.2.2 基于全极化信息的相对平均振幅(PRAA)

幅度特征作为一种最直接的特征表现，可以从能量角度来分辨目标单元与杂波单元。带有目标信息的信号能量通常强于该状态下单一海杂波信号，相对平均振幅定义为

(3)

同样的，平均幅度的比值定义为RAA，即

(4)

PRAA是对4种极化模式的相对平均振幅做几何平均后得到，即

(5)

2.2.3 基于全极化信息的相对平均功率(PRAP)

主目标单元的信号平均功率受到目标信号的影响，表现出与纯海杂波单元不同的特性。回波信号的多普勒差异可以通过平均功率来表征，以此判断是否含有目标信息。信号平均功率定义为

(6)

式中：x代表返回时间序列；N为回波信号的长度。同理，RAP为

(7)

PRAP是对4种极化模式的相对平均功率做几何平均后得到，即

(8)

2.3 基于全极化信息的多普勒3特征

J极化模式下的xJ(n)是雷达回波信号，其多普勒谱定义为

(9)

式中：fd为多普勒频率；采样周期Tr=0.001 s。

6号数据的海杂波信号和目标信号的4种极化模式下的多普勒谱分别如图1、图2所示。

图1 海杂波信号在不同极化模式下的多普勒谱Fig.1 Doppler spectrum of pure sea clutter signal under different polarizations

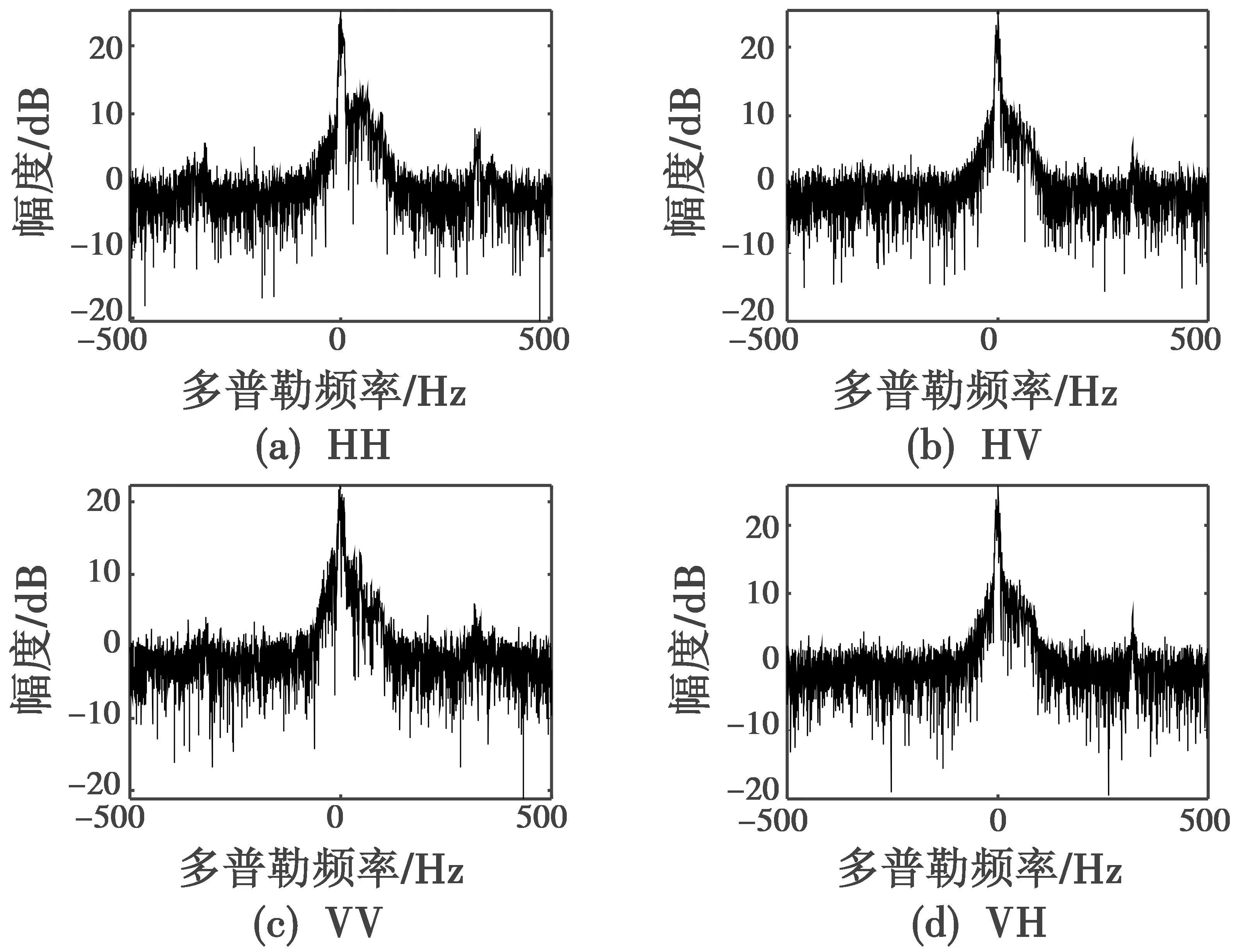
图2 目标信号在不同极化模式下的多普勒谱Fig.2 Doppler spectrum of target signal under different polarizations

不同极化模式下，待检测信号的多普勒谱位置相对固定，但是海杂波的分布与目标信号的分布有明显差异。为提升海杂波与待检测目标的可分性，可以将4种多普勒谱进行融合。对4种极化模式的多普勒谱进行算术平均得到基于全极化信息的多普勒谱定义如下

(10)

海杂波与目标信号在基于全极化信息的多普勒谱中具有明显差异性，如图3所示。

2.3.1 基于全极化信息的多普勒谱向量熵

熵量化了混乱程度，熵越大则表示越混乱。海浪比规则的目标物体让回波信号拥有更大的熵值。对比主目标单元与纯海杂波单元的多普勒谱可以发现，纯海杂波单元的多普勒谱的混乱程度更大。

向量熵是一种特殊的熵，也可用于量化混乱程度。向量熵能够有效衡量向量中元素的波动情况。归一化后的多普勒谱定义为

(11)

式中,X(fd)为回波时间序列经过傅里叶变换后的结果。

归一化后的多普勒谱的向量熵(VE)定义为

(12)

PRVE定义为

(13)

2.3.2 基于全极化信息的多普勒谱峰高度(PRPH)

信号的多普勒谱中，目标信息的存在使得能量更多地聚集于目标的多普勒频率位置，目标单元具有更加尖锐的多普勒谱，PRPH可描述这种特征，其定义为

(14)

式中：fdmax为多普勒谱峰值对应的频率；Δ=[-δ1,-δ2]∪ [δ2,δ1],定义为参考多普勒频率区间,#Δ代表属于集合Δ的元素数量，IPIX数据集的参数取值δ1和δ2分别为50 Hz和5 Hz。

2.3.3 基于全极化信息的多普勒谱峭度(PRDK)

多普勒峭度[12-14]量化了多普勒谱曲线的陡峭程度，其数值计算的定义为多普勒谱的归一化四阶中心矩，多普勒峭度定义为

(15)

式中：Xi(fd)为各个频点全极化多普勒谱幅值;Q为整个多普勒谱的点数。

PRDK定义为

(16)

2.4 基于全极化信息的6全极化特征可分性分析

为了验证6全极化特征的可分性，选择6号数据进行验证，观测时间1.024 s，其10个纯杂波单元与主目标单元的各特征分布直方图如图4所示。如果主目标与纯杂波的直方图出现重叠，即说明该特征无法作为单一的检测量对目标进行有效检测。

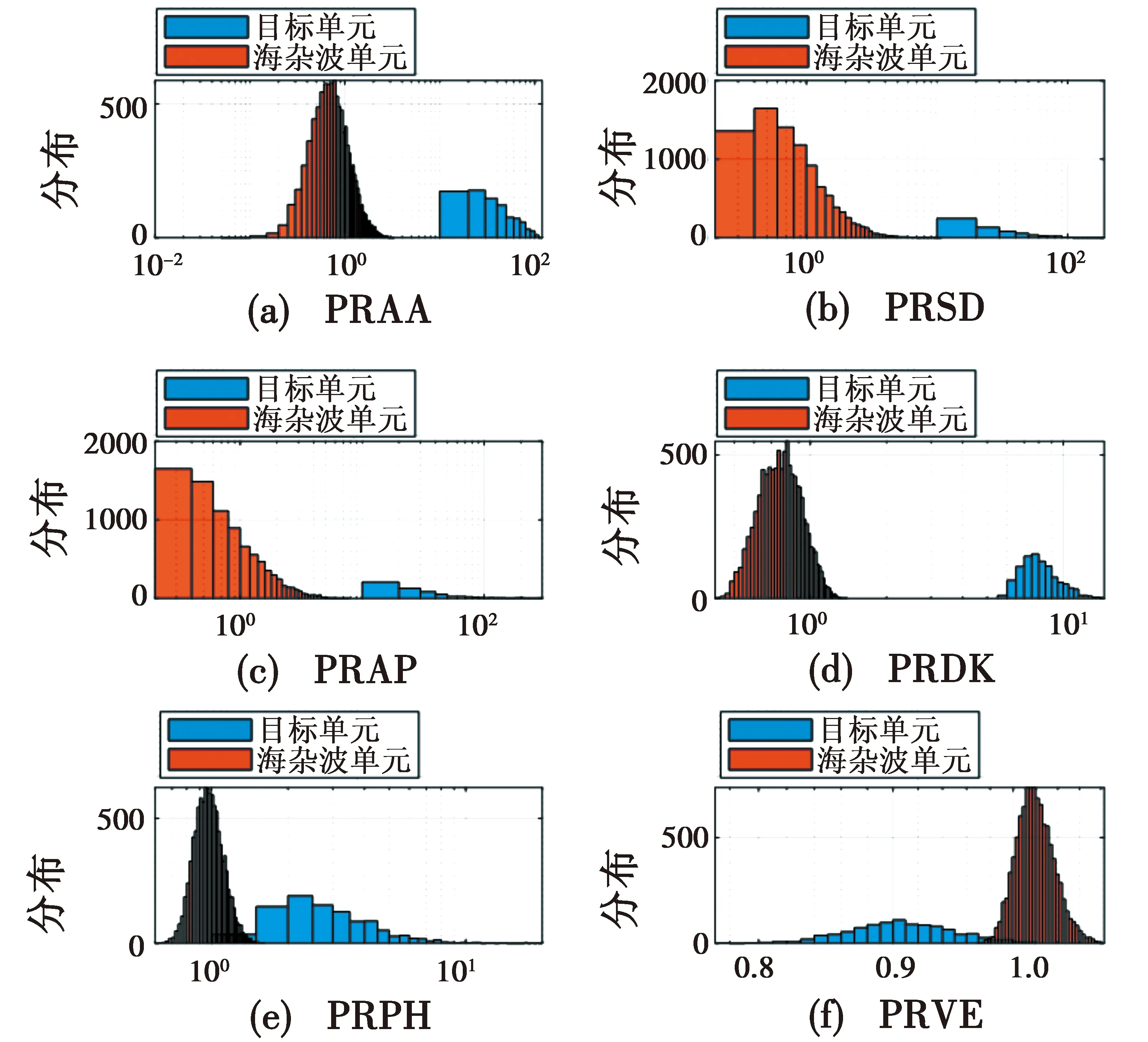
图4 基于全极化信息的特征分布直方图Fig.4 Feature distribution histogram based on full polarization information

图4中的特征PRPH与PRVE并没有完全分离，但是PRAA，PRSD，PRAP和PRDK的分布直方图基本分离，然而并不能确定其是否完全分离。因此，再次做出特征的归一化概率分布图，分布结果如图5所示。

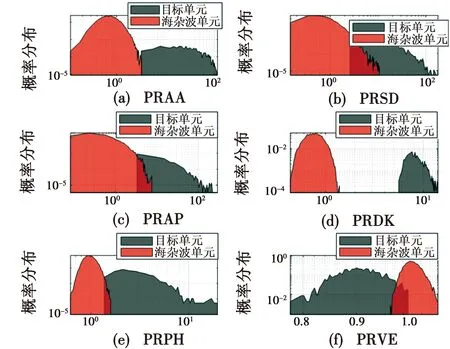
图5 基于全极化信息的特征概率分布直方图Fig.5 Feature probability distribution histogram based on full polarization information

图5结果证明，只有PRDK特征下主目标与纯杂波样本完全分离，而其他特征均有不同程度重叠。

实际应用中，海况等外在因素让单一特征的检测性能无法得到保证，因此，需要多特征融合后进行目标检测，以此使检测算法的鲁棒性更好。

将6个特征组合成特征向量Z，则Z可以表示为

Z=[f1(x)f2(x)…f6(x)]T

(17)

式中,fn(x)计算回波信号样本X的对应特征。假设S0和S1分别表示两种情况下的Z的情况，即

(18)

式中：Zci表示杂波样本对应的特征向量；Zti表示目标样本对应的特征向量；K表示截取的样本总数。为评价Z的可分性，引入巴氏距离[15]。其计算可以看作是S0与S1集合之间的距离，是一种分析可分性的有效方法。特征组合的可分性越强，巴氏距离也就越大，因此，巴氏距离可以把特征组合抽象的可分性量化出来。

为了证明6特征的可分性优势，将本文的特征组合与PCA检测算法的特征组合进行对比，分别计算4种极化模式下在各个数据集上的特征组合巴氏距离，结果如图6所示。

图6 各数据集特征的巴氏距离对比图Fig.6 Bhattacharyya distance of the characteristics of each data set

由结果分析得出：本文选取的特征组合巴氏距离更大，证明了该算法特征组合比PCA检测算法的特征组合具有更好的特征可分性。

同时，为验证本文提出的特征组合比单一极化模式下的特征组合具有更好的性能，计算各个数据集上的巴氏距离，计算结果如图7所示。

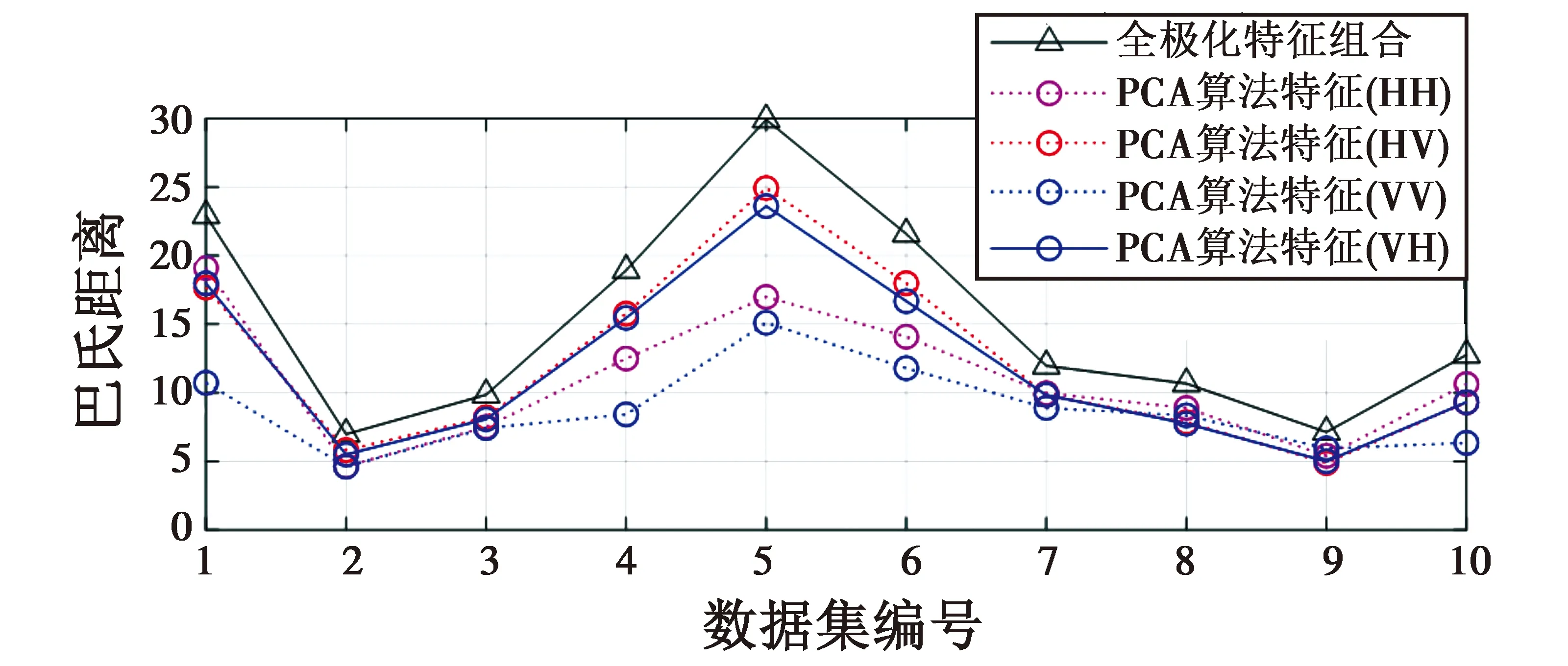
图7 各数据集基于全极化信息的特征巴氏距离对比图Fig.7 Characteristic Bhattacharyya distance of each data set based on full polarization information

选取的6特征组合在全极化信息融合的条件下比单一极化的特征组合具有更大的巴氏距离与更好的特征可分性，更好地保障了算法的鲁棒性与可行性。

2.5 PCA异常检测器

令S为由正常样本特征向量组成正常样本矩阵，即

S=[Zc1Zc2…ZcK×R]

(19)

式中，矩阵S的行为K×R，列为6。令S与待检测样本的特征向量组合新矩阵D，即

D=[ZtiA]T

(20)

式中：矩阵D的大小为M×P，且M=K×R+1，P=6；A为异常样本向量。由于PCA算法性能受到变量尺度影响，因此需要将样本矩阵D先进行归一化处理，即

(21)

s.t.m=1,2,…,M，p=1,2,…,P

式中,σp和μp分别对应矩阵D的第p列标准差以及第p列均值。

(22)

式中，P×P的矩阵C是Dn的协方差矩阵，且

C=UΛUT

(23)

利用奇异值分解得到P×P的正交阵矩阵U，U的列对应矩阵C的特征向量，对角阵Λ的对角线元素λp是C的特征根，且按下列规则排列

(24)

下一步，将样本矩阵Dn降维得到矩阵Y，即

Y=DnUP×j

(25)

式中，前j个特征值对应的特征向量组成了P×j的矩阵UP×j，重构矩阵H及计算样本重构误差，即

(26)

(27)

式中，em为第m个样本的重构误差。按从大到小排序样本重构误差，目标样本的序号是r。对应确定的虚警概率PF，判别准则如下

(28)

最终，算法的整个流程如图8所示。

图8 基于全极化信息的特征融合检测算法流程图Fig.8 Flow chart of feature fusion detection algorithm based on full polarization information

3 实验结果分析

实验过程中需要足够的数据进行算法分析验证，每个数据集在一种极化下的单个距离单元的脉冲数目是217，观测时间1.024 s，脉冲数是1024，用滑动窗口截取1024点数据，滑动窗口大小是128。

实验选取6号数据集，图7结果证明：本文提出的6特征与PCA检测算法中的6特征相比，在4种极化模式下均有着更好的可分性，并且基于全极化的6特征可分性明显优于PCA检测算法在4种极化(HH，HV，VV，VH)模式下的特征可分性。

为了验证本文提出算法的可行性，与GU提出的检测算法(PCA检测算法)[7]相比较，分析检测概率随虚警率变化的曲线。设置虚警率为0.000 1～0.1，计算对应虚警率下的检测概率，得出如图9所示检测概率曲线。

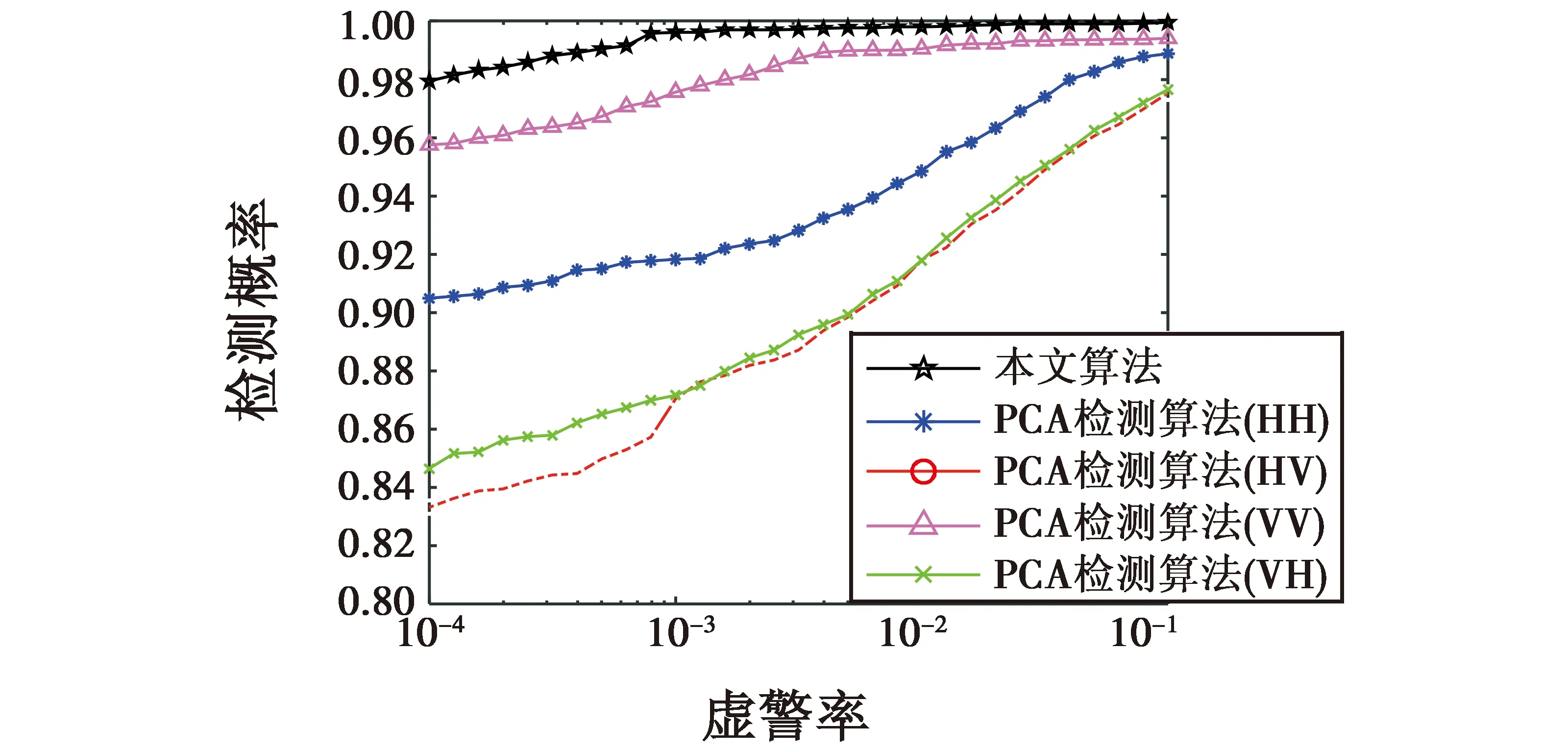
图9 检测器的ROC曲线Fig.9 Reciever operation characteristic(ROC) curves of the detector

从图9可以看出，PCA检测算法的检测性能会因极化模式的改变呈现较大的差异，而相比PCA检测算法(4种极化模式下的检测性能)的检测性能，本文提出的基于全极化信息的特征融合算法性能更稳定，检测概率更高。

4 结束语

针对单一极化模式下，雷达目标检测算法利用信息不充分以及不同极化模式下检测性能不稳定的问题。本文提出一种基于全极化信息的特征融合检测算法，提取了时域以及多普勒域6特征在全极化模式下组成了新的特征检测向量。利用实测数据进行验证，实验分析结果显示本文提出算法的性能更稳定，检测概率更高。