基于分数阶傅里叶变换的声表面波涂层厚度检测

林 滨，杜安尧，刘再蔚，梁小虎

基于分数阶傅里叶变换的声表面波涂层厚度检测

林 滨，杜安尧，刘再蔚，梁小虎

(天津大学机构理论与装备设计教育部重点实验室，天津 300354)

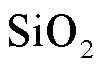
声表面波；频散曲线；分数阶傅里叶变换

声表面波在半无限大单一介质表面传播时，声速仅与介质的力学性质有关；但当传播介质为基体-涂层等非单一介质[1-3]，或近表面存在损伤[4-6]、残余应力等[7-8]状态时就会出现色散现象(不同频率声表面波的传播速度不同)．通过表面波的时域信号获取其时频信息，进而获取频散曲线来反演研究介质的厚度是一种有效且常用的方法．傅里叶变换和小波变换都可以获得声表面波的频散曲线[9-10]，但傅里叶变换在完整地保留频率信息的基础上会丢失时间信息，因此傅里叶变换不能对时变信号进行有效处理；小波变换虽然同时在时域和频域具有一定的分辨率，可以有效地保留信号的时变特性，但小波变换会降低频域的分辨率，且频率分辨率会随着频率的升高而大幅降低；此外小波变换的效果高度依赖于母小波的选取．因此，本文将针对新的频散分析方法进行模拟仿真和实验分析并研究其分析效果．

1 分数阶傅里叶变换时频分析

分数阶傅里叶变换具有多种不同的定义与解 释[11]：线性积分变换、时频面旋转、特征函数与特征值、坐标乘法和求导算子的变换、微分方程的解和超微分算子等．本节仅从线性积分变换对分数阶傅里叶变换进行解释．

1.1 分数阶傅里叶变换理论

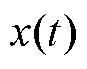
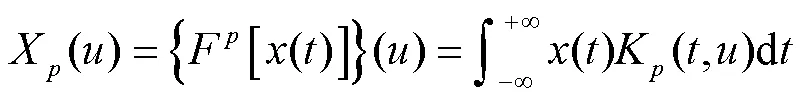
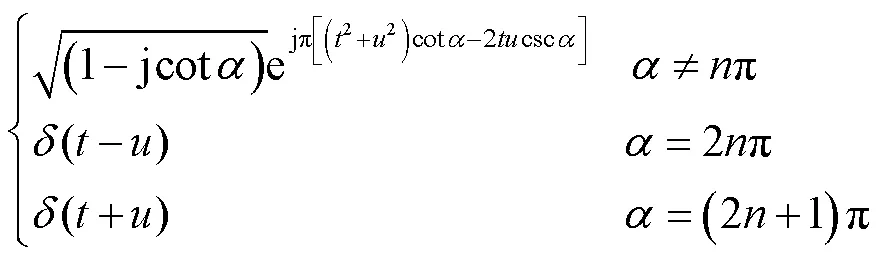
式中为角度参数．和的关系为

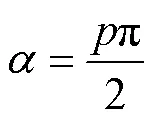
因此可得

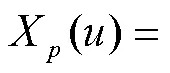
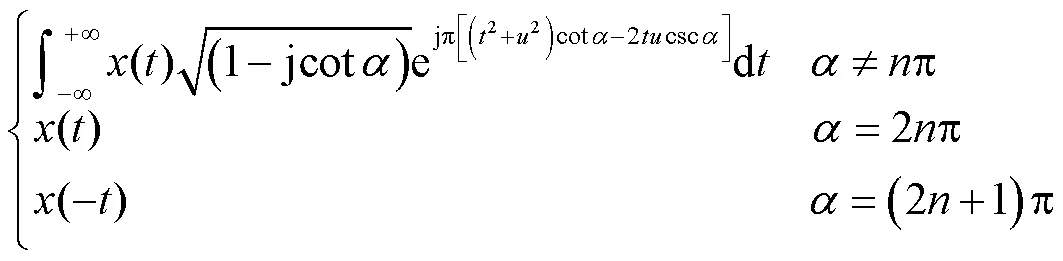
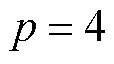
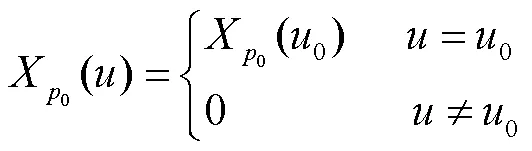
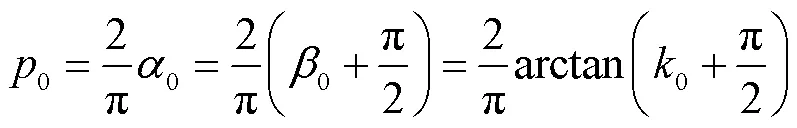
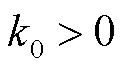
1.2 线性调频函数时频分析

激光激发声表面波可以近似简化为线性调频信号，因此可以利用加入高斯白噪声的线性调频函数来模拟激光激发声表面波，然后利用分数阶傅里叶变换对模拟声表面波进行时频分析，最后将分析效果与小波变换分析效果和理论时频曲线进行对比．

利用瑞利波包构造线性调频信号

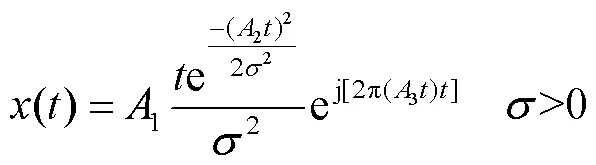
式中：，为幅值参数；，为时间参数；，为调频参数；，为瑞利参数.函数的理论调频率，理论中心频率．为模拟实际实验信号，加入信噪比为－3dB的高斯白噪声，原信号与带噪信号时域波形如图1所示，后续将对带噪信号进行分析．

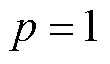
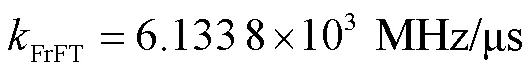
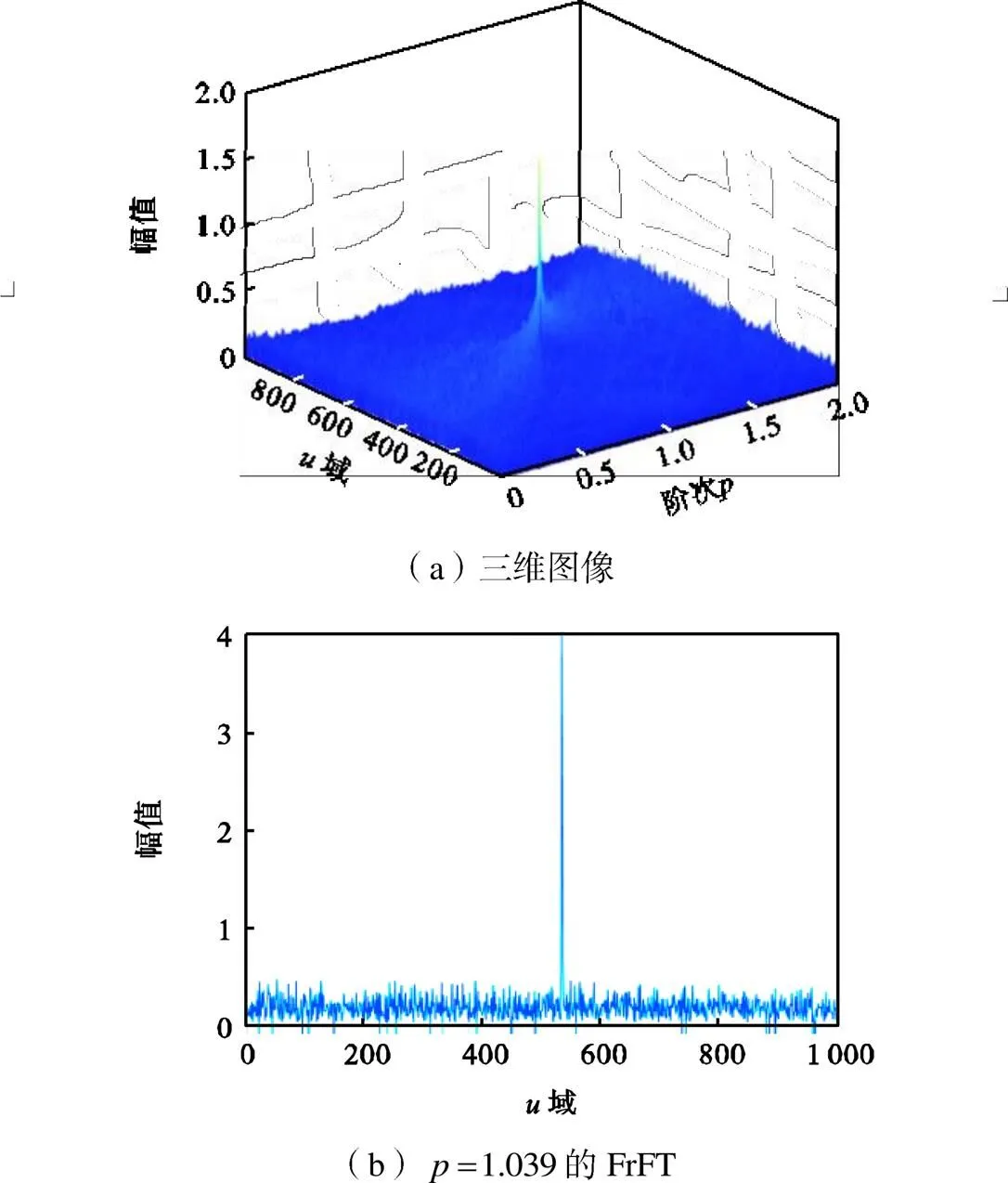
图2 带噪信号的分数阶傅里叶变换

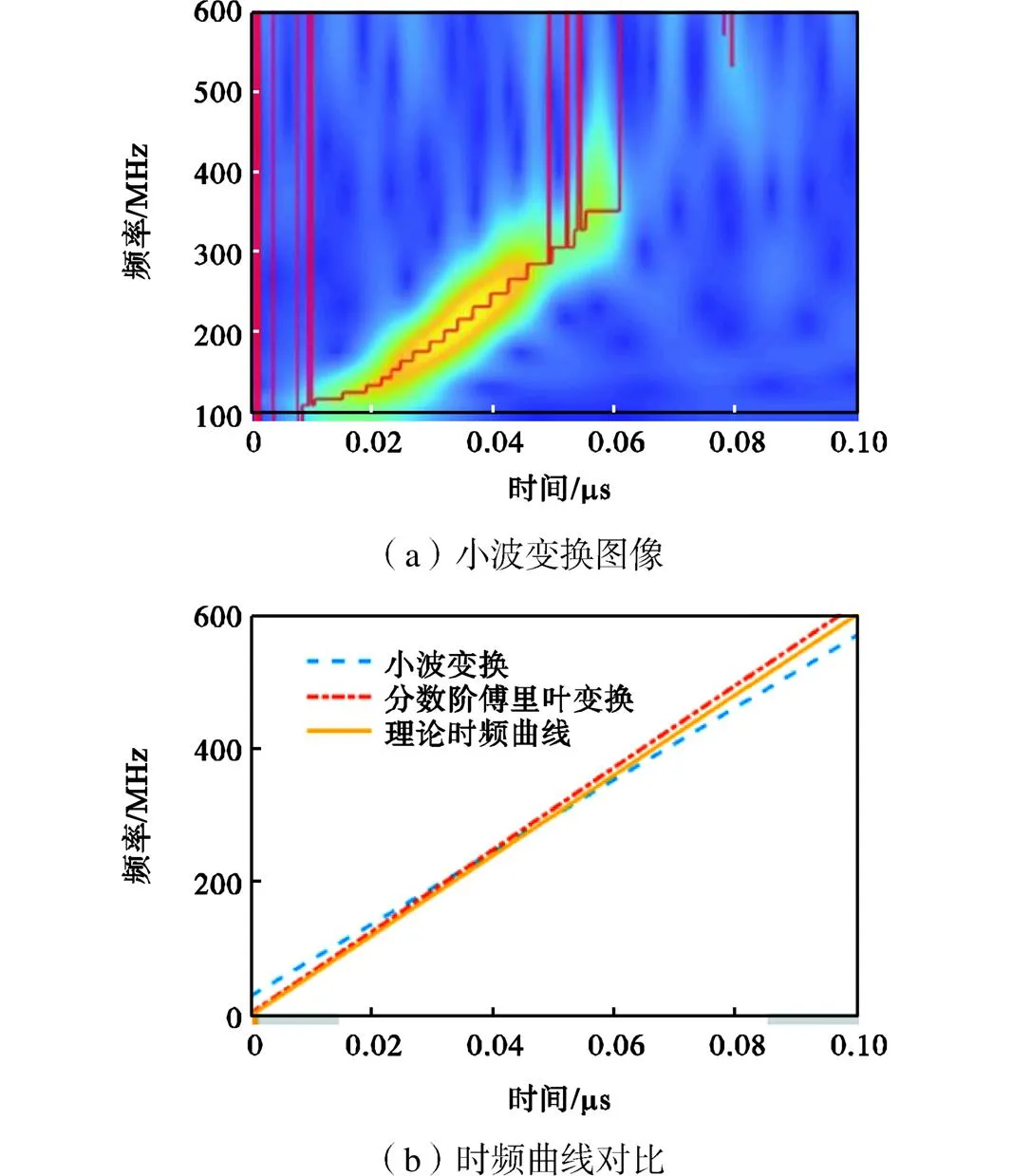
图3 时频分析与对比

2 基体-涂层材料声表面波的分数阶傅里叶变换

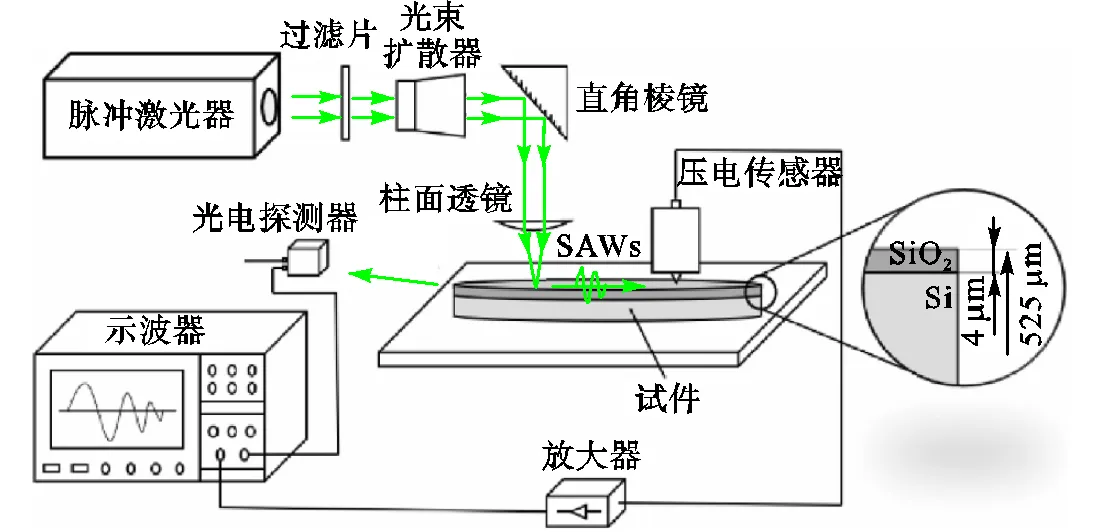
图4 激光激发声表面波实验示意

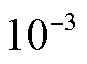
表1 实验材料力学参数

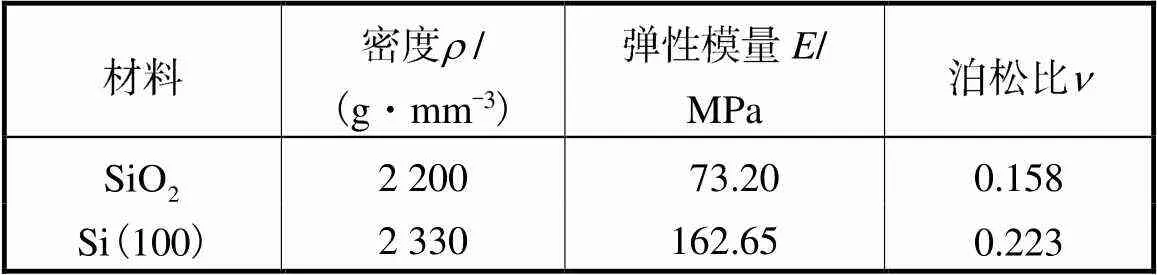
Tab.1 Mechanical parameters of materials

为实现对不同传播距离下声表面波的拾取，将直角棱镜和柱面透镜固接在位移精度0.5μm的直线位移平台上，通过驱动器和编程控制器对五相异步电机的控制使位移平台每次移动1mm，进行3次．需要注意的是，如图6所示，实验过程中激发点需要由远及近向拾取点移动，其目的是为了避免后一次激光激发声表面波传播经过前一次激发损伤区域而受干扰．此外，样品表面上激光激发点和振动拾取点间的距离需要足够大，使拾取点的振动信号为不受热传导影响的稳定声表面波，本实验中激发点与拾取点的距离大于2cm．

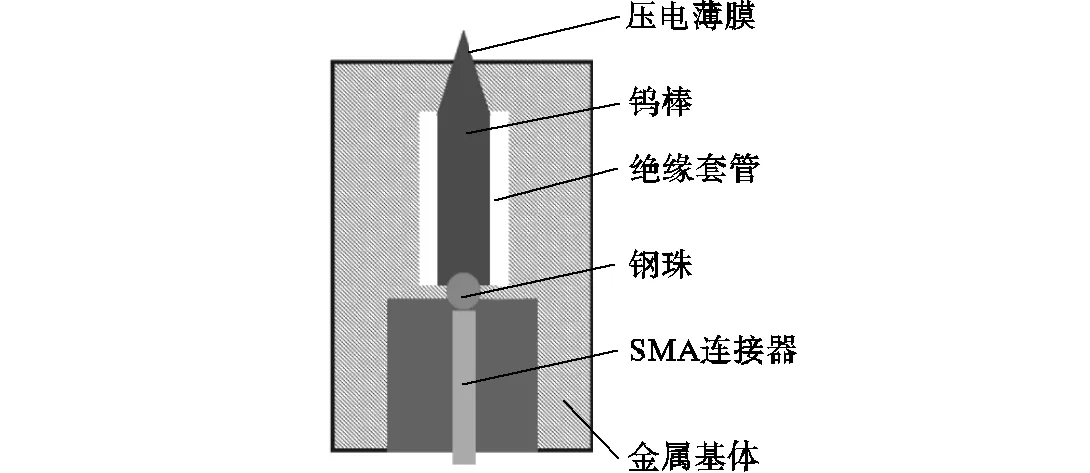
图5 压电薄膜传感器

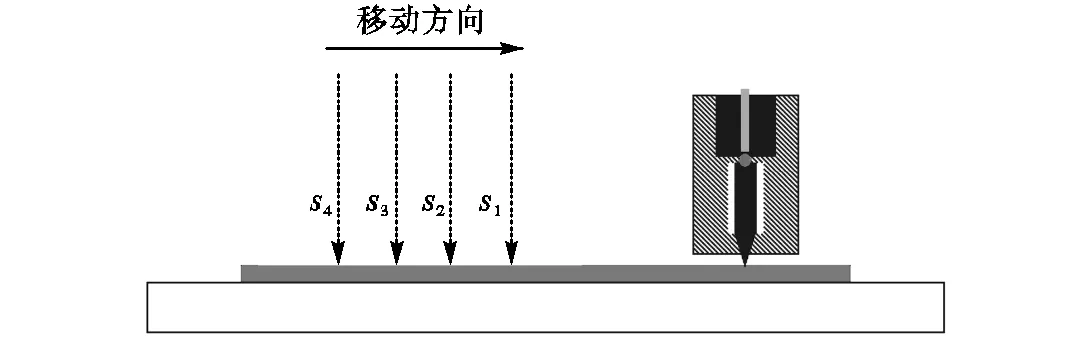
图6 不同激发位置声表面波的拾取

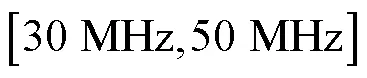
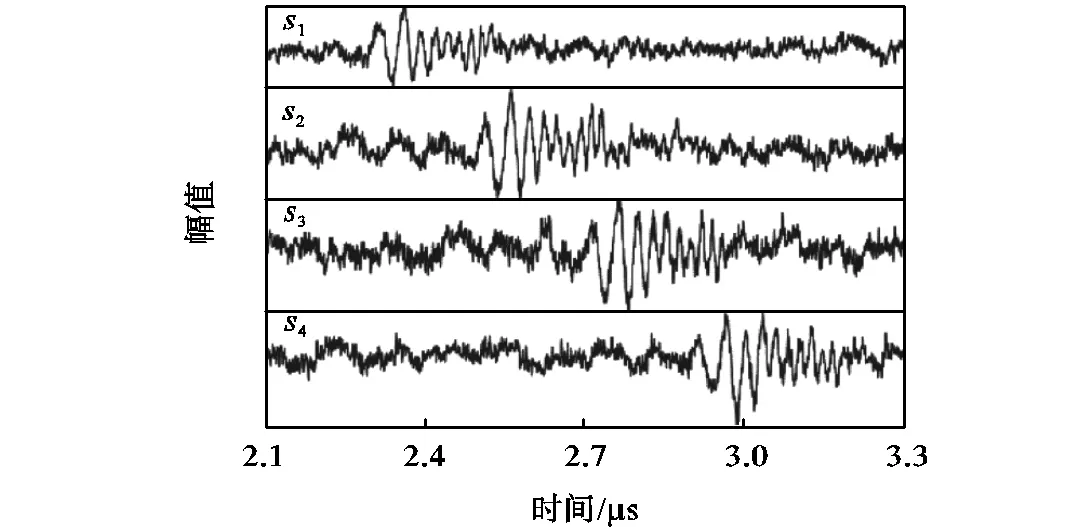
图7 不同拾取点的时域波形

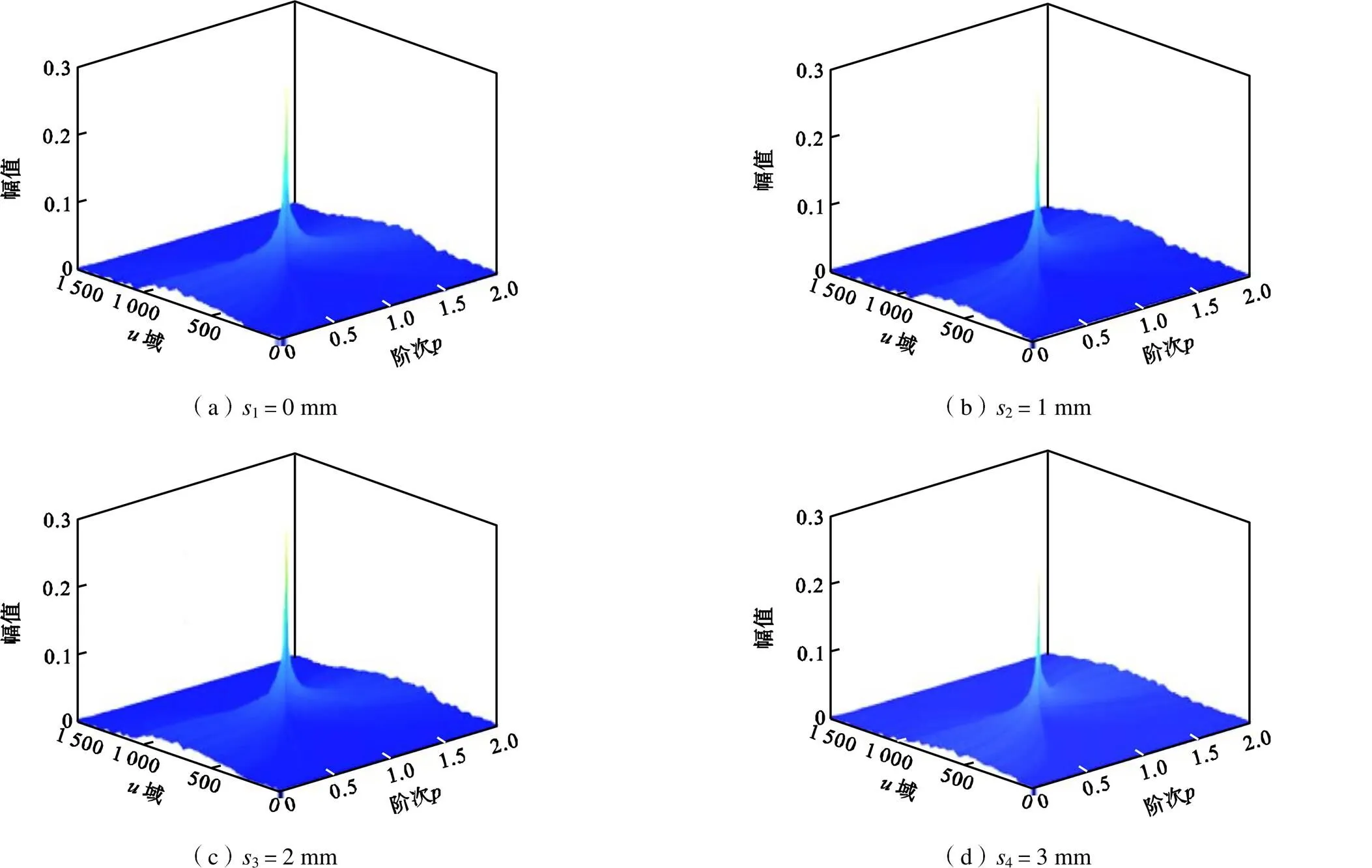
图8 不同拾取点声表面波信号的分数阶傅里叶变换

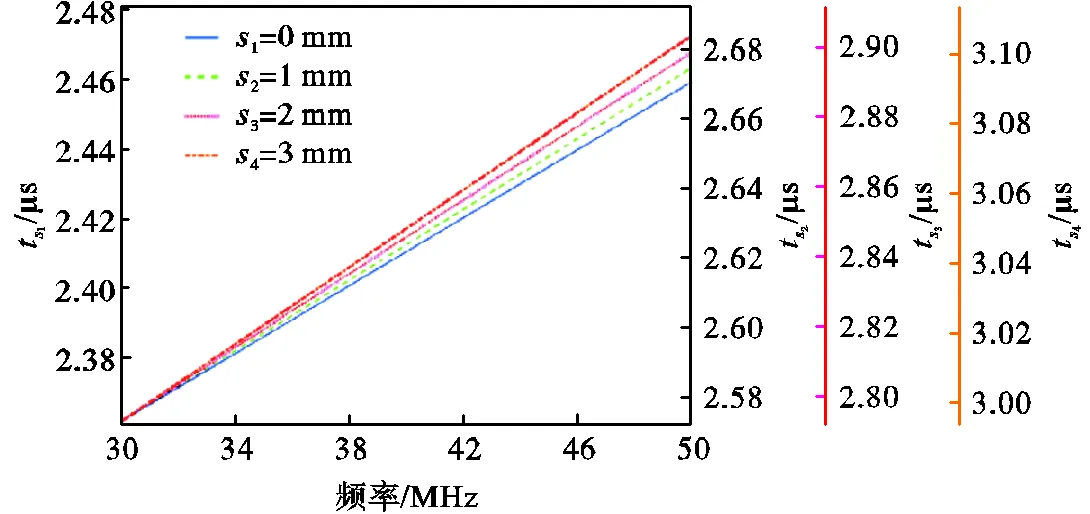
图9 不同拾取点声表面波信号的时频曲线

3 频散曲线反演

因为试件为抛光硅片，表面粗糙度较小，因此可以忽略粗糙度对声表面波频散曲线的影响[16]．在一般情况下，若材料的结构和各部分的弹性常数、泊松比以及密度已知，则可以计算出材料的理论频散曲线．凡友华等[17]提出了标量传递法的相速度频散曲线快速计算方法，但本文中的实验频散曲线为群速度频散曲线，因此利用群速度和相速度的转换关系计算声表面波理论群速度频散曲线，即

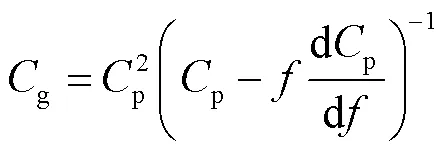
式(9)为半无限大空间单一介质中声表面波群速度近似公式，即

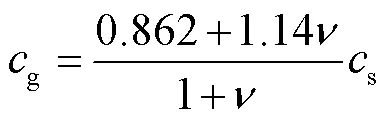
式中：为泊松比；为横波波速，可以通过弹性模量E和泊松比求得．Si(100)和中声表面波群速度分别为4876m/s和3411m/s．图10所示为具有4μm 氧化层的Si(100)的群速度频散曲线，在低频极限时，声表面波几乎在Si(100)基体内传播，其速度接近单晶硅中声表面波速度；在高频极限时声表面波集中于表面的层中，其速度接近于二氧化硅中声表面波的速度．此外，沿着具有4μm 氧化层的Si(100)的[100]晶向传播的声表面波，其频散曲线的拐点在400MPa附近．当频率范围限定在[30MHz，50MHz]时，频散曲线可以近似为一条直线，因此可以通过声表面波时频信息对频散曲线进行线性拟合，进而反演出层的厚度．

在[30MHz，50MHz]的频率范围内，利用式(10)计算声表面波群速度实验频散曲线，即

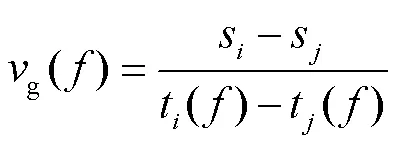
将实验频散曲线与理论频散曲线对比，构造频散曲线失配函数[18]，即

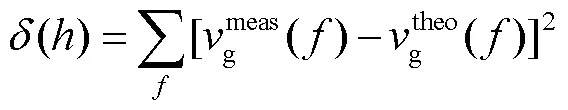
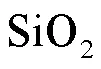
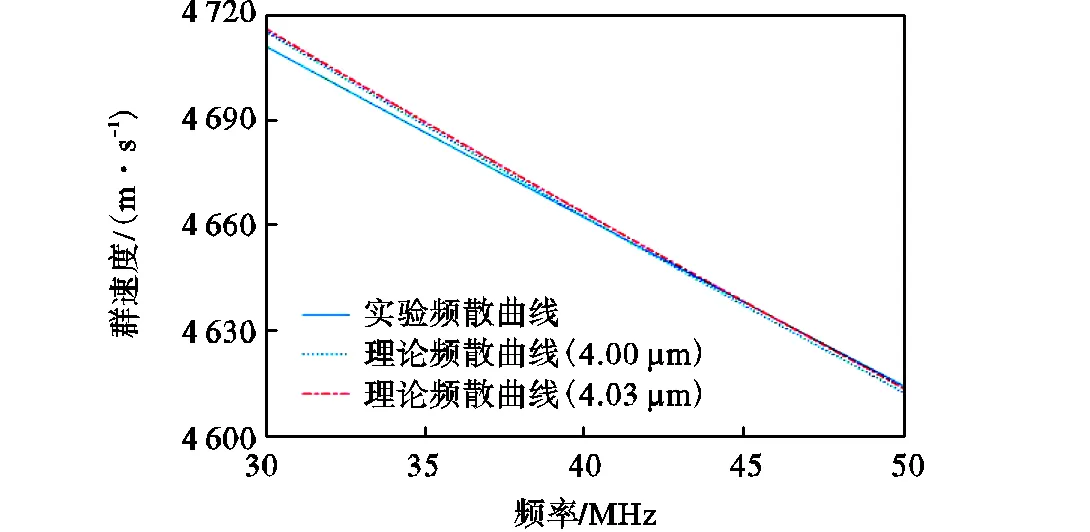
图11 激光声表面波群速度频散曲线

可以看出，反演计算得到的实验频散曲线与理论频散曲线在低频段(小于35MHz)有一定的误差．这是因为原时域信号中噪声引起的误差使得分数阶傅里叶变换之后形成脉冲点的阶次产生一定的误差，这个误差会相应地反映在信号的时频曲线和频散曲线上．此外，声表面波时频曲线和频散曲线本质上都是非线性曲线，对声表面波时频曲线进行线性拟合时也忽略了信号的高阶误差．如要消除图11中35MHz以下频散曲线的误差，就需要在对信号进行分数阶傅里叶变换之前对信号进行去噪处理，此外利用非线性方法对声表面波时频曲线和频散曲线进行拟合也可以降低一定的误差．

4 结 论

声表面波的频散曲线包含了很多被测试件的性质信息，如涂层厚度、弹性模量和泊松比等，因此通过控制变量法来计算频散曲线就可以获得基体-涂层材料的涂层厚度．而在获取声表面波的频散曲线的过程中，对声表面波信号的时频分析是最重要的一步，分数阶傅里叶变换可以有效地对声表面波时域信号进行分析并获取其时频曲线．

(1) 利用瑞利波包和高斯白噪声构造线性调频函数来模拟声表面波信号，并用FrFT和CWT对其进行时频分析．虽然CWT比FrFT具有更低的中心频率误差，但FrFT的调频率误差远小于CWT，因此FrFT更能准确地拟合实际时频曲线．

(3) 利用表面波时频信息计算频散曲线，构造失配函数表征实验频散曲线与理论频散曲线之间的匹配度．通过对失配函数的分析得到实验材料的氧化层厚度为4.03μm，误差仅为0.75%．

［1］ Liu Z，Lin B，Liang X，et al. Time-frequency analysis of laser-excited surface acoustic waves based on synchrosqueezing transform[J]. Ultrasonics，2020，106：106147.

［2］ Ollendorf H，Schneider D，Schwarz T，et al. A comparative study of the mechanical properties of TiN coatings using the non-destructive surface acoustic wave method，scratch test and four-point bending test[J]. Surface and Coatings Technology，1996，84(1/2/3)：458-464.

［3］ Hurley D C，Tewary V K，Richards A J. Surface acoustic wave methods to determine the anisotropic elastic properties of thin films[J]. Measurement Science and Technology，2001，12(9)：1486-1494.

［4］ Moumita M，Amares C，Pulkit K，et al. Effect of initial stress，heterogeneity and anisotropy on the propagation of seismic surface waves[J]. Mechanics of Advanced Materials & Structures，2020，27(3)：177-188.

［5］ Yuan M，Kang T，Kim H J，et al. A numerical model for prediction of residual stress using rayleigh waves[J]. Journal of the Korean Society for Nondestructive Testing，2011，31(6)：656-664.

［6］ Mora P，Spies M. Inversion of residual stress profiles from ultrasonic Rayleigh wave dispersion data[J]. Inverse Problems，2018，34(5)：55001.

［7］ Zerwer A，Polak M A，Santamarina J C. Rayleigh wave propagation for the detection of near surface discontinuities：Finite element modeling[J]. Journal of Nondestructive Evaluation，2003，22(2)：39-52.

［8］ Lavrentyev A I，Veronesi W A，Baaklini G Y，et al. Ultrasonic characterization of shot-peened metal surfaces

[J]. International Society for Optics and Photonics，2001，4336：88-99.

［9］ Liang X，Lin B，Liu Z. Analysis of velocity calculation methods of laser-induced surface acoustic wave[J]. Ultrasonics，2019，100：105985.

［10］ Liu X，Lin B，Liang X. Study of laser-induced surface acoustic wave propagating on materials with machined surfaces based on wavelet analysis[J]. Surface and Coatings Technology，2019，358：173-181.

［11］ Bultheel A，Martínez H. An introduction to the fractional Fourier transform and friends[J]. Cubo—A Mathematical Journal，2005，7(2)：201-221.

［12］ Bultheel A，Héctor E M S. Computation of the fractional Fourier transform[J]. Applied and Computational Harmonic Analysis，2004，16(3)：182-202.

［13］ Ozaktas H M，Arikan O，Kutay M A，et al. Digital computation of the fractional Fourier transform[J]. IEEE Trans Signal Process，1996，44(9)：2141-2150.

［14］ 赵兴浩，邓 兵，陶 然. 分数阶傅里叶变换数值计算中的量纲归一化[J]. 北京理工大学学报，2005，25(4)：360-364.

Zhao Xinghao，Deng Bing，Tao Ran. Dimensional normalization in the digital computation of the fractional Fourier transform[J]. Transactions of Beijing Institute of Technology，2005，25(4)：360-364(in Chinese).

［15］ Bogardus H E. Third‐order elastic constants of Ge，MgO，and fused SiO2[J]. Journal of Applied Physics，1965，36(8)：2504-2513.

［16］ Paehler D，Schneider D，Herben M. Nondestructive characterization of sub-surface damage in rotational ground silicon wafers by laser acoustics[J]. Microelectronic Engineering，2007，84(2)：340-354.

［17］ 凡友华，刘家琦. 层状介质中瑞雷面波的频散研究[J]. 哈尔滨工业大学学报，2001，33(5)：577-581.

Fan Youhua，Liu Jiaqi. Research on the dispersion of Rayleigh waves in multilayered media[J]. Journal of Harbin Institute of Technology，2001，33(5)：577-581(in Chinese).

［18］ Lu Y，Peng S，Du W，et al. Rayleigh wave inversion using heat-bath simulated annealing algorithm[J]. Journal of Applied Geophysics，2016，134：267-280.

Film Thickness Detection Using a Surface Acoustic Wave Based on the Fractional Fourier Transform

Lin Bin，Du Anyao，Liu Zaiwei，Liang Xiaohu

(Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300354，China)

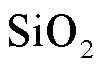
surface acoustic wave；dispersion curve；fractional Fourier transform

10.11784/tdxbz202103050

O426.9

A

0493-2137(2022)07-0714-07

2021-03-24；

2021-05-20.

林 滨（1965—  ），男，博士，教授.Email：m_bigm@tju.edu.cn

林 滨，linbinph@tju.edu.cn.

国家自然科学基金资助项目(52075379).

the National Natural Science Foundation of China(No.52075379).

(责任编辑：王晓燕)