丝驱动连续体机器人的无模型自适应控制

李进华，卜逸凡，李晓阳，宋立栋

丝驱动连续体机器人的无模型自适应控制

李进华1, 2，卜逸凡1, 2，李晓阳1, 2，宋立栋1, 2

(1. 天津大学机构理论与装备设计教育部重点实验室，天津 300354；2. 天津大学机械工程学院，天津 300354)

连续体机器人由于具有高灵活度的特点，被广泛用于微创外科手术、航空、核工业等领域．针对连续体机器人在狭窄、受限环境下的建模误差导致控制精度较低的问题，提出了一种基于无模型自适应控制(MFAC)的连续体机器人末端位置控制方法．首先，对连续体的运动学模型和基于模型的控制方法(MBF)进行了研究，分析了建模误差对连续体机器人运动精度的影响；随后根据连续体机器人的驱动输入与位置输出，实时估计连续体机器人的伪雅可比矩阵，以减弱迟滞、模型误差、外部负载等干扰带来的影响；最后在连续体机器人平台上进行了轨迹跟踪实验，探究了自由状态下连续体机器人末端点的轨迹，随后改变轨迹参数使连续体机器人在不同半径的圆轨迹和不同顶角大小的三角轨迹下进行了轨迹跟踪实验和实验结果比较，并将本文所提出的方法与常见的基于模型的控制方法进行了比较，证明了本文方法具有较好的精度与抗干扰能力．实验结果表明：连续体机器人沿着半径为40mm的圆形轨迹及其内接三角轨迹的均方根误差的平均值分别为2.31mm和2.448mm，具有良好的控制精度，且在运动过程中均方根误差值保持稳定；本文方法的轨迹均方根误差随着连续体运动范围增大而增大，运动精度保持在可接受的范围内；本文方法与基于模型的控制方法相比，可很好地抵抗外部干扰，提高连续体机器人的控制精度．

连续体机器人；无模型自适应控制；雅可比矩阵；轨迹跟踪

连续体机器人是一种受章鱼的手臂和大象的鼻子等生物器官启发的新型柔性机器人[1-2]，具有高灵活性和柔韧性，相较于传统的刚性机械臂，具有质量轻、转动惯量低、运动灵活的特点[3]，可以通过改变自身的形状，实现在狭窄的空间内灵活地变形与移动[4].由于其具有柔性骨架的结构特性，在狭窄空间内操作的过程中，能够保证与环境交互的安全性，目前已经被广泛用于微创外科手术[5-7]、航空[8]、生命救援[9]等领域．

连续体机器人通常需要在狭窄空间内躲避障碍物并到达指定位置[10-11]，为了完成上述任务，需要使用针对连续体机器人操作的控制方法，常见的控制方法有基于模型的控制方法和无模型控制方法．基于模型的控制方法通过使用连续体机器人的运动学模型或者静力学模型来实现对其末端位置控制．Li等[12]推导了连续体的运动学模型，并实现了末端位置的优化控制；Bajo等[13]基于连续体机器人的运动学和静力学模型，提出了一种连续体机器人力-位混合控制方法，实现了对未知柔性环境刚度的估计；Giorelli等[14]将基于模型的控制方法和监督学习进行比较，对非恒曲率连续体机器人进行逆运动学控制；Du等[15]根据连续体的运动学-力学耦合模型，将连续体等效为具有离散关节和刚性连杆的机器人，并对连续体机器人的运动性能进行评价与优化．

由于连续体机器人变形与运动存在耦合，运动学和力学建模误差难以避免，且模型容易受到外部干扰影响．为了进一步提高连续体的控制精度，需要开发对模型依赖较小的控制方法，即无模型控制方法．无模型的控制方法指的是不依赖连续体机器人的数学模型，通过输入、输出数据直接获得其运动学关系的方法．目前国内外许多研究人员已经就连续体的无模型控制展开了研究，Satheeshbabu等[16]提出了一种基于强化学习的无模型控制方法，实现对气动连续体机器人的开环位置控制；Yip等[17-18]基于最优控制实现了连续体机器人无模型控制，并在此基础上实现了无模型力-位控制；Li等[19]将连续体机器人雅可比矩阵变化过程转化为线性随机离散过程，利用自适应卡尔曼滤波对雅可比矩阵进行实时估计；Tan等[20]设计了一种基于调零神经动力学的无模型控制器，仅依靠电机输入和传感器输出即可实现对连续体的控制．上述无模型控制方法在使用过程中存在一些问题：基于神经网络的控制方法计算量较大，获取预训练模型耗费时间，运动精度很大程度上取决于机器人的重复定位精度，且对于外部的干扰抵抗能力较弱；基于卡尔曼滤波的方法稳定性难以保证，对于外界干扰的抵抗能力有限；基于最优控制的方法计算复杂，将严重降低系统的实时性[20]．

为了解决上述问题，本文提出了一种基于无模型自适应控制的连续体机器人末端轨迹控制方法．相较于其他的无模型控制方法具有如下优势：首先，该方法的稳定性可通过理论计算证明，更适用于医疗、航空、航天等对可靠性要求较高的场合；其次，在算法执行过程中，根据输入输出信号实时更新连续体的伪雅可比矩阵，相较于神经网络等方法具有更好的环境适应能力；最后，整个计算过程中无需求解逆矩阵等计算速度较慢的操作，保证了较好的实时性．本文首先介绍了传统的基于模型的正运动学推导过程，建立了从任务空间到驱动空间的映射关系，分析了传统基于模型的方法在求解连续体运动学过程中的缺陷，进而提出了一种连续体机器人无模型位置控制方法，在连续体机器人实验平台上进行了验证并分析了在不同轨迹下的均方根误差．结果表明该方法降低了对连续体机器人精确模型的依赖，提高了连续体机器人的运动控制精度．

1 机器人运动学建模分析

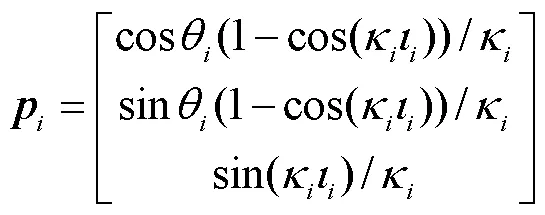
式中：q为连续体在弯曲的过程中沿z轴旋转角度；k为连续体在弯曲过程中的曲率；是连续体中心骨架的长度．

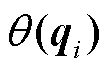
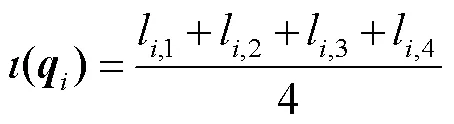
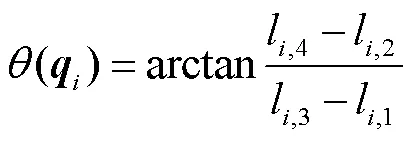
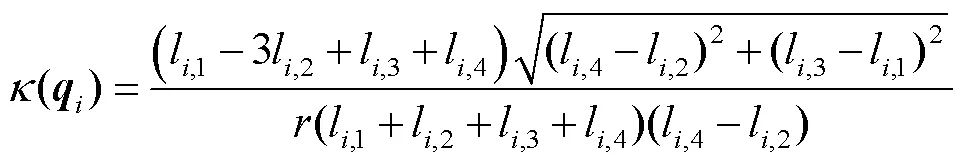
至此，驱动空间到关节空间之间的映射关系可被推导出来．

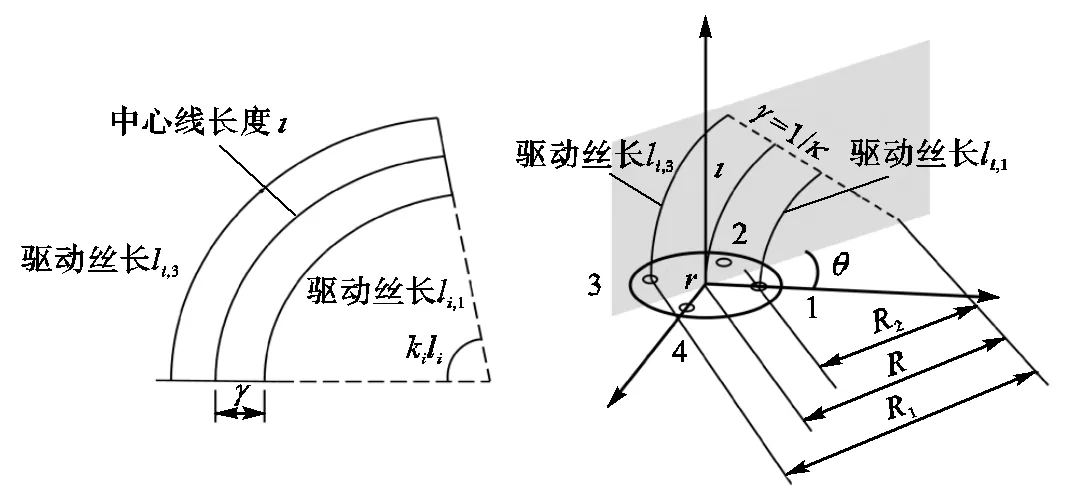
图2 连续体机器人关节参数与丝长几何关系

2 基于模型的连续体逆运动学求解

2.1 基于模型连续体逆运动学

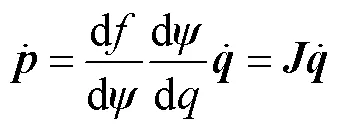
式中、分别为连续体的位置向量和驱动向量．

为获得连续体的逆运动学，需要对雅可比矩阵进行求逆运算，可得到工作空间速度到驱动空间速度的映射关系为

2.2 基于模型的逆运动学的局限性

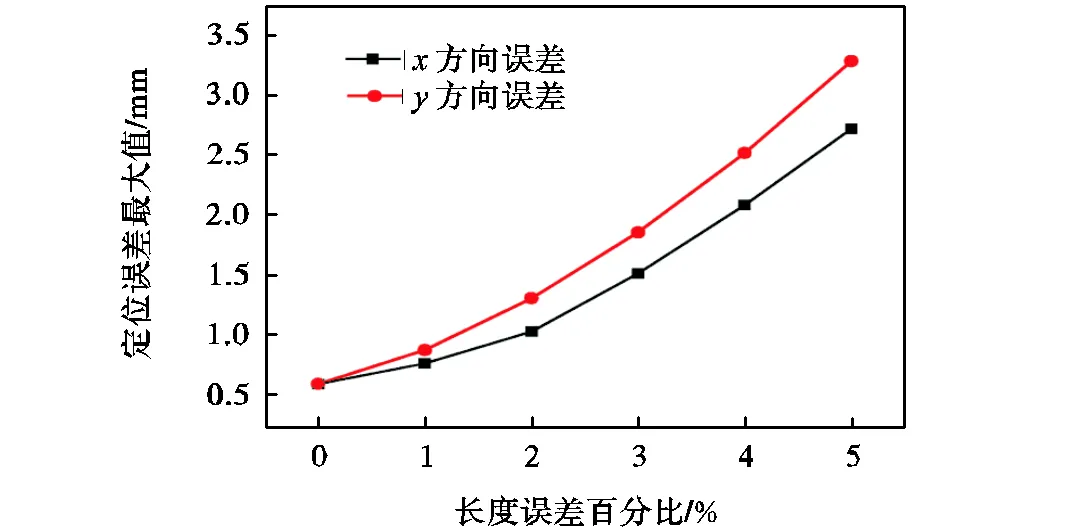
图3 连续体机器人长度误差与末端定位误差最大值关系

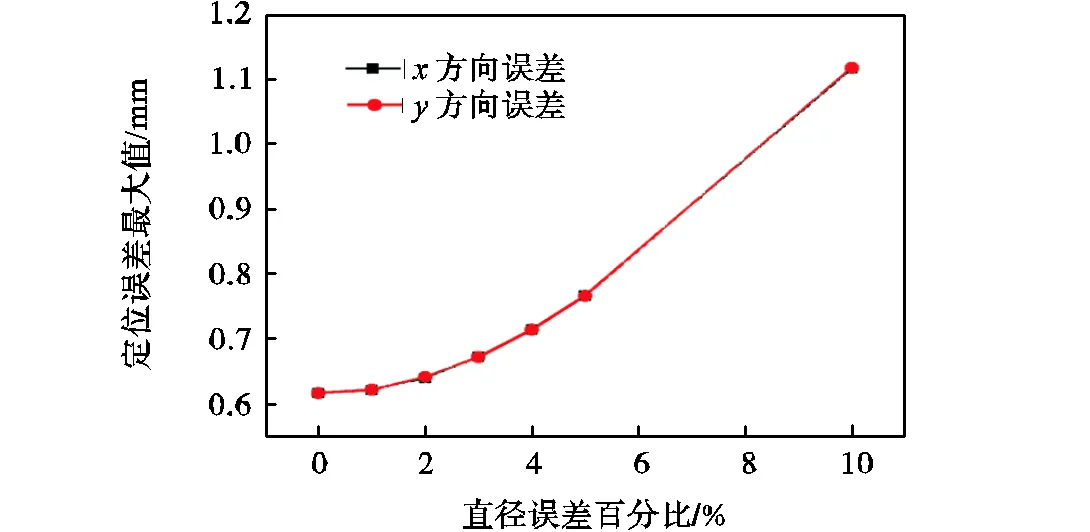
图4 连续体机器人直径误差与末端定位误差最大值关系

从仿真结果可以看出，随着连续体建模中直径与长度建模误差的增大，基于模型的闭环控制方法误差会明显增大．当直径误差为10%时，仿真所得的末端位置误差的最大值从0.62mm增大到1.11mm；当长度误差为5%时，该误差从0.62mm增大到3.28mm；若长度误差增大到10%时，整个迭代求解过程将会难以收敛．

在实际的使用中，连续体机器人建模精度受到恒常曲率简化误差、驱动丝迟滞、参数误差等多种因素影响，会导致基于模型存在很大的建模误差．针对连续体机器人无法获得准确控制模型的问题，需要开发与连续体机器人模型无关的控制方法，以摆脱对于连续体机器人精确模型的依赖．

3 基于无模型自适应控制的连续体逆运动学

3.1 连续体机器人无模型动态线性化

本文提出了一种基于无模型自适应控制的连续体控制方法，通过对连续体机器人的输入和输出信号进行处理，对系统的伪雅可比矩阵进行实时在线估计，获得机器人的运动学模型．无模型自适应控制(MFAC)是Hou等[24]提出的一种数据驱动的方法，该方法的建模过程中仅需系统的输入输出数据即可实现对于系统模型的实时估计，与控制器的模型结构、系统阶数、外部干扰等参数均无关，消除了未建模部分对控制系统的影响．

假设连续体的运动学模型为如下多输入多输出非线性方程：

对于式(9)做出如下假设．

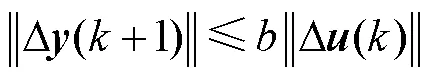
3.2 伪雅可比矩阵在线估计

连续体机器人的逆运动学可以表示为如下的动态线性化模型：

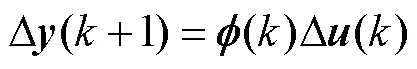
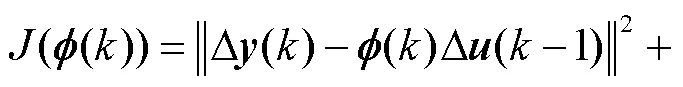
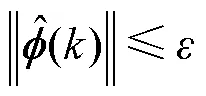
3.3 控制输入在线更新

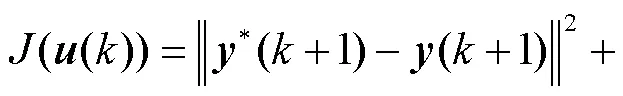
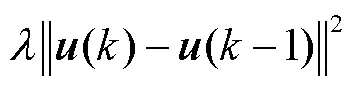
对上述目标函数(15)进行求极值，得到连续体机器人驱动端的控制输入规律如下：

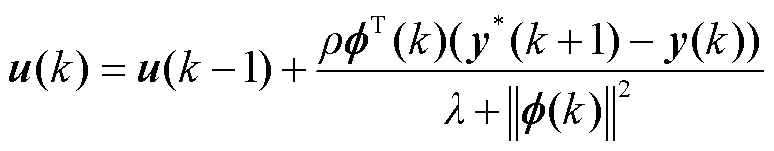
式(16)是在已知期望输出的前提下系统驱动输入的更新方法，可以看出在输入更新的过程中，避免了传统基于模型方法的矩阵求逆过程，有助于降低算法复杂度，提高系统的实时性．

3.4 连续体机器人无模型控制算法设计

式(14)和式(16)分别是无模型自适应控制的伪雅可比矩阵更新和控制输入更新的规律，由此可以建立连续体无模型自适应控制算法，算法流程图如图5所示．

图5 连续体机器人无模型控制流程示意

4 实验结果

4.1 实验平台介绍

在本节中，将所提出的无模型自适应控制方法应用到了丝驱动连续体机器人平台上，并进行算法性能验证．首先计算其自由状态下的轨迹跟随误差，以验证算法的精度．随后在连续体运动过程中施加外部干扰，计算扰动后的轨迹跟随误差和施加扰动后的恢复时间，来证明算法的鲁棒性．

连续体机器人实验平台主要分为上位机、下位机、连续体机器人和光学追踪系统4部分组成，如图6所示．上位机(Windows 10，Intel Core i7@2.8GHz，16G RAM)进行无模型自适应控制计算并将控制信号通过串口通讯发送到下位机(Arduino MEGA 2560)，进而控制步进电机驱动连续体机器人完成相应的动作．实验所用的两自由度连续体长度为150mm，直径为20mm，在连续体末端附加一个光学标记球以测量末端位置．光学追踪系统(NDI Polaris，Ontario，Canada)获取连续体末端位置，将末端位置反馈发送到上位机进行伪雅可比矩阵更新．由于下位机性能有限，整个控制系统的控制周期为10Hz．

图6 实验平台和控制系统

为了量化算法的轨迹跟踪能力，利用连续体末端实际轨迹与期望轨迹之间的均方根误差(RMSE)来评估算法的精度性能[19]，用于定量评价该算法控制下连续体末端轨迹的控制精度．均方根误差的计算公式为

4.2 自由状态下轨迹跟踪误差

为了验证本文所提出的算法在连续体机器人轨迹控制中的有效性，使连续体分别沿着圆形轨迹和三角轨迹进行运动，比较在不同运动轨迹下的轨迹跟踪RMSE值，MFAC控制器参数如表1所示．圆形轨迹(图7)的方程为

表1 MFAC控制器参数

Tab.1 Parameters of the presented MFAC controller

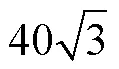
在实验过程中，以连续体机器人的初始点坐标(0，0)分别进行了10次实验．机器人末端沿着圆形轨迹和三角轨迹运动，其对应的轨迹图与轨迹误差变化分别如图7与图8所示．经过分析可得，圆形轨迹的均方根误差平均值为2.31mm，三角轨迹的均方根误差平均值为2.448mm，在轨迹曲率存在突变的情况下，轨迹均方根误差的平均值保持稳定．10次实验轨迹的均方差误差的变化趋势如图9所示．由分析可知：不同轨迹下连续体末端位置的RMES值随着实验进行趋于稳定，在不存在外部负载的情况下，圆形轨迹和三角轨迹的RMSE值将快速收敛到可接受的范围内．

图7 连续体机器人圆形轨迹跟踪结果

图8 连续体机器人三角轨迹跟踪结果

图9 轨迹RMSE值随实验次数变化

图10 轨迹RMSE值随圆形轨迹半径变化

图11 轨迹RMSE随三角轨迹顶角变化

综上所述，本文所提出的无模型自适应控制方法具有良好的轨迹跟踪能力，可使连续体机器人沿着指定的轨迹前进，且在不同的轨迹下控制器的性能均能保持稳定，对轨迹方向发生突然变化的情况具有良好的适应能力，为在环境复杂的实际工况下使用提供了基础．

4.3 与基于模型的方法对比实验

实验结果表明：所提出的MFAC方法在连续体机器人存在较大初始偏转的情况下能够保持较高的控制精度，对外部干扰具有一定的适应能力．在无偏转状态下，MFAC方法比MBF方法精度更高；当存在初始偏转时，MFAC方法在末端轨迹控制精度方面比MBF方法具有明显优势．

图12 外界干扰引起连续体机器人初始末端位置变化

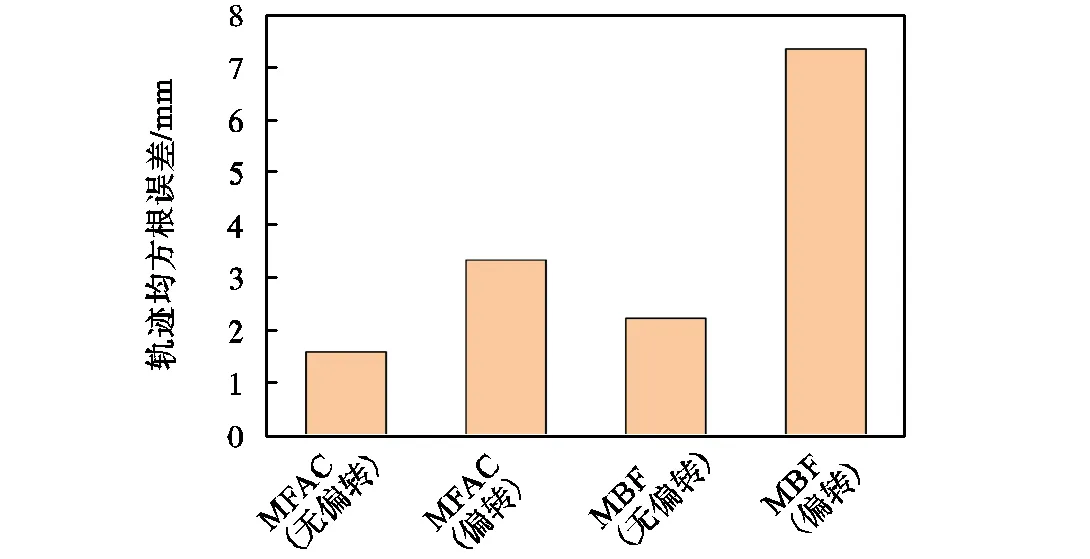
图13 存在初始偏转和无初始偏转状态下MFAC和MBF控制精度对比

5 结 语

本文提出了一种基于无模型自适应控制的连续体末端轨迹控制方法，推导了在连续体运动过程中系统的伪雅可比矩阵和电机驱动向量实时更新方法，实现了连续体机器人的无模型控制，解决在连续体控制中对精准模型存在依赖的问题．相对于传统的基于模型的控制方法，该方法只需要对系统的输入输出信号进行分析，避免了对于连续体长度、直径、末端接触力等参数的测量，直接将模型中的不确定项通过输出和输出直接反映到系统的伪雅可比矩阵中．实验结果表明，该方法在常规情况下具有良好的轨迹精度．本文所做的工作具有广泛的应用前景，目前仅在单关节双自由度连续体平台上进行原理性验证，未来可以在多关节连续体机器人平台上进行应用，验证该方法在负载、避障等方面的性能，并可结合力传感[25]等传感方法，开展控制算法研究．

［1］ Kang R，Branson D T，Zheng T，et al. Design，modeling and control of a pneumatically actuated manipulator inspired by biological continuum structures[J]. Bioinspir Biomim，2013，8(3)：036008-1-036008-14.

［2］ 康荣杰，王 聪，耿仕能，等. 基于雅可比矩阵的连续型机器人灵活性分析[J]. 天津大学学报(自然科学与工程技术版)，2020，53(4)：341-348.

Kang Rongjie，Wang Cong，Geng Shineng，et al. Jacobian-matrix-based dexterity analysis of a continuum robot[J]. Journal of Tianjin University(Science and Technology)，2020，53(4)：341-348(in Chinese).

［3］ Shi C，Luo X，Qi P，et al. Shape sensing techniques for continuum robots in minimally invasive surgery：A survey[J]. IEEE Transactions on Biomedical Engineering，2017，64(8)：1665-1678.

［4］ Burgner-Kahrs J，Rucker D C，Choset H. Continuum robots for medical applications：A survey[J]. IEEE Transactions on Robotics，2015，31(6)：1261-1280.

［5］ Leibrandt K，Wisanuvej P，Gras G，et al. Effective manipulation in confined spaces of highly articulated robotic instruments for single access surgery[J]. IEEE Robotics and Automation Letters，2017，2(3)：1704-1711.

［6］ Li C，Gu X，Xiao X，et al. Flexible robot with variable stiffness in transoral surgery[J]. IEEE/ASME Transactions on Mechatronics，2020，25(1)：1-10.

［7］ 邢 元，牛顺康，金 奎，等. 基于 EM-GRA 方法的机器人辅助手术操作技能评价[J]. 天津大学学报(自然科学与工程技术版)，2021，54(6)：636-644.

Xing Yuan，Niu Shunkang，Jin Kui，et al. Evaluation of robot-assisted surgery skills based on EM-GRA[J]. Journal of Tianjin University(Science and Technology)，2021，54(6)：636-644(in Chinese).

［8］ Wang M，Dong X，Ba W，et al. Design，modelling and validation of a novel extra slender continuum robot for in-situ inspection and repair in aeroengine[J]. Robotics and Computer-Integrated Manufacturing，2021，67：102054-1-102054-11.

［9］ Mcmahan W，Chitrakaran V，Csencsits M，et al. Field trials and testing of the OctArm continuum manipulator[C]// Proceedings 2006 IEEE International Conference on Robotics and Automation. Orlando，USA，2006：2336-2341.

［10］ Qi P，Liu C，Ataka A，et al. Kinematic control of continuum manipulators using a fuzzy-model-based approach[J]. IEEE Transactions on Industrial Electronics，2016，63(8)：5022-5035.

［11］ 康荣杰，刘 跃，耿仕能，等. 丝驱动连续型机器人的建模与避障控制[J]. 天津大学学报(自然科学与工程技术版)，2021，54(6)：651-660.

Kang Rongjie，Liu Yue，Geng Shineng，et al. Modeling and obstacle avoidance control of wire-driven continuum robot[J]. Journal of Tianjin University(Science and Technology)，2021，54(6)：651-660(in Chinese).

［12］ Li M，Kang R，Geng S，et al. Design and control of a tendon-driven continuum robot[J]. Transactions of the Institute of Measurement and Control，2017，40(11)：3263-3272.

［13］ Bajo A，Simaan N. Hybrid motion/force control of multi-backbone continuum robots[J]. The International Journal of Robotics Research，2015，35(4)：422-434.

［14］ Giorelli M，Renda F，Calisti M，et al. Neural network and Jacobian method for solving the inverse statics of a cable-driven soft arm with nonconstant curvature[J]. IEEE Transactions on Robotics，2015，31(4)：823-834.

［15］ Du Z，Yang W，Dong W. Kinematics modeling and performance optimization of a kinematic-mechanics coupled continuum manipulator[J]. Mechatronics，2015，31：196-204.

［16］ Satheeshbabu S，Uppalapati N K，Chowdhary G，et al. Open loop position control of soft continuum arm using deep reinforcement learning[C]//2019 International Conference on Robotics and Automation(ICRA). Montreal，Canada，2019：5133-5139.

［17］ Yip M C，Camarillo D B. Model-less feedback control of continuum manipulators in constrained environments [J]. IEEE Transactions on Robotics，2014，30(4)：880-889.

［18］ Yip M C，Camarillo D B. Model-less hybrid position/force control：A minimalist approach for continuum manipulators in unknown，constrained environments [J]. IEEE Robotics and Automation Letters，2016，1(2)：844-851.

［19］ Li M，Kang R，Branson D T，et al. Model-free control for continuum robots based on an adaptive Kalman filter [J]. IEEE/ASME Transactions on Mechatronics，2018，23(1)：286-297.

［20］ Tan N，Yu P，Zhang X，et al. Model-free motion control of continuum robots based on a zeroing neurodynamic approach[J]. Neural Networks，2021，133：21-31.

［21］ Webster R J，Jones B A. Design and kinematic modeling of constant curvature continuum robots：A review[J]. The International Journal of Robotics Research，2010，29(13)：1661-1683.

［22］ Barrientos-Diez J，Dong X，Axinte D，et al. Real-time kinematics of continuum robots：modelling and validation[J]. Robotics and Computer-Integrated Manufacturing，2021，67：102019-1-102019-12.

［23］ Mo H，Wei R，Ouyang B，et al. Control of a flexible continuum manipulator for laser beam steering[J]. IEEE Robotics and Automation Letters，2021，6(2)：1074-1081.

［24］ Hou Z，Jin S. A novel data-driven control approach for a class of discrete-time nonlinear systems[J]. IEEE Transactions on Control Systems Technology，2011，19(6)：1549-1558.

［25］ Shi C，Tang Z，Wang S. Design and experimental validation of a fiber Bragg grating-enabled force sensor with an ortho-planar spring-based flexure for surgical needle insertion[J]. IEEE Transactions on Medical Robotics and Bionics，2021，3(2)：362-371.

Model-Free Adaptive Control for Tendon-Driven Continuum Robots

Li Jinhua1, 2，Bu Yifan1, 2，Li Xiaoyang1, 2，Song Lidong1, 2

(1. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300354，China；2. School of Mechanical Engineering，Tianjin University，Tianjin 300354，China)

Continuum robots have been increasingly employed in various fields，such as minimally invasive surgery，aerospace，and nuclear industry，due to their high flexibility. A model-free adaptive control-based position control method for continuum robots is proposed in this paper to improve their tracking accuracy in constrained environments. First，the kinematic model-based control method of continuum robots，and effects of the modeling error on the distal positioning accuracy were studied and analyzed. Next，the pseudo-Jacobian matrix of the continuum robot was estimated in real time according to its control input and distal position output signals to reduce external disturbances，such as hysteresis，modeling error，and other interferences. Finally，experiments on the developed continuum robot platform were conducted，and the tracking error for two different trajectories was analyzed in the free space. The comparison between the proposed method and the model-based feedback method indicated that this method had better precision and anti-interference ability. The results showed that the root mean squared error(RMSE)of the continuum robot along the circular and triangular trajectories were 2.31mm and 2.448mm，respectively，indicating the excellent control accuracy of the proposed method and a stable root mean square error value during the tracking movement. The RMSE of the proposed method increases with the expansion of the motion range and remains stable within an acceptable error range. The proposed method considerably resisted external disturbances and improved the accuracy of the control of continuum robots.

continuum robot；model-free adaptive control；Jacobian matrix；trajectory tracking

10.11784/tdxbz202104022

TP242

A

0493-2137(2022)07-0754-10

2021-04-12；

2021-05-31.

李进华（1974—  ），男，博士，副教授.Email：m_bigm@tju.edu.cn

李进华，lijinhua@tju.edu.cn.

国家重点研发计划资助项目(2017YFC0110401)；国家自然科学基金资助项目(51875390，51721003).

the National Key Research and Development Program of China(No. 2017YFC0110401)，the National Natural Science Foundation of China(No. 51875390，No. 51721003).

(责任编辑：许延芳)