“情境-问题”视角下初中数学单元整体教学建构

潘金城 王华

摘要 教师在使用教材时，由于缺乏整体视角，就知识而教知识，使学生的数学学习出现“离位”和“错位”。通过从“学什么、怎么学和为什么学”三个维度聚焦知识、方法和价值，构建初中数学“情境—问题”单元教学模型，针对不同课型设计了“1→n型”“n→1型”“n→n型”“1→1型”四种操作范式，构建了“‘情境-问题双驱动”课堂教学结构流程，通过实践实现了学生学习方式、单元设计思路和学科育人方式等方面的创新。

关键词 情境-问题  单元整体  初中数学

引用格式 潘金城，王华.“情境—问题”视角下初中数学单元整体教学建构[J].教学与管理，2022（13）：41-44.

教材是编写组的专家在基于发展学科核心素养的目标前提下，充分考虑学生生理和心理特征、知识的发展脉络和横纵联系等精心编写而成的。教师在使用教材时，多会遵循教材前后安排的顺序，就知识而教知识，缺乏整体视角，割裂了知识间的纽带，对数学内在的知识体系缺乏深入的研究，对外在的结构关联也不够清晰，从而导致学生只见零碎知识、不见块状知识，只有局部认识、没有整体认识，出现学生数学学习“离位”和“错位”问题。

支离破碎的知识很难有效地发展学生的学科核心素养，当下的数学课堂呼唤以学习为中心的单元教学，教师将单元的知识还原成为知识发生的情境，学生再通过情境提出问题，感悟知识的发生发展过程，从而能动地学习。基于“情境-问题”设计单元教学就是让学生认识更完整的数学。

一、“情境-问题”视角下数学单元整体教学的内涵

一个好的情境至少具备三个条件：一是简洁，二是指向教学本质，三是能生成问题。设置问题情境，提出数学问题，解决数学问题，注重数学应用，简称“情境—问题”。有效的情境与问题应当体现出发展性、开放性、生成性与反思性，在此基础上，从“单元”的角度，结合数学学科特征，“情境-问题”视角的数学单元整体教学内涵界定为：将具有内在联系的教学内容作为独立的教学单元，将不同类型的“情境—问题”用于单元起始课、概念形成课、数学应用课和单元复习课。单元教学可以是一个阶段若干课时，也可以是多个阶段多个课时等。根据“情境—问题”分解单元的知识、方法和价值，明晰单元学什么、怎么学以及为什么学，构建初中数学“情境—问题”单元教学模型（如图1）。

二、“情境-问题”视角下不同课型数学单元整体教学设计范式

素养的形成与解决数学问题息息相关、密不可分。基于此，以建立个体CPFS结构^[1]为主题的单元教学应当是一种发展学生数学核心素养的有效教学模式，对建立知识的整体联系、让学生认识更完整的数学非常有帮助。单元教学以创设情境为起点，让学生提出问题，以问题驱动单元教学的深入开展。针对单元的各种课型，利用“情境—问题”构建不同的操作范式。

1.“1→n型范式”（单元起始课）

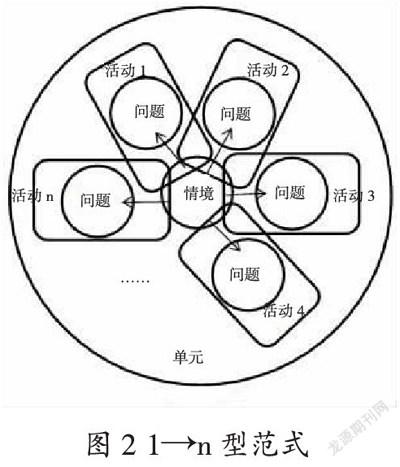
“1→n型范式”就是在一个情境下通过活动提出多个问题，进而解决问题，培养应用意识与创新实践能力（如图2）。此范式主要适用于单元起始课。

例1“分式（章头课）”的教学设计

情境：根据长方形纸张的长、宽和面积关系，探索以下问题。

问题1：表示图3中的未知量“？”，请仔细观察，有哪些是我们学过的？说一说它们之间有什么共同点？与已经学过的哪些代数式有相同点？

问题2：拿出5个同样大小的长方形（长为n，面积为m），按照图4所示的方式拼成一个新的长方形，用不同的方法表示长方形的宽，你有什么数学发现？

问题3：将宽为x，面积为20的长方形纸按图5所示的方式割去一个小长方形，得到一个新的长方形（阴影）面积为16，你能用不同的方法表示出圖中割去部分的“？”吗？

一个情境串联三个问题，通过不同的数学活动探究分式概念、分式基本性质和分式的加减运算，将这三个内容视为一个单元，从整体上感知了本章所学内容，通过类比探究分式概念，建模发现分式基本性质，抽象体会分式加减运算。三大基本思想方法融入其中，“图形直观、数学运算、数学建模”等数学核心素养跃然纸上。王华的文章给出单元起始课教学设计的“类比式、归纳式、组合式和演绎式”等基本方法^[2]。

2. “n→1型范式”（概念形成课）

“n→1型范式”就是通过多个情境和多个相应问题的解决，在将实际问题抽象成数学问题过程中，归纳出它们有共同数学特征，或给出数学定义，或构建数学模型，帮助学生认识理解新单元的数学概念，学习新的单元知识，获得一类问题的解决新方法（如图6）。此范式主要适用于概念形成课。

例2“一次函数（概念课）”的教学设计

情境1：已知汽车的速度是80km/h，你能表示出汽车行驶的路程s（km）与行驶时间t（h）之间的关系吗？

情境2：假设到达加油站时，油箱里的油恰好全部用完，加油枪的流量为25L/min，你能表示出此时油箱的油量y（L）与加油的时间x（min）之间的关系吗？

情境3：先加油再出发，汽车油箱里有油8L，加油枪的流量为25L/min，此时你还能表示出油箱的油量y（L）与加油的时间x（min）之间的关系吗？

情境4：路边有一圆形建筑物，你能表示出圆面积S与半径r之间的关系吗？

情境5：甲地到乙地约10km，你能表示出汽车行驶的平均速度V（km/h）与时间t（h）之间的关系吗？

情境6：每行驶100km耗油9L，出发时油箱里的油只有8L，你能表示出行驶过程中油箱内剩余油量Q（L）与行驶的路程s（km）之间的关系吗？

问题：我们能把这些函数表达式分分类吗？说说你分类的依据。你能再举几个类似这种形式的函数表达式吗？若把因变量和自变量分别用y和x来表示，常数记为k和b，你能用数学式子来表示上述函数吗？

六个情境指向一个核心问题，即一次函数的概念关键属性，让学生经历建模、抽象、归纳等数学思想方法，整体感知了概念的形成过程。采用类似方法，我们可以从单元视角研究“反比例函数”“二次函数”“一元二次方程”等概念，故这种范式对概念的形成教学有着十分重要的作用。

3. “n→n型范式”（数学运用课）

“n→n型范式”通过设计多个情境和相应问题的解决，形成多个并列或递进式的教学活动，帮助学生在知识的运用中形成方法与策略，最终让学生在活动中获得“四基”，发展“四能”，提升“素养”（如图7）。此范式适用于数学运用（应用）课教学。

例3“平分图形的面积（应用课）”教学设计

活动1

（1）情境与问题：观察装有透明长方体盒子中液体体积占长方体容积的比，并提出数学问题。

（2）体验与猜想：改变长方体盒子中液面位置，说说你发现的几何特征。

（3）操作与验证：在长方形纸片上画出所发现的几何特征，并验证猜想。

（4）思考与实践：如图8（1）是否存在过点P的直线，能够平分该矩形的面积？折一折？试一试。

活动2

（1）情境与问题：小明、小丽要平分一块蛋糕[如图8（2）]，该如何切呢？提出数学问题。

（2）思考与操作：画出平分图形面积的直线，并用所给的两个长方形纸片如[图8（3）]组合。

（3）观察与猜想：观察图8（3）的分割线的位置特征，提出你的猜想？

（4）拓展与思考：是否存在不同的平分图8（3）面积的直线？说说你的思考。

每一个情境都有对应的探究任务，每一个问题的设计与解决都与情境有“血脉”关联，或启迪思维发现结论，或激发疑问提出问题。让学生在问题的解决中享受知识“从哪里来？到哪里去？怎么去？”的全过程，数学素养的培育全融于探究过程中。

4. “1→1型范式”（单元复习课）

“1→1型范式”就是通过设计一个情境和相应问题的解决，梳理活动经验和思想方法，帮助学生自然迁移到其他知识模块的问题解决，最终形成方法单元（如图9）。此范式适用于复习教学。

例4“代数推理（专题复习课）”教学设计

活动1 情境与问题

已知实数a满足：a²-3a+1=0.

（1）从这个关系式中，你能得到哪些结论？

专题2—函数中的代数推理

在平面直角坐标系中，已知点（a，b）在一次函数y=2mx+m²+2（m>0）上，且满足a²+b²-2（1+2bm）+4m²+b=0，求m的值。

专题3——几何中的代数推理

在ΔABC中，AB=4，D是AB上的一点（不与点A、B重合），DE//BC，交AC于点E.设ΔABC的面积为S，ΔDEC的面积为S'。探索S'与S之间的大小关系，并说明理由。

问题中涉及了代数推理，主要包括恒等式的证明、条件式求值与证明，以及数量与图形的对应关系。关键在于运算的算理和算法的灵活运用，如整体代换、换元、消元、降次等常见的思想方法。

三、“情境-问题”视角下单元整体数学教学结构流程

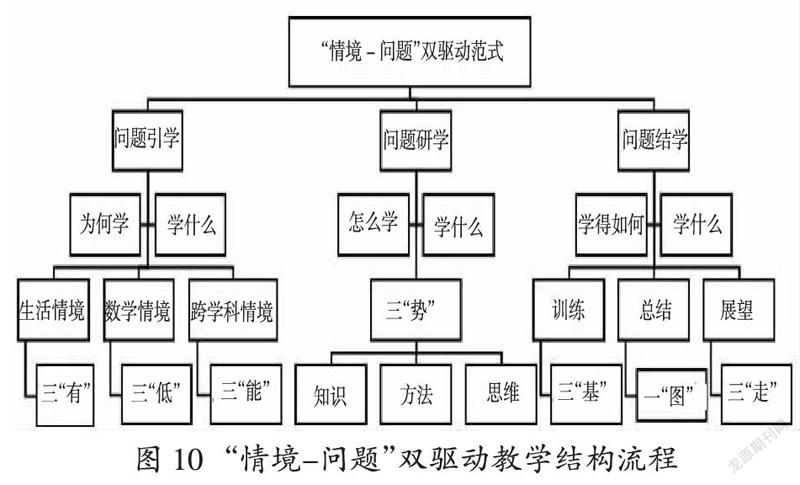
核心问题如同“明灯”，具有方向引领性;核心问题如同“树根”，具有自我生长性;核心问题如同“泉水”，具有连续发展性。“引领性、生长性和发展性”是核心问题的基本特质。由此可见，“核心问题”是数学课堂教学中的灵魂。以“核心问题”为思维载体、“有效情境”为教学导引，融合两者而产生“‘情境-问题双驱动”的教学结构流程（如图10）。

在“问题引学”中，生活情境要体现三“有”，即生活情境要“有意思、有意义、有意味”;学科情境要体现三“低”，即问题设计要“知识起点低、理解起点低、练习起点低”;跨学科情境体现三“能”，即问题情境要“能提出数学问题、能简化复杂背景、能引导自主发现”。在“问题研学”中，通过“逆势、顺势和造势”三种生长方式将核心问题加以转换，让学生深度体验“知识、方法和思维”价值，培养“理解、迁移和创新”素养。在“问题结学”中，训练内容要重视三“基”，即内容的选择要“基于课标、基于素养、基于可选择”;课堂小结通过“思维导图”，纵向上通过知识梳理力求内容的全面性，横向上通过建立联系力求思维的深刻性;学习展望要关注三“走”，即通过学习反思后让学生期待探究新问题，从而引领学生“走向新知”;通过习得新知后主动关注联系生活问题，从而引导学生“走向生活”;通过经历探究后可能产生的疑难问题，从而引发学生“走向研究”。“情境—问题”视角下的教学评价中“数学维度”和“情境维度”分为“理解、迁移、创新”三个水平进行表述^[3]。

“1→n型”“n→1型”“n→n型”“1→1型”是单元整体教学设计的基本范式，是課堂教学不可或缺的“芯片”。而“‘情境-问题双驱动”的教学结构则是组织教学的流程导向，是基本范式在课堂教学的实践场域。两者分别在教学设计与实施中起到重要作用，密不可分。

四、“情境-问题”视角下单元整体数学教学实践创新

1.从“活动—思考”走向“情境—问题”，改变学生学习方式

数学的学习需要学生经历一系列的活动，从而引发学生的思考，增进学生的理解。在“情境—问题”视角下，教师提供一些与数学相联系的真实情境，引导学生提出问题、质疑反驳、解决问题、数学应用。从“活动—思考”走向“情境—问题”不是摈弃“活动—思考”，而是让学生经历真实情境，改变那些盲目的活动，使学生获得活动的价值，让学习真实发生，增加学生数学学习的兴趣。

2.从“教材秩序”走向“学习秩序”，改进单元设计思路

教材编写注重突出核心内容，注重内容之间的相互联系，有自己的编写逻辑，展示数学知识的整体性和数学方法的一般性。为帮助学生自觉感悟数学知识之间存在的逻辑顺序，依托义务教育阶段初中数学内容，在课程标准框架下，以教材为基础，从提升学生数学核心素养的角度出发，用系统论的方法引导教师对教材进行重组、优化设计，形成教学单元，通过分析单元中的事实性知识、方法性知识和价值性知识，让学生明晰学什么、怎么学、为什么学，实现从“教材秩序”走向“学习秩序”。

3.从“知识获取”走向“素养发展”，改善学科育人路径

“问题-情境”下的教学主要表现在对目标重构、内容改造的过程中，表现在对教学全流程中各个环节的设计上，表现在对教学的组织和实施上。学生的学习主要表现在学生在教师所重构的教学体系下自然地展开自主学习与合作学习，表现在学业质量水平的提升上，表现在数学核心素养的达成上。

指向核心素养的教学在“力求真情境、追求真探究、以求真思维”目标下培育学生必备品格和关键能力。而“情境-问题”视角下的数学单元整体教学正是聚焦有效情境，创设有效问题，凸显整体观念，发展学生数学核心素养，真正为学生认识更完整数学提供有效路径。

参考文献

[1] 喻平，李渺，杨义莹.个体CPFS结构与探究问题能力的关系研究[J].数学教育学报，2006（03）：41-45.

[2] 王华.数学单元起始课教学设计的原则和方法[J].教学与管理，2020（07）：39-42.

[3] 魏亚楠，严卿.数学核心素养理念下对情境问题的思考与设计[J].教学与管理，2019（03）：81-84.

【责任编辑  郭振玲】

*该文为2020年江苏省中小学课程基地与学校文化建设项目“‘做·探·创数学学科示范中心”、江苏省教育科学“十三五”规划课题“‘情境—问题视角下初中数学单元教学设计研究”（B-b/2018/02/149）的研究成果