考虑区域占有率的RTCN路内停车泊位预测模型

徐建闽，朱琳聪，马莹莹

(华南理工大学 土木与交通学院， 广东 广州 510640)

0 引言

停车问题已经成为城市交通管理中的重要问题之一，停车位有限导致路上行驶的许多汽车会出现反复寻泊[1]的现象，道路上的许多汽车在寻找停车位时消耗了很多时间和资源。向公众提供准确的实时以及预测的停车位信息，可提高整个停车系统的运行效率，减少车辆的反复寻泊进而降低城市路网中的无效交通量。

近年来，深度学习在短时空闲泊位数预测中得到广泛应用。曹智慧[2]提出用BP神经网络预测技术来进行空闲泊位数的预测。梅杰[3]分析了影响空闲泊位数变化的因素，提出了基于LSTM神经网络的预测技术。Tamrazian等[4]使用无监督机器学习算法对校园内的停车数据离线和在线预测，神经网络模型具有较强的适应性及较好的预测性能，已成为空闲泊位数预测中的常用方法，但是容易陷入局部最优，预测结果有一定的波动和随机性。季彦婕等[5]利用小波变换对空闲泊位数数据进行重构，以粒子群算法对模型的参数进行优化，提出组合预测模型。卢旭旺[6]提出一种基于GRU结构的RNN算法，通过比较不同RNN结构的预测性能确定网络的最佳结构。佘飞等[7]为了提高大型停车场空闲泊位数预测的精确性，提出了灰色理论、BP神经网路以及马尔科夫链的组合预测算法。刘菲等[8]基于LSTM模型和Bi-LSTM模型建立了优化LSTM模型，将LSTM模型的输出作为Bi-LSTM模型的输入，Bi-LSTM结合了正向LSTM模型和逆向LSTM模型的优点，进一步提高预测精度，组合预测算法能够有效避免神经网络预测陷入局部最优，具有较强的全局搜索能力，但是容易发生梯度爆炸和梯度消失，导致预测效率降低。

卷积网络应用于序列预测已经数十年了，卷积神经网络(convolutional neural network，CNN)可用于捕获空间特征[9]，而递归神经网络(recurrent neural network，RNN)可用于捕获时间特征，神经网络的变体和混合模型也广泛应用于空闲泊位数预测领域。赵聪等[10]利用卷积长短时神经网络(ConvLSTM)，构建动态管理模式下路内停车泊位占有率预测方法，通过实验证明有政策的模型预测精度显著上升。

当前有关数据驱动的空闲泊位数短时预测的研究中，RNN模型仍然占据主流地位[11]，在涉及CNN模型的研究中，多数卷积网络被作为辅助手段，并没有充分发挥出时序卷积神经网络的性能优势。针对空闲泊位数预测问题，为了解决CNN模型存在的梯度消失、梯度爆炸以及训练效率等问题，本文提出使用TCN模型。TCN模型是由Bai等[12]于2018年提出的，是基于WaveNet模型的改进。根据对现有文献的研究，TCN模型尚未用于空闲泊位数预测，且尚未引入RAdam优化器进行优化，当前改进的时序卷积模型虽然在时间序列领域表现良好，但是未考虑空间相关性特征。本文将提出一种考虑区域占有率的基于改进TCN算法的空闲泊位数预测方法，将空间因素引入改进TCN模型中，旨在使得模型拥有更加准确的预测值。

本文的创新点主要有：

①为了解决空闲泊位数预测时间特征提取问题，将TCN模型应用到空闲泊位数预测领域；

②为了解决路内停车样本数过少的问题，利用RAdam优化算法对TCN模型进行改进，提高空闲泊位数预测模型的预测精度；

③为了充分考虑到周围停车状况对路内停车路段的影响，提出区域占有率，通过计算空闲泊位数和区域占有率的相关系数得出区域占有率对路段空闲泊位数有影响这一结论，并将其引入空闲泊位数预测模型，进一步提高模型的预测精度。

1 空闲泊位数时间空间特性分析

1.1 时间特性分析

选取广东省深圳市南山区路内停车位位研究对象，对2018年11月5日—25日的空闲泊位数进行分析，分析时间段工作日为7：40—20：00，非工作日为10：10—20：00。广东省深圳市南山区路内停车空闲泊位数变化图如图1所示。由图1可见，深圳市南山区路内停车的空闲泊位数具有一定的规律性。通过散点图观察发现，工作日的空闲泊位数日变化趋势有极高的相似性；但是，由于非工作日休闲出行的增多，因此非工作日的空闲泊位数与工作日有明显差异。

总的来看，空闲泊位数变化既存在一定的规律性又存在一定的随机性，对于时间序列问题，基于卷积神经网络的时间序列预测模型(TCN)已经得到越来越广泛的应用，利用TCN算法构建预测模型，是实现短时空闲泊位数预测的重要方法。

图1 广东省深圳市南山区路内停车空闲泊位数变化图Fig.1 Changes of free parking spaces on the road in Nanshan District

1.2 路内停车位空间特性分析

深圳市南山区停车数据涉及26个路段，共计1 107个停车位。PFLÜGLER等[13]认为位置和交通状况是影响空闲泊位数的重要因素，从逻辑上看，路内停车位会受到附近路内停车路段的影响，如果附近路内停车位较为紧张，那么该路段的停车位也会受到影响。

本文针对深圳市路内停车数据进行分析，提出引入区域占有率作为描述路内停车路段的空间属性，并以此来对停车区域进行划分，即以目标路内停车路段为中心，以整个区域内路内停车占有率为属性，选择适当长度的半径画圆进行区域划分，停车区域划分方式如图2所示。参考文献[14]对停车区域的划分，以空间距离为考虑因素，并以3个路内停车路段为例进行区域划分。

R(n)表示以路内停车路段为圆心，半径为r的区域内泊位占有率，表达式为

(1)

式中：k为区域内的路内停车路段数量；Xi为第i个路内停车路段的停车数量；Pi为第i个路内停车路段的停车位数量。

图2 停车区域划分Fig.2 Area division around the parking

在考虑将区域占有率引入空闲泊位数预测模型前，需分析区域占有率和空闲泊位数的相关性，协方差关系是分析2个变量相关性的经典方法，公式为

(2)

式中:X为区域占有率时间序列；Y是路内停车路段空闲泊位数时间序列；E[X]和E[Y]是2个时间序列的期望值; Cov(X，Y)为相关系数。

经过公式(2)计算，区域占有率时间序列和路内停车路段空闲泊位数时间序列的协方差为-0.73，协方差在-0.5～-1.0，可以看作对路内停车路段空闲泊位数有重要影响。

2 预测模型

2.1 TCN模型结构

由于传统神经网络模型存在收敛速度慢，容易发生梯度消失或梯度爆炸等问题，因此Bai等[12]提出一种新型神经网络模型TCN模型。TCN模型主要由因果卷积、空洞卷积以及残差连接3部分组成。

2.1.1 因果卷积和空洞卷积

TCN使用一维全卷积网络(FCN)架构[15]的因果卷积，然而一个简单的因果卷积只能回顾网络深度范围内的线性历史记录，使得该因果卷积在应用于需要较长历史信息的序列任务时具有挑战性，所以采用空洞卷积对模型进行改进。对于一维序列x∈Rn以及卷积核f:{0，1，…，k-1}→R，将序列元素S上的空洞卷积运算F定义为

(3)

式中:d为空洞系数；k是卷积核大小。

因此，空洞卷积的原理是间隔采取信息，以获取更大历史范围内的数据，空洞系数d决定了采样率，空洞系数即为采样间隔，空洞系数越大，输入的历史范围越大，有空洞系数的因果卷积如图3所示，空洞系数d=1，2，4，卷积核大小k=3 。

图3 有空洞系数的因果卷积Fig.3 A dilated causal convolution with dilation factors

2.1.2 残差连接

尽管使用了空洞卷积，有的模型可能依旧非常深，较深的网络结构会发生梯度消失等问题，所以引入残差连接。2016年，He等[16]提出了一个残差的学习框架，以简化网络非常深的网络训练，该学习框架是ResNet网络结构，利用残差块不仅增加了网络深度，而且还提高了准确度，该残差块包含一个分支，该分支通过一系列变换F，其输出和x被添加到激和函数的输入中，o为激活函数的输出结果。

(4)

2.2 RAdam优化算子

由于路内停车泊位数数量有限，存在样本不足的问题，因此RAdam优化器解决了Adam优化器预热期样本不足的问题，将RAdam优化器应用于空闲泊位数预测能有效解决样本不足的问题，提高预测精度，加快训练速度。

RAdam算子流程如下：

输出：优化后参数θt；

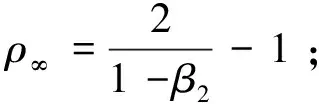
Step 3：如果方差是可处理的，例如ρt>4 ，那么执行Step 4，否则执行Step 5；

2.3 空闲泊位数预测模型

2.3.1 构建空闲泊位数预测模型

短时空闲泊位数预测模型以空闲泊位数为预测目标，通过时间块结构来充分提取空闲泊位数的时间特性，RTCN模型架构如图4所示。第一层是空闲泊位数序列输入层，接下来是连续堆叠的4层残差块，每个残差块由2层空洞因果卷积、非线性映射函数使用修正线性单元(rectified linear unit，ReLU)和1×1卷积组成，卷积核的大小是4，卷积核个数是10，每层残差块的空洞系数为1、2、4、8，之后是全连接层，最后是输出层，输出目标时刻的空闲泊位数。

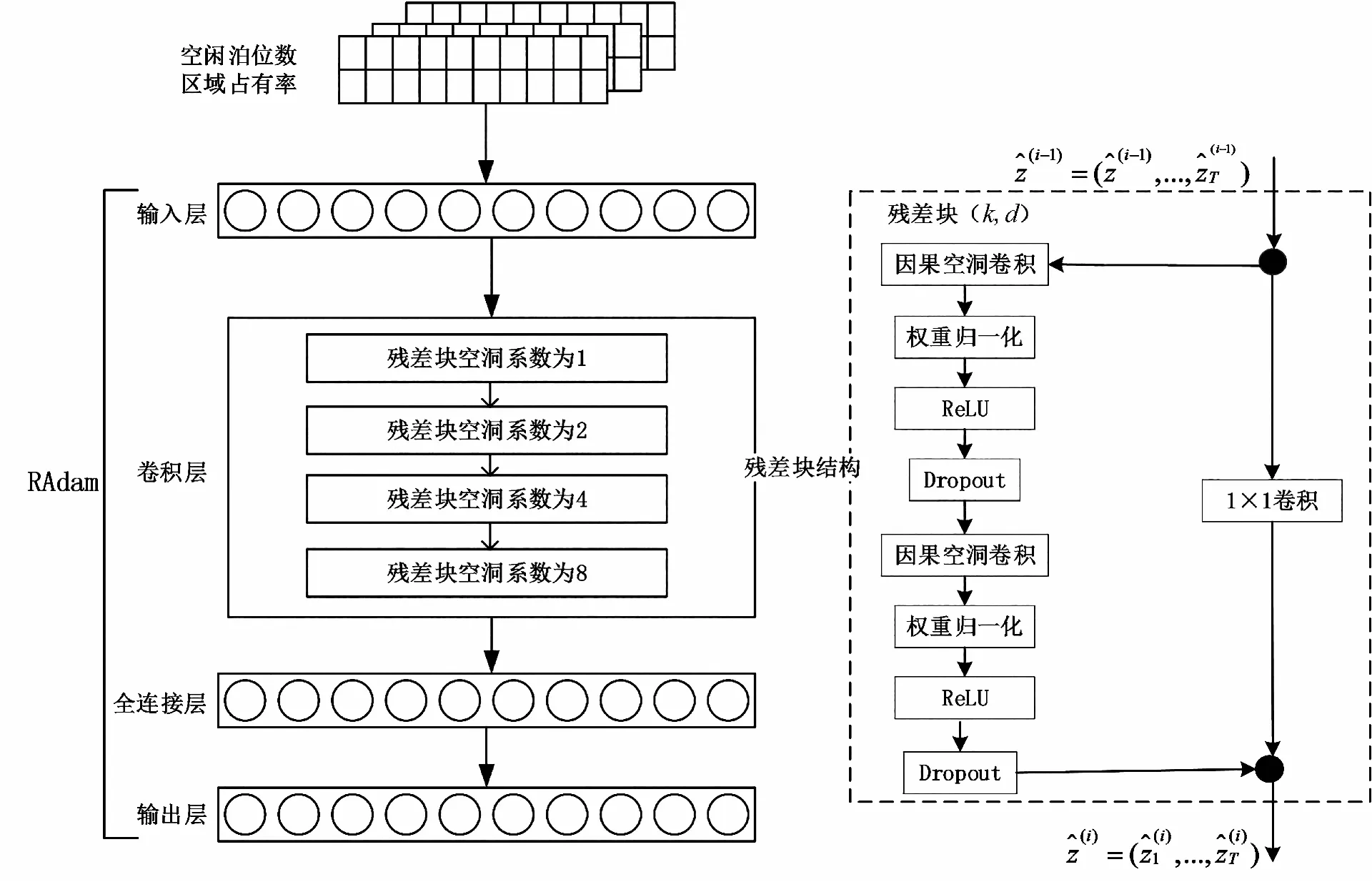
图 4 RTCN结构Fig.4 RTCN architecture

2.3.2 空闲泊位数预测步骤

图5 空闲泊位数预测步骤Fig.5 Steps of prediction of free parking spaces

具体步骤如下：①进行数据处理，剔出异常值；②停车区域划分，计算每个路内停车路段的区域占有率；③基于改进TCN模型对空闲泊位数进行预测；④引入区域占有率特征对空闲泊位数进行预测；⑤模型评价。

2.4 预测结果的评价指标

为了比较不同预测方法的准确性，以均方根误差(root mean squared error，RMSE)和平均绝对误差(mean absolute error，MAE)为主要指标。RMSE和MAE分别用来评价预测值和真实值之间的误差以及预测值和真实值之间的差值，分别用R、M表示，评估指标表达式为

(5)

(6)

3 算例分析

3.1 数据划分

本文中实验数据来源于深圳市政府数据开放平台，随机挑选3个不同区域的路内停车路段，分别是高新南七道、海德一街和科技南街，3个停车路段均为全日泊位类型，工作日7：30—20：00收费，非工作日10：00—20：00收费，不限停车时间。训练数据为2018年11月5—25日(7：40—20：00)的空闲泊位数，并且20%作为验证集，对工作日(2018年11月26—31日)7：40—20：00与非工作日(2018年12月1—2日)10:10—20：00的空闲泊位数进行预测。本文在训练集上进行模型训练，在测试集上检测模型的预测效果，使用同一测试集对不同模型进行验证，比较模型的性能。空闲泊位数预测步骤如图5所示。

图6 模型训练时间对比Fig.6 Comparison of training time of the three models

3.2 数据结果

3.1.1 实验1

使用RTCN模型对10、20、30 min的空闲泊位数进行预测，为了比较算法的性能，分别利用LSTM和GRU神经网络对同一数据进行训练和预测，回溯时间窗口均设置为10，训练次数均为200，损失函数采用均方误差。首先对各个模型的训练时间进行比较，模型训练时间对比结果如图6所示，在进行10、20 min空闲泊位数预测时，RTCN模型的训练时间最短，在进行30 min空闲泊位数预测时，GRU模型的训练时间最短，LSTM的训练时间最长，且远远高于改进RTCN和GRU预测模型，可见LSTM的预测速度较慢，RTCN的训练速度较快。 对工作日与非工作日的空闲泊位数进行预测，计算平均预测误差。预测工作日空闲泊位数的3种模型的预测误差见表1，预测非工作日空闲泊位数的3种模型的预测误差见表2。

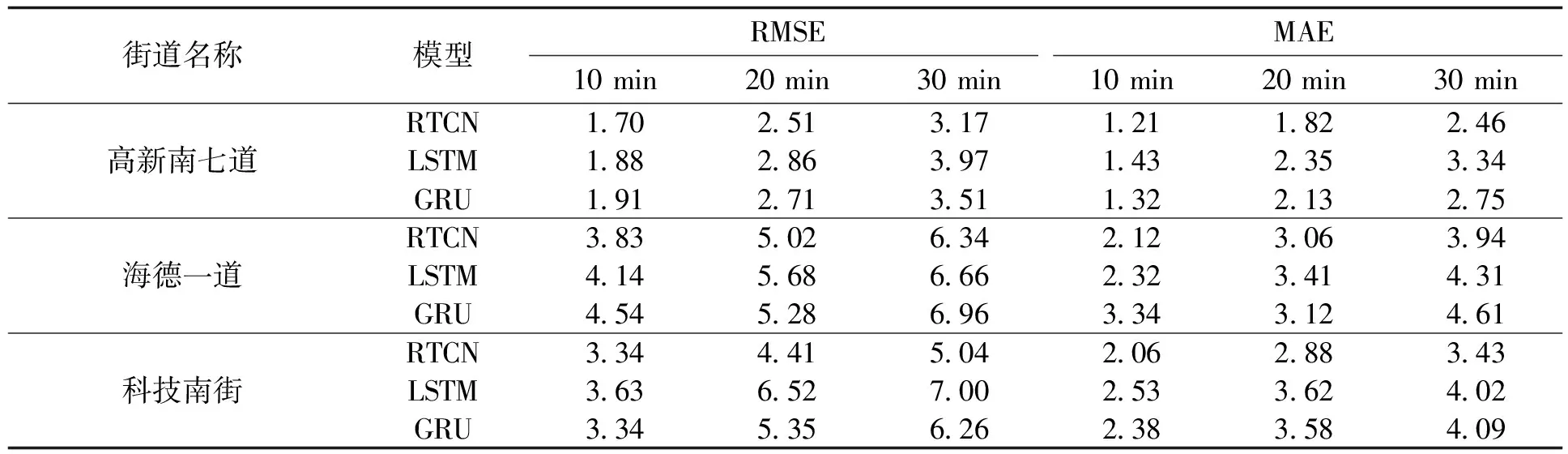
表1 工作日3个模型的预测结果比较Tab.1 Comparison of the prediction results of the three models On weekdays

在工作日，与LSTM预测算法、GRU预测算法相比，RTCN模型的预测性能有明显优势，以高新南七道为例，在预测第10分钟空闲泊位数预测时，在RMSE上RTCN模型比LSTM模型小0.18，比GRU模型小0.21，在MAE上RTCN模型比LSTM模型小0.22，比GRU模型小0.11。在预测20分空闲泊位数预测时，在RMSE上RTCN模型比LSTM模型小0.35，比GRU模型小0.20，在MAE上RTCN模型比LSTM模型小0.53，比GRU模型小0.31。在预测第30分钟空闲泊位数预测时，在RMSE上RTCN模型比LSTM模型小0.80，比GRU模型小0.34，在MAE上RTCN模型比LSTM模型小0.88，比GRU模型小0.29，可见在预测工作日空闲泊位数时，RTCN模型的表现要明显优于LSTM和GRU模型，随着预测时间变长，TCN模型的预测精度提升幅度增大。并且随着预测时间的变长，RTCN、LSTM以及GRU模型的RMSE和MAE均变大，表明3种预测模型的预测精度均随着预测时间的变长而下降。

在非工作日，与LSTM预测算法、GRU预测算法相比，在大部分情况下，RTCN模型的预测性能有优势，以高新南七道为例，在预测第10分钟空闲泊位数预测时，在RMSE上RTCN模型比LSTM模型小0.02，比GRU模型小0.14，在MAE上RTCN模型比LSTM模型小0.25，比GRU模型小0.23。在预测20分空闲泊位数预测时，在RMSE上RTCN模型比LSTM模型小0.50，比GRU模型小0.06，在MAE上RTCN模型比GRU模型小0.06。在预测第30分钟空闲泊位数预测时，在RMSE上RTCN模型比LSTM模型小0.63，比GRU模型小0.23，在MAE上RTCN模型比GRU模型小0.07。在预测非工作日空闲泊位数时，3种模型的RMSE与MAE均随着预测时间的变长而增大，表明模型预测精度随着预测时间的延长而下降。与预测工作日空闲泊位数相比，虽然预测非工作日的空闲泊位数时RTCN模型相较于LSTM和GRU模型预测性能优势下降，但是总体来看RTCN的预测精度高于LSTM和GRU模型。

表2 非工作日3种模型的预测结果比较Tab.2 Comparison of the prediction results of the three modelson weekends

为了进一步分析3种模型在不同空闲泊位状态上的表现，本文按照真实空闲泊位数的大小，将空闲泊位数分为峰值和非峰值2种情况，各个模型的表现如图7所示。

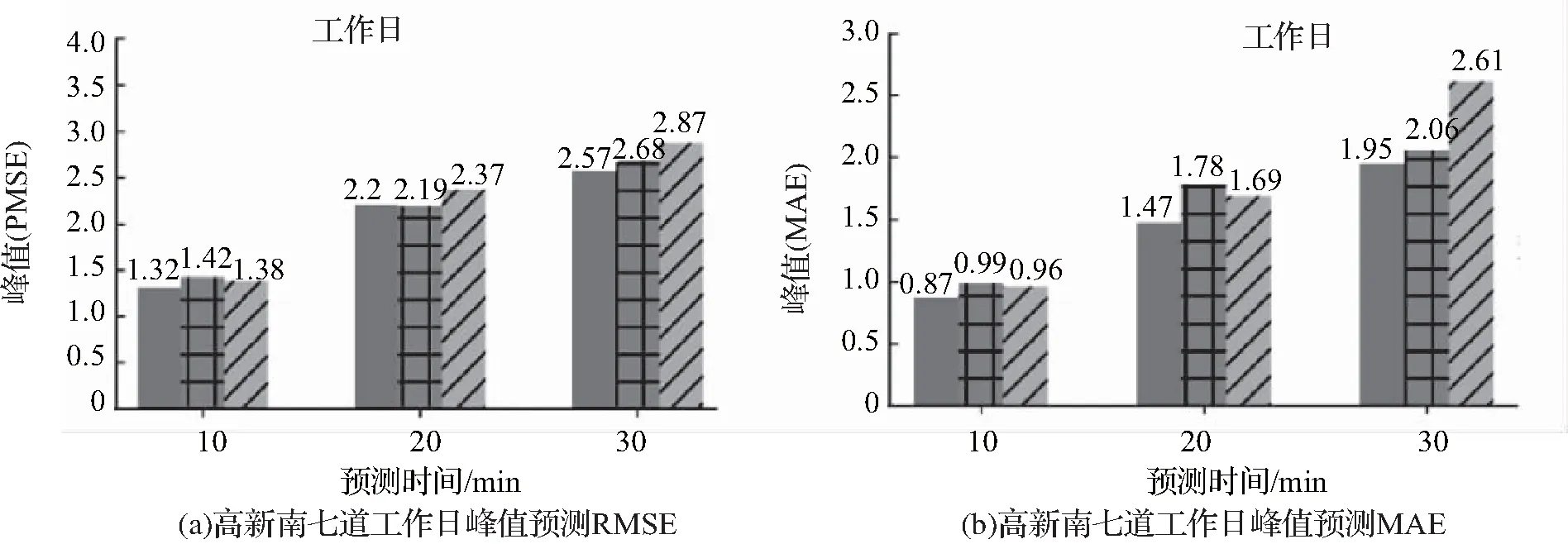
图7 3种模型在各个条件下的表现Fig.7 The performance of the three models under different conditions.

从图7中可以看出，在预测工作日空闲泊位数时，RTCN模型受到空闲泊位数大小的影响较小，始终维持在较好的水平，预测精度高于LSTM和GRU模型，而在预测非工作日空闲泊位数时，在非峰值状态下GRU的预测性能表现更好，在峰值状态下，RTCN模型的表现更好。

3.1.2 实验2

考虑区域占有率的RTCN模型对10、20、30 min的空闲泊位数进行预测，使用考虑区域占有率的RTCN模型针对3个不同预测时间的空闲泊位数进行预测，以高新南七道为例，工作日预测值与真实值对比如图8所示，非工作日预测值与真实值的对比如图9所示。

考虑区域占有率和不考虑区域占有率的模型预测工作日空闲泊位数误差见表3，预测非工作日空闲泊位数误差见表4。

图8 空闲泊位数预测值和真实值对比Fig.8 Comparisonof the predicted value and the real value of the number of free parking spaces on weekdays

图9 非工作日考虑、区域占有率空闲泊位数预测值和真实值对比Fig.9 Comparison of the predicted value and the real value of number of free parking spaces on weekends

表3 工作日两个模型的预测结果比较Tab.3 Comparison of the prediction results of two modelson weekdays

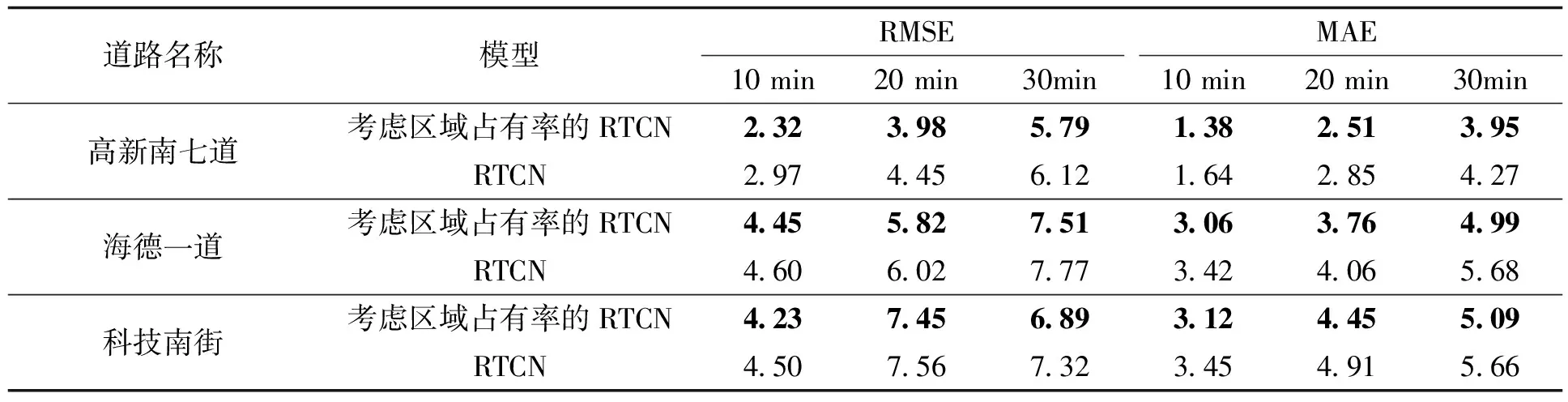
表4 非工作日2种模型的预测结果比较Tab.4 Comparison of the prediction results of the two modelson weekends

在预测工作日空闲泊位数时，将区域占有率引入RTCN模型后，预测精度得到进一步的提升，以高新南七道为例，在预测10 min数据时，考虑区域占有率的RTCN模型的RMSE比RTCN模型低0.15，MAE比RTCN模型低0.20；在预测20 min数据时，考虑区域占有率的RTCN模型的RMSE比RTCN模型低0.46，MAE比RTCN模型低0.37；在预测30 min数据时，考虑区域占有率的RTCN模型的RMSE比RTCN模型低0.19，MAE比RTCN模型低0.23。

在预测非工作日空闲泊位数时，将区域占有率引入RTCN模型后，预测精度得到进一步的提升，以高新南七道为例，在预测10 min数据时，考虑区域占有率的RTCN模型的RMSE比RTCN模型低0.65，MAE比RTCN模型低0.26；在预测20 min数据时，考虑区域占有率的RTCN模型的RMSE比RTCN模型低0.47，MAE比RTCN模型低0.34；在预测30 min数据时，考虑区域占有率的RTCN模型的RMSE比RTCN模型低0.33，MAE比RTCN模型低0.32。

在预测工作日和非工作日空闲泊位数时，随着预测时间的变长，考虑区域占有率的RTCN模型的预测精度下降。

4 总结

通过对空闲泊位数预测问题的研究，本文提出了考虑占有率的基于改进TCN模型的短时空闲泊位数预测方法。与LSTM算法和GRU算法相比，改进TCN预测模型的预测误差更小，训练速度更快，并通过引入区域占有率这一影响因素，建立了考虑占有率的基于改进TCN模型的短时空闲泊位数预测方法，进一步提高了模型的预测精度。

通过对考虑区域占有率的RTCN泊位预测模型研究和实验分析，可以出以下结论：

①TCN模型能够解决空闲泊位数预测的时间特征提取问题；

②RAdam算子与TCN模型结合适用于路内停车空闲泊位的预测，能够提高预测模型的适用性，解决路内停车样本不足的问题；

③增加区域占有率作为RTCN模型的输入能够有效提取空间特征，有助于挖掘空间关联信息，提高预测精度。