反弯点高度比对强梁弱柱钢框架混合试验影响分析
2022-05-08徐天鸿王书琪田石柱
徐天鸿,王书琪,田石柱*,2
(1.苏州科技大学 土木工程学院, 江苏 苏州 2150112.江苏省结构工程重点实验室, 江苏 苏州 215011)
0 引言
我国是世界上地震灾害最为严重的国家之一。近年来我国地震灾害频频发生,地震作用导致结构破坏对经济造成的巨大损失更是不容忽视。由于非线性变形可以耗散大量的动荷载能量,建筑在强震下的安全性是依靠结构构件的延性保证的,因此,对结构在强震下的性能分析主要考察其强度、刚度和延性特征。土木工程师应采取更高效的结构抗震试验方法研究结构抗震性能。基于子结构拟动力试验技术发展而来的抗震混合试验方法是一种经济、有效的结构抗震试验方法[1-3]。
抗震混合试验方法将结构分为两部分:在地震作用下,将结构易出现线性或弱非线性的部分作为计算子结构,易出现强非线性的部分作为试验子结构。计算子结构通过高性能计算机进行模拟,试验子结构在实验室进行物理试验,将两者进行集成协调,实现整体结构的抗震反应分析。
在进行子结构混合试验时,试验子结构与计算子结构之间的复杂边界条件的准确模拟是保证混合试验可行性和精确性的关键。整体结构拆分后,子结构之间的边界协调计算需要不断更新积分算法,保证计算精度,同时利用有限元软件实现对数值子结构的精确模拟[4]。针对试验子结构进行物理实际加载,还原结构拆分后暴露出的自由度,有效实施协同加载,满足子结构间的平衡与协调。在工程实际研究应用中,完全精确模拟界面的水平、竖向、转动三自由度具有较大难度[5]。
2010年,Mosqveda等[6]开发出基于反弯点的子结构混合试验加载方法,将假设反弯点位置选取为二层柱中,克服了控制边界处的刚性轴向和旋转变形的困难,也更容易在实验室实现。2012年,Wang等[7]在反弯点法基础上提出了重叠域的概念,进一步减小试验误差。2015年,孔文江[8]提出基于弹性反弯点的子结构技术,将试验子结构边界选取在柱弹性反弯点位置。2019年,王婧[9]提出复杂边界条件模拟方法,将反弯点边界自由度缩减,进一步简化了反弯点法的边界条件。需要注意的是,在使用此类试验子结构边界加载方法时,反弯点位置的变化对结构加载效果有着直接影响,但是,对于结构受到强震作用直至接近倒塌阶段时,反弯点位置的变化情况及上述试验子结构边界加载方法能否适用,国内外研究较少。OpenSEES是进行框架结构抗震分析的常用软件[10],本文通过建立基于OpenSEES的“强梁弱柱”钢框架模型及开展地震模拟振动台试验,对基于反弯点的子结构混合试验加载方案进行模拟,研究“强梁弱柱”钢框架中反弯点位置在构件损伤时的变化问题。
1 基于反弯点的子结构混合试验加载方法
水平地震作用一般都可以简化为作用于框架节点上的水平力。规则框架在节点水平力作用下结构弯矩如图1所示,其中弯矩为0的点为反弯点。反弯点法已经用于初步设计时,计算层数较少且较为规则的框架在水平地震作用下的内力计算。基于反弯点的子结构混合试验加载方案[7]如图2所示。在子结构拆分位置,具有水平自由度、竖向自由度和转动自由度3种自由度,水平自由度认为是一致的,竖向自由度各结构柱不相同,通过扩展试验单元至二层柱反弯点处,使用反弯点处的水平自由度模拟子结构边界的转动自由度,该扩展区域与数值子结构的第二层区域重叠。利用重叠区域的优点在界面处使用一个水平作动器施加水平位移等效成一层梁柱节点处的转动位移,另一个水平作动器位于节点处,2个水平作动器共同施加节点的水平位移,但试验子结构中试验单元扩展的部分并不在加载过程中模拟结构响应,第二层结构在地震作用下的内力和动力响应完全在数值模拟中实现,扩展部分和数值子结构具有相同的截面,可以有效地传递剪力和弯矩,不仅保证了首层节点处的转动自由度模拟,还确保了节点区域的受力分布。
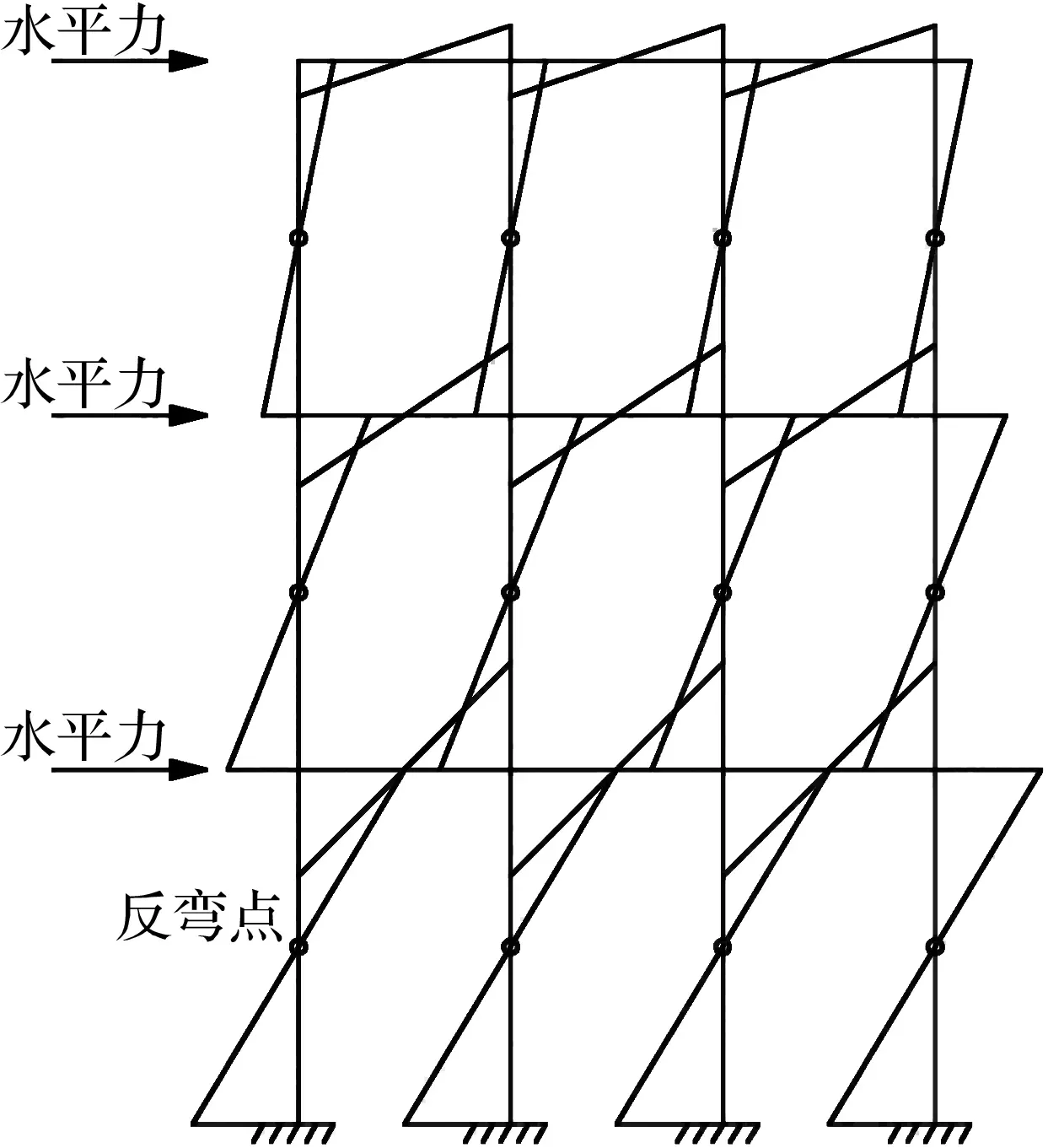
图1 水平力作用下结构弯矩图Fig.1 Structure bending moment diagramunder the action of horizontal seismic force
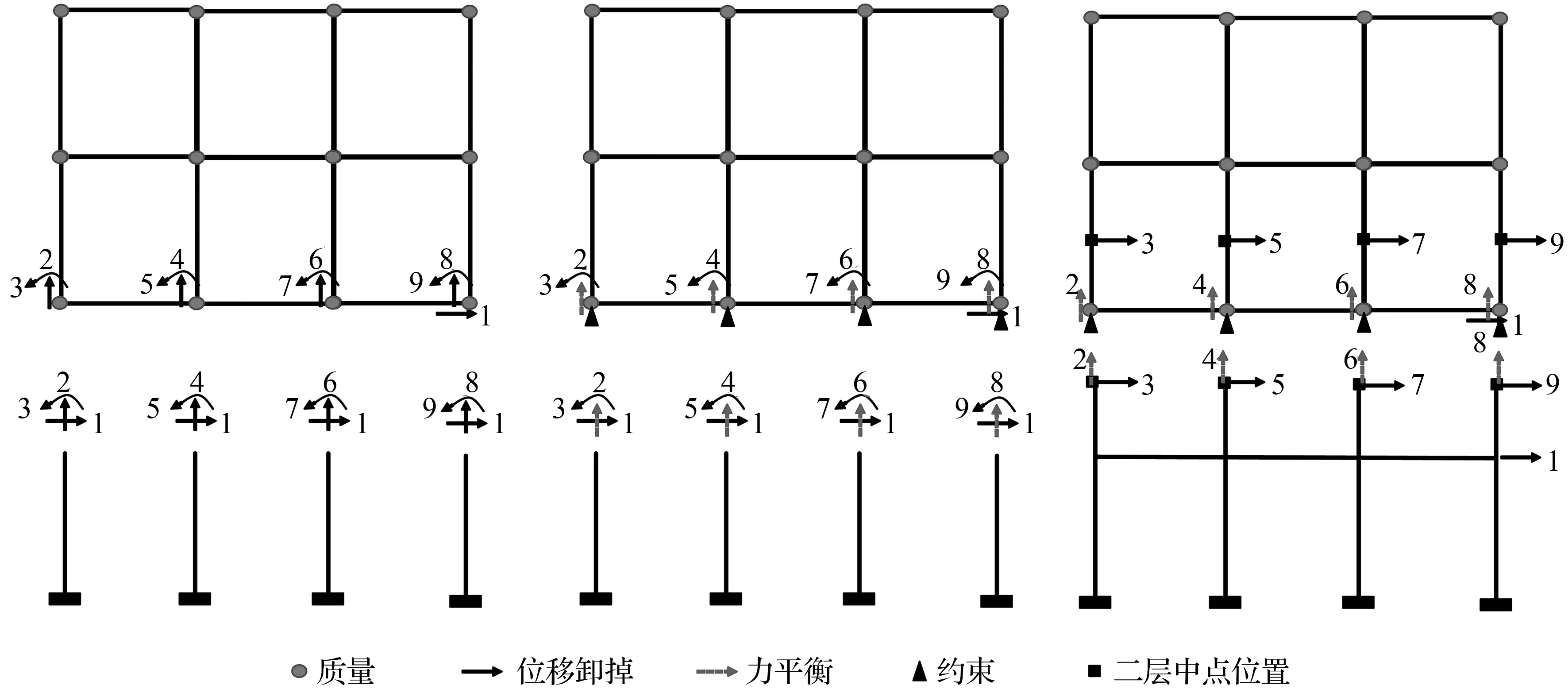
(a) 完全边界条件 (b) 竖向不协调 (c) 放松转动自由度
2 基于OpenSEES的钢框架有限元模拟
2.1 模型和地震波选取
为了进行有限元模拟及地震模拟振动台试验,考虑振动台对模型尺寸和质量的限制,本文设计了一个三层三跨两榀空间钢框架模型。框架模型总高度为1 512.5 mm,总宽度为910.0 mm,层高为500.0 mm,跨度和进深均为300.0 mm。梁柱均采用尺寸为25.0 mm×10.0 mm的Q235扁钢,梁的横截面为25.0 mm×10.0 mm,柱的横截面为10.0 mm×25.0 mm,梁柱线刚度比大于3,每个梁跨中施加1.80 kg的恒荷载。第一层质量为58.10 kg,第二层质量为58.10 kg,第三层质量为54.09 kg,总质量为170.20 kg。钢框架的模型结构如图3所示。
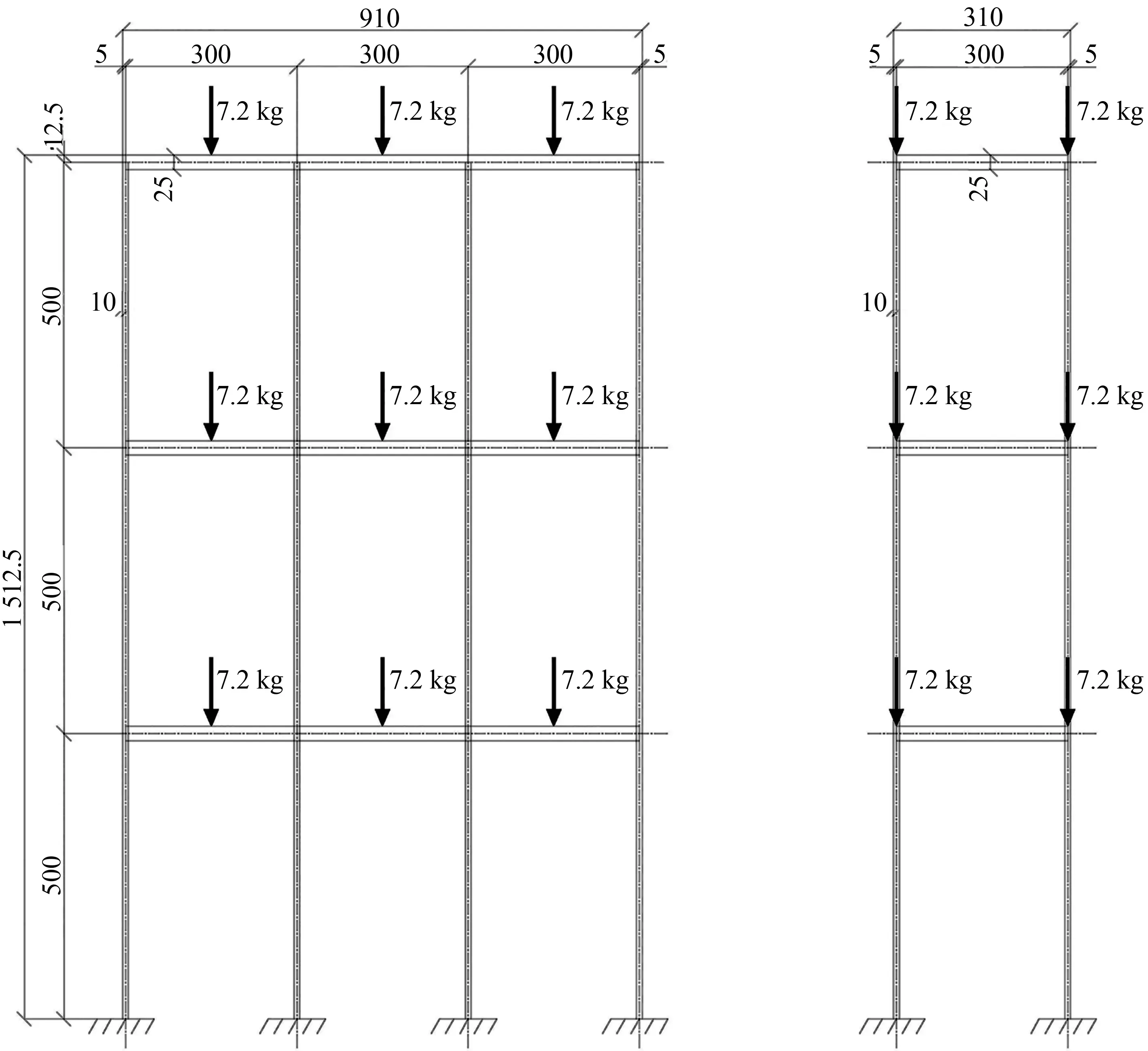
单位:mm
根据建筑结构地震影响系数曲线,本文采用El Centro波及从美国太平洋地震工程研究中心(PEER)强震数据库选取的8条地震波,并将每条地震波调幅为不同峰值加速度的地震波。具体地震波取用见表1。
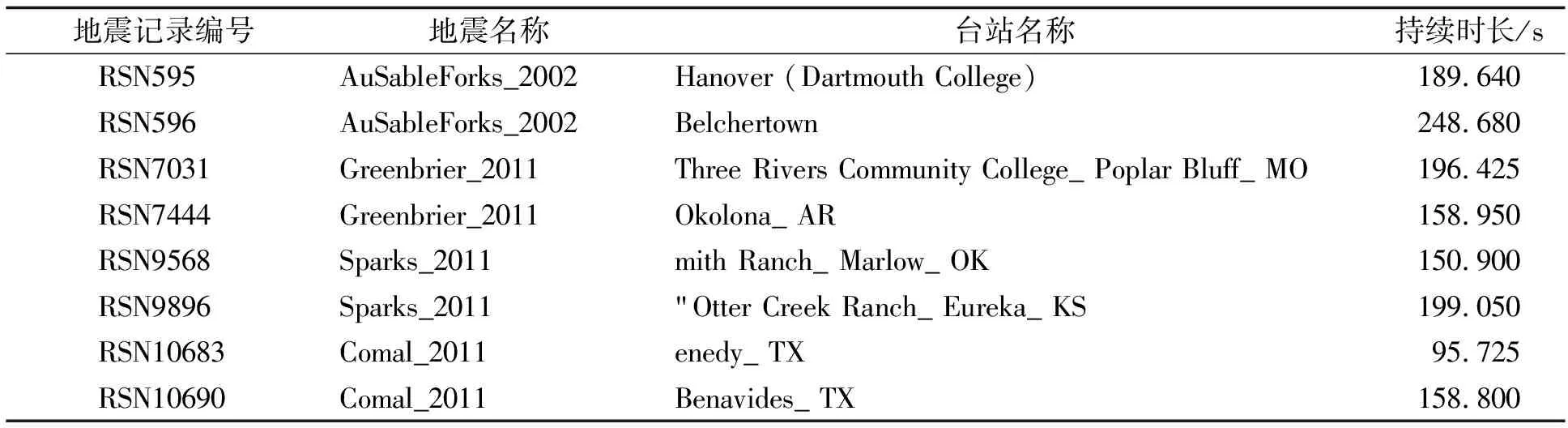
表1 地震波取用表Tab.1 Table for Seismic wave
2.2 模型模拟分析
整个数值模拟采用OpenSEES实现,模型的材料本构均选用OpenSEES自带的强化双折线模型Steel02,材料屈服强度为215 N/mm2。
考虑精度和计算时长的平衡,对截面采用6×15束的纤维截面(fiber section)。采用多尺度建模方法,将底层受地震作用影响较大的梁柱采用具有良好代数精度的Two-Point Gauss-Dadau分布塑性铰单元(force beam column element),二层、三层梁柱采用分布塑性梁柱单元(nonlinear beam column element)。运动方程中阻尼矩阵C采用Rayleigh阻尼,即
(1)

对模型输入地面加速度进行动力时程分析,得到框架柱底高斯点的弯矩和曲率,绘制框架柱弯矩曲率曲线如图4所示,图中给出EL Centro波下不同地震峰值加速度的弯矩曲率曲线。

(a)边柱

图5 割线刚度破坏参数定义示意图Fig.5 Parameter definition ofstiffness degradation
为了研究构件在强震作用下进入强非线性状态时反弯点位置的变化情况,选取首先进入强非线性的底层柱作为研究对象,所得到的结论对其他构件也适用。采用反弯点高度比y0和杜修力等[11]提出的以割线刚度比为破坏参数的构件损伤指标D,建立反弯点位置的变化情况和构件损伤程度的关系,损伤指标采用构件的弯矩曲率进行计算。
定义破坏参数的表达式如式(2)所示:
(2)
式中:Km是构件的初始弹性刚度;K0是构件在最大变形处对应的割线刚度。割线刚度破坏参数定义示意图如图5所示。
当η=0时结构构件完好无损。现假定构件的变形处在负刚度段,且强度丧失到可以认为是无承载能力时,则构件将最终破坏。一般定义对应的强度为极限强度的80%。定义此时相应的割线刚度为Kf,相应的破坏参数的极限值为
(3)
因此,构件的损伤指标定义如式(4)所示,D=0时构件完好无损,D=1时构件失效破坏。
(4)
框架柱损伤指标如图6所示。从图6中可以看出,随着地震动峰值加速度的增大,构件损伤程度逐渐增大,最终达到倒塌。

(a)边柱
输出模型计算的柱端弯矩,反弯点高度比y0计算公式为
(5)
式中:Mbi为第i层柱底部弯矩;Mai为第i层柱顶部弯矩。
由于地震作用大小和方向不断发生随机变化,因此水平荷载和竖向荷载组合形成的柱端弯矩的大小和方向也相应发生变化,结构柱的反弯点高度比发生波动。当柱端弯矩较大时,结构竖向荷载作用下的柱端弯矩占比较小,可忽略不计。基于此,本文给出了柱底最大弯矩处的反弯点高度比y0与构件损伤指标D的关系图,不同地震波下反弯点高度比与构件损伤指标的关系如图7所示。在实际结构中,由于基础对底层柱柱底的约束不变且强于底层柱上部约束,所以底层柱反弯点一般在柱子的2/3高度处。本文所采用的缩尺模型中柱底约束与柱顶约束相近,底层柱反弯点位置在柱中附近。从图7可以看出:在构件不发生损伤时,反弯点高度比大于0.5,其中边柱为0.518,中柱为0.506;在强震作用下,构件损伤程度不断增加,反弯点高度比逐渐减小,并趋近0.5;与边柱相比,中柱更加稳定,波动较小。

(a)边柱
为了研究将柱中视为反弯点位置是否具有较大误差,定义反弯点高度比与柱中位置的差为试验加载误差,试验加载误差与地震动峰值加速度的关系如图8所示。从图8中可以看出:边柱的试验加载误差比中柱大,但均没超过5%,其中边柱误差小于4%,中柱误差小于1%。

(a)边柱
3 地震模拟振动台试验

图9 试验结构的IDA曲线Fig.9 Change curve of IDA
对图3的结构进行地震模拟振动台试验,以验证结构柱反弯点高度比的变化。采用OpenSEES对结构的动力特性分析,结构模态参数见表2。

表2 结构模态参数Tab.2 Model parameters
振动台试验已经在文献[12]中详细描述。恒荷载采用配重块加载,地震波根据我国抗震设计规范要求选取,分别为El Centro波(N-S)、宁河(S-N)、Taft(北偏东21°)。由于地震台尺寸及性能的限制,地震动峰值加速度不能超过1.4 g,结构仅进入弹塑性状态。试验测量了结构的层间位移,试验结构的IDA曲线如图9所示,图中给出结构基于IDA方法的损伤指标[13]。从图中可以看出,结构已进入弹塑性状态。
在振动台试验中,通过粘贴应变片得到结构底层柱的柱端应变,采用与式(5)类似的计算方式得到底层柱的反弯点高度比。根据结构的IDA分析,随着地震峰值加速度的增加,结构的损伤程度也随之增加。
图10所示为反弯点高度比与地震动峰值加速度的关系。从图中可以看出:边柱受力比中柱复杂,中柱试验结果更稳定;柱反弯点位置保持在柱中附近,且有一定的下降趋势。图11所示为试验加载误差与地震动峰值加速度的关系。从图中可以看出定义的试验加载误差小于1%。试验结果表明:①底层柱反弯点位置在柱中附近,试验加载误差较小;②构件进入损伤阶段,强度退化时,反弯点位置逐渐下降。试验结果与OpenSEES分析结果相符,验证了OpenSEES分析结果的可靠性。

(a)边柱

(a)边柱
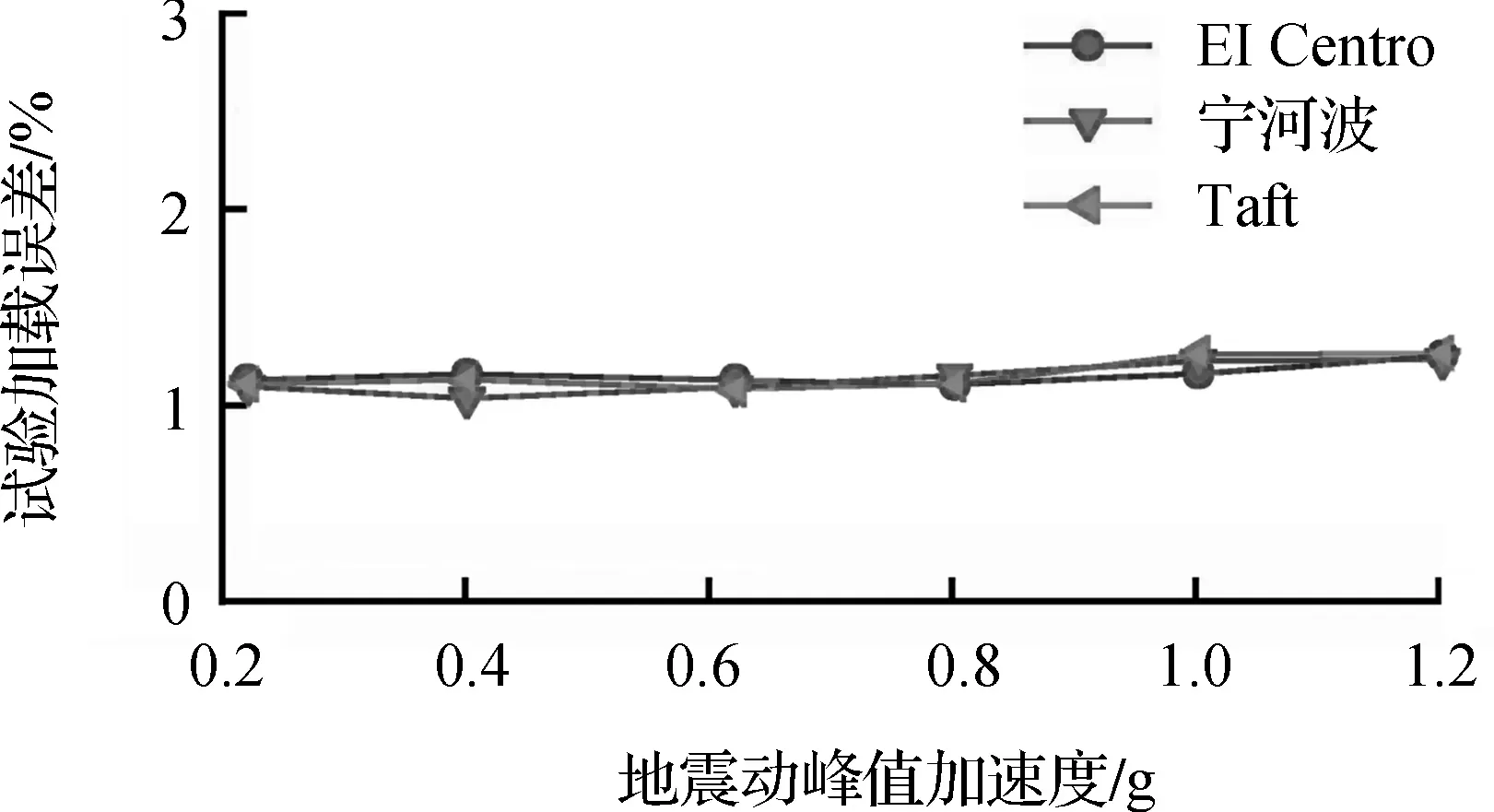
(b)中柱
4 结论
“强柱弱梁” 是结构抗震设计的要求,《建筑抗震设计规范》(GB50011—2010)中采用柱端弯矩增大系数来实现这一设计目标,但是在实际结构设计中,考虑楼板影响、梁端按裂缝宽度控制配筋等情况,“强梁弱柱”的破坏模式难以避免,所以对于“强梁弱柱”结构的抗震混合试验方法的研究有其特定意义[14]。
由于“强梁弱柱”结构底层柱受地震荷载作用最大,本文选取结构的底层边柱和中柱,通过选择9条地震波,基于OpenSEES有限元软件数值模拟和地震模拟振动台试验验证,研究了结构强震作用下反弯点高度比的变化以及基于反弯点的试验子结构加载边界方法的可靠性,得出以下结论:
① 在弹性阶段,由于柱顶梁柱节点处结构竖向荷载的弯曲变形及二阶效应,柱底弯矩较柱顶弯矩稍大,柱反弯点位置在柱中上方;随着构件进入塑性阶段,损伤程度的增大,柱端产生塑性铰,弯矩保持不变,且柱顶竖向荷载形成的弯矩占比减小,反弯点位置下降,并在柱中位置保持稳定。
② 本文采用的“强梁弱柱”结构在强震作用下,边柱反弯点位置变化较中柱大,推测是由于边柱柱顶弯曲变形影响了弹性反弯点位置,将在后面的工作中继续研究。由于混合试验中加载边界难以移动,因此若将柱中作为试验子结构的加载边界,边柱的试验加载误差小于4%,中柱的试验加载误差小于1%,总体误差较小,均符合试验精度要求。
③ 基于反弯点的子结构混合试验加载方案是一种简便、有效的混合试验加载方式,对于“强梁弱柱”结构,若混合试验只进行弹性阶段或弱非线性阶段,加载边界可采用有限元弹性分析确定弹性反弯点位置;若需要进行强非线性的混合试验,可将加载边界取在结构柱中位置。
