地震作用下饱和软土场地地下结构动力参数敏感性模拟分析
2022-05-08程学磊李文东海然刘彦何鲜峰夏锦红
程学磊,李文东,海然,刘彦,何鲜峰,夏锦红
(1. 中原工学院 建筑工程学院, 河南 郑州 450007; 2.黄河水利委员会黄河水利科学研究院 工程力学研究所, 河南 郑州 450003;3.大连海事大学 交通运输工程学院, 辽宁 大连 116026; 4.新乡学院 土木工程与建筑学院, 河南 新乡 453003)
0 引言
现行软土场地地铁车站结构体系抗震规范设计方面与可液化砂土地基场地相比还较为粗泛,仅给出了若干定性、笼统的规定,尚缺乏更为深入和系统的研究。考虑软弱场地影响的地铁车站结构动力体系地震响应对于加深地铁车站结构抗震认识和促进岩土地震工程发展均具有重要的理论价值和实践意义[1-3]。
近年来,国内外学者在软土场地地铁地下结构抗震方面进行了诸多相关研究。Pitilakis等[4]基于动力总应力数值方法,参数化系统研究了地下结构与地表结构体系在水平地震激励下的复杂动力响应。庄海洋等[5]还基于动力总应力方法,考虑土体与混凝土非线性以及土结接触非线性,研究了地铁车站在规范规定的不同场地类别条件下地下结构层间位移和位移角反应特征以及结构关键部位的应力反应特征。夏晨等[6]基于动力总应力方法,通过建立合理计算模型研究了不同结构刚度、接触面摩擦系数以及地震波等条件下地铁车站的最大层间位移变形。唐小微等[7]基于动力总应力方法,建立软土场地箱型双层预应力大跨度地铁车站体系非线性相互作用有限元模型,分析了震害发生时大跨度预应力地铁车站结构的破坏过程、破坏形式和抗震薄弱位置。Zhuang等[8]基于动力总应力有限元方法,提出了土-结静动力耦合接触模型,其中土体采用改进的黏塑性本构模拟土体强非线性特征,对软土场地地铁车站地震损伤情况进行了评估。进一步地,崔春义等[9]采用饱和两相介质动力分析方法,分析了软基场地中地铁车站结构动力响应特性和灾变机理。在已有软土场地地铁地下结构研究专题中,软土地基土性参数对地铁地下结构地震动力响应敏感性分析还有待进一步研究。
本文将结合已有国内外相关研究成果的特点和局限性展开,基于有限元开源程序平台OpenSEES,采用完全耦合饱和两相介质有效应力动力求解方法,建立饱和软土场地-地铁地下结构非线性动力相互作用体系数值计算模型,其中场地土体采用多屈服面动力弹塑性本构模型,地铁车站结构采用能考虑截面型式及配筋率的纤维截面弹塑性模型,由各土性因素参数(六因素、三水平)对饱和软土场地中地铁车站结构动力响应各指标进行极差、方差和线性回归分析的参数敏感性分析。
1 数值计算模型
OpenSEES(open system for earthquake engineering simulation)是一个在土木工程领域广泛应用的有限元计算平台,可用于岩土及结构工程非线性静动力分析,OpenSEES计算流程如图1所示。本文数值算例以饱和软土场地单层双跨地铁车站为背景(1995年日本阪神地震大开车站坍塌段结构型式),地铁车站结构横截面尺寸如图2所示。其中,结构埋深11.00 m,横截面尺寸:宽为17.00 m,高为7.17 m,中柱间距为3.50 m。所建立的软土夹层场地地铁车站结构动力相互作用体系有限元计算模型如图3所示,场地尺寸为170.00 m×30.00 m。场地土体采用quadUP水土耦合单元模拟,土层计算参数结合室内实验值并参考OpenSEES黏土本构推荐值选取[10],软质黏土本构参数取值见表1。

图1 OpenSEES计算流程Fig. 1 Calculation flow chart of OpenSEES

图2 地铁车站结构横截面尺寸Fig. 2 Cross section ofsubway station structure

图3 有限元计算模型Fig. 3 Finite element model of calculation

表1 软质黏土本构参数取值Tab.1 Model parameters of soft clay
地铁地下结构采用纤维截面单元考虑其非线性动力性能,纤维截面示意图如图4所示。具体地,结构混凝土采用Concrete02本构模型(修正 Kent-Park混凝土模型[11-12]),钢筋混泥土本构模型如图5所示。混凝土应力-应变关系如图5(a)所示,图5(a)中应力σ、应变ε、弹性模量E等参数取值参考文献[11],混凝土密度为2 500 kg/m3;钢筋采用Steel02动力等向硬化双线性材料模型[13]。钢筋应力-应变关系如图5(b)所示,其中钢筋弹性模量为200 GPa,屈服强度为400 MPa。

图4 纤维截面示意图Fig. 4 Schematics of fiber cross section
本文采用的饱和两相介质矩阵数值方程为[14]

(1)
(2)
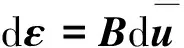
黏土采用多屈服面运动塑性本构,黏土多屈服面模型屈服面方程为
(3)

黏土多屈服面塑性本构采用偏量随动硬化定律,屈服面运动方向张量定义为
(4)
式中,sT为二阶偏应力张量,表示屈服面fm+1和fm交点的偏应力张量;αm和αm+1分别为屈服面fm和fm+1中心。
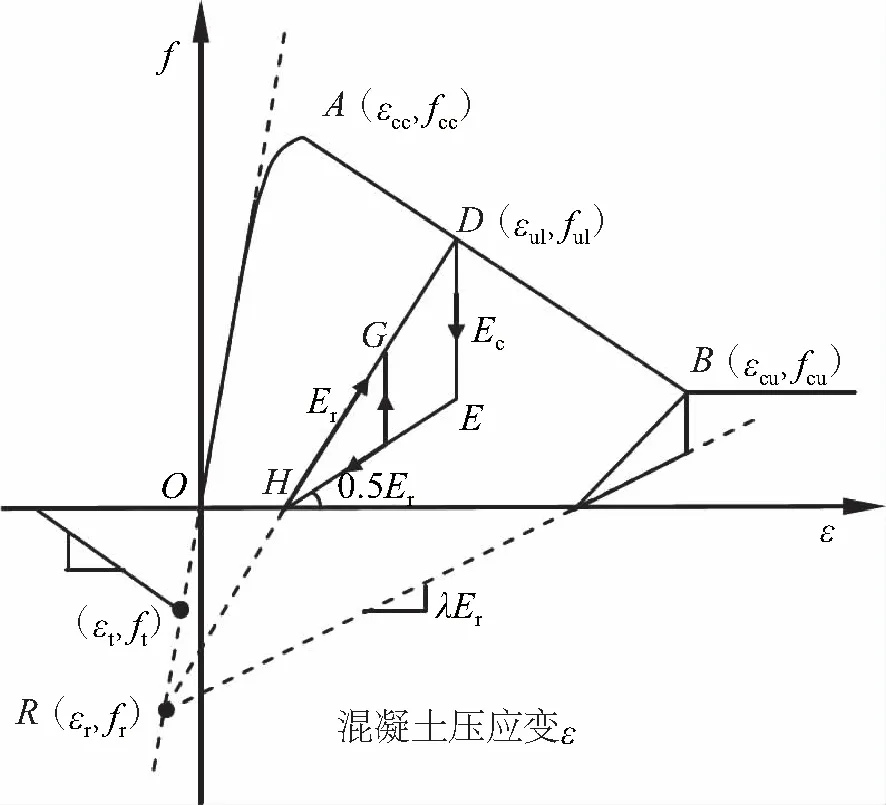
(a) 混凝土压应力f-压应变ε曲线

(b) 钢筋应力f-应变ε曲线
数值模型具体采用Rayleigh阻尼模拟能量的耗散效应,具体选取5%阻尼比。场地底部和两侧设定为不排水边界,地表为排水边界。为更好模拟地基半无限空间效应,选取模型尺寸为结构宽度10倍,且两侧设定为捆绑边界。动力计算中采用HHT逐步时间积分方法求解,该方法可以考虑能量消散和二阶精度。
在进行动力分析之前,先进行初始地应力平衡(弹性-塑性阶段),之后由基底刚性边界水平输入持续时间为30 s的Kobe地震波,波形和对应傅里叶谱如图6所示,该地震波低频成分较为丰富,特征频率为1.5 Hz(对应特征周期0.67 s),根据《建筑抗震设计规范》(GB 50011—2010),一般土与软弱土场地特征周期为0.60~0.80 s,因此Kobe地震波适用于软土场地。所有数值计算结果均通过自编MATLAB接口程序实现提取和处理。

(a) 地震动时程

(b) 傅里叶谱
2 饱和软基中地铁地下结构地震动力响应指标参数敏感性分析
2.1 动力评价指标的确定
地下结构动内力峰值呈现对称分布,并主要集中在板柱节点位置[15]。为了便于分析,选取如图7所示车站结构板柱节点位置作为结构关键截面。图8所示为不同地震作用下各关键截面动内力峰值变异系数情况。由图8可见,相较于动轴力而言,地震动强度变化(0.05g、0.10g、0.20g和0.30g)对车站结构动弯矩和动剪力影响更为显著。由于地下结构为对称结构,仅在重力作用下P7和P8位置主要承受压力,因此剪力和弯矩理论上为0。其次,中柱截面显著小于其他位置剪力墙结构,因此在地震作用下导致中柱的动剪力和动弯矩峰值变化较大。按照各关键截面动内力峰值变异系数大小进行排序,动轴力峰值变异系数前2个关键截面位置为顶板两端(P11位置、P14位置),动剪力和动弯矩峰值的前2个显著关键截面位置均为中柱上、下端部(P7、P8位置),进而将上述截面位置作为后续分析中的最不利截面位置。
具体选取底板中端上抬量、底板中端下5 m处特征点F1处动孔压比峰值和结构动轴力峰值(P14位置)、结构动剪力峰值(P8位置)及结构动弯矩峰值(P8位置)为地铁车站结构动力响应典型指标,进而针对软基土性参数所引起的动力响应指标变化进行参数敏感性分析[9]。
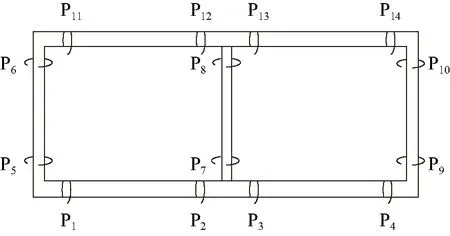
图7 地铁车站结构关键截面受力部位示意图Fig.7 Schematic diagram of key parts of dynamic force of subway station structure

图8 各地震动强度作用下关键截面动内力峰值变异系数Fig. 8 CV for dynamic internal forces of typical sections with different earthquakes
2.2 参数敏感性分析
由于土体的非均质性及复杂多变性,本文拟采用L18(36)正交表安排饱和软土本构参数密度、参考剪切模量、参考体积模量、黏聚力、渗透系数及孔隙率共6个土性参数进行“六因素、三水平”18组数值试验分析。各因素变化幅度为±5%,具体为减少5%(记为-5%,水平1),不变(记为0,水平2),增加5%(记为5%,水平3)。因此,按照各因素变化幅度,密度3个水平值分别为1.62、1.70、1.79×103kg/m3(水平1、水平2、水平3,下同);参考剪切模量3个水平值分别为1.62、1.70、1.79×104kPa;参考体积模量3个水平值分别为7.51、7.90、8.30×104kPa;黏聚力3个水平值分别为17.1,18.0,18.9 kPa;渗透系数3个水平值分别为0.95、1.00、1.05×10-7m/s;孔隙率3个水平值分别为0.57、0.60、0.63。正交试验设计方案见表2,对应各工况下典型指标动力响应值见表3。

表2 正交试验设计方案(六因素、三水平)Tab.2 Orthogonal experimental design (six factors and three levels)

表3 正交试验设计方案中各工况动力响应值Tab.3 Results of dynamic responses of various conditions based on orthogonal design
2.2.1 极差分析
对应软基土性参数因素变化的结构动力响应指标极差如图9所示。
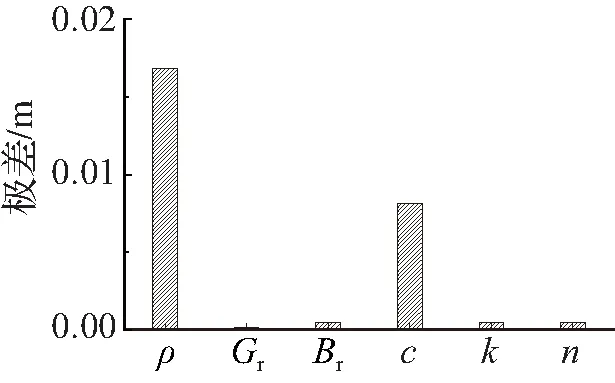
(b) 底板中点上抬量

(c) P14动轴力
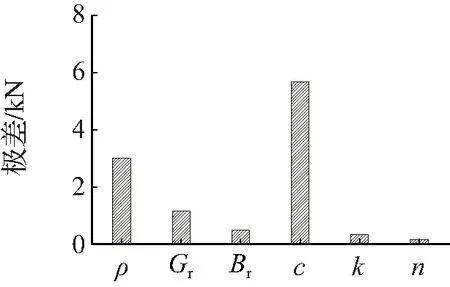
(d) P14动剪力

(e) P14动弯矩
由图9可见,各因素对特征点F1动孔压比峰值的指标敏感性由大到小依次为参考剪切模量,密度,黏聚力,参考体积模量,渗透系数、孔隙率;各因素对底板中点上抬量的指标敏感性由大到小依次为密度,黏聚力,参考体积模量、渗透系数、孔隙率,参考剪切模量;各因素对P14位置动轴力峰值的指标敏感性由大到小依次为密度,黏聚力,参考体积模量,参考剪切模量、渗透系数、孔隙率;各因素对P8位置动剪力峰值的指标敏感性由大到小依次为黏聚力、密度、参考参考剪切模量、参考体积模量、渗透系数、孔隙率;各因素对P8位置动弯矩峰值的指标敏感性由大到小依次为黏聚力,密度,参考剪切模量,参考体积模量,渗透系数、孔隙率。
综上所述,对饱和软基中地铁车站结构地震动力响应指标敏感性最为显著的土性参数为密度和黏聚力,且敏感性明显高于其他土性参数,其次为参考剪切模量,其对特征点动孔压比峰值敏感性最大,其他参数的敏感性相对较小。特别地,渗透系数和孔隙率参数变化对结构动力响应指标极差均较小,说明渗透系数和孔隙率为6个土性参数中最不敏感的因素参数。
2.2.2 方差分析
正交试验设计方案中各工况动力响应值见表4。从表4中可以看出:饱和软土密度和黏聚力的变化对结构底板上抬、特征截面动内力响应影响高度显著;剪切模量变化对特征截面动剪力和动弯矩峰值影响高度显著,对结构底板上抬较为显著;体积模量变化对动轴力峰值影响高度显著,对动剪力和动弯矩峰值影响较为显著;渗透系数和孔隙率变化对响应指标影响均不显著。

表4 正交试验设计方案中各工况动力响应值Tab.4 Results of dynamic responses of subway station based on orthogonal design
2.2.3 回归分析
① 动孔压比峰值多元回归分析
对18组特征点动孔压比峰值正交数值试验数据进行多元线性回归,线性方程为
y=0.227-0.013x1+ 0.016x2-0.002x3+0.012x4-0.009x5+ 0.009x6,
(5)
式中:y为特征点动孔压比峰值;x1为饱和软土密度;x2位参考剪切模量;x3为参考体积模量;x4为黏聚力;x5为渗透系数;x6为孔隙率。
对回归方程进行显著性检验,求得P值水平为P=[0,0.085,0.035,0.767,0.105,0.220,0.220],不难看出,在显著性水平为0.05的情形下,常数项、参考剪切模量与特征点动孔压比峰值存在线性关系,其他因素试验值与回归方程拟合程度一般,回归效果不显著,因此不能引入方程。于是,方程可改写为
y=0.227+0.016x。
(6)
② 底板中点上抬量多元回归分析
同样,对18组结构底板中点上抬量正交数值试验数据进行多元线性回归,得到如下线性方程:
y=0.036+0.008x1+0.000x2+0.000x3-0.004x4+0.000x5+0.000x6。
(7)
对回归方程进行显著性检验,求得P值水平为P=[0.000,0.000,0.259,0.644,0.000,0.816,0.490]。不难看出,在显著性水平为0.05的情形下,常数项、密度和黏聚力与特征点结构底板中点上抬量存在线性关系,其他因素试验值与回归方程拟合程度一般,回归效果不显著,因此不能引入方程。于是,方程可改写为
y=0.036+0.008x1-0.004x4。
(8)
③ P14位置动轴力多元回归分析
对18组P14位置动轴力峰值进行多元线性回归,得到如下线性方程:
y=1 248.667+50.667x1+0.167x2+5.167x3+9.917x4-0.333x5+0.333x6。
(9)
对回归方程进行显著性检验,求得P值水平为P=[0.000,0.000,0.772,0.000,0.000,0.565,0.565]。不难看出,在显著性水平为0.05的情形下,常数项、密度、参考体积模量和黏聚力与特征截面P14位置处动轴力存在线性关系,其他因素试验值与回归方程拟合程度一般,回归效果不显著,因此不能引入方程,于是
(6)You flexible spending account form was not signed.
y=1 248.667+50.667x1+5.167x3+9.917x4。
(10)
④ P8位置动剪力多元回归分析
对18组P8位置动剪力峰值进行多元线性回归,得到如下线性方程
y=62.056+1.500x1-0.583x2-0.083x3+2.833x4-0.167x5+0.083x6。
(11)
对回归方程进行显著性检验,求得P值水平为P=[0.000,0.000,0.003,0.603,0.000,0.307,0.603]。不难看出,在显著性水平为0.05的情形下,常数项、密度、参考剪切模量和黏聚力与特征截面P8位置处动剪力存在线性关系,其他因素试验值与回归方程拟合程度一般,回归效果不显著,因此不能引入方程,于是
y=62.056+1.500x1-0.583x2+2.833x4。
(12)
⑤ P8位置动弯矩多元回归分析
对18组P8位置动弯矩峰值进行多元线性回归,得到如下线性方程:
y=222.222+4.750x1-1.750x2-0.500x3+10.500x4-0.250x5+0.167x6。
(13)
对回归方程进行显著性检验,求得P值水平为P=[0.000,0.000,0.000,0.019,0.000,0.196,0.379]。不难看出,在显著性水平为0.05的情形下,常数项、密度、参考剪切模量、参考体积模量和黏聚力与特征截面P8位置处动剪力存在线性关系,其他因素试验值与回归方程拟合程度一般,回归效果不显著,因此不能引入方程。于是
y=222.222+4.750x1-1.750x2-0.500x3+10.500x4。
(14)
3 结论
本文基于u-p格式Biot动力固结方程和饱和两相介质有效应力动力求解方法,建立了饱和软土场地-地铁车站结构相互作用体系有效应力耦合动力分析数值模型,围绕饱和软土地基中地铁车站结构地震动力响应分析指标,进一步通过对各土性参数因素变化对强震作用引起的软基结构动力响应各指标敏感度进行了综合分析。计算与分析结果表明:
① 由各土性因素参数对软基中地铁车站结构动力响应各指标的极差分析情况可知:对饱和软基中地铁车站结构地震动力响应指标敏感性最为显著的土性参数为密度和黏聚力,且敏感性明显高于其他土性参数;其次为参考剪切模量,其对特征点动孔压比峰值敏感性最大;其他参数的敏感性相对较小。特别地,渗透系数和孔隙率参数变化对结构动力响应指标极差均较小,说明渗透系数和孔隙率为6个土性参数中最不敏感的因素参数。
② 由各土性因素参数对软基中地铁车站结构动力响应各指标的方差分析情况可知:饱和软土密度和黏聚力的变化对结构底板上抬、特征截面动内力响应影响高度显著;剪切模量变化对特征截面动剪力和动弯矩峰值影响高度显著,对结构底板上抬较为显著;体积模量变化对动轴力峰值影响高度显著,对动剪力和动弯矩峰值影响较为显著;渗透系数和孔隙率变化对响应指标影响均不显著。
③ 由各土性因素参数对软基中地铁车站结构动力响应各指标的线性回归情况可知:在显著性水平为0.05的情形下,常数项、参考剪切模量与特征点动孔压比峰值存在线性关系;常数项、密度和黏聚力与特征点结构底板中点上抬量存在线性关系,常数项、密度、参考体积模量和黏聚力与特征截面P14位置处动轴力存在线性关系,常数项、密度、参考剪切模量和黏聚力与特征截面P8位置处动剪力存在线性关系,常数项、密度、参考剪切模量、参考体积模量和黏聚力与特征截面P8位置处动剪力存在线性关系。
