半实物射频仿真的误差联合概率密度函数分析

唐 波, 刘乃文, 马 静, 郭琨毅, 盛新庆

(1. 北京科技大学计算机与通信工程学院, 北京 100083; 2. 北京仿真中心航天系统仿真重点实验室,北京 100854; 3. 北京理工大学集成电路与电子学院射频技术与软件研究所, 北京 100081)

0 引 言

半实物射频仿真是雷达导引头系统研发过程中常用的一种测试方法,是介于外场试验与全数字仿真之间的一种仿真技术,既在一定程度上克服了外场试验所需费用较大的问题,又通过实物在回路而使仿真保持了相当高的真实度。现在世界上的一些主要国家和大型研发公司,都建立有半实物射频仿真实验室。例如英国的马可尼公司、美国的埃格林空军基地导弹仿真实验室、陆军高级仿真中心等。我国也在相关科研院所建立了半实物射频仿真实验室。半实物射频仿真微波暗室中,多个辐射天线单元整齐排列,构成天线阵列墙。微波暗室的另一端是一转台,可以将待测雷达导引头系统置于其上。为了仿真某一方向过来的点目标回波,可以使用在方向上包围该点目标的相邻的3个辐射单元。这3个辐射单元构成了一个三元组。通过调整三元组中每个辐射单元的馈电幅度,可以模拟该点目标在三元组构成的三角形内不同方向的回波,从而可以快速地仿真点目标在运动轨迹上每个位置处的散射回波。三元组仿真的目标方位位置可以由重心公式给出。

对于半实物射频仿真,相关的研究文献目前主要关注以下几个方面:仿真误差分析,近场误差与近场修正,仿真对象的扩展,仿真误差的抑制等。例如,文献[4]研究了仿真的实时控制技术,文献[5]研究了宽带雷达的射频仿真问题。由于器件以及模型的非理想性,射频仿真不可避免地存在误差。文献[7]使用统计方法对射频仿真系统的误差以及可靠性进行了分析。文献[8-9]建立了射频仿真误差模型。文献[10-11]研究了近场效应、近场误差的产生以及近场修正算法。文献[12]研究了对多个散射中心进行半实物射频仿真的问题和误差分析。文献[13]提出使用分集的方法来抑制仿真误差。文献[14-15]研究了幅度相位误差对仿真误差的影响。文献[16]研究了天线方向图、转台误差等对仿真误差的影响。文献[17]从不同象限的天线接收信号强度着手对三元组近场误差进行了修正。文献[18]研究了耦合对半实物射频仿真角度误差的影响。文献[19]研究了近场效应对仿真精度的影响。文献[20]给出了比幅单脉冲导引头仿真的近场修正表格。上述对半实物射频仿真误差的研究多从方位角误差和俯仰角误差分别进行研究,而没有考虑到这两个不同角度域上误差的相关性;或仅考虑二维角度误差幅值的均方根,而没有考虑角度误差的方向性分布。

随着雷达技术的精进,对其半实物射频仿真误差的评估需要更精确地进行。仿真角度误差是评估半实物射频仿真系统的一个重要指标。因此,为了对仿真角度误差进行更精确地描述,需要对其在二维角度域上的联合概率密度函数(probability density function, PDF)进行研究。

因此,本文将从常见的馈电幅度误差着手,研究其导致的仿真角度误差在二维角度域上的联合PDF分布。

1 三元组仿真的数学坐标系

半实物射频仿真通过3个相邻的构成正三角形的3个辐射单元,按照一定的幅度比例对3个单元进行馈电,其在空间中叠加生成的总的辐射场在转台处的能流密度或相位梯度沿着真实点目标的视线方向,从而仿真该点目标的散射回波。为了研究方便,建立如下坐标系:以转台位置处为坐标原点,转台与三元组的中心点的连线为轴,三元组的底边与轴平行,三元组所在平面平行于面。

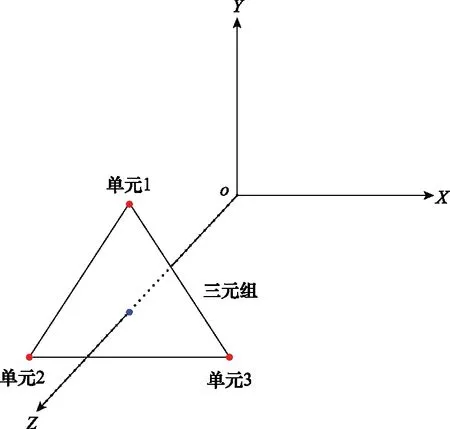
图1 三元组仿真数学坐标系Fig.1 Coordinates system of three-unit-array simulation

三元组3个单元的坐标为(,,),=1,2,3,在球坐标系下表示为(,,),=1,2,3。将直角坐标(,,)对距离归一化,得

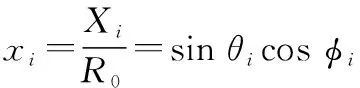
(1)

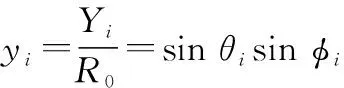
(2)

同样,可得目标的关于距离归一化的直角坐标为

=sincos

(3)

=sinsin

(4)

=cos≅1

(5)

则可定义目标在和方向(也即和方向)的角位置分别为

(6)

(7)

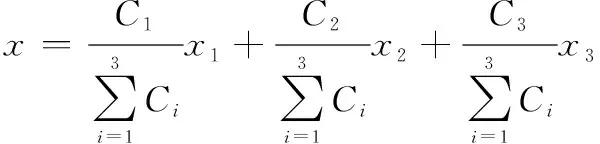
(8)

(9)

式中:(=1,2,3)为3个辐射单元的馈电系数,为实数。已假定各单元初始相位调整为同相。由重心公式,通过常规的矩阵求逆即得馈电系数关于单元位置和仿真点位置的表达:

(10)

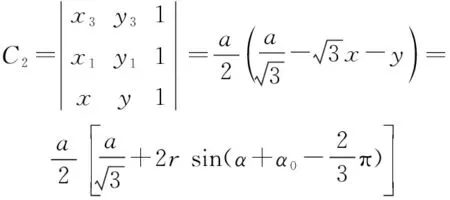
(11)

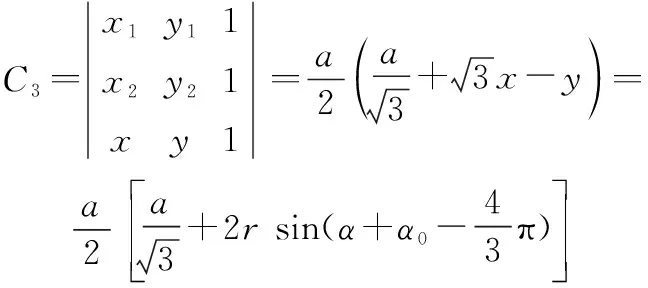
(12)

2 仿真误差的二维联合PDF

在进行半实物射频仿真时,由于器件性能和噪声的限制,各单元的馈电幅度不可能绝对精确,而是会存在一定误差,即、、存在误差。该幅度误差将会导致仿真给出的目标位置产生误差。若、、的误差记作Δ、Δ、Δ,则通过常规的偏微分运算可由式(8)得到方向上的仿真误差为

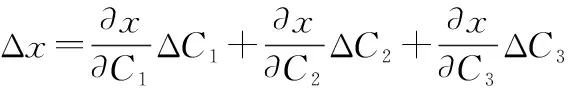
(13)

式中:

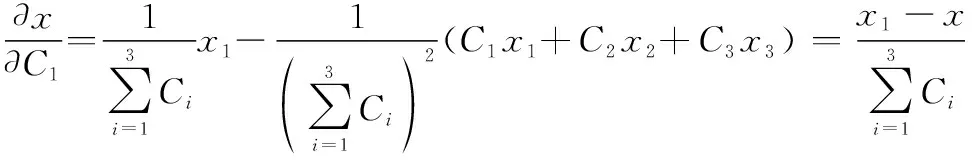
(14)

同理:

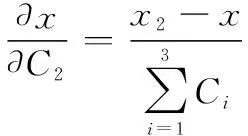
(15)

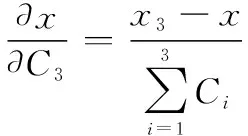
(16)

将式(14)～式(16)代入式(13),得

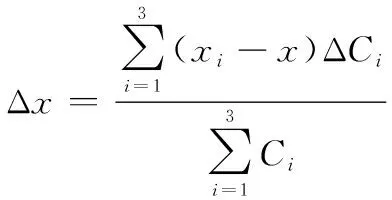
(17)

同理可得方向仿真误差为

(18)

由于Δ为馈电幅度误差随机变量,因而Δ和Δ也为误差随机变量，则ΔΔ的均值为

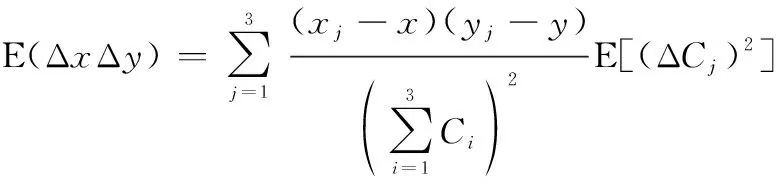
(19)

(20)

即

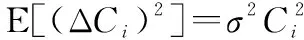
(21)

将式(21)代入式(19),得

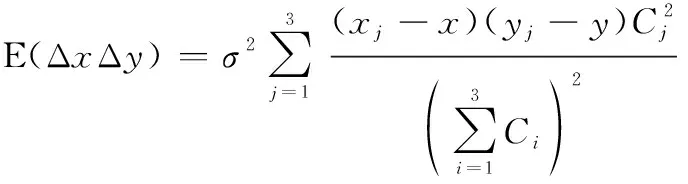
(22)

另外,和方向上的仿真角度误差方差为

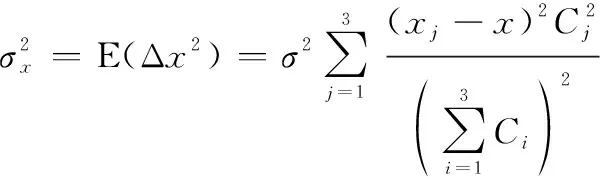
(23)

(24)

则可由式(22)～式(24)得Δ和Δ的相关系数为

(25)

从而Δ和Δ的联合PDF可以表示为

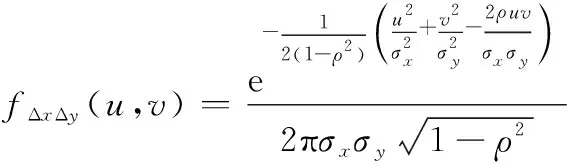
(26)

二维联合PDF的对称轴相对于轴的偏移角为

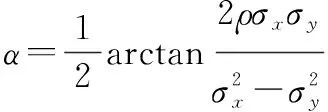
(27)

这表明,相关性的存在将会导致二维PDF的分布产生倾斜。

可以用长短轴之比

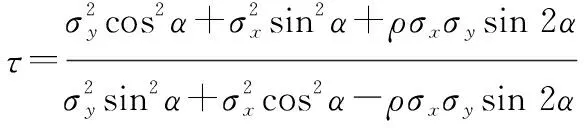
(28)

来表达仿真角度误差在方向上差异性的大小,以定量评估在航迹方向以及垂直航迹方向的角度误差之比的极值。

3 相关性与方差分析

首先讨论一个特殊的待仿真点目标位置,即点目标处于三元组三角形中心的情况。此时==0,代入式(25)得

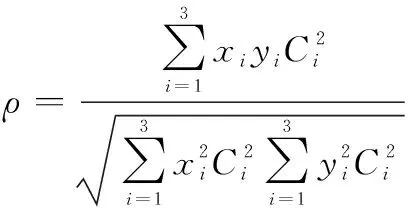
(29)

对于中心点目标,由于==,则式(29)可进一步化简为

(30)

将图1中给出的三元组各单元坐标代入可得=0。这表明,中心点处的仿真角度误差在和两个方向上不存在相关性。事实上,不论对图1所示坐标系如何旋转和平移,该结论都是成立的。这可由式(25)出发来获得证明。由于(,)为三元组的中心点,因而可以记:

(31)

(32)

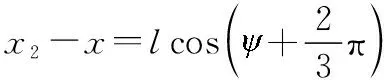
(33)

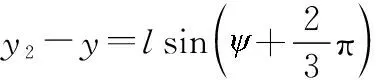
(34)

(35)

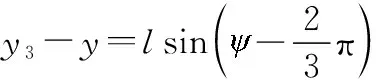
(36)

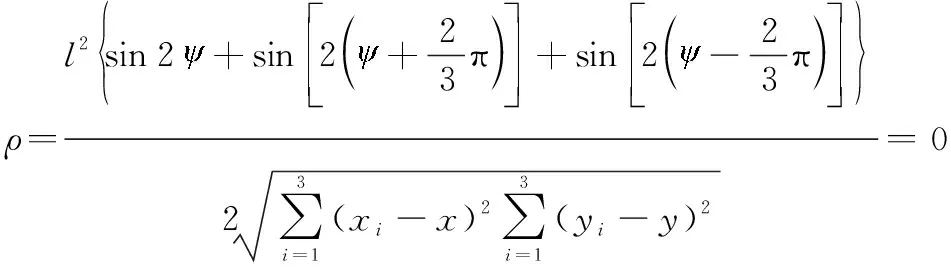
(37)

另外,可将式(31)～式(36)以及==代入式(23)和式(24),得

(38)

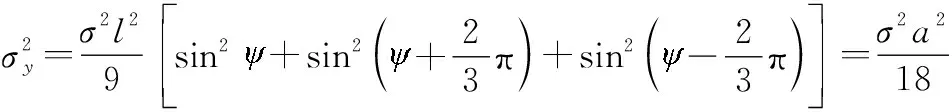
(39)

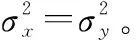
因而,在三元组中心点处,任意两个正交方向上的仿真角度误差皆不相关,且方差相等。

下面再对三元组内部对称轴上的点目标仿真角度误差进行分析。若点目标处于过单元1的对称轴(轴)上,则此时==0,-=-(-),-=-,=,代入式(23)～式(25),得

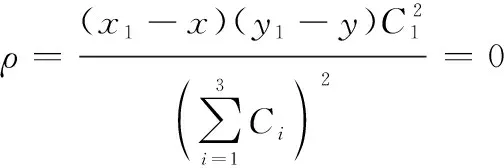
(40)

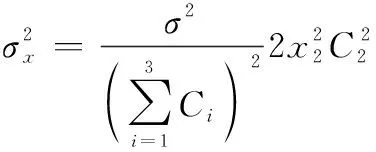
(41)

(42)

若点目标处于过单元2或单元3的对称轴上,则此时=或=,代入式(25),可知一般不为零。

以上为三元组内部点目标的仿真角度误差情况。对于处于三元组3条边上的点目标,其仿真角度误差PDF分布将退化成一维的情况。此时,仿真角度误差的PDF为沿着点目标所在三元组的边的分布函数,即联合PDF由面分布退化成了线分布。此时,由于仿真角度误差沿着一条确定的直线分布,因而Δ和Δ之间存在一个确定的线性关系。记:

Δ=Δ

(43)

4 数值结果

下面对上述解析分析结果作数值仿真计算。仿真所用坐标系亦如图1所示。三元组边长张角为=36 mrad,幅度相对误差的均方根为=002。针对(,)取值依次为(0003,0001 7)、(-0003,0001 7)、(0,-0003 5)、(0,0006 9)、(-0006,-0003 5)、(0006,-0003 5)、(0006,0003 5)、(-0006,0003 5)、(0,-0006 9)、(0,0013 9)、(-0012,-0006 9)、(0012,-0006 9)的12个待仿真点目标位置进行二维仿真角度误差联合PDF计算。这12个位置如图2所示。这12个位置实际上处于尺寸为三元组1/3和2/3的两个正三角形上,且处于三元组的3个对称轴上。图3给出了第8个位置处仿真角度误差的联合PDF三维图。可以看到,联合PDF的对称轴相对于轴产生了倾斜。为了更好地观察仿真误差联合PDF的分布,图4给出了等值线图。图4(a)～图4(l)分别依次给出了目标所在位置为第1～12处的仿真误差联合PDF的等值线分布。可以看到,位置1、2、5、6、7、8、11、12处的PDF产生了倾斜,其等概率密度线椭圆的对称轴偏离了轴;而位置3、4、9、10处并没有产生倾斜。注意到,位置3、4、9、10正处于三元组的对称轴轴上,而此处相关系数为零。另外,2、5、8、11向着同一侧倾斜,1、6、7、12向着同一侧倾斜。这是因为轴右侧的区域相关系数为负,而左侧区域的相关系数为正。对比1、2、5、6和7、8、11、12可以看到,越偏离轴,椭圆越扁。

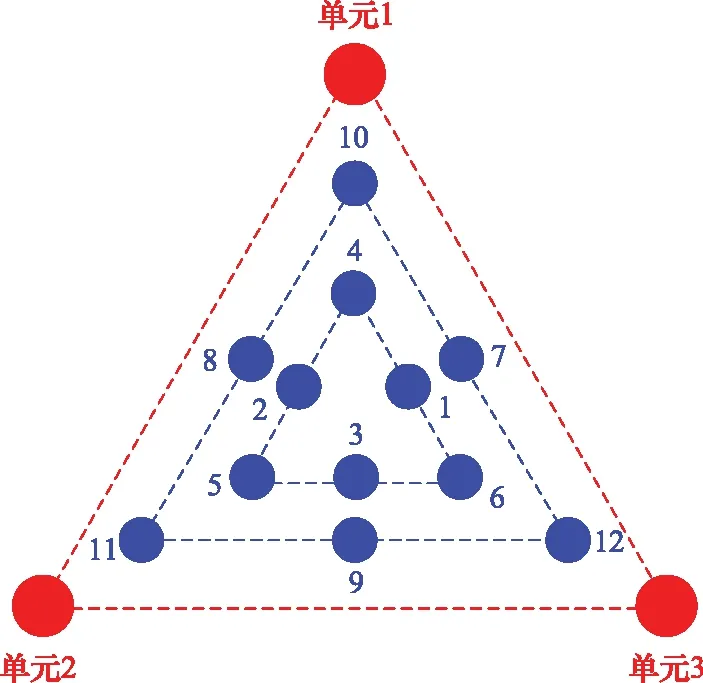
图2 仿真目标位置示意图Fig.2 Locations schematic diagram of the simulated targets

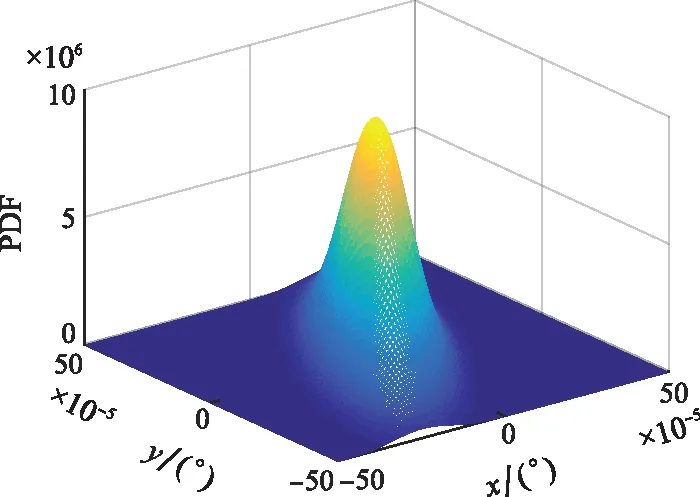
图3 目标位置8处仿真误差PDFFig.3 PDF of simulation error at location 8

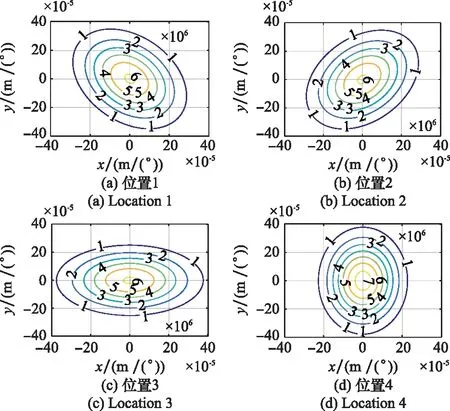
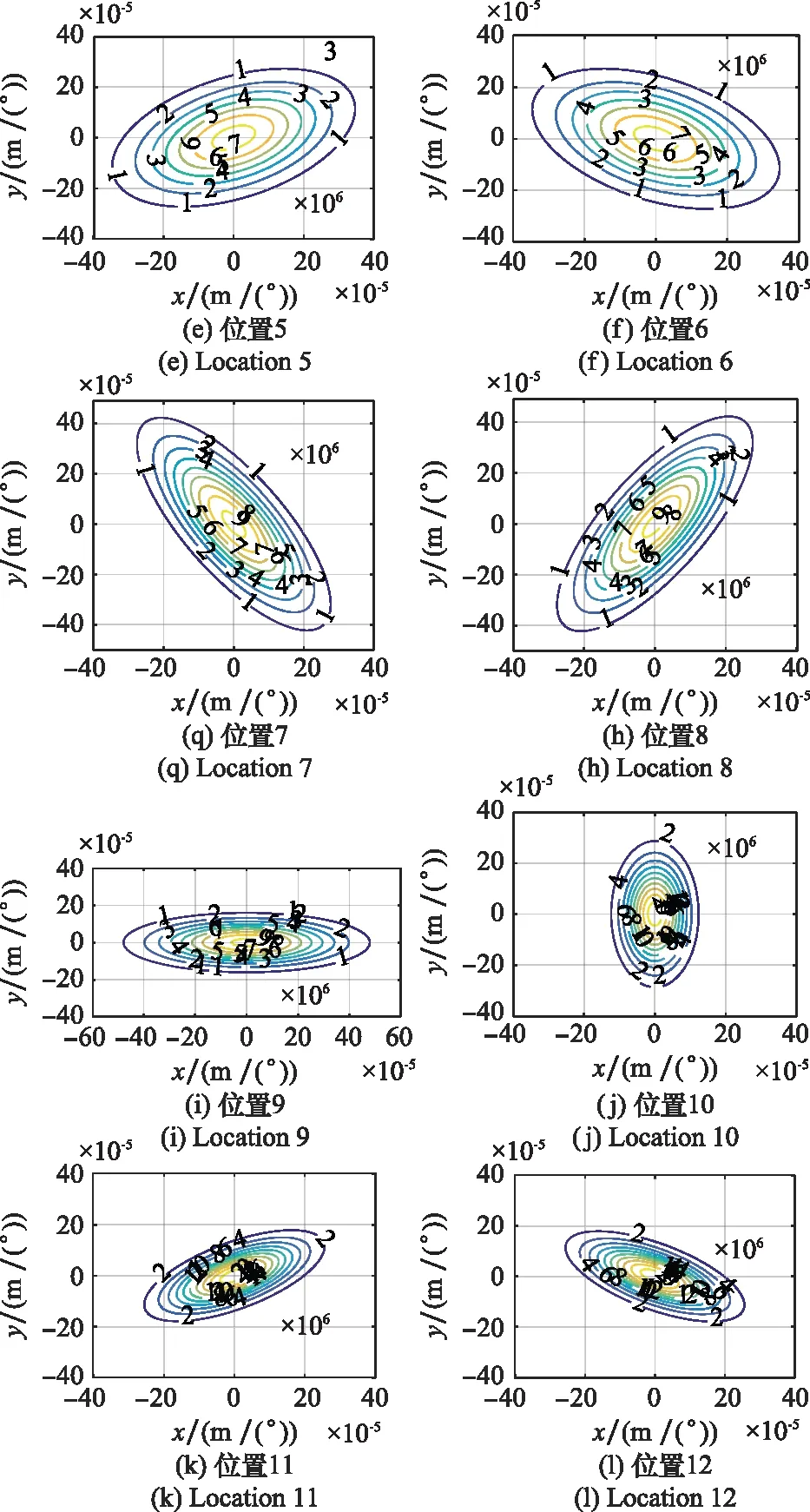
图4 二维误差联合PDF分布图Fig.4 Two-dimensional error joint PDF distribution

虽然在推导误差二维分布函数的过程中设立了具体的坐标系,然而在幅度重心公式的研究框架下,误差二维分布函数在三元组中的分布图与坐标系的选择无关。仔细观察图4,这12个点的误差分布图正如其在三元组中的位置一样,具有120°的旋转对称性,这与坐标系的选择无关。

为了更全面地考察整个三元组内部各点处的仿真误差PDF的特点,图5给出了三元组内部各点处的和两个方向上的仿真角度误差的相关系数分布。图5(a)给出了三维图,图5(b)给出了等值线图。由图5可以看到,相关系数在轴上为零,由轴向两侧的两条边,相关性逐渐增大。向右侧边是负相关增强,向左侧边是正相关增强。相关系数的分布是随坐标系的选取而变化的,因而此处结果仅针对本文坐标系。

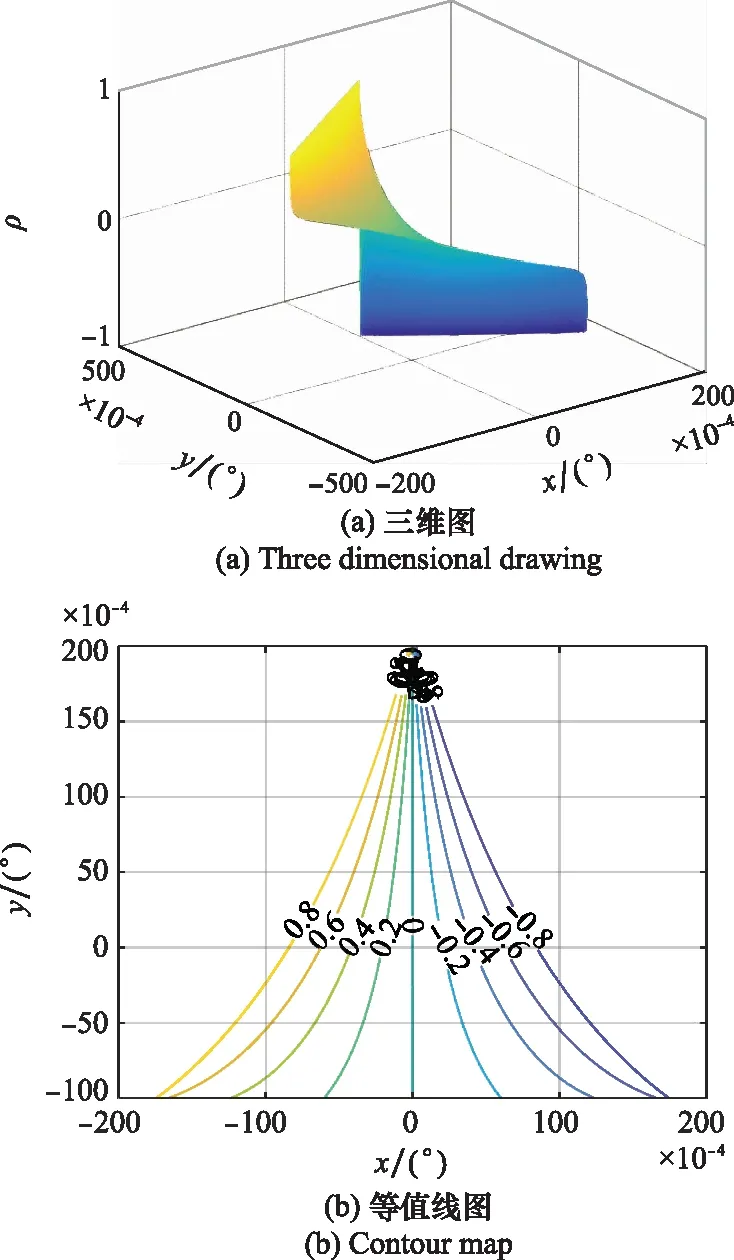
图5 相关系数分布Fig.5 Correlation coefficient distribution

5 结 论

本文通过解析分析和数值计算,给出了半实物射频仿真的仿真角度误差的联合概率密度分布。在三元组的3条中线上误差椭圆的长短轴分别平行于三元组的中线与其对应边。三元组外,在三元组中线延长线上的误差椭圆分布也有相同的规律。通过对其有关参数——相关系数和方差进行研究,给出了其分布特点。在三元组中心点处,任意两个正交的方向上其仿真角度误差不相关,且任意两个正交方向上的误差方差相等,其联合PDF的等值线分布图是一系列的同心圆。当某个坐标轴为三元组的某个对称轴而另一坐标轴与三元组一边平行时,在该对称轴上的各点处,两个坐标方向上的仿真角度误差不相关。且由该对称轴分别向两侧,即两个坐标方向上的仿真角度误差的相关性越来越强。在该对称轴的两侧,联合PDF的等值线椭圆产生倾斜,且离开该对称轴越远,椭圆越扁,直到在左右两个侧边上收缩成一条线。